無錫碩放機場進近航空器復飛階段碰撞風險評估
王勇 孫英然


摘?要:為評估無錫碩放機場雷達管制下進近航空器復飛階段的碰撞風險,采用概率論模型,分別計算航空器側向、縱向和垂直間的碰撞風險,從而確定總碰撞風險。經計算,無錫碩放機場進近雷達管制間隔18千米時以及縮小到10千米時,復飛階段航空器的碰撞風險均滿足安全目標水平。
關鍵詞:碰撞風險;安全評估;復飛階段
無錫地區經濟發展迅速,促進了無錫碩放機場飛行量日益增加,自2020年12月31號無錫機場實施雷達管制至今,無錫機場雷達運行安全裕度較高、風險系數較低、目前的雷達間隔較大,為進一步增加空中流量,從航空器碰撞風險角度考慮,評估目前雷達管制間隔下進近航空器的碰撞風險,并嘗試縮小間隔,以提高航空器在無錫碩放機場進近的運行效率。
在國外對航空器碰撞風險的研究,最早是英國的P.G.Reich提出一種碰撞風險模型,他分別從航空器的橫向、縱向和垂直方向計算航路上的航空器間的碰撞風險,提供了一種確定航路間隔和評估航路系統安全等級的方法,為后續對航空器碰撞風險和間隔確定的研究奠定基礎[13]。后來有學者開始研究航空器在進近過程中的碰撞風險,Domino?D?A等,通過實驗模擬,分析了航空器進近時,采用駕駛員自主保持間隔的方法,航空器之間的碰撞風險[4];Madden?M?M通過研究航空器進近時,速度和位置的變化軌跡,對其進近過程中前后距離變化做了詳細的分析,從而計算出碰撞風險[5];Guerreiro?N等考慮了尾流的影響,分析其數據特征,建立了考慮尾流間隔的碰撞風險模型[6]。
在國內,張兆寧等在著作《飛行間隔安全評估引論》中,介紹了飛行間隔安全評估基本概念,并從安全目標水平的確定、RECIH改進模型及應用、基于時間的碰撞風險模型及應用、基于沖突區域和位置誤差的概率模型及應用、最小安全間隔計算方法和基于CNS性能的安全評估模型,建立了飛行間隔安全評估理論體系[7];韓松臣等人考慮了在航路交叉點附近的航空器的標稱位置的變化情況,認為在此處航空器的碰撞風險較大,所以引入時間間隔變量,計算了航空器在航路交叉點上的碰撞風險[8];盧飛等分別研究了航空器近距平行跑道配對進近時航空器間的縱向、側向碰撞風險評估[910];張兆寧等人采用了基于事件概率思想建立碰撞風險模型,評估側向跑道雷達間隔進場和離場時的碰撞風險[11];岳睿媛等提出使用改進的Event模型對航路上飛行的航空器垂直方向上的碰撞風險進行評估[12]。
對于無錫碩放機場進近航空器之間的碰撞風險評估,分為兩個航空器同時進近時的碰撞風險、前機起飛后機進近時的碰撞風險和前機復飛后機進近時的碰撞風險。由于國內外針對航空器復飛階段的碰撞風險評估研究不足,所以本文主要研究航空器在復飛階段,即前機復飛、后機進近時的碰撞風險,為進一步縮小管制間隔提供依據。
1?航空器復飛階段碰撞風險評估模型
1.1?航空器復飛階段碰撞風險情況說明
在航空器進近過程中,如果無法保證安全著陸,就要執行復飛程序,當前機執行復飛程序時,與緊跟其后的正在進近的航空器之間存在碰撞風險。結合無錫碩放機場現狀,可將復飛階段的碰撞風險分為兩種情況,如圖1和圖2。
圖1中表示航空器A1使用03號跑道的進近程序進行進近,航空器B1使用03號跑道的復飛程序進行復飛,A1和B1之間存在碰撞風險;圖2中表示航空器A2使用21號跑道的進近程序進行進近,航空器B2使用21號跑道的復飛程序進行復飛,A2和B2之間存在碰撞風險。
1.2?航空器碰撞風險模型
首先,計算兩航空器縱向的碰撞風險,航空器i在t時刻縱向位置誤差服從正態分布:
fix(t)~N(μix,σ2ix)(1)
設t時刻,航空器i距離基準航跡線上的基準點的縱向距離為dix(t),則此時航空器i的實際位置為:
Xi(t)=dix(t)+fix(t)(2)
由式(1)和式(2)得前后兩架航空器在t時刻的實際縱向間隔為:
X1(t)X2(t)=(d1x(t)+f1x(t))-(d2x(t)+f2x(t))(3)
分解式(3)可得:
X1(t)X2(t)=(d1x(t)-(d2x(t))+(f1x(t)-f2x(t))(4)
其中令d1x(t)-d2x(t)=Lx(t),Lx(t)符合航空器進近時的運動學方程,且由式(1)得f1x(t)-f2x(t)~N(μ1xμ2x,σ21x+σ22x),則根據概率論計算兩航空器t時刻縱向碰撞風險為:
PX(t)=12π(σ21x+σ22x)λxλxexp[(x(Lx(t)+μ1x-μ2x))22(σ21x+σ22x)]dx(5)
然后,同理得兩航空器在側向和垂直方向的碰撞風險為:
PY(t)=12π(σ21y+σ22y)λyλyexp[(x(Ly(t)+μ1y-μ2y))22(σ21y+σ22y)]dx(6)
PZ(t)=12π(σ21z+σ22z)λzλzexp[(x(Lz(t)+μ1z-μ2z))22(σ21z+σ22z)]dx(7)
最后,兩航空器在t時刻,總碰撞風險概率為三個方向碰撞風險之積:
P=PX(t)×PY(t)×PZ(t)(8)
2?航空器碰撞風險評估參數
2.1?機型參數分析
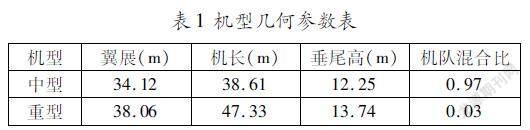
根據航空器碰撞風險模型,計算碰撞風險時需要的機型參數是航空器的機身長λx、翼展λy和垂尾高λz。在計算時如果考慮飛機的具體機型,雖然符合實際情況,但是會增加模型的復雜程度,并且由于機場運行的飛機機型種類較多,考慮具體機型會導致計算量急劇增大,因此對機型做一般處理。考慮整體情況,將機型參數按照各機型的機隊混合比進行加權平均,在計算過程中,所有的機型參數使用加權平均的結果。
設機型i的機隊混合比為pi,機型參數為λi,j(j=x,y,z,x表示機身長,y表示翼展,z表示垂尾高),則機型幾何參數可以表示為:
λi=∑iλi,jpi(9)
2.2?航空器位置誤差參數分析
航空器位置誤差表示為航空器偏離參考基準線的距離,對于采用標準進離場程序的航空器,參考基準線為相應的進離場程序,本文評估的是航空器復飛階段的碰撞風險,所以僅考慮最后進近階段,此階段的參考基準線利用最后進近定位點即FAF點和跑道入口點的經緯度坐標計算,采用參數方程的形式給出。
設連接跑道入口點與FAF點的直線段方程如下:
y-y1x-x1=y1F-y1x1F-x1(10)
其中x1F
y1F表示直線段上給定點的緯度。化簡為點斜式:
y=kx+b(11)
其中k=y1F-y1x1F-x1,b=y1-kx1。
給定航跡點P'=(x',y'),假設直線段上離P'最近的點為P=(x,y),那么(x,y)可以根據如下公式進行計算:
x=x'+k(y'-b)k2+1
y=b+kx'+k2y'k2+1(12)
進而我們可以利用余弦定理計算P'到P的球面距離,也即P'的近似位置誤差:
L=arccos(cos(90-y)cos(90-y')+sin(90-y)sin(90-y')cos(y-y'))180*π*R(13)
航空器運行過程中的位置誤差分為縱向位置誤差、側向位置誤差和垂直位置誤差。
2.2.1?縱向位置誤差
飛機在縱向的位置誤差主要是由于飛機速度誤差造成的,具體計算步驟如下:
Step1:計算n個航空器在進近階段各自速度的平均值;
Step2:把平均值當作預設值,把航空器每個時刻的速度值與平均值的偏差視為速度誤差;
Step3:計算進近時間段內以平均速度飛行的距離為均值μx,進近時間段乘以速度誤差得到均方差σx。
2.2.2?側向位置誤差
飛機在側向的位置誤差主要受導航精度誤差和飛行員操作誤差影響,反映在三維空間,表現為航空器偏離基準航跡的水平距離,具體計算步驟如下:
Step1:根據進近程序和復飛程序,確定基準航跡線BaseLine;
Step2:描繪n架航空器在進近階段的實際三維位置坐標(x,y,z);
Step3:計算n架航空器進近時實際位置與基準航跡線的水平距離為均方差σy。
2.2.3?垂直位置誤差
飛機在垂直的位置誤差主要受氣壓高度修正誤差、飛行員操作誤差影響,反映在三維空間,表現為航空器位置偏離基準航跡的垂直距離具體計算步驟如下:
Step1:根據進近程序和復飛程序,確定基準航跡線BaseLine;
Step2:描繪n架航空器在進近階段的實際三維位置坐標(x,y,z);
Step3:計算n架航空器進近時實際位置與基準航跡線的垂直距離為均方差σz。
3?航空器復飛階段碰撞風險評估結果
3.1?輸入參數
根據無錫碩放機場2021年5月5日至2021年5月7日的航班運行數據,將機型參數按照各機型的機隊混合比進行加權平均,得到中型機和重型機幾何參數如表1所示。
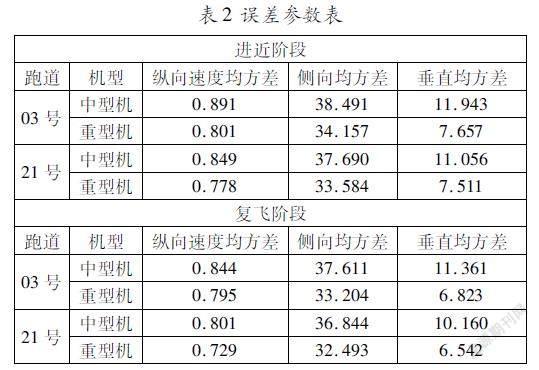
根據航空器位置誤差參數計算方法,得到航空器在進近階段和復飛階段,分別在03號跑道和21號跑道的縱向速度均方差、側向和垂直方向的位置誤差均方差,如表2所示。
3.2?碰撞風險計算結果
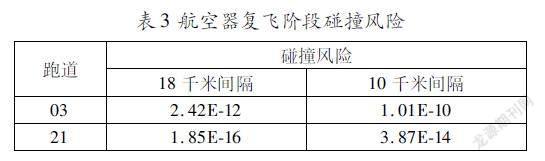
將機型參數和航空器進近和復飛時的誤差代入碰撞風險模型,計算當管制間隔分別為18千米和10千米時,使用03號跑道和21號跑道進近的航空器復飛階段的碰撞風險如表3。
在管制間隔為18千米和10千米時,當前機處于復飛階段、后機處于進近階段的航空器碰撞風險滿足1.0E7的安全目標水平。
結語
本文提出了航空器在復飛階段的碰撞風險評估模型,對無錫碩放機場進近的航空器進行碰撞風險評估,當航空器進近時的雷達管制間隔為18千米時,碰撞風險值較低,安全裕度較高;當管制間隔縮小到10千米時風險值仍滿足安全目標水平,故從復飛階段的航空器碰撞風險角度考慮,可以縮小管制間隔,為實現縮小無錫碩放機場進近雷達管制間隔提供理論依據。
參考文獻:
[1]Reich?P?G.Analysis?of?longrange?air?traffic?systems:Separation?standards?I[J].Journal?of?Navigation,1996,19(1):8889.
[2]Reich?P?G.Analysis?of?longrange?air?traffic?systems:Separation?standards?II[J].Journal?of?Navigation,1996,19(2):169186.
[3]Reich?P?G.Analysis?of?;longrange?air?traffic?systems:Separation?standards?III[J].Journal?of?Navigation,1996,19(3):331347.
[4]Domino?D?A,Tuomey?D,Mundra?A,et?al.Air?ground?collaboration?through?delegated?separation:Results?of?simulations?for?arrivals?to?closely?spaced?parallel?runways[C]//Integrated?Communications,Navigation?and?Surveilance?Conference(ICNS),2011.
[5]Madden?M?M.Kinematic?Modeling?of?Separation?Compression?for?Paired?Approaches?to?CloselySpaced?Parallel?Runways[C]//Aiaa?Aviation?Technology,Integration,&?Operations?Conference,2006.
[6]Guerreiro?N,Neitzke?K.Simulated?Wake?Characteristics?Data?for?Closely?Spaced?Parallel?Runway?Operations?Analysis[C]//Aiaa?Aviation?Technology,Integration,&?Operations,2013.
[7]張兆寧,王莉莉,李冬賓.飛行間隔安全評估引論[M].科學出版社,2009.
[8]韓松臣,曲玉玲,孫樊榮,朱新平.航路交叉點處碰撞風險模型[J].西南交通大學學報,2013,48(02):383389.
[9]盧飛,張兆寧,魏志強,劉碧蓮.近距平行跑道配對進近縱向碰撞風險安全評估[J].中國安全科學學報,2013,23(08):108113.
[10]盧飛,朱楠,楊斯,張兆寧,劉碧蓮.近距平行跑道配對進近側向碰撞風險評估[J].中國安全科學學報,2016,26(11):8792.
[11]張兆寧,徐超,盧婷婷.雷達間隔下的側向跑道運行碰撞風險[J].科學技術與工程,2019,19(25):386391.
[12]岳睿媛,蘇彬,朱新平,曹哲.基于改進Event模型的航路飛行過程垂直碰撞風險研究[J/OL].航空工程進展,20210816:16.
基金項目:中央高校基本科研業務費中國民航大學專項(3122017061)資助
作者簡介:王勇(1971—?),男,江蘇東海人,高級工程師,現為蘇南碩放國際機場有限公司航行保障部經理(兼書記);孫英然(1997—?),女,河北承德人,碩士,研究方向:空中交通運輸規劃與管理。

