一個整數分解和素性判別的新方法
李良元
(重慶航天職業技術學院,重慶 400021)
1 預備工作
整數分解和素性判別是數論中的重要課題,數論中很多問題都跟其有關,這個課題在密碼學中有極其重要的地位,但在實際計算中,我們還沒有簡易可行的方法去分解一個大整數或判斷哪些正整數是素數。隨著計算機運行速度的提升,互聯網的廣泛應用,在整數分解與素性判別方面取得了一些成果。由全球麥森(Mersenne)數愛好者參與的GIMPS(互聯網麥森素數大搜尋)項目,在2018年12月找到了第51個麥森(Mersenne)數,但最近三年也沒有找到新的麥森數。而第五個Fermat數之后是否還有Fermat素數依然是一個沒有解決的問題。有些Fermat數盡管我們知道它們是合數,也不知道如何分解。本文運用數論和代數的基本知識,給出了一種整數分解和素性判別的新方法,并可以有效運用于麥森數,費馬(Fermat)數的素性判別。
定義1設奇數m3。滿足同余式2T≡1(modm)的最小正整數T稱為2對模m的指數(本文簡稱為m的指數)。m的指數為T的素因數或指數為T的素因數的乘積叫做m的主因數。
引理 1([1])
設素數p的指數為T,則T|p-1.
引理 2([1])
設m的指數為T,其素數分解式為,pi的指數為Ti,則Ti|T.
定理 1設m的指數為T,素數p1,p2是其主因數,則p1p2≡ 1(modT).
證明:由于p1,p2是m的主因數,根據引理1,pi≡ 1(modT),i=1,2,因此,p1p2≡ 1(modT)。根據定理 1,立刻可得。
定理 2設m的指數為T,MT是其主因數,則MT≡ 1(modT)。為了后面計算中上界的設定,我們還需要下面的引理。
引理 3([2])
設mN,而m非素數,則m必為一不大于的素數所整除。
2 主因數的分解
設m的指數為T,MT為m的主因數,因此,

根據定理2,存在正整數h,使得MT=hT+1,并有非負整數a,b,0b 如果MT不是素數,設MI是MT的最小素因數,根據引理3, 且存在整數MIIMI,使得MT=MIMII。根據定義 1,MI,MII都是m的指數為T的主因數。由定理2,存在正整數x1,x2,使得 設k為待定非負整數,將(2.2)式化為 比較(2.5),(2.6)式,可知存在非負整數k,使x1x2=a-k,x1+x2=kT+b,即x1,x2為方程 的兩個正整數根,因此 因為x1,x2是正整數,根據(2.9),我們有q 這樣,對于每一組同時滿足(2.12)與(2.14)的k,q,由(2.5)都可以得到MT的一個分解: 當不存在整數k和q同時滿足(2.12)與(2.14)時,MT是素數。 形如2n-1的素數叫Mersenne數。設p是素數,Mp=2p-1,則 因此,Mp的指數為p.根據定義1與引理2,Mp的所有大于1的因數都是指數為p的主因數(根據定義1可知T2).利用上節的結果,我們可以對Mp進行素性判定. 例3.1判別M13的素性。 解:M13=213-1=8191=13×(48×13+6)+1,因此,a=48,b=6,T=13.由(2.12)式及(2.14)式, 由于沒有適合(3.2)式的整數q,k,因此,M13是素數.例3.2判別M29的素性。 解:M29=2291=536870911=29×(638372×29+2)+1,因此,a=638372,b=2,T=29.由(2.12)式及(2.14)式, 經過計算,(q,k)=(-14,2740),(-74,580),(-142,308)適合(3.3)式,因此,M29是合數。將此三組數據及a,b,T的值代入(2.5)式,們可以得到 M29=233×1103×2089. 另外,我們也可以利用后附的Table1-3判別Mersenne數的素性。 例3.3判別M11的素性。解:由Table 1知道,23的指數為11,因此,23|M11且23 形如22n+1的數叫Fermat數,記為Fn。由于 因此,Fn的指數為2n+1。根據定義1與引理2,Fn的所有大于1的因數都是指數為2n+1的主因數。利用第二節的結果,我們可以對Fn進行素性判定。由于 因此,在(2.2)式中, 此時,由(2.12)式及(2.14)式可得 記q=-2qF,由(4.3)式及(4.4)式可得 并由(2.15)得到 例4.1判別Fn,1n5的素性。 解:當n=1,2,3,4時,很容易算出沒有適合(4.5)式的整數qF,k,因此,Fn是素數.當n=5時,由(4.5)知, 計算可得qF=10,k=1636.由(4.6)可得 F5=(25+1·10+1)(25+1(25+·11636-10)+1)=641·6700417.我們知道,F14是合數,但我們目前還不知道其任何真因子。通過上面的例子,我們給出一個求其真因子的一個算法。 例4.2F14的分解。 解:由(4.5)知, 通過計算,找出滿足上式的qF和k,就可以由(4.6)得到F14的兩個真因子。 另外,我們也可以利用Table 1-3判別Mersenne數的素性。 例4.3判別F4的素性。 解:由于F4=216+1=65537,216≡-1(mod F4),因此,F4的指數是32,根據引理2,F4的素因數的指數都是32.但.由Table 3知道,沒有小于或等于256且指數為32的素數。根據引理3,F4是素數。 設m的指數為T,其素數分解式為,pi的指數為Ti,由引理2知道Ti|T。 對于整數m,我們先計算出指數T。根據引理2,m的素因子pi的指數都是T的因子,因此,我們先計算出T的所有大于1的因子Ti,再找出指數為Ti的素數qi,檢驗qi是否為m的因子就可以了。 例5.1分解整數m=4311744255。 解:容易算出,m的指數是48,其大于1的因子有2,3,4,6,8,12,16,24,48.根據計算可知(亦可在 Table 3中查找),指數為2的素數是3,指數為3的素數是7,指數為4的素數是5,沒有指數為6的素數,指數為8的素數是17,指數為12的素數是13,指數為16的素數是257,指數為24的素數是241,指數為48的素數是97和673.經驗算,3,5,7,13,17,241,257是m 的素因子,并得出分解式: 以上首先定義了主因子及其對應的主因數概念,其基本思路是一個“分”字,從而擺脫過去的“篩”字,并按指數分類列出了少部分素數,從中可探索出素數的分布規律。 其次給出了m3的奇數素性判別公式計算法,也可以變換為多項式計算法。 對于m3正奇整數的素因子分解可由同余式2T=1,mod(m)的T決定。根據T的真因子和主因子對應的素數,經驗算可得出m的素因子分解,做到完全指數分解法。

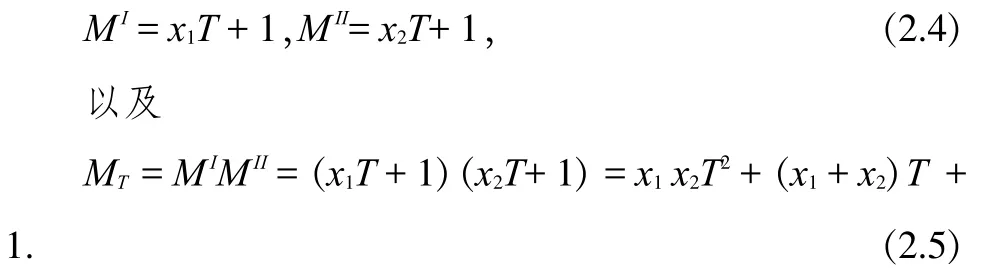
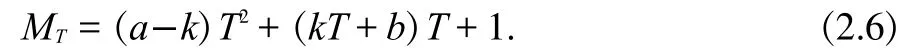
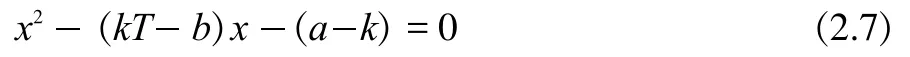

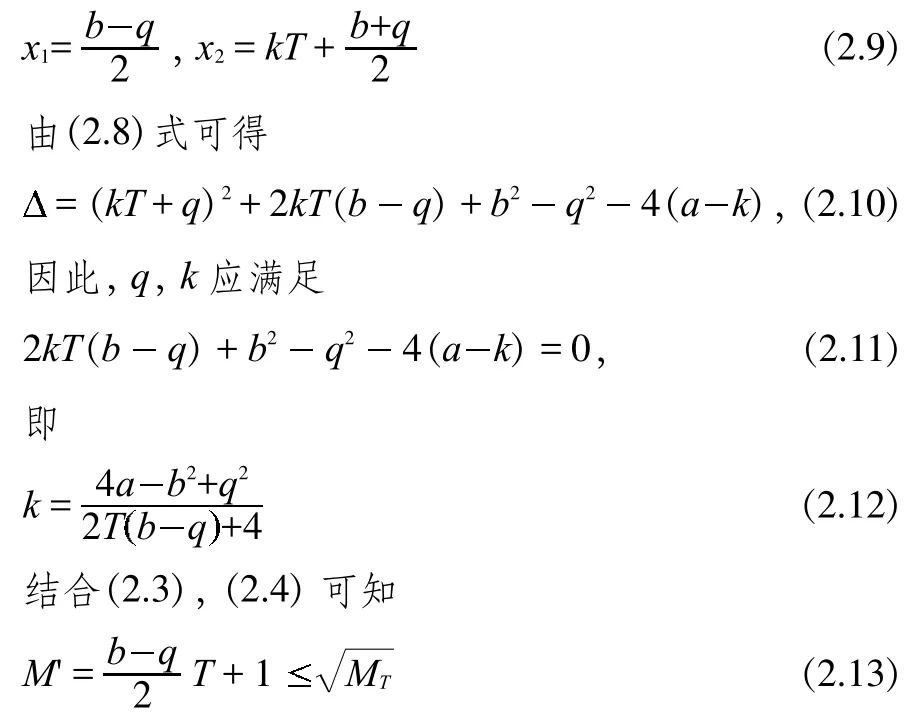
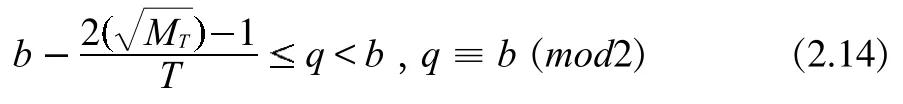
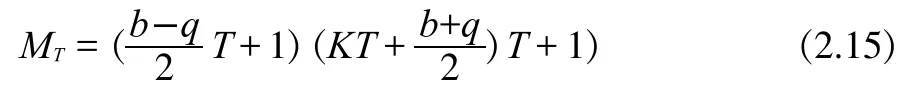
3 Mersenne數的素性判定

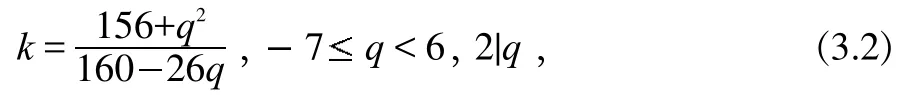
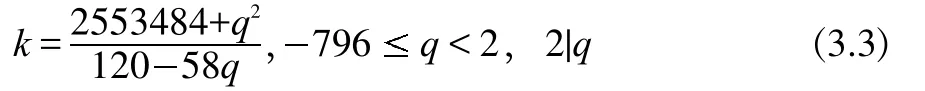
4 Fermat數的素性判定

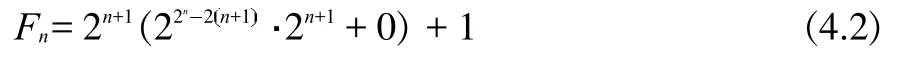



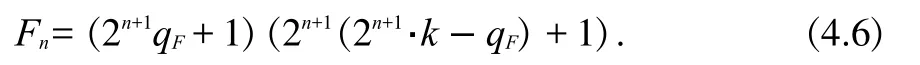
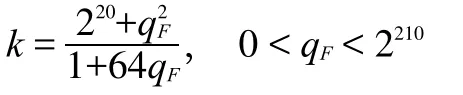

5 整數的素因子分解
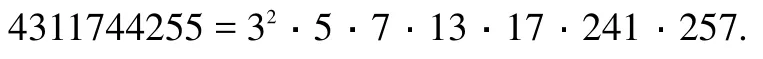
6 結語

