世界優(yōu)秀羽毛球男子單打前場(chǎng)技、戰(zhàn)術(shù)行動(dòng)與成績(jī)關(guān)系的研究

陳穗欽，郭智成

1 前言

已有的對(duì)世界優(yōu)秀羽毛球男子單打前場(chǎng)技－戰(zhàn)術(shù)研究中，有兩個(gè)顯著的結(jié)論：

1.1 在羽毛球前、中和后場(chǎng)，前場(chǎng)技、戰(zhàn)術(shù)運(yùn)用最多

有研究認(rèn)為，大約占到41%～43%之間（鐘建萍，2008；冷波，安忠鑫和周志輝，2013）；對(duì)世界排名前五選手的2008～2012年比賽技術(shù)統(tǒng)計(jì)中，前場(chǎng)技術(shù)使用占總拍數(shù)的33.24%（陳紅，2015）；2012年倫敦奧運(yùn)會(huì)林丹和李宗偉大戰(zhàn)中，林－李的前場(chǎng)球比例分別為51.44%和46.71%，都達(dá)到了40%以上的高占比（王德平，2013）；對(duì)李宗偉16場(chǎng)單打比賽研究表明，其前場(chǎng)技術(shù)使用率占41.6%（許坤，2016）。

1.2 前場(chǎng)不同技術(shù)使用率，從高到低排列次序

前場(chǎng)技術(shù)使用率從高到低依次是挑球、搓放球、推球、勾球（戴勁和鐘建萍，2009；孫志軍和賈洪祥，2014；陳天宇，2018）；湯姆斯杯和奧運(yùn)會(huì)中男子單打運(yùn)動(dòng)員，在前場(chǎng)進(jìn)攻技術(shù)運(yùn)用方面，運(yùn)動(dòng)員主動(dòng)進(jìn)攻技術(shù)較多，像推球技術(shù)，搓放網(wǎng)技術(shù)，但撲球技術(shù)的運(yùn)用較少（秦廣闊，2013）。

已有的研究揭示了前場(chǎng)技－戰(zhàn)術(shù)運(yùn)用的一些特征，如前場(chǎng)技－戰(zhàn)術(shù)運(yùn)用最多、各種技術(shù)使用頻率排列為挑－搓－推－勾球。研究中存在的主要問(wèn)題是：（1）多以個(gè)別的最優(yōu)秀的運(yùn)動(dòng)員為研究對(duì)象，采用頻數(shù)的統(tǒng)計(jì)方法分析數(shù)據(jù)，由于樣本量較小，及研究者的意識(shí)，沒(méi)有采用集中趨勢(shì)和離散趨勢(shì)來(lái)分析數(shù)據(jù)，因此研究雖為描述性研究，但研究的規(guī)范性限制了對(duì)特征的深入描述；（2）沒(méi)有進(jìn)一步探索羽毛球前場(chǎng)技－戰(zhàn)術(shù)運(yùn)用的因果關(guān)系，以及由此形成的深層次的機(jī)理和規(guī)律，可認(rèn)為這是制約競(jìng)技羽毛球運(yùn)動(dòng)發(fā)展的極為重要的原因之一。

2 結(jié)果與分析

美國(guó)《哈珀柯林斯社會(huì)學(xué)詞典》對(duì)理論的定義是：理論是“由邏輯的或數(shù)學(xué)的陳述所連接的一組假設(shè)或命題，它對(duì)經(jīng)驗(yàn)現(xiàn)實(shí)的某一領(lǐng)域或某一類現(xiàn)象提出解釋”；理論是“以一種系統(tǒng)化的方式將經(jīng)驗(yàn)世界中某些被挑選的方面概念化并組織起來(lái)的一組內(nèi)在相關(guān)的命題”。

2.1 勾球與成績(jī)關(guān)系的研究

勾球（網(wǎng)前勾對(duì)角球）是指把對(duì)方擊來(lái)的網(wǎng)前球，用屈腕（伸腕）的動(dòng)作，將對(duì)方來(lái)球回?fù)舻奖痉叫睂?duì)角、對(duì)方網(wǎng)前區(qū)域內(nèi)的一種擊球的技－戰(zhàn)術(shù)行動(dòng)。從擊球瞬間擊球點(diǎn)的高度進(jìn)行分類，勾球可分為網(wǎng)前高手／低手勾對(duì)角球兩種類型。

研究證明，球的“落點(diǎn)”和“線路”等是競(jìng)技羽毛球的制勝因素。因此，球的“落點(diǎn)”是擊球追求的重要目標(biāo)，因而是衡量網(wǎng)前勾對(duì)角球質(zhì)量的重要指標(biāo)。

假設(shè)運(yùn)動(dòng)員在p點(diǎn)勾球時(shí)，防守隊(duì)員處于d的位置（圖一），正常情況下，勾球“落點(diǎn)”會(huì)在對(duì)角網(wǎng)前相應(yīng)的“區(qū)域”（D1、D2、D3）。防守運(yùn)動(dòng)員“跑動(dòng)路線”（a1、a2、a3）路線距離分別是a1﹤a2﹤a3。當(dāng)落點(diǎn)在D3區(qū)域，防守運(yùn)動(dòng)員從中場(chǎng)d的位置、沿a3跑動(dòng)路線的距離最長(zhǎng)、所用的時(shí)間最多，所以從反應(yīng)→跑動(dòng)→回球的時(shí)間就越長(zhǎng)，由于行動(dòng)“倉(cāng)促”，回球方式選擇機(jī)會(huì)也會(huì)相對(duì)地較少，失誤的可能性會(huì)增大。因此，我們假設(shè)：“勾球的落點(diǎn)越偏，勾球直接得分就越多”。

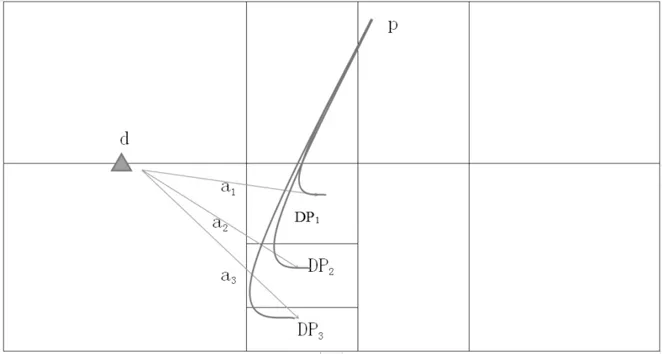
圖一 勾球落點(diǎn)和防守跑動(dòng)路線示意圖

統(tǒng)計(jì)結(jié)果表明（表1）：

（1）勾球落點(diǎn)次數(shù)（t）方面，運(yùn)動(dòng)員在D1t和D2t處落點(diǎn)的平均數(shù)3～4次之間，（t＝0.732，p＝0.497，p＞0.05），可認(rèn)為差異無(wú)統(tǒng)計(jì)學(xué)意義；D1t和D3t、D2t－D3t處落點(diǎn)之間平均數(shù)差異明顯，且達(dá)到顯著性水平（D1t－D3t，t＝－5.312，p＝0.003，p﹤0.05；D2t－D3t，t＝－3.675，p＝0.014，p﹤0.05）。

（2）勾球偏度得分（S2）方面，由于根據(jù)我們的判斷，距離中場(chǎng)站位越遠(yuǎn)、接球難度越大，因此，區(qū)域D1接球最易、區(qū)域D3接球最難，表1中D3t數(shù)據(jù)呈現(xiàn)出明顯的趨勢(shì)特點(diǎn)，直接支持我們這個(gè)觀點(diǎn)。正是基于該觀點(diǎn)，不同區(qū)域賦權(quán)后，區(qū)域D1s2－D2s2之間差異達(dá)不到顯著性水平（t＝－1.354，p＝0.234，p＜0.05）；而區(qū)域D1s2－D3s2（t＝－6.501，p＝0.001，p﹤0.05）和區(qū)域D2s2－D3s2（t＝－4.604，p＝0.006，p﹤0.05）差異達(dá)到非常顯著性水平。

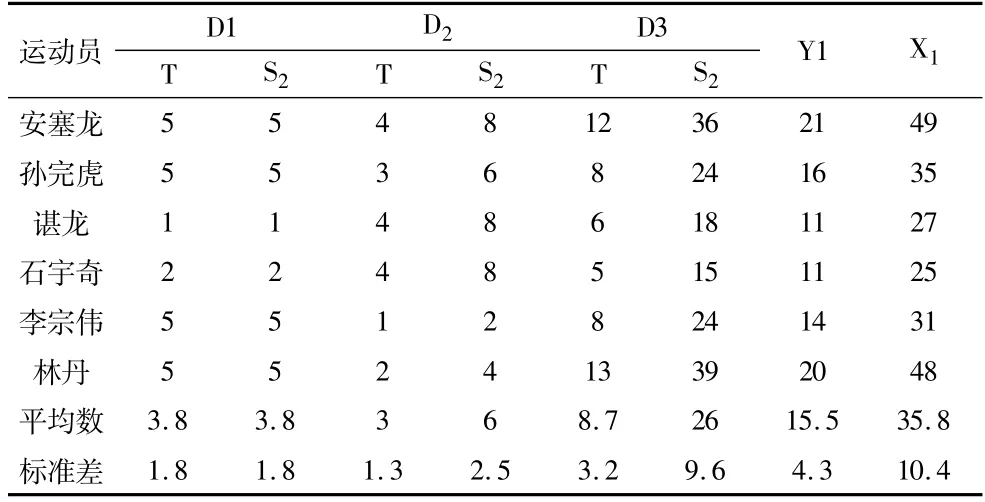
表1 運(yùn)動(dòng)員勾球落點(diǎn)及得分統(tǒng)計(jì)表

為了驗(yàn)證Y1（三個(gè)區(qū)域落點(diǎn)總次數(shù)）與X1（三個(gè)區(qū)域總偏度得分）之間的關(guān)系，本研究采用皮爾遜相關(guān)系數(shù)的方法進(jìn)行計(jì)算。為此，首先做出兩變量的散點(diǎn)圖，以判斷統(tǒng)計(jì)數(shù)據(jù)是否呈近似直線的關(guān)系，即檢驗(yàn)本研究變量數(shù)據(jù)是否達(dá)到使用皮爾遜相關(guān)系數(shù)統(tǒng)計(jì)方法的要求。由散點(diǎn)圖（圖二）可知，勾球得分與勾球距離偏度總得分呈近似直線關(guān)系，因此，可采用皮爾遜相關(guān)系數(shù)r計(jì)算兩變量的相關(guān)系數(shù)。

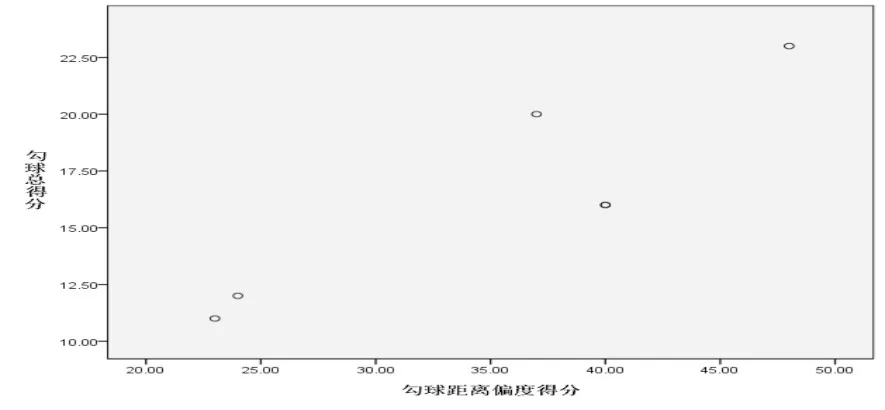
圖二 運(yùn)動(dòng)員偏度得分與得分散點(diǎn)圖

統(tǒng)計(jì)結(jié)果表明，Y1與X1之間達(dá)到高度相關(guān)（r＝.893，p＜0.05），證實(shí)“勾球的落點(diǎn)越偏，勾球直接得分就越多”的假設(shè)。

2.2 撲球與成績(jī)關(guān)系的研究

對(duì)方發(fā)網(wǎng)前球或回?fù)艟W(wǎng)前球時(shí)，在球剛越到網(wǎng)頂即迅速上網(wǎng)向斜下方撲壓，謂之撲球。撲球有正手撲球和反手撲球兩種。

從圖三來(lái)看，撲球落點(diǎn)D1在前場(chǎng)的區(qū)域內(nèi)，而撲球落點(diǎn)D2則在中場(chǎng)的區(qū)域內(nèi)，撲球落點(diǎn)DP3則在后場(chǎng)的區(qū)域內(nèi)。對(duì)于D1和D2落點(diǎn)的球防守隊(duì)員d一伸拍或上前一步即可接到球，但是落點(diǎn)D3的撲球在后場(chǎng)，撲球速度快，防守隊(duì)員d根本沒(méi)有足夠的時(shí)間后退和回?fù)羟颍虼朔朗仃?duì)員接住落點(diǎn)為D3的撲球的難度要比D1和D2的大。因此，我們假設(shè)：“進(jìn)攻方撲球搶點(diǎn)越高、落點(diǎn)越靠近后場(chǎng)（D3），撲球得分就越多”。

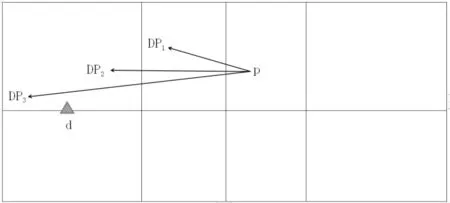
圖三 網(wǎng)前撲球區(qū)域和防守隊(duì)員站位示意圖

統(tǒng)計(jì)結(jié)果表明（表2）：

（1）撲球落點(diǎn)次數(shù)（t）方面，運(yùn)動(dòng)員在D1t和D2t處落點(diǎn)的平均數(shù)4～5次之間，（t＝0.338，p＝0.749，p＞0.05），D1t和D3t之間（D1t－D3t，t＝－1.465，p＝0.203，p＞0.05）可認(rèn)為差異無(wú)統(tǒng)計(jì)學(xué)意義；D2t－D3t處落點(diǎn)之間平均數(shù)差異明顯，且達(dá)到顯著性水平（D2t－D3t，t＝－2.3，p＝0.04，p﹤0.05）。

（2）撲球偏度得分（S2）方面，由于根據(jù)我們的判斷，撲球落點(diǎn)越靠近后場(chǎng)、球速越快、接球難度越大。因此，區(qū)域D1和D2接球最易、區(qū)域D3接球最難，表2中D3t數(shù)據(jù)呈現(xiàn)出明顯的趨勢(shì)特點(diǎn)，直接支持我們這個(gè)觀點(diǎn)。正是基于該觀點(diǎn)，不同區(qū)域賦權(quán)后，區(qū)域D1s2－D2s2之間差異達(dá)不到顯著性水平（t＝－0.937，p＝0.392，p＜0.05）；而區(qū)域D1s2－D3s2（t＝－5.035，p＝0.004，p﹤0.05）和區(qū)域D2s2－D3s2（t＝－3.642，p＝0.015，p﹤0.05）差異達(dá)到非常顯著性水平。

表2 運(yùn)動(dòng)員撲球落點(diǎn)及得分統(tǒng)計(jì)表

由散點(diǎn)圖（圖四）可知，撲球得分與撲球距離偏度總得分呈近似直線關(guān)系，因此，可采用皮爾遜相關(guān)系數(shù)r計(jì)算兩變量之間的相關(guān)系數(shù)。

圖四 運(yùn)動(dòng)員偏度得分與得分散點(diǎn)圖

相關(guān)分析表明（表3），撲球落點(diǎn)距離偏度總得分與撲球得分相關(guān)系數(shù)r＝.893（p＜0.05）。表明撲球得分與撲球落點(diǎn)距離偏度總得分呈高度正相關(guān)關(guān)系，證實(shí)“進(jìn)攻方撲球搶點(diǎn)越高、落點(diǎn)越靠近后場(chǎng)（D3），撲球得分就越多”。

表3 撲球得分與撲球距離偏度總得分相關(guān)系數(shù)

2.3 搓球與成績(jī)關(guān)系的研究

搓球是用球拍搓擊球的左側(cè)或右側(cè)下部與球托底部，使球向右側(cè)或左側(cè)旋轉(zhuǎn)與翻滾過(guò)網(wǎng)。搓球有正手搓球和反手搓球兩種。

從圖五中可以看出，當(dāng)搓球的落點(diǎn)在D3區(qū)域，防守運(yùn)動(dòng)員從中場(chǎng)跑動(dòng)到D3的距離最長(zhǎng)、所用的時(shí)間最多，所以從反應(yīng)→跑動(dòng)→接球→觸球→回球的時(shí)間就越長(zhǎng)，此種情況下回球方式也會(huì)相對(duì)地較少，處于被動(dòng)式回球方式，從而導(dǎo)致失誤率增高。因此，我們假設(shè)：“搓球的落點(diǎn)越偏，越靠近（D3），搓球的得分就越高”。

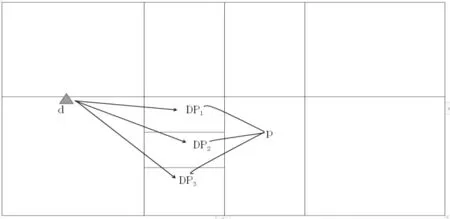
圖五 網(wǎng)前搓球球區(qū)域和防守隊(duì)員站位示意圖

統(tǒng)計(jì)結(jié)果表明（表4）：

（1）搓球落點(diǎn)次數(shù)（t）方面，運(yùn)動(dòng)員在D1t和D2t處落點(diǎn)的平均數(shù)2～3次之間，（t＝0.415，p＝0.695，p＞0.05），可認(rèn)為差異無(wú)統(tǒng)計(jì)學(xué)意義；D2t－D3t處落點(diǎn)之間平均數(shù)差異明顯，且達(dá)到顯著性水平（D1t－D3t，t＝－5.968，p＝0.002，p﹤0.05；D2t－D3t，t＝－5.428，p＝0.003，p﹤0.05）。

（2）搓球偏度得分（S2）方面，由于根據(jù)我們的判斷，搓球的落點(diǎn)越偏，越靠近（D3），回球難度越大。因此，區(qū)域D1回球最易、區(qū)域D2回球稍難，區(qū)域D3回球最難。表4中D3t數(shù)據(jù)呈現(xiàn)出明顯的趨勢(shì)特點(diǎn)，直接支持我們這個(gè)觀點(diǎn)。正是基于該觀點(diǎn)，不同區(qū)域賦權(quán)后，區(qū)域D1s2－D2s2之間差異達(dá)不到顯著性水平（t＝－0.933，p＝0.394，p＜0.05）；而區(qū)域D1s2－D3s2（t＝－6.301，p＝0.001，p﹤0.05）和區(qū)域D2s2－D3s2（t＝－5.827，p＝0.002，p﹤0.05）差異達(dá)到非常顯著性水平。

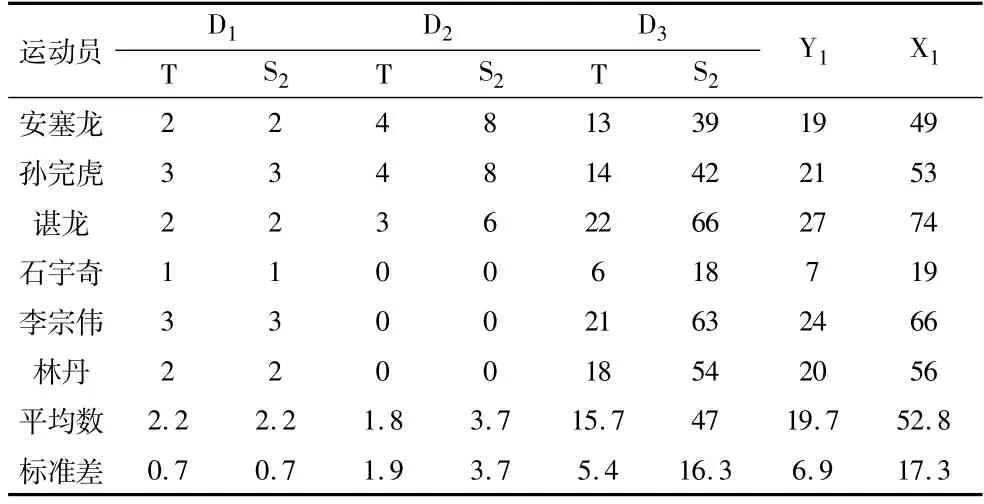
表4 運(yùn)動(dòng)員搓球落點(diǎn)及得分統(tǒng)計(jì)表

由散點(diǎn)圖（圖六）可知，搓球得分與搓球距離偏度總得分呈近似直線關(guān)系，因此，可采用皮爾遜相關(guān)系數(shù)r計(jì)算兩變量之間的相關(guān)系數(shù)。

圖六 運(yùn)動(dòng)員偏度得分與得分散點(diǎn)圖

相關(guān)分析表明（表5），搓球落點(diǎn)距離偏度總得分與搓球得分相關(guān)系數(shù)r＝.993（p＜0.01），表明搓球得分與搓球落點(diǎn)距離偏度總得分呈高度正相關(guān)關(guān)系，證實(shí)“搓球的落點(diǎn)越偏，越靠近（D3），搓球的得分就越高”。

表5 搓球得分與推球距離偏度總得分相關(guān)系數(shù)

3 結(jié)論

1.在30場(chǎng)71局的比賽中，針對(duì)運(yùn)動(dòng)員前場(chǎng)技戰(zhàn)術(shù)行動(dòng)進(jìn)行分析，前場(chǎng)技術(shù)使用率從高到低依次是挑球、搓放球、推球、勾球、撲球。但是其中挑球和推球都屬于防守類型的技戰(zhàn)術(shù)，不是主要的得分手段。所以本文著重研究前場(chǎng)搓球、勾球、撲球等技戰(zhàn)術(shù)行動(dòng)對(duì)于成績(jī)關(guān)系的研究。

2.對(duì)世界優(yōu)秀羽毛球男子前場(chǎng)單打技－戰(zhàn)術(shù)行動(dòng)與成績(jī)關(guān)系的觀察統(tǒng)計(jì)與皮爾遜相關(guān)系數(shù)計(jì)算分析，以及配對(duì)樣本T檢驗(yàn)的統(tǒng)計(jì)方法進(jìn)行驗(yàn)證，證實(shí)了以下假設(shè)是成立的：

（1）證實(shí)了“勾球的落點(diǎn)越偏，勾球直接得分就越多”。

（2）證實(shí)了“搓球的落點(diǎn)越偏，越靠近（DP3），搓球的得分就越高”

（3）證實(shí)了“進(jìn)攻方撲球搶點(diǎn)越高、落點(diǎn)越靠近后場(chǎng)（DP3），撲球得分就越多”。