動態超表面天線陣列混合發射波束成形

陳玉香, 陳勝垚, 冉龍瑤, 席 峰

(南京理工大學電子工程與光電技術學院, 江蘇 南京 210094)

0 引 言

動態超表面天線(dynamic metasurface antenna, DMA)是近年來基于超材料發展的一種新型陣列天線。與傳統微帶線饋電陣列天線相比,該天線將多個超材料陣元集成在一個天線上,并且共同使用一個波導作為饋源,使得天線結構更加緊湊,縮小天線尺寸可以很好地滿足復雜系統和多任務的工作需求。得益于超材料對電磁波的特殊調控能力,與常規相控陣天線相比,DMA不需要移相器、放大器等組件,而是通過調控每個陣元的極化度來產生幅度和相位因子,從而控制波束,大大提高了傳統天線的性能指標,如提高輻射增益、改善阻抗帶寬等。基于以上諸多優點,DMA目前被廣泛應用于近場計算成像、合成孔徑成像、衛星通信、5G移動通信等諸多領域。

隨著新一代信息通信技術和雷達應用的發展,毫米波頻段被用于緩解數據傳輸容量與頻譜短缺之間的矛盾。然而,與傳統頻段相比,毫米波信號在傳輸中散射更高、穿透損耗更大、衍射更低、路徑損耗更高,因此需要在特定角度形成波束,產生增益來彌補損耗。數字大規模陣列可以提供理想的波束形成權值,但是完全數字架構要求為每根天線配備獨立的射頻(radio frequency, RF)鏈路,這導致系統的功耗和成本顯著增加。模擬-數字混合陣列結構相對于全數字陣列結構而言,波束形成性能有所下降,但是所需的RF鏈路數量遠小于天線個數,顯著降低了系統的實現復雜度,目前已成為大規模多輸入多輸出(multiple input multiple output,MIMO)系統中的主流技術。模擬-數字混合波束成形(hybrid beamforming, HB)由低維度的基帶數字波束成形和高維度的RF模擬波束成形兩部分組成。在這種混合結構中,每條RF鏈路可同時連接多根天線,其中每根天線的信號相位受到模擬相位偏移網絡控制,可以產生不同的相移,這相當于對連接同一RF鏈路的多根天線進行了模擬波束成形處理。

目前,學者們在發射和接收端對模擬-數字HB技術均開展了諸多研究,本文主要關注發射端的HB。在大規模MIMO通信領域,發射波束成形通常稱為預編碼。文獻[9]研究混合預編碼對傳輸數據均方誤差的影響,提出了一種低復雜度的最小間隙迭代量化方法,將混合預編碼性能逼近于最優全數字預編碼。文獻[10]研究毫米波MIMO通信中如何優化混合預編碼以最大化頻譜效率,該文將混合預編碼轉化為矩陣分解問題,利用交替優化方法分別求解模擬和數字預編碼子矩陣。文獻[11]研究DMA的收發模型和波束成形能力,以探討其在6G通信各場景中應用的可能性。在毫米波MIMO雷達領域,文獻[12]研究發射HB和天線選擇聯合設計,利用softmax神經網絡進行天線選擇和波束成形權值優化,使得合成的波束圖與期望波束圖誤差最小。在雙功能雷達-通信(dual functional radar communication, DFRC)系統領域,文獻[13]研究用于毫米波DFRC系統的發射HB方法,以便在多用戶通信和雷達多目標檢測之間得到最優的折中性能,該文提出了一種交替優化方法,在給定發射功率的條件下,使得HB矩陣同時逼近于全數字最優通信發射權值矩陣與最優雷達發射權值矩陣。文獻[14]構建了一種毫米波DFRC系統工作模式,并提出了基站在不同工作階段采用的發射與接收HB方法,對于發射HB,該文采用交替優化技術設計模擬與數字權值矩陣,使得HB矩陣同時逼近于下鏈通信所需的迫零波束成形矩陣和雷達多目標跟蹤所需的多波束成形矩陣。

應當指出,上述HB研究均是基于唯相混合陣列開展的,基于DMA陣列的研究工作較少。由DMA的特性可知,基于DMA陣列的HB可以進一步簡化系統結構,降低系統的復雜度。為此,本文開展了基于DMA陣列的發射HB研究。不同于唯相混合陣列中模擬權值僅相位可調,DMA中模擬權值的幅度和相位均可調,只是二者之間存在耦合,因此DMA可能會提供更多的自由度。本文首先根據DMA的特征建立DMA陣列發射HB模型,然后利用交替優化思想提出一種基于交替方向乘子法(alternating direction multiplier method, ADMM)的模擬與數字權值聯合求解方法。該方法通過引入輔助變量簡化問題描述,然后通過交替優化求解輔助變量、數字權值和模擬權值。其中,輔助變量可獲得閉式解,數字權值和模擬權值則利用ADMM分別進行求解。仿真結果證實了所提方法的有效性和DMA陣列在發射HB方面的性能優勢。

1 問題模型

考慮由個一維DMA構成的一維均勻線性陣列,其中每個超表面天線由集成在一個波導上的個超材料陣元組成,如圖1所示。在每個DMA上,超材料陣元是均勻線性排列的,陣元間距為;個DMA則以間距均勻線性排列,其中=。一般而言,可以將每個超材料陣元等效為一個點偶極子。為了簡便分析,通常假設超材料陣元之間是弱耦合的,即可以忽略波導內陣元之間的耦合。

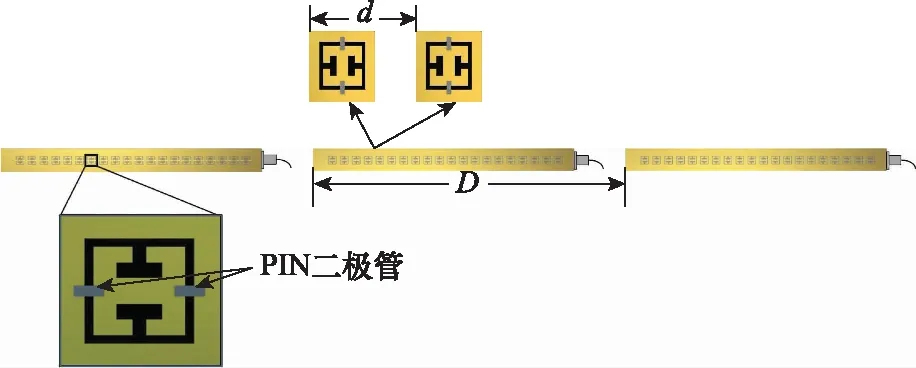
圖1 一維DMA組成的均勻線性陣列Fig.1 Uniform linear array composed of one-dimensional DMA

在一個DMA內,個超材料陣元在方向處形成的導向矢量為

()=[1,e-j( sin +),e-j( sin +)2,…,e-j( sin+)(-1)]∈×1

(1)

式中:=2π是自由空間的波數;()=2πc是沿波導的導波衰減率,表示波導指數,c表示光速。在中心頻率為的窄帶情況下,()近似為常數(),簡記為。組成陣列的個DMA在方向處的導向矢量為

()=[1,e-j sin ,e-j2 sin ,…,e-j(-1) sin ]∈×1

(2)

則整個DMA陣列的綜合導向矢量為

()=()?()∈×1

(3)

采用該DMA陣列進行發射波束成形,其等效模型如圖2所示。

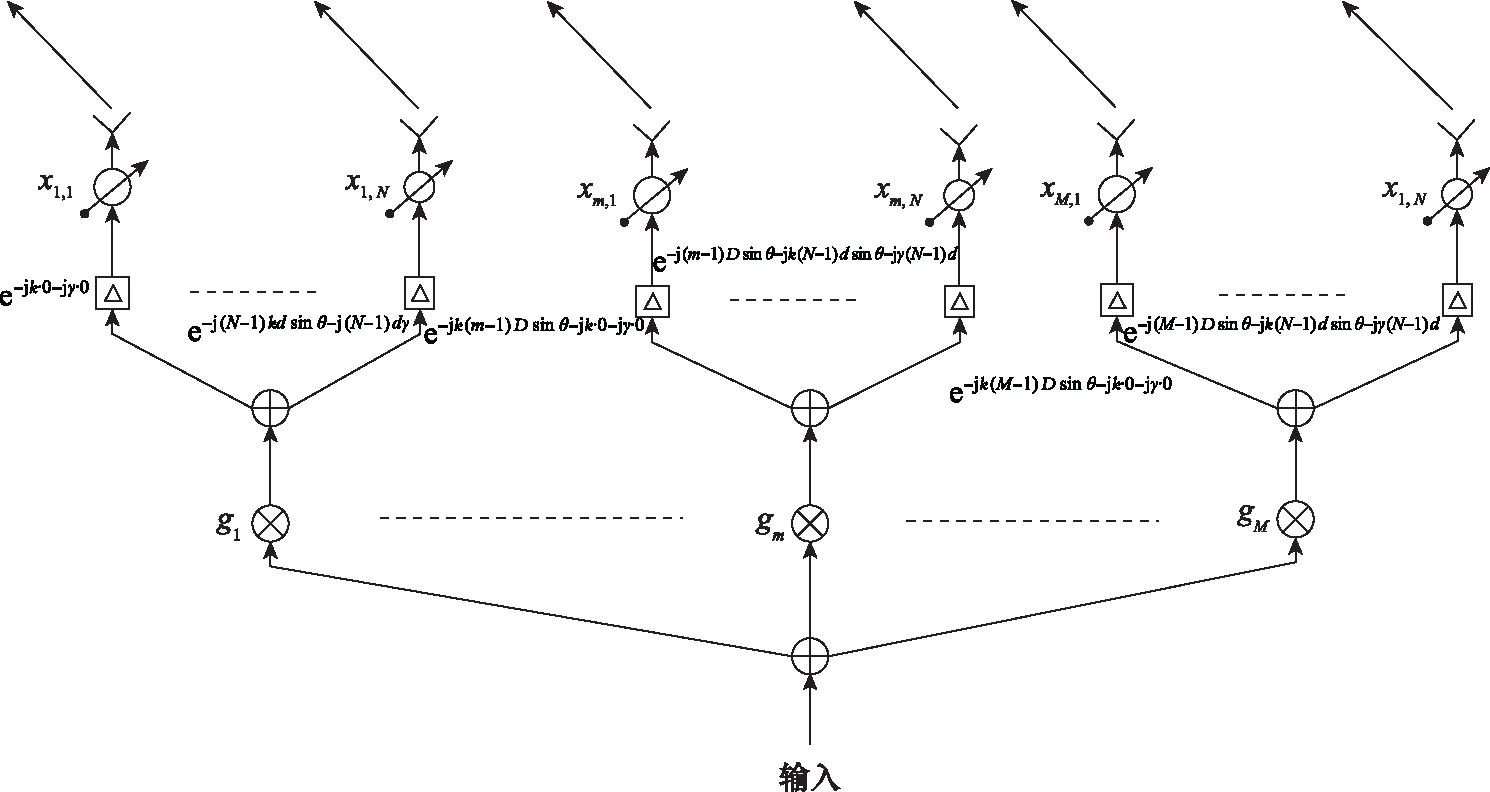
圖2 一維DMA陣列發射波束成形等效模型Fig.2 Equivalent model of one-dimensional DMA array transmit beamforming

其中,三角形符號描述每個超材料陣元在方向處產生的相移,可根據式(3)確定。定義第個DMA上第個陣元的模擬權值為,,其中=1,2,…,,=1,2,…,,則所有個超材料陣元的模擬權值組成的向量為

=[,,…,1,,…,,1,,,2,…,,]∈×1

(4)

與常規相控陣采用移相器實現模擬權值不同,DMA通過控制PIN二極管的工作狀態來調控模擬權值。因此,DMA模擬權值的幅度和相位均是可調的,只是二者之間存在一定的約束關系,不是獨立可調的。典型的DMA模擬權值約束形式有:唯幅度約束、二值幅度約束和洛倫茲相位約束。本文主要研究洛倫茲相位約束的情況,即模擬權值需滿足|,-j2|=12(=1,2,…,;=1,2,…,)。定義第個DMA輸出端的數字權值為,其中=1,2,…,,則所有個DMA上數字權值組成的向量為

=[,,…,]∈×1

(5)

根據DMA陣列的結構,其等效混合發射權值向量為

(,)=(?)⊙∈×1

(6)

式中:=[1,1,…,1]∈×1。

在該模型下,遠場方向處的窄帶發射波束圖為

()=|()(,)|

(7)

需要設計混合權值向量(,),簡記為,使得()滿足指定的發射波束圖要求。將空間方位角[0°,180°]網格化,等間距劃分成個離散點。通過最小化期望波束圖和實際合成波束圖()之間的偏差,=1,2,…,,可將發射波束圖合成轉化為如下優化問題:

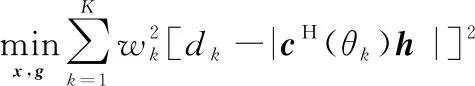
(8)

式中:∈表示不同方位角上的預加權因子,用于旁瓣控制。

為了簡化描述,將問題表示為如下形式:

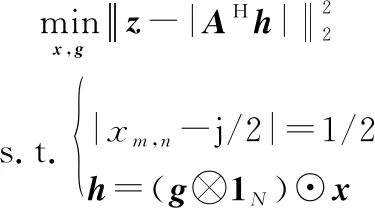
(9)

式中:

=[,,…,]∈×1

=[(),(),…,()]∈×

2 混合發射波束成形權值求解

問題是一個非凸優化問題,且待求變量和之間存在耦合。為了有效求解該問題,本文將基于交替優化的思想,提出一種基于ADMM的問題求解算法。算法的基本原理如下:首先通過引入輔助變量簡化問題描述;然后通過交替優化求解和{,},其中可以獲得閉式表達式,和的求解則利用ADMM實現。下面對該方法做詳細闡述。

為了去除問題中目標函數的取模運算||,引入一個輔助變量∈×1,表示期望波束形成的相位矢量。于是,問題變為

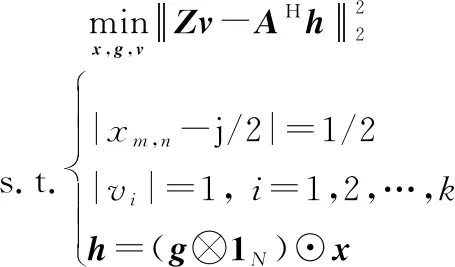
(10)

式中:=diag{}∈×。通過交替更新求解和{,},目標函數可收斂到一個有限值。文獻[17-18]已經證明了交替迭代求解的有效性。

當{,}固定,求解時,該子問題可表示為

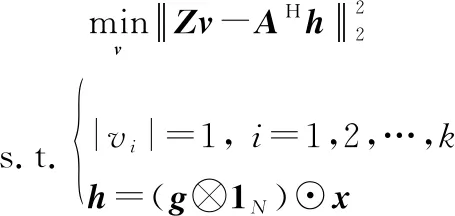
(11)

顯然,在式(11)中,當與中每個元素的相位均相同時,目標函數可達到最小值。由于是一個實矩陣,可看作為相位因子向量,因此式(11)的最優解為

∠()=∠()

(12)

當固定,求解{,}時,該子問題可表示為

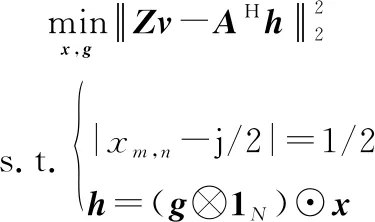
(13)

求解問題時存在模擬權值和數字權值耦合。通過解耦合,利用ADMM方法交替求解和,最終可得。

固定求解,混合發射權值向量的一種表示形式為

=⊙(?)=diag()(?)=

(14)

式中:

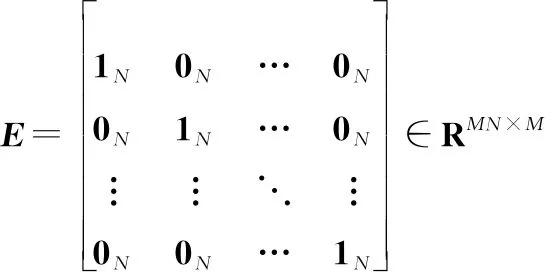
=diag(),=[0,0,…,0]∈×1。問題的子問題可以表示為

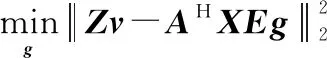
(15)

利用最小二乘求得

=()()

(16)

固定求解,混合發射權值向量另一種表示形式如下:

=(?)⊙=∈×1

(17)

式中:=diag(?)∈×。問題的子問題可以表示為

(18)

在式(18)中引入輔助變量,并令=,從而將約束與目標函數中的變量分離。于是,式(18)轉換為如下的優化問題:

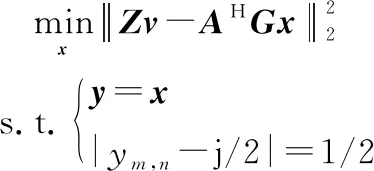
(19)

定義增廣拉格朗日函數為

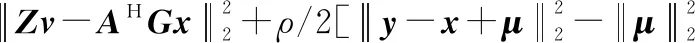
(20)

式中:∈×1是拉格朗日乘子或稱為對偶變量;>0是懲罰參數。

利用ADMM算法迭代求解、和的具體過程如下。

(1) 在已知((),())的情況下更新

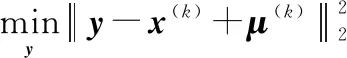
(21)

令()=()-(),則問題可以變成個子問題,其中第個子問題如下:

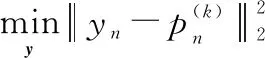
(22)

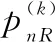
(23)

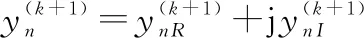
(24)

最終求得

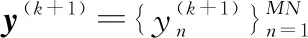
(25)

(2) 在已知((+1),())的情況下更新

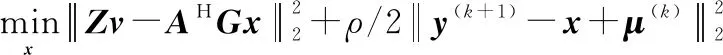
(26)

對式(26)最小二乘,求得

(+1)=(2+ρ)×[2+((+1)+())]

(27)

(3) 更新對偶變量

(+1)=()+(+1)-(+1)

(28)

定義原始殘差(+1)=(+1)-(+1)和對偶殘差(+1)=((+1)-()),設定算法迭代停止的準則為

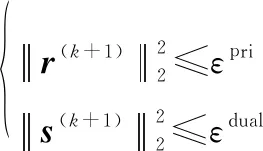
(29)

式中:和是預設的殘差容限。

本文算法求解問題的算法流程如下。

已知常量和,初始變量,,,,懲罰參數,收斂參數和,求解問題的解,,。

=1。

根據式(12)更新(+1)。

根據式(16)更新(+1)。

根據式(23)～式(25)更新(+1)。

根據式(27)更新(+1)。

根據式(28)更新(+1)。

根據式(6)更新(+1)。

設=+1。

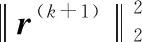
3 仿真與分析

為了驗證本文所提方法的有效性,下面進行不同情況下的發射波束成形仿真實驗。為了更好展示DMA陣列的性能,將與全數字陣列、唯相混合陣列和文獻[20]模型進行比較。

對于全數字陣列,其發射波束成形可表示為無約束優化問題如下:

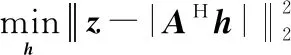
(30)

對于唯相混合陣列,其模擬部分由相控陣實現,發射波束成形可表示為約束優化問題如下:

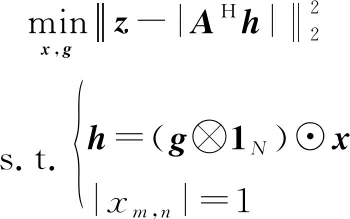
(31)

對于文獻[20]唯相陣列,其約束優化問題為

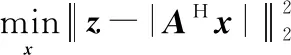
(32)

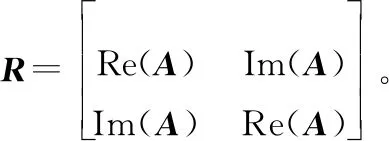
3.1 單波束成形

假定在0°方向合成單個主瓣,期望的波束圖為

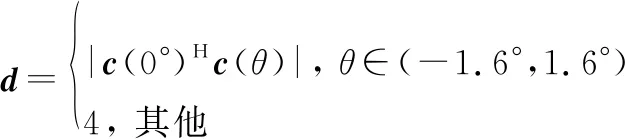
(33)

單波束成形結果如圖3所示。可以看出,與期望的波束圖相比,DMA混合、唯相混合和全數字3種方法都可以在主瓣0°方向很好地合成期望的主瓣,文獻[20]的主瓣峰值低于期望主瓣峰值0.97 dB。從主瓣的局部放大圖可見,全數字陣列的主瓣峰值為35.73 dB,DMA陣列合成的主瓣峰值為35.62 dB,而唯相混合陣列合成的主瓣峰值為35.56 dB。全數字陣列、DMA陣列、唯相混合陣列和文獻[20]陣列的峰值旁瓣比(peak-to-sidelobe ratio, PSR)分別為18.24 dB、17.21 dB、15.46 dB和15.21 dB。全數字陣列由于具有更大的自由度,相比于兩種混合陣列而言具有明顯的性能優勢。而本文提出的DMA陣列的主瓣峰值和PSR性能均優于唯相混合陣列。文獻[20]模型在常規波束形成下能達到比較好的性能。

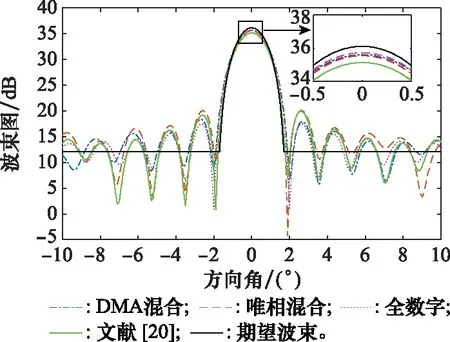
圖3 單波束成形Fig.3 Single beamforming

3.2 零陷成形

雷達系統通常需要在干擾方向上形成深零陷以實現干擾抑制。因此,接下來考慮零陷成形問題。假定在0°附近合成主波,在[-35°,-30°]方向上形成深零陷,則期望波束為

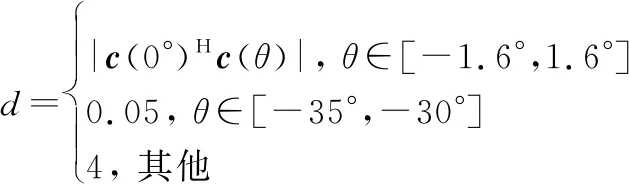
(34)

根據文獻[20],零陷區域的預加權設為=50,其余角度的預加權設為=1。

零陷成形結果如圖4所示,4種陣列結構均可以在0°方向上形成深零陷。實現零陷成形需要消耗發射權值的自由度,不可避免會對主瓣成形的性能產生影響。根據局部放大圖可見,全數字陣列的主瓣基本與期望主瓣重合,峰值僅下降0.4 dB;DMA陣列的主瓣下降0.39 dB;唯相混合陣列的主瓣下降1.93 dB,文獻[20]的主瓣下降2.43 dB。在非零陷方向上,DMA陣列、唯相混合陣列和文獻[20]陣列的PSR分別為15.56 dB、13.98 dB和10.86 dB。DMA性能優于后兩者。

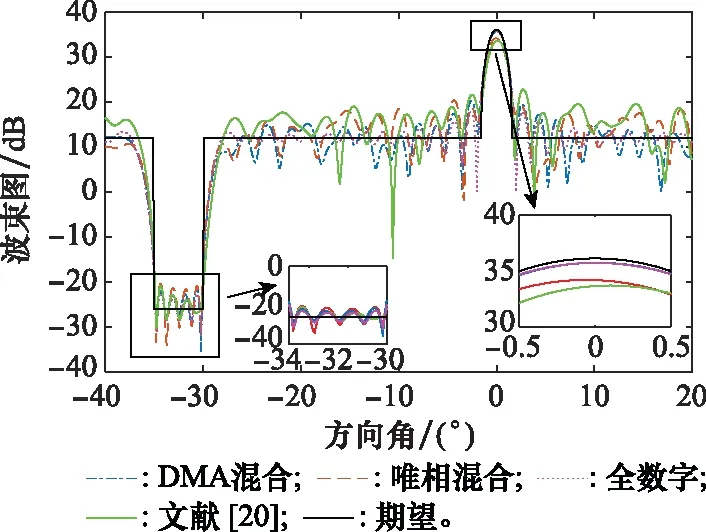
圖4 零陷成形Fig.4 Null forming

3.3 多波束成形

多波束合成廣泛應用于通信和雷達系統中,例如,基站需要發射多波束進行多用戶通信,雷達需要發射多波束來跟蹤位于不同方向上的多個目標。因此,下面考慮多波束成形的情況。

假定在-30°和30°方向上合成兩個主瓣,期望的波束圖定義為

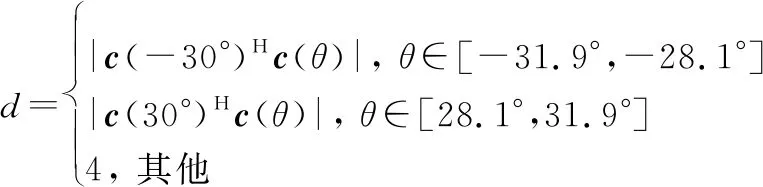
(35)

多波束成形結果如圖5所示,4種陣列均可以合成出期望的兩個主瓣。30°主瓣波束成形的局部放大如圖6所示,在30°方向附近,DMA陣列的主瓣峰值相比期望主瓣峰值下降了0.4 dB,PSR為17.58 dB;唯相混合陣列相對期望主瓣峰值下降了0.42 dB,PSR為14 dB;文獻[20]模型相對期望主瓣峰值下降了3.47 dB,PSR為13.7 dB。-30°主瓣波束成形的局部放大如圖7所示,在-30°附近,DMA陣列的主瓣峰值下降了0.44 dB,PSR為17.59 dB;唯相混合陣列的主瓣峰值下降了0.42 dB,PSR為13.87 dB;文獻[20]模型相對期望主瓣峰值下降了3.53 dB,PSR為13.71 dB。可以看出,DMA陣列主瓣峰值衰減小且可以獲得較大的PSR。

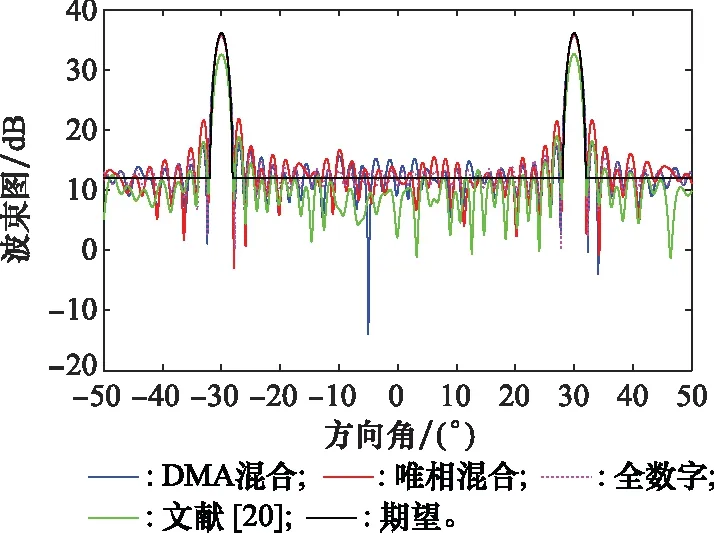
圖5 多波束成形Fig.5 Multi-beamforming

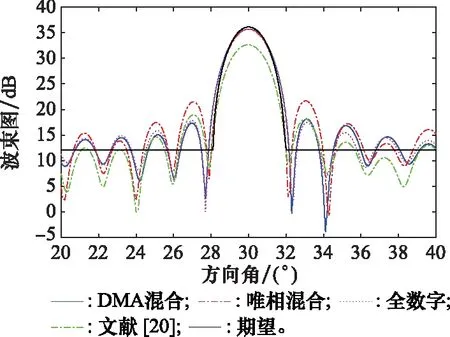
圖6 30°主瓣區域局部放大圖Fig.6 Partial enlarged view of 30° main lobe area

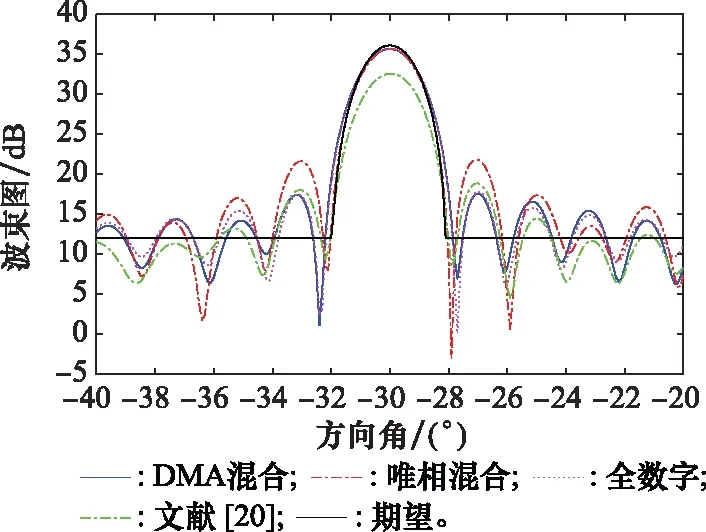
圖7 -30°主瓣區域局部放大圖Fig.7 Partial enlarged view of -30° main lobe area

4 結 論

本文利用DMA構建了一種新型模擬-數字混合陣列結構,并研究了基于DMA陣列的模擬-數字混合發射波束成形技術。不同于唯相混合陣列,DMA陣列的模擬波束成形由DMA直接實現,有利于簡化大規模MIMO系統和大規模天線DFRC系統的結構。本文基于DMA的特征,將DMA陣列混合發射波束成形建模為一個非凸約束優化問題,并利用交替優化對問題模型進行分解和簡化,提出了一種基于ADMM的模擬與數字權值聯合優化方法。該方法也可用于唯相混合陣列等其他混合陣列結構。試驗結果表明,DMA陣列在單波束成形、零陷成形和多波束成形方面的性能均優于唯相混合陣列和恒模約束的唯相陣列,是一種有效的混合陣列結構。在未來研究中,將進一步開展DMA陣列接收波束成形和發射-接收聯合波束成形方面的工作。