脈沖噪聲下基于NAT函數的LFM信號參數估計
金 艷, 趙大地, 姬紅兵
(西安電子科技大學電子工程學院, 陜西 西安 710071)
0 引 言
線性調頻(linear frequency modulation,LFM)信號具有分辨率高和截獲概率低等特點,是一類具有代表性的非平穩信號,常應用于水聲、雷達、生物醫學、地質勘探等領域。中心頻率和調頻斜率包含有LFM信號的相位參數信息,所以LFM信號的參數估計方法研究具有重要價值。基于最大似然(maximum likelihood,ML)原理的LFM信號分析方法計算精度高,其誤差估計曲線接近克拉美羅下界(Cramer-Rao lower bound,CRLB),但該方法需要優化損失函數,計算量大且實時性差。分數階傅里葉變換(fractional Fourier transform, FrFT)是一種應用廣泛的非平穩信號分析方法,LFM信號的能量聚集性隨著FrFT階數的不同而改變,通過搜索FrFT域的峰值坐標,再由峰值坐標與信號相位參數的轉換公式,完成信號參數估計,該方法步驟較為復雜。呂氏分布(Lv’s distribution, LVD)方法是一種將LFM信號直接分解在中心頻率-調頻斜率(centroid frequency chirprate,CF-CR)域進行研究的時頻分析方法。經LVD變換后,LFM信號在LVD域呈現為峰值。與FrFT方法不同,LVD免去從峰值坐標到信號相位參數轉換的步驟,由CF-CR平面上的坐標即可直接獲得LFM信號的中心頻率和調頻斜率。
然而,上述LFM信號參數估計方法在脈沖噪聲環境下性能急劇下降甚至失效。對于具備明顯脈沖特性,且概率密度函數拖尾厚重的噪聲,α穩定分布噪聲模型能夠對其準確描述。但α穩定分布的二階和高階矩不具備有界性,所以傳統的信號處理方法在α穩定分布噪聲下不再適用。對此,近年來有研究者提出了基于相關熵核函數內在穩健性的信號處理方法;也有學者提出了首先采用非線性方法對接收信號進行脈沖噪聲抑制,使含有α穩定分布噪聲的信號經非線性處理后,信號的二階統計量存在,再采用常規信號處理方法完成有用的信號分析和提取,如分數低階(fractional lower order,FLO)方法、基于M估計的Myriad濾波和Meridian濾波方法、基于非線性幅值變換(nonlinear amplitude transformation,NAT)函數的方法等。
以上方法雖然可較為有效地抑制α穩定分布噪聲,但也存在明顯缺陷,如傳統相關熵的核函數為高斯核,僅適用于信噪比較高的環境下,且由于核函數自身缺陷,相關熵方法無法抑制幅值相近的脈沖噪聲;FLO方法雖能較好地抑制噪聲,但需要獲得噪聲先驗信息,且其階數的取值缺乏理論依據,實時性差;Myriad及Meridian濾波方法計算復雜度高,且在脈沖性強的噪聲環境下性能下降劇烈;基于非線性幅值變換函數的方法是將含噪信號進行預處理,在不改變參數信息的基礎上抑制噪聲,已有研究將神經網絡中常用的激活函數,如Sigmoid函數和tanh函數用于非高斯信號處理領域,這兩種函數相較于FLO方法無需在參數估計前獲取噪聲信息,但Sigmoid函數和tanh函數抑制脈沖噪聲的能力弱于分數低階方法,因此這兩種NAT函數抑制脈沖噪聲的能力有限。
針對現有的抑制脈沖噪聲方法存在的計算復雜度高、需獲取噪聲先驗信息和抑噪能力有限等問題,論文設計了兩種新的NAT函數,即具有衰減特性的A-NAT函數和具有限幅特性的IB-NAT函數,并從計算復雜度和抑制脈沖噪聲能力兩方面將兩種函數進行對比,確定其適用范圍。將經過函數變換后的信號進行LVD分析,通過CF-CR域上對應的峰值坐標即可直接實現LFM信號的參數估計。本文所提方法計算復雜度低,實時性高,且無需獲取噪聲先驗信息。
1 α穩定分布脈沖噪聲模型
由于α穩定分布不具備閉式的概率密度解析式,因此一般采用特征函數表示:
()=exp{j-||[1+jsgn()(,)]}
(1)
其中,
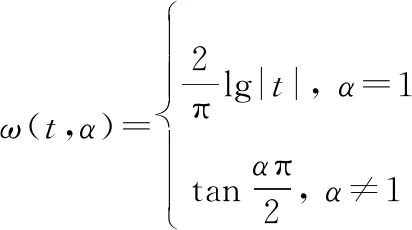
(2)
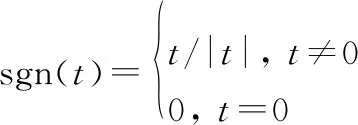
(3)
式中:sgn()為符號函數;表示位置參數,且-∞<<+∞,其值決定了分布的中心位置;特征指數的取值為0<≤2,值越小則噪聲的脈沖特性越強,特別地,當=1時,該分布變為柯西分布,=2時變為高斯分布;尺度參數取值為>0,用于衡量樣本偏離均值的程度,類似于高斯分布的方差;為對稱參數,且-1≤≤1,表征分布的對稱程度,=0時即為對稱穩定分布(symmetric α stable,SαS)。由于穩定分布噪聲的方差不存在,常規信噪比無意義,所以采用廣義信噪比(generalized signal to noise ratio,GSNR):
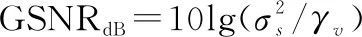
(4)
2 非線性幅值變換函數
由于含有隨機大幅值脈沖,穩定分布的二階統計量不具備有界性,所以基于二階矩的常規參數估計方法在穩定分布噪聲環境下失效。FLO方法將穩定分布噪聲處理轉化為對其脈沖幅度的抑制,可實現脈沖噪聲中有用信號的分析與提取。受此啟發,本文構造兩種新的可抑制大幅值脈沖的NAT函數,使含有穩定分布噪聲的信號非線性變換后,信號的二階統計量存在,進而使得后續信號分析中常規參數估計方法有效可行。
當含噪信號包含大幅值脈沖時,所構造的非線性函數需能夠有效抑制噪聲的大幅值,因而可考慮具有如下衰減特性的attenuation-NAT (A-NAT)函數或具有有界單調遞增特性的increasing bounded-NAT(IB-NAT)函數:
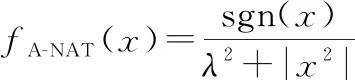
(5)
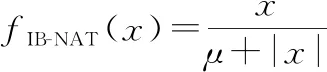
(6)
式中:sgn()為式(3)所示的符號函數,若為復數,||為的模值;()的值域為(-1,1),()值域為(-1,1)。由式(5)和式(6)可知,()的分母中含有二次項,()只包含一次項,因此A-NAT函數的計算復雜度要高于IB-NAT函數。
圖1所示為本文構造的A-NAT函數()與IB-NAT函數()曲線。圖1(a)為A-NAT函數()曲線,由圖可知,所構造的A-NAT函數具有非線性特性且是奇對稱的,該函數在=0附近(即臨零區域)迅速達到極值后,在定義域的其余范圍均處于衰減狀態,且隨著||增大,函數值趨于0。因此,A-NAT變換可將強脈沖值壓縮映射至()值域范圍(-1/,1)內,且脈沖值越大,經A-NAT變換后的函數值越小。由圖1(b)可以看出,所構造的IB-NAT函數具有單調遞增和對稱有界特性。IB-NAT函數在臨零區域內近似線性,隨著||的增大,函數值趨于值域邊界。
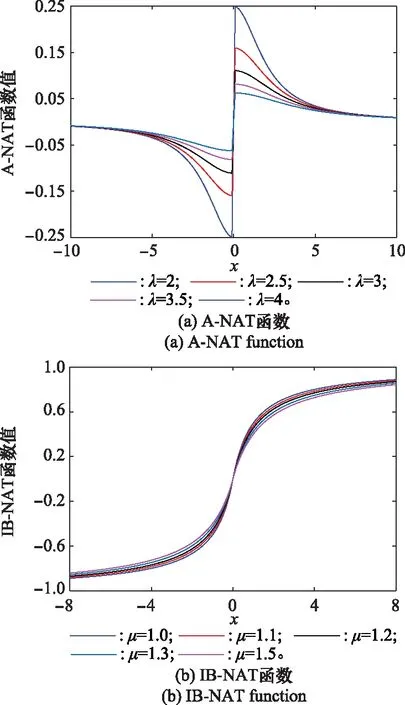
圖1 兩種新的NAT函數曲線Fig.1 Two new NAT function curves
圖2和圖3是在GSNR為-3 dB,特征指數取不同值時,對LFM信號進行200次蒙特卡羅實驗,得到信號中心頻率、調頻斜率與歸一化均方根誤差(normalized root mean square error,NRMSE)的關系曲線。由實驗結果可知,A-NAT函數中的參數最優取值為2≤≤3;IB-NAT函數中的參數最優取值為1≤≤1.5。
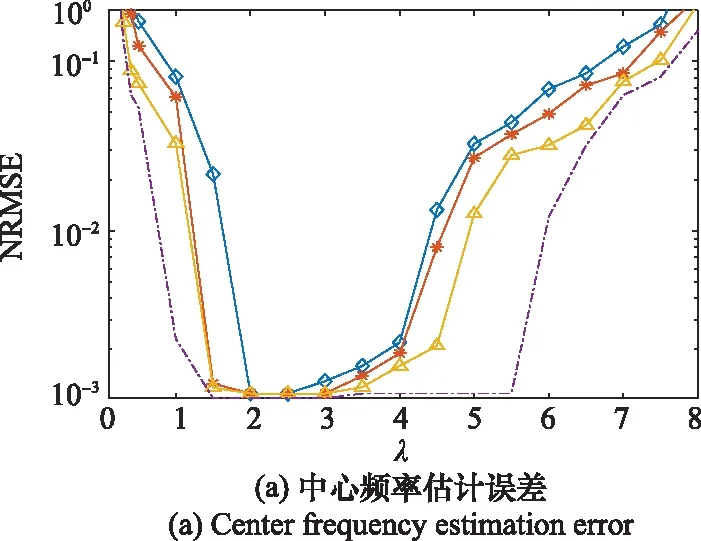
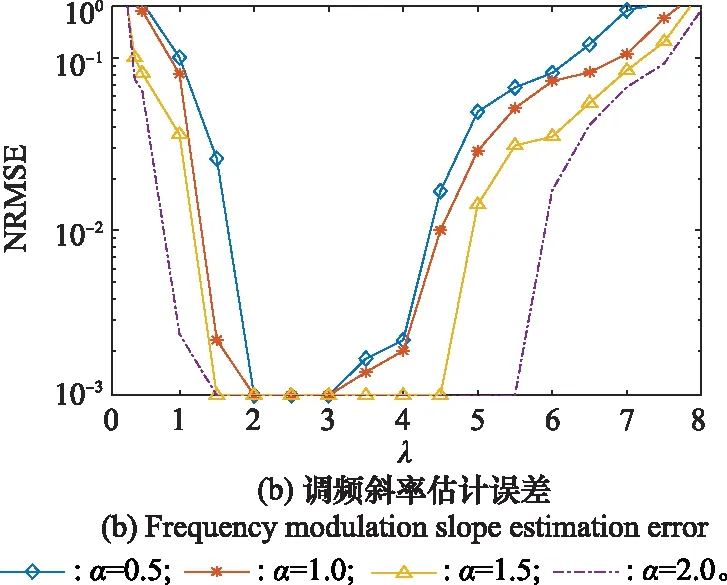
圖2 A-NAT函數不同參數下信號估計誤差Fig.2 Estimation error of A-NAT function for signals under different parameters
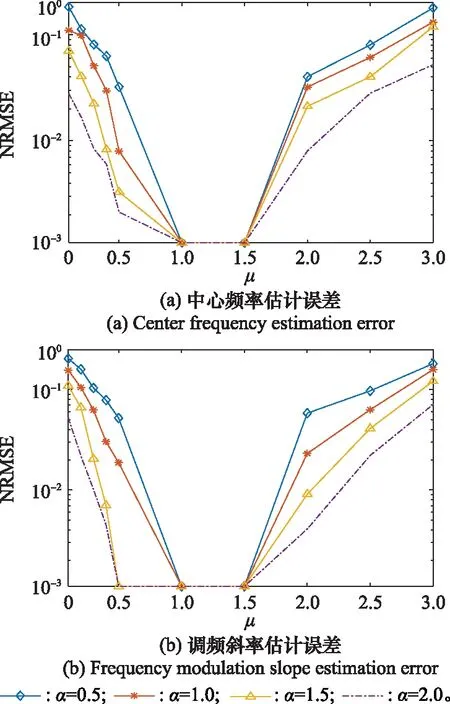
圖3 IB-NAT函數在不同參數下對信號估計誤差Fig.3 Estimation error of IB-NAT function for signals under different parameters
分別取=2和=1,得到圖4和圖5所示NAT變換后的穩定分布噪聲方差。可知,穩定分布經A-NAT和IB-NAT非線性幅值變換后的方差均有界,且在=0.3的脈沖性極強的條件下仍收斂,即通過A-NAT或IB-NAT變換后,穩定分布的二階矩有界,因此所構造的A-NAT函數和IB-NAT函數均能對脈沖噪聲起到抑制作用。
對比圖4和圖5可知,穩定分布經A-NAT變換后的方差隨值減小而減小,而經IB-NAT變換后的樣本方差則隨值減小而增大。這是因為當值減小時,穩定分布出現偏離分布中心的大幅值異常脈沖值的概率增大,不同的異常值經A-NAT函數衰減變換后分布于值域內的不同位置處;而IB-NAT函數是將所有異常值均變換到值域邊界,在較小的情況下,大量異常值密集地分布于值域邊界附近,從而造成方差增大。可知,IB-NAT函數是通過限幅作用將脈沖噪聲限制在值域邊界,而A-NAT函數具有衰減特性,噪聲的脈沖性越強,()對噪聲所起到的抑制作用也越強。因此,在∈[0.1,0.8)的脈沖性極強的條件下,A-NAT函數抑制噪聲的性能優于IB-NAT函數。
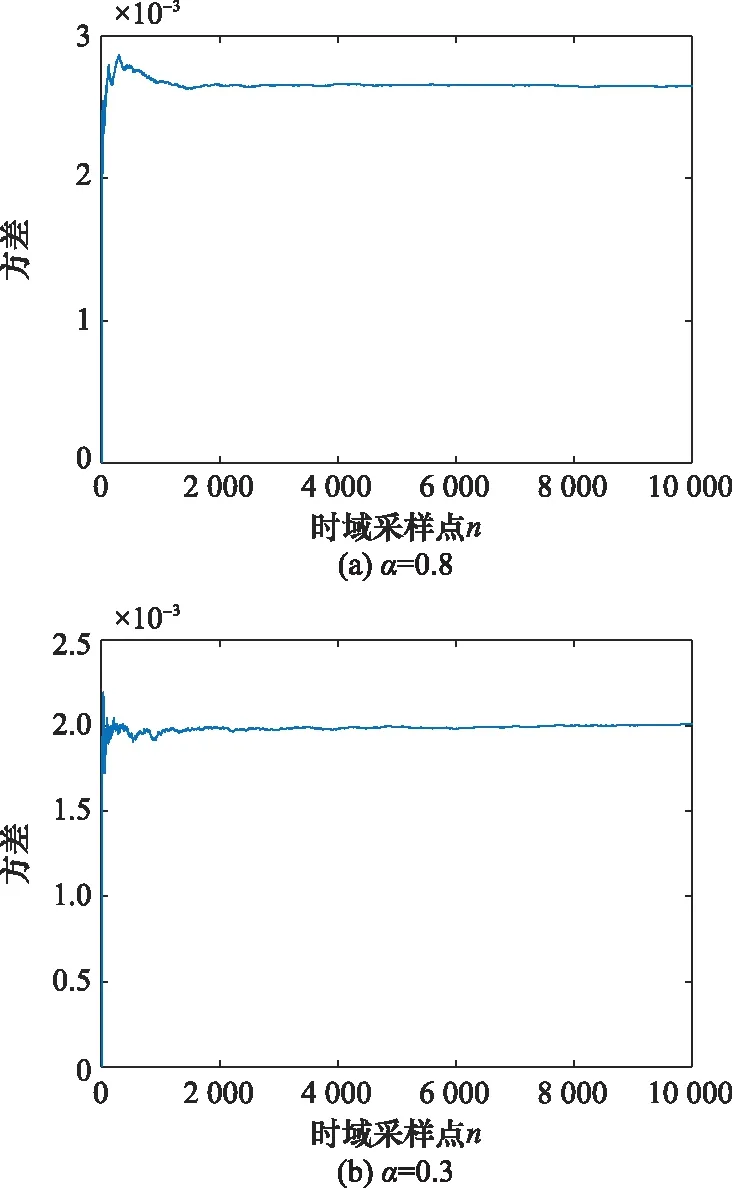
圖4 A-NAT變換后的α穩定分布方差Fig.4 Variance of α-stable distribution after A-NAT transformation
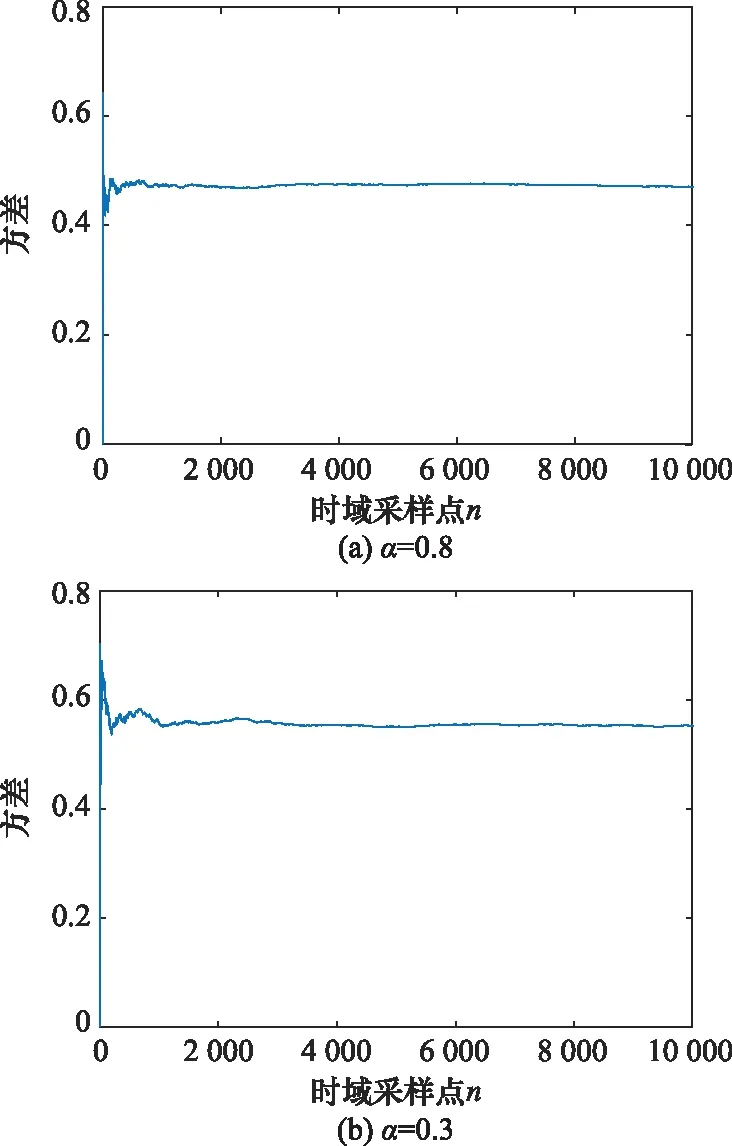
圖5 IB-NAT變換后的α穩定分布方差Fig.5 Variance of α-stable distribution after IB-NAT transformation
FLO算子能夠較為有效地抑制脈沖噪聲,但FLO算子需要獲取噪聲先驗信息。與FLO算子()=[][26]相比,A-NAT函數在臨零區域之外的定義域內均處于衰減狀態,IB-NAT函數的遞增趨勢更緩慢且有界。因此,本文所構造的兩種非線性幅值變換函數可更有效抑制脈沖噪聲,且基于這兩種函數的參數估計方法無需噪聲先驗信息。由此提出命題1并給予證明。
為服從穩定分布的大幅值脈沖樣本,設經過A-NAT變換后的函數值為=(),經IB-NAT變換后的函數值為=(),則在脈沖噪聲環境下滿足(||)<(||)<(|([])|),其中0<<2,<>=·||||。
設的概率密度函數為(),則有
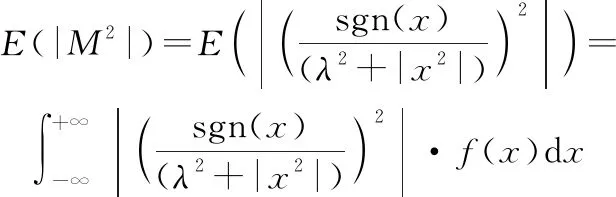
(7)
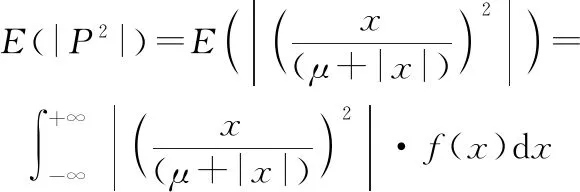
(8)
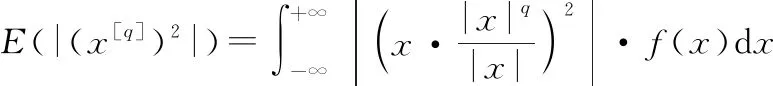
(9)
由于概率密度函數()≥0,所以只需證明在-∞<<+∞時,
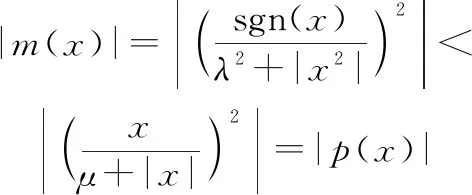
(10)
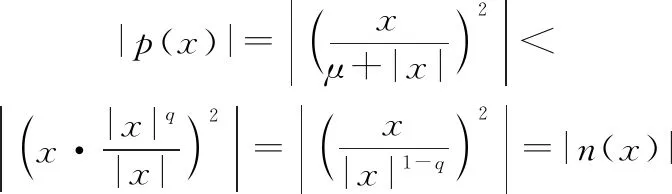
(11)
因為()=(-),()=(-),則只需證明0≤<+∞時,以上不等式成立,當0≤<+∞時,式(10)和式(11)可分別化為
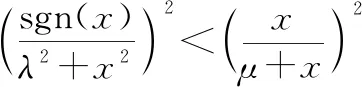
(12)
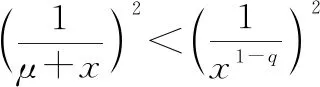
(13)
即等價于證明

(14)
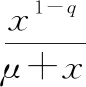
(15)
因為為服從穩定分布的大幅值脈沖樣本,∈[2,4],∈[1,15],∈(0,2),則式(14)和式(15)成立,即式(10)和式(11)成立,從而命題1得證。因此,具有脈沖特性的樣本經過A-NAT或IB-NAT變換后均存在有限二階矩,且A-NAT函數和IB-NAT函數脈沖噪聲抑制性能均優于FLO函數,其中A-NAT函數的抑制效果最優。
LFM信號經A-NAT或IB-NAT函數變換后僅幅值發生變換,相位信息不變。
設LFM信號為()=exp(j2π+jπ),為信號幅度,為信號的初始頻率,是調頻斜率,則有
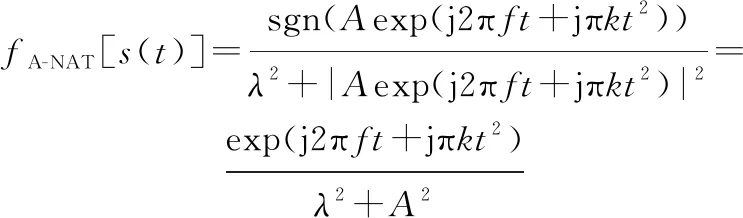
(16)
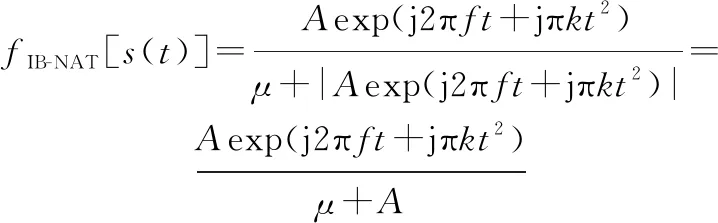
(17)
證畢
3 基于NAT函數的參數估計
3.1 LVD變換
LVD方法是一種比傳統時頻分析更為高效的LFM信號處理方法。常規的LFM信號分析方法是在時頻域對其進行參數估計,而LVD方法是將信號分解在CF-CR域,LFM信號經LVD變換后表現為峰值,通過該峰值所對應的CF-CR平面坐標,即可得到LFM信號的調頻斜率與中心頻率估計值。
LFM信號()的表達式可寫為
()=ej2π+jπ
(18)
式中:表示信號幅值;和分別表示LFM信號的中心頻率和調頻斜率。()的對稱參數瞬時自相關函數(parametric symmetric instantaneous autocorrelation function,PSIAF)定義為
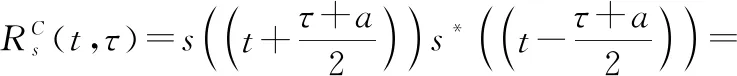
(19)
式中:為延遲常數,一般取其最優值1;*為共軛符號。通過對時間變量做如下尺度變換可以解除其與延時的耦合關系:
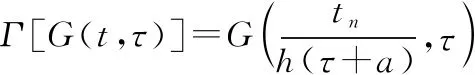
(20)
式中:為尺度因子,時間變量經過尺度變換,為=(+),此時PSIAF為
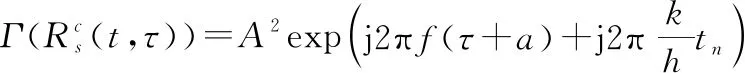
(21)
再對,作二維傅里葉變換,即得LVD的表達式:
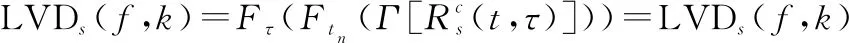
(22)
式中:{·}表示傅里葉變換。LFM信號的LVD為
望虞河常熟水利樞紐于2010年11月起開始實施更新改造工作,改造工程于2011年3月10日前完成。改造期間常熟水利樞紐泵站無法正常投入運用,僅能通過節制閘自引。望虞河望亭水利樞紐更新改造工程于2010年11月28日正式開工。根據施工期工程運行維護要求,望亭水利樞紐需開展水下檢查暫停運用。同時,施工期間望亭水利樞紐閘門也無法全部投入運用。
LVD(,)=exp(j2π)·(-)(-)
(23)
可以看出,僅當=,=時,LVD取非零值。
利用峰值檢測方法搜索LVD時頻譜峰值坐標(,),為LFM信號中心頻率的估計值,是調頻斜率的估計值。
3.2 基于NAT函數的參數估計
設信號()是脈沖噪聲環境下的LFM信號,即
()=()+()
(24)
式中:()是穩定分布脈沖噪聲。()和()分別是信號()經A-NAT變換、IB-NAT變換后的信號,即
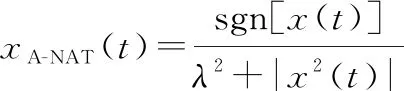
(25)
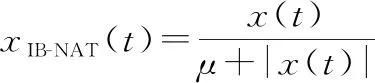
(26)
式(25)和式(26)作LVD變換,在LVD域搜尋峰值點,根據該峰值對應的CF-CR平面坐標值即可完成LFM信號的參數估計。
4 仿真實驗與結果分析
本文仿真采用聲納工程中的LFM信號參數:中心頻率=7.5 kHz,調頻斜率=1 kHz/s,采樣頻率=25.6 kHz,采樣點數=2.56×10。噪聲環境為SαS分布噪聲。
4.1 不同方法仿真結果及分析
如圖6(b)~圖6(f)所示,在α=0.8,GSNR=-2 dB的噪聲環境下,分別采用LVD方法、基于Myriad濾波的MY-LVD、基于FLO方法的FLO-LVD與本文提出的A-NAT-LVD、IB-NAT-LVD方法對含有脈沖噪聲的LFM信號進行處理并對比。
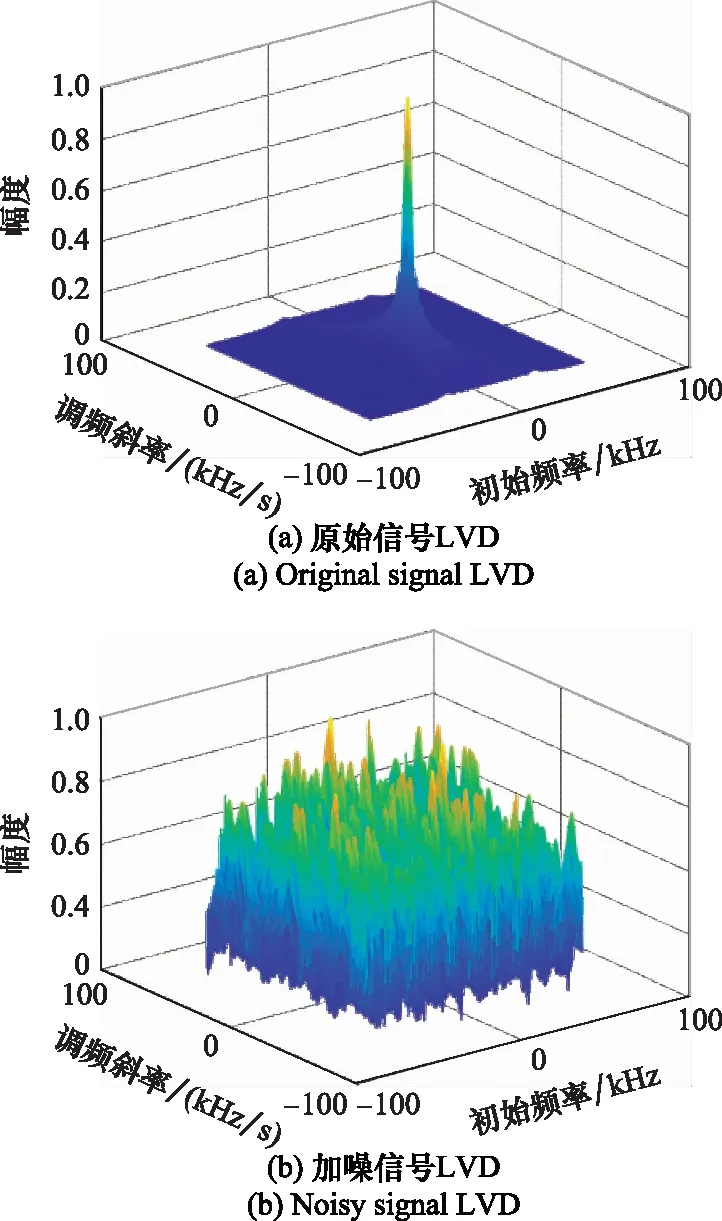
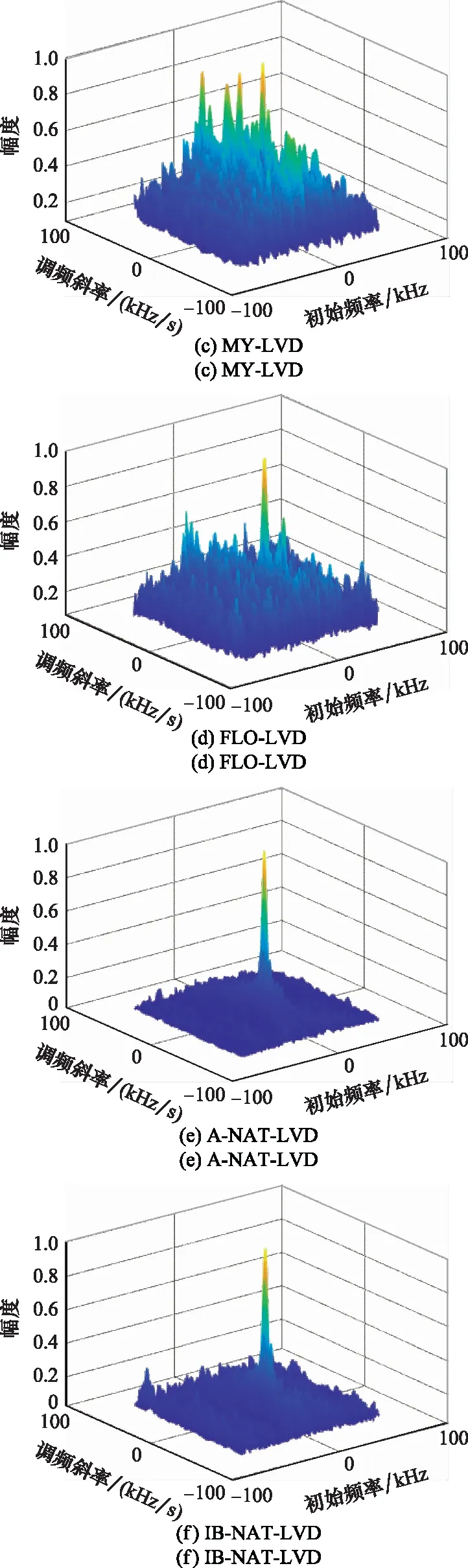
圖6 不同方法下的LVDFig.6 LVD under different methods
圖6(a)是在無噪聲的理想環境下原始LFM信號的LVD三維圖,圖中峰值明顯,通過峰值坐標即可估計出信號的中心頻率和調頻斜率值;圖6(b)是在脈沖噪聲下,信號的LVD三維圖,含有參數信息的峰值被噪聲覆蓋,無法進行參數估計;圖6(c)是基于Myriad濾波的MY-LVD所對應的LVD三維圖,圖中存在多個峰值,無法根據最大峰值點對應的CF-CR平面坐標提取LFM信號參數信息;采用基于FLO(階數為0.2)算子的FLO-LVD方法得到了圖6(d),可見,脈沖噪聲已被抑制,雖存在部分凸起峰值,但最大峰值明顯,可以提取參數信息;分別采用A-NAT-LVD方法和IB-NAT-LVD方法得到了圖6(e)和圖6(f),可以看出,采用本文所提兩種方法,脈沖噪聲得到有效抑制,幾乎無殘余噪聲,且均存在明顯峰值。綜上,A-NAT-LVD和IB-NAT-LVD方法可有效抑制脈沖噪聲,且性能優于FLO-LVD方法,與本文命題1所述理論一致。
4.2 不同方法性能比較及分析
本節通過NRMSE來描述不同方法抑制脈沖噪聲的性能差異。在不同的GSNR環境下,經200次蒙特卡羅實驗,實驗結果如圖7和圖8所示。
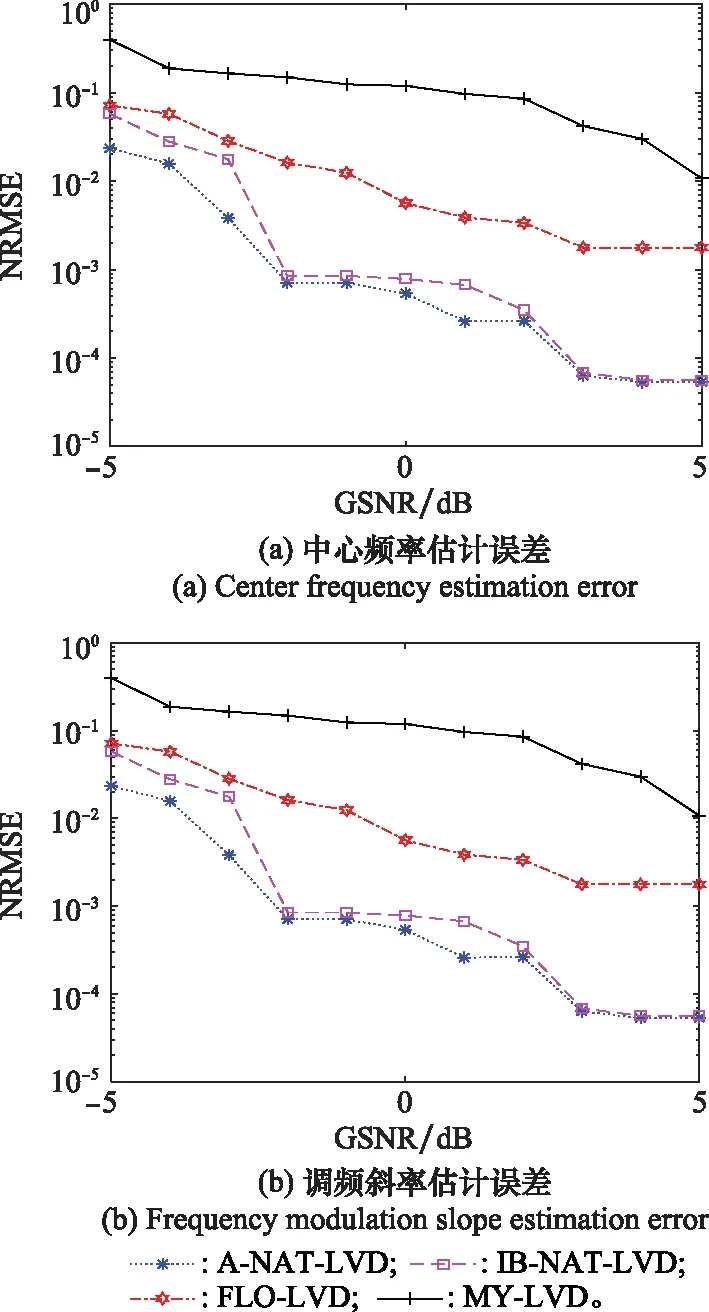
圖7 α=0.8時LFM信號參數估計誤差Fig.7 Error of LFM signal parameter estimation when α=0.8
根據圖7,MY-LVD方法在=0.8和較高GSNR的噪聲條件下,對LFM信號的參數估計仍存在偏差;FLO-LVD方法在=0.8的脈沖噪聲環境下,當GSNR≥-1 dB時可以實現有效參數估計,但當GSNR<-1 dB時估計性能下降明顯;A-NAT-LVD和IB-NAT-LVD方法在GSNR≥-2 dB時可較為精確地對LFM信號的中心頻率和調頻斜率進行參數估計。由圖8可知,在=15的穩定分布噪聲環境下,MY-LVD方法對LFM信號的參數估計誤差比在=0.8的條件下有所減小,但仍存在偏差;FLO-LVD方法在GSNR≥-2 dB條件下可較為精確地對LFM信號的中心頻率和調頻斜率進行參數估計;IB-NAT-LVD方法在GSNR≥-3 dB時,A-NAT-LVD方法在GSNR≥-4 dB時可較為精確地估計出LFM信號參數。
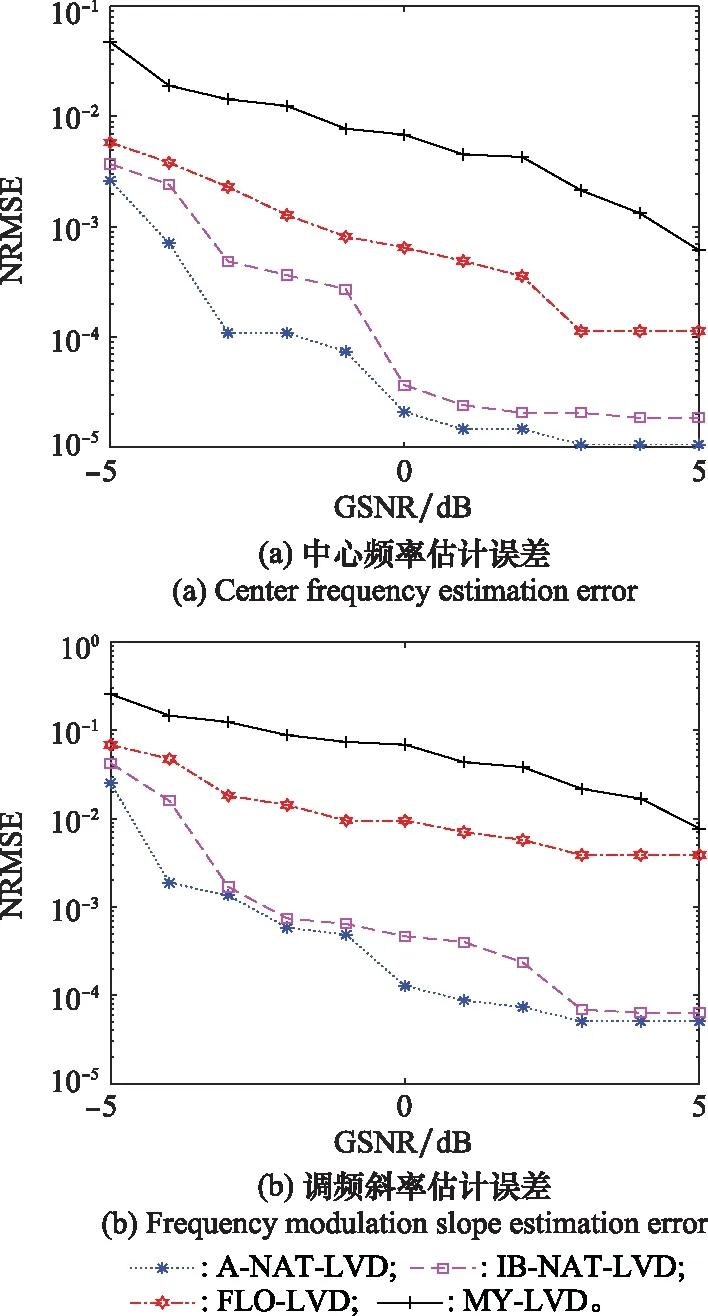
圖8 α=1.5時LFM信號參數估計誤差Fig.8 Error of LFM signal parameter estimation when α=1.5
比較圖7和圖8可知,采用A-NAT-LVD和IB-NAT-LVD方法可以在脈沖性較強,GSNR較小的環境下實現對LFM信號參數的準確估計,隨著脈沖強度的增大,FLO-LVD和MY-LVD方法的性能下降,而A-NAT-LVD和IB-NAT-LVD方法仍具有較強的穩健性。
為進一步分析所提方法適用的穩定分布噪聲范圍,以及驗證命題1中提出的()抑制脈沖噪聲的能力強于(),在GSNR=-2 dB的條件下,改變特征指數的值并進行200次蒙特卡羅實驗,結果如圖9所示。可見,A-NAT-LVD方法和IB-NAT-LVD方法在≥0.8脈沖噪聲環境下性能接近,且抑制噪聲能力均優于FLO-LVD方法和MY-LVD 方法;在<0.8沖擊性極強的噪聲環境下,由于A-NAT函數對大幅值脈沖的衰減作用,A-NAT-LVD仍具有穩健的參數估計性能。IB-NAT-LVD 方法在<0.8的環境下抑制脈沖噪聲的能力不及A-NAT-LVD方法,但仍優于FLO-LVD和MY-LVD方法。
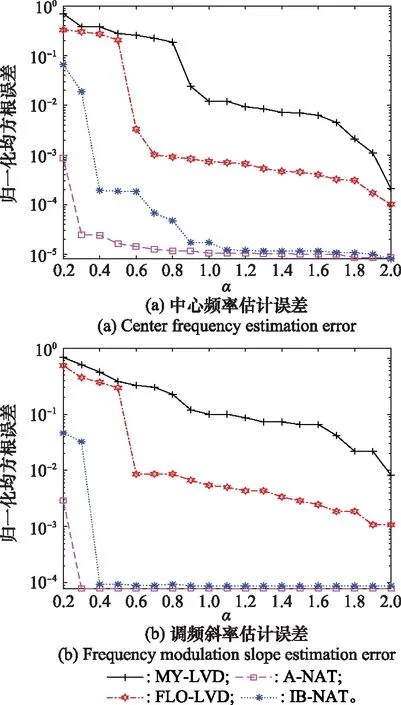
圖9 不同α值下參數估計誤差比較Fig.9 Comparison of parameter estimation error under different α values
因此,在<0.8脈沖特性極強的噪聲環境下,選擇抑噪性能最優的A-NAT-LVD方法;在≥0.8的噪聲環境下,可選擇計算復雜度更低的IB-NAT-LVD方法替代現有的脈沖噪聲下LFM信號參數估計方法。
5 結 論
為解決脈沖噪聲環境下傳統LFM信號參數估計方法性能下降劇烈甚至失效的問題,本文構造了A-NAT函數和IB-NAT函數,提出了基于所構造NAT函數的參數估計新方法。通過對命題1和命題2的證明可知,含噪信號經A-NAT或IB-NAT變換后的二階矩存在有界值,且僅幅值變化,相位信息不變,IB-NAT函數相較于A-NAT函數具有更低的計算復雜度,而在抑制脈沖噪聲能力方面,()>()>()。首先對脈沖噪聲背景下的LFM信號進行A-NAT或IB-NAT變換,再對變換后的信號進行LVD分析,即可完成LFM信號的參數估計。與基于FLO函數和Myriad濾波的參數估計方法對比,本文所提方法無需噪聲先驗信息,能夠抑制不同強度的脈沖噪聲,且具有良好的魯棒性。

