扁平鋼箱梁風屏障防風效果的數值模擬研究

胡 博， 向活躍,2， 李永樂,2

(1.西南交通大學 土木工程學院，成都 610031；2.西南交通大學 風工程四川省重點實驗室，成都 610031)

大風災害天氣對橋上車輛行駛安全極為不利，導致車輛側翻和封橋禁止通行的情況時有發生，嚴重威脅人民生命財產安全，阻礙了區域物流、人流的暢通，造成了不良的社會影響和巨大的經濟損失[1]。在高效、快節奏的現代社會中，全天候、準點、安全行車的要求尤為突出。研究側風作用下橋上車輛行駛安全性和舒適性保障措施的作用機理、實際效果和影響參數是十分必要的。

在強風下運行的車輛受到側向力、升力和傾覆力矩的作用，影響高速行車安全。為了增強側向風作用下行車的安全性，通常有3種方法[2]：一是優化車輛橫斷面形狀，該措施對保證行車安全性可以起到一定的作用，但是很難從根本上解決側向風對行車安全性的威脅，且對已有車輛是不適用的；二是安裝大風預警系統，實時監測預警大風，但目前在強風的預警精度方面還有待進一步提高,且存在監控盲區；三是安裝風屏障，減小作用在車輛上的風荷載，為車輛創造一個相對低風速的局部環境。上述3種方法中，安裝風屏障是增強側向風作用下行車安全性成本較低、效果很好的措施[3]。

國內外學者通過現場實測、風洞試驗和計算流體力學(computational fluid dynamics，CFD)等方法對風屏障的防風效果、風屏障后方的流場分布和風屏障對車輛橋梁氣動力特性的影響等開展了廣泛深入的研究。李永樂等[4]通過風洞試驗和風-車-橋(線)耦合振動的分析方法研究了風屏障高度、車輛線路位置及線路構造形式對風屏障防風效果的影響。向活躍等[5]對鐵路風屏障對軌道上方風壓分布影響開展了風洞試驗研究，研究表明：迎風側風屏障有效地減小了軌道上方的風壓值，背風側風屏障會增加軌道上方的負壓；蘇洋等[6]以車輛側傾穩定性力矩系數及橋梁阻力系數為優化目標，風屏障高度為設計變量，采用多目標遺傳算法求解Pareto最優解集，采用數據包絡分析方法評價Pareto解集中各個解的相對效率，得到最優風屏障高度。郭薇薇等[1]通過風洞試驗測試了有、無風屏障時車輛、橋梁的三分力系數，對強側風作用下車輛通過橋梁時的動力響應進行了數值模擬，綜合分析得到了保證列車在橋上運行安全的風速-車速閾值曲線；何旭輝等[7]基于同步測壓技術，研究了風屏障對典型車橋組合狀態下列車的風壓分布和各面氣動力分布特征的影響；張田等[8]研究了風屏障導致的風載突變對列車運行安全的影響；向活躍等[9]基于支持向量機模型方法對風屏障的高度和透風率進行了優化研究。何瑋等[10]指出在側風作用下，車體迎、背風面的壓力分布不僅受風屏障高度的影響，而且受列車在橋面的位置的影響。Xiang等[11]應用自適應支持向量機代理模型對鐵路風障防護效果進行了優化。周奇等[12]對不同透風率不同風攻角下曲線風障的減風效果進行了數值模擬。柳潤東等[13]數值模擬了高速列車通過風障區域的整個過程，研究了作用在風障表面的列車風致脈動壓力。史康等[14]通過風洞試驗探究了橫風作用下新型百葉窗型風屏障不同葉片旋轉角度、不同風屏障布置形式對車橋系統氣動特性的影響，運用CFD數值模擬闡述了該風屏障的防風機理。Ogueta-Gutiérrez等[15]對不同風屏障類型下列車的氣動力特性進行了風洞試驗研究。Papesch[16]以傾覆力矩為評價指標，通過風洞試驗研究了不同防風結構的防風效果。Chu等[17]采用CFD數值模擬和風洞試驗相結合的方法，研究了風屏障后方車輛上的風荷載，評估了風屏障的防風效果。

以上研究多針對鐵路橋梁，對大跨度公路橋梁風屏障研究相對較少，且較少涉及多個參數的聯合影響，較少利用基于樣本建立的代理模型來對影響風屏障防風效果的因素進行系統地研究。

本文針對典型流線型箱梁斷面和典型分離障條直線型風屏障，將風速折減系數作為評價風屏障防風效果的指標[18]，基于CFD計算了7類高度和13類透風率組合共42種工況下的不同車道位置處的風速折減系數。基于神經網絡方法，建立了預測各車道風速折減系數的代理模型，得到了各車道的“風速折減系數-風屏障透風率-風屏障高度”圖表,考查了風屏障高度、透風率和各車道風速折減系數之間的關系,給出了風速折減系數等值線，可為風屏障的設計提供一定的參考。

1 CFD數值分析模型

1.1 模型參數

在本研究中CFD模擬選用的扁平鋼箱梁寬32 m，高4 m，風屏障類型為分離障條直線型風屏障，在橋面布置有6個車道，如圖1所示。

圖1 模型橫斷面(m)

大跨度橋梁結構的扁平鋼箱主梁通常是等截面的平直細長構件，本文根據條帶假定將主梁簡化為二維模型。對于風屏障而言，其孔隙的布置有多種形式：圓孔式，縱條式(類似于防撞欄桿)。對于縱條式，可當做線狀結構，直接采用二維模型模擬；對于圓孔式風屏障，若按原型進行模擬，則網格量非常巨大，已有的風洞試驗表明：按高度相同、透風率等效的原則簡化成二維模型進行模擬可以實現圓孔式風屏障和縱條式風屏障的等效[2]。因此本文將帶有分離障條直線型風屏障的扁平鋼箱梁簡化成如圖1所示的二維模型進行繞流模擬。

流場計算域如圖2所示，區域長度取為20倍的箱梁模型寬度，寬度取為20倍的箱梁模型高度，左側入口邊界到箱梁模型中心的距離取為6倍箱梁模型寬度[12]。左側邊界設置為速度入口邊界，為30 m/s的均勻來流，上、下及右側邊界均采用壓力出口邊界，箱梁和風屏障采用固定壁面邊界條件模擬。

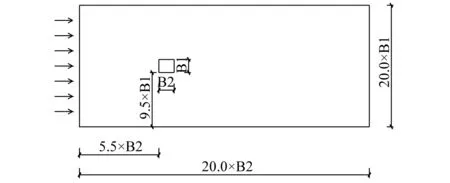
圖2 模型計算區域

為兼顧計算效率和精度，將計算區域劃分成九宮格，中宮采用四邊形非結構化網格，另外各宮為四邊形結構化網格，如圖3所示。網格從固定剛體壁面向外，由密逐漸變疏，由小逐漸變大，網格數量約32.3萬。

圖3 透風率30%、高度3 m工況下的計算網格

為了準確模擬橋面的風場環境，計算采用可以高精度求解邊界層、準確模擬流動分離的SSTk-ω湍流模型[19]。壓力-速度耦合項采用SIMPLEC算法求解，壓力項采用二階格式離散，動量及湍動能采用二階迎風格式，耗散率項采用Power law格式進行計算。

1.2 計算工況

實際工程中風屏障的高度多為3.5 m左右，比如平潭跨海大橋；但在部分特殊地區的橋面上會設置半封閉聲屏障，其高度可能超過5 m，部分甚至達到8 m[20]；部分現場實測表明，風屏障最有效的水平防護范圍在4倍～6倍風屏障高度之內[21]。考慮到橋面寬度較寬，且有可能設置高度較高的半封閉聲屏障，因此本文將不同透風率下的風屏障高度的研究范圍確定為區間[2 m,5 m]。

在本研究中將障條之間空隙的總長度與風屏障高度的比值，定義為透風率。在具體設置計算工況時，按均勻抽樣的原則即取風屏障高度分別為2.0 m、3.0 m、4.0 m、5.0 m，透風率分別為0%、15%、30%、45%、60%、70%，進行兩兩組合，共計24個工況，進行了初步計算。但在建立代理模型的過程中發現：在部分區間，模型的效果較差。雖然可以采用自適應抽樣等策略[22]，但需要對每個樣本進行計算，考慮到本文二維模型計算較快，因此直接在間隔較大的區域增加了樣本點。

上述前后兩組工況共同組成了本研究的樣本，共計42個工況，如表1所示。每個工況均監測6個車道的風速分布，鑒于橋梁上通行車輛的高度分布情況，在各車道高度方向等間距0.25 m設置20個風速監控點，總高5 m。

表1 計算工況

需要注意的是：本文只探討風屏障的高度和透風率參數對扁平鋼箱梁上不同車道位置上風速折減效果的聯合影響，對于主梁上附加風屏障的幾何參數對主梁顫振和渦振等風致振動性能的影響還需做進一步的試驗和數值模擬研究。

1.3 建模方法驗證

為了考察本研究中CFD建模方法的合理性，選取某實橋風屏障，如圖4所示。用和本研究相同的方法建模，網格劃分如圖5所示。計算得到風屏障的阻力系數，和該風屏障風洞試驗測定的阻力系數進行對比，結果如表2所示。

圖4 建模方法驗證工況幾何模型(m)

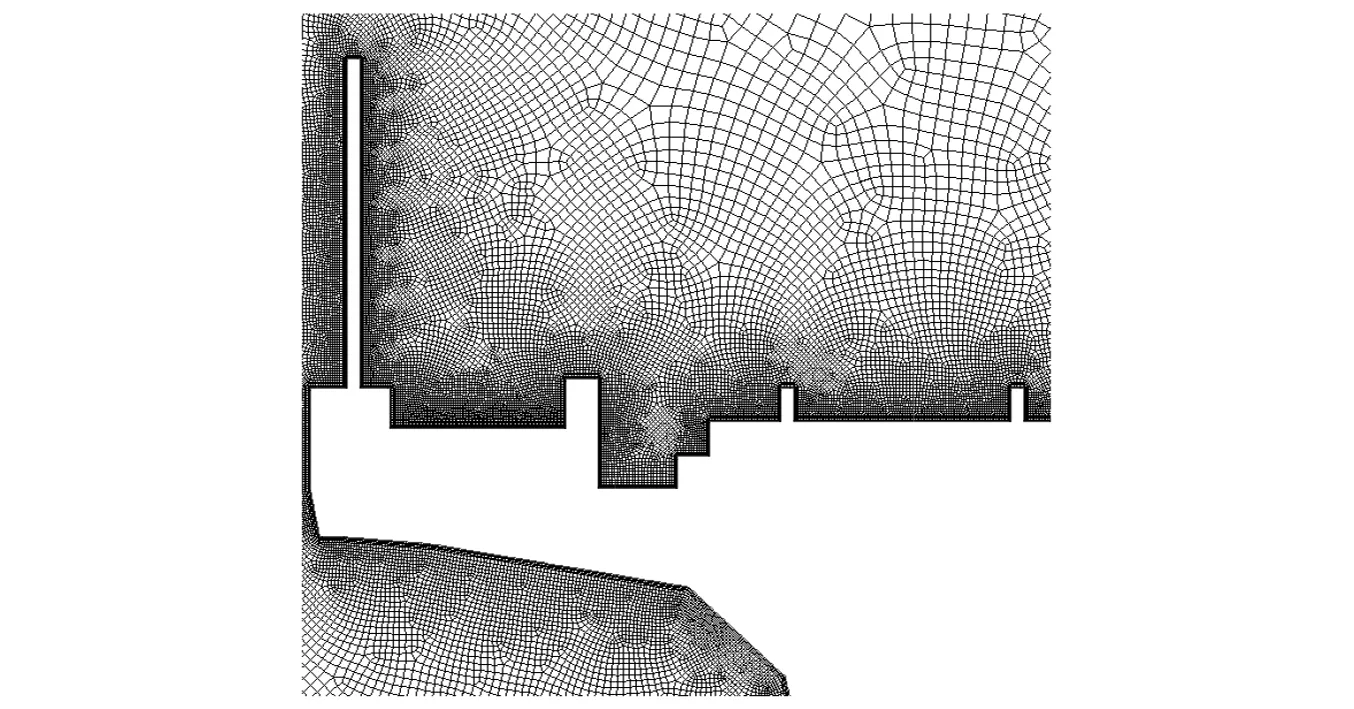
圖5 建模方法驗證工況網格劃分(局部)

表2 2 m高度風屏障氣動力模擬值與風洞試驗對比

由表2可見，本研究計算得到的阻力系數與風洞試驗值較為吻合。為進一步對比分析流場特性，給出了數值模擬和風洞試驗中得到的迎風側軌道中心的靜壓分布曲線如圖6所示。由圖6可見，數值模擬值與風洞試驗結果吻合較好。雖然驗證模型的幾何形狀與本研究中有所不同，但計算參數與劃分網格的方法是一致的，這表明本研究中所采用的湍流模型、分析參數、計算區域和網格劃分方式是可行的。

圖6 迎風側軌道中心的靜壓分布曲線與風洞試驗結果對比

考慮到驗證模型的梁截面和本文扁平鋼箱梁(見圖1)有一定的差異，因此按上述網格劃分方法、湍流模型、邊界條件和計算參數，選取風屏障透風率30%、高度3 m的工況進行網格無關性檢驗。分別針對網格數量為15.7萬、32.3萬和100.5萬的計算模型，計算得到主梁阻力系數如表3所示。由表3可見，網格數量增加到一定程度后，對主梁氣動力系數影響已較小，這表明本研究中采用的網格劃分方式是合理的，采用32.3萬左右的網格數量進行計算是可行的。

表3 網格無關性檢驗

2 風速折減系數

本文采用風速折減系數評價風屏障的防風效果。考慮到大風災害天氣造成的行車安全事故多以車輛側翻為主[1]，因此采用基于合力矩相等原則的橋面等效風速Ueff，定義[24]如下

(1)

進一步，定義風速折減系數λeff如下

(2)

式中：Zr為沿橋面向上監控風速高度的區間長度，考慮公路限界高度一般為5.0 m，本研究中風速監控點位置在橋面各車道中心線向上隔0.25 m等間距設置，具體為[0.25,0.50,…, 4.75,5.00]，考慮到離地風速通常較小，且車輛一般有一定的離地高度，因此取Zr為5 m、Z0為0.25 m，即從離地0.25 m開始計算；u為風速沿高度的分布函數；z為距離橋面的高度；U∞為均勻來流等效風速，按式(1)計算，得U∞=30 m/s。

風屏障的風速折減系數應為安裝風屏障后橋面處的等效風速與未安裝風屏障時橋面處的等效風速的比值。經過計算，未安裝風屏障時橋面處的等效風速，其和相應的U∞差別很小，分別相差：一車道，4.11%；二車道，3.59%；三車道，3.46%；四車道，2.48%；五車道，1.43%；六車道，0.59%；基于此，考慮使用方便，風速折減系數仍采用式(2)定義。

3 神經網絡模型

代理模型是指在分析和優化設計過程中可替代那些比較復雜和費時的數值分析的近似數學模型，也稱為響應面模型、近似模型或元模型[25]。代理模型方法不僅可大大提高優化設計效率，而且可降低優化難度，并有利于濾除數值噪聲和實現并行優化設計[26]。

建立代理模型的主要方法有：多項式響應面，Kriging模型，徑向基函數，人工神經網絡(artificial neural networks，ANN)，支持向量回歸(SVR)，多變量插值和回歸和多項式混沌展開等[26]。本研究采用人工神經網絡方法建立代理模型。

人工神經網絡(ANN)，是一種模仿人類神經網絡行為特征進行分布式并行信息處理的數學模型。其主要考慮網絡連接的拓撲結構、神經元特征和學習規則等[27]。

本研究直接采用MATLAB R2017a中的Neural Fitting app來建立代理模型。總樣本數為42，采用簡單隨機抽樣方法，將總樣本分成：訓練樣本、驗證樣本和測試樣本。訓練樣本是在訓練過程中用于網絡的建立，并根據其誤差對網絡進行調整。驗證樣本用于測量網絡的泛化性能，并在泛化停止改善時停止訓練。測試樣本用于在訓練期間和之后進行獨立的網絡性能測量，其對訓練沒有影響。

考慮到樣本總數量、模型的精度和測試結果的代表性，必須要有足夠的訓練樣本來建立模型，足夠的樣本作為測試樣本來檢驗模型。權衡二者，取訓練樣本數為30，占比70%，驗證樣本數為6，占比15%，測試樣本數為6，占比15%。

經過反復調試，隱藏神經元數目取為20。神經網絡結構如圖7所示。

圖7 神經網絡模型結構

由于樣本數相對較小，且用Fluent計算的風速結果有一定的隨機噪聲，計算等效風速時采用梯形數值積分有一定的誤差，故訓練算法采用Bayesian Regularization，其特點是：通常需要更多的時間，但是對于困難的、數量小的或有噪聲的數據集，可以產生良好的泛化效果，其根據自適應權重最小化(正則化)停止訓練[28]。

4 風屏障防風效果分析

4.1 風場分布

根據設置在橋面的監控點風速，選取風屏障透風率30%、高度2 m的工況，各車道的風剖面如圖8所示。

圖8 30%透風率2 m高風屏障下各車道風剖面

由圖8可知，各車道風剖面可大致分為：減風效果內的低風速區域、中間過渡區域和減風效果外的高風速區域。將6個車道分成：車道一、車道二和車道三為迎風側車道;車道四、車道五和車道六為背風側車道，分別加以討論。迎風側的車道位置處風剖面和背風側的車道位置處風剖面具有不同的變化趨勢，這可能是由于迎風側車道離風屏障較近，受其遮擋較大，在距離橋面較近位置發生了回流。

對于迎風側車道，隨著距離橋面高度的增加風速先逐步減小以致負風速，在超過1.5 m之后，風速隨距離橋面高度近似直線增加，在4.5 m之后，曲線逐步走向豎直，風速基本穩定在來流風速30 m/s附近。

對于背風側車道，風剖面曲線十分靠近，隨著高度增加，風速呈指數或二次曲線形式增長，風剖面曲線近似對數曲線或1/2次曲線，這和定性的理論分析基本一致。

4.2 風速折系數的神經網絡模型

根據各車道位置處的風速分布，按照式(1)和式(2)計算相應的風速折減系數。基于這些樣本數據，建立各車道風速折減系數的神經網絡模型。以車道二風速折減系數神經網絡模型為例，回歸結果如圖9所示。圖9中，數據點做了歸一化處理，各模型的均方誤差均小于0.001，R均大于0.97。由于網格采用size function自動劃分，導致不同工況的網格模型會有一定的差異，導致數值模擬結果中附加了一定的隨機噪聲，但代理模型可很好地反映風速折減系數的變化規律。

圖9 車道二風速折減系數神經網絡模型回歸效果

基于建立的神經網絡模型，繪制各車道的風速折減系數隨風屏障透風率和高度變化曲面如圖10所示。由圖10可知，不同車道風速折減系數隨風屏障透風率、高度參數的變化關系各不相同，沒有統一的趨勢和規律，無法簡單地用數學解析表達式來描述。基于上述神經網絡模型，可方便的預測任意高度和任意透風率組合下的風屏障在不同車道位置處的風速折減系數，有效地評估和優化風屏障的防風效果。

4.3 風屏障高度的影響

基于圖10中已經建立的各車道風速折減系數代理模型，通過控制變量的方法，來研究風屏障高度對風屏障防風效果的影響，明確定性的變化趨勢。取風屏障透風率分別為0%、15%、30%、45%和60%，風速折減系數隨風屏障高度變化曲線如圖11所示。

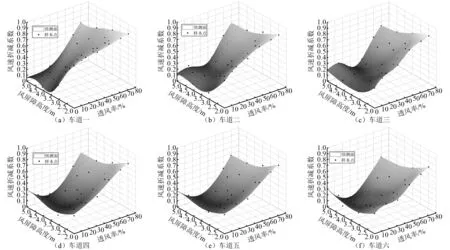
圖10 風速折減系數-屏障透風率-屏障高度

圖11 風速折減系數v.s.風屏障高度

由圖11可知，不同車道風速折減系數隨風障高度的變化趨勢具有相同的規律。不同透風率下風速折減系數隨風障高度的變化趨勢也具有相同的規律。風速折減系數隨風障高度增加，先快速減小，而后小幅度回升，之后漸漸走平，隨著透風率增加，回升幅度減小。因此，當風屏障高度增加到一定程度后，再增加高度，防風效果不會有明顯提高，由此可確定較為有利的風屏障高度。

各車道風速折減系數的大小關系大致是：車道一>車道二>車道三>車道四>車道五>車道六，特別是在透風率大于30%之后，其嚴格成立。另外，在透風率大于等于30%之后，各車道風屏障風速折減系數與風屏障高度關系曲線近乎平行，呈二次拋物線下降趨勢，且隨著透風率的增加，下降斜率變緩。

4.4 風屏障透風率的影響

與研究高度對各車道風速折減系數的影響類似，取風屏障高度分別為2.0 m、2.5 m、3.0 m和3.5 m的情況，基于建立的各車道風速折減系數神經網絡模型，計算不同透風率下風速折減系數的預測值，得到各車道風速折減系數隨風屏障透風率變化曲線如圖12所示。

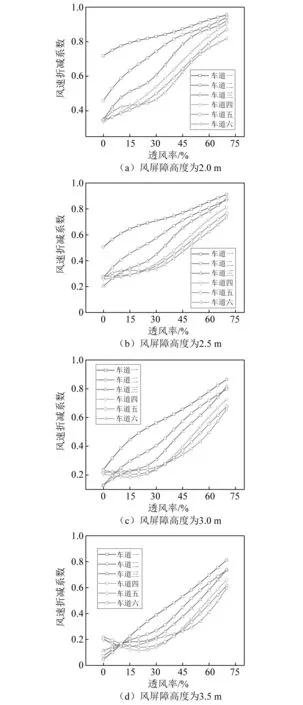
圖12 風速折減系數v.s.風屏障透風率

由圖12可知，隨著透風率的增加，各車道風速折減系數總體是上升趨勢，迎風側車道和背風側車道處曲線呈現不同的形態。

曲線在迎風側車道位置處隨著透風率的增加，從始至終呈上升態勢。在透風率小于30%時，曲線在背風側車道位置處局部有下降，漸漸走平之后，近乎二次拋物線上升，且隨著風屏障高度的增加上升段愈陡峭。另外，各車道上升段大致平行，風速折減系數的大小關系是：車道一>車道二>車道三>車道四>車道五>車道六。

4.5 風屏障防風效果的等值線

由4.3節和4.4節的分析可知，車道一的風速折減系數相對其他車道較大，對評價風屏障的風速折減效果起控制作用。因此基于4.2節建立的風速折減系數代理模型，繪制車道一風速折減系數等值線圖。由于在大跨度橋梁上通常只需把風速降低到跟在路基上一樣即可，因此提取折減系數λ為0.3、0.4和0.5的等值線數據點，采用4階多項式進行擬合，如圖13所示。

圖13 風速折減系數等值線(車道一)

風速折減系數λ=0.3時，風屏障透風率p和高度h的擬合公式為p=6.229h4-98.92h3+572.4h2-1 405h+1 233；風速折減系數λ=0.4時，風屏障透風率p和高度h的擬合公式為p=5.413h4-84.09h3+471.6h2-1 103h+908.1；風速折減系數λ=0.5時，風屏障透風率p和高度h的擬合公式為p=4.321h4-64.09h3+337.5h2-715.8h+511。上述擬合的R-square均在0.99以上，擬合效果良好。

通過擬合公式，在確定了風速折減系數的前提下，確定風屏障高度后，可簡便地定出風屏障的透風率參數，可為風屏障的設計提供一定的參考。

5 結 論

通過數值分析，研究了扁平鋼箱梁上風屏障的防風效果，討論了設置風屏障后橋面的風場分布，基于代理模型建立了風屏障風速折減率與風屏障高度和透風率的代理模型，研究了風屏障高度和透風率的影響，分析了風屏障防風效果的等值線，得出如下結論：

(1)各車道風速折減系數和風屏障透風率、高度參數的函數關系較為復雜，無法用解析表達式來描述，可以基于試驗樣本和數值模擬樣本用本文的方法建立代理模型，預測在主梁上安裝任意高度和任意透風率組合下的風屏障時不同車道位置處的風速折減系數，評估風屏障的防風效果，對風屏障的設計提供一定的參考。

(2)風速折減系數隨風屏障高度增加，先快速減小，之后漸漸走平。因此，當風屏障高度增加到一定程度后，再增加高度，防風效果不會有明顯改善，基于此可以確定較為有利的風屏障高度。

(3)風速折減系數隨風屏障透風率的增加，曲線在迎風側車道和背風側車道位置處呈現不同的形態。在迎風側車道位置處，曲線從始至終呈上升態勢；在背風側車道位置處局部有下降，漸漸走平之后，再上揚。

(4)在風屏障透風率大于20%，高度小于3.5 m的情況下，各車道風速折減系數的大小關系比較統一，依次是：車道一>車道二>車道三>車道四>車道五>車道六，這時車道一的風速折減系數對評價風屏障的防風效果起控制作用。