“x=5”是不是方程？

周佳泉

【編者按】 數(shù)學(xué)是嚴(yán)謹(jǐn)?shù)目茖W(xué)。在大部分人的心目中，數(shù)學(xué)“一是一，二是二”。但在實(shí)際的教學(xué)中，我們常常遇到一些數(shù)學(xué)問(wèn)題似乎難有定論。從本期開(kāi)始，我們將開(kāi)辟“牛角尖里的數(shù)學(xué)”專欄，選取一線教師們普遍關(guān)心的“有爭(zhēng)議”的問(wèn)題，為大家提供一個(gè)交流、借鑒的平臺(tái)，以期對(duì)小學(xué)數(shù)學(xué)教學(xué)中“有爭(zhēng)議”的問(wèn)題達(dá)成一個(gè)比較清晰的共識(shí)，也歡迎大家提問(wèn)共討。

“x=5”是不是方程？這是一線教師們經(jīng)常爭(zhēng)論的一個(gè)問(wèn)題。本人認(rèn)為，對(duì)這個(gè)問(wèn)題要進(jìn)行分類討論：

一、從方程的文字定義來(lái)說(shuō)

根據(jù)現(xiàn)行人教版小學(xué)數(shù)學(xué)教材對(duì)方程的文字定義“含有未知數(shù)的等式，叫作方程”來(lái)說(shuō)，“x=5”絕對(duì)算是一個(gè)方程。因?yàn)樗戏匠潭x的兩個(gè)要素——首先它是等式，其次含有未知數(shù)“x”。

二、從方程的功能價(jià)值來(lái)說(shuō)

如果基于“方程是在未知量與已知量之間建立等量關(guān)系，從而求得問(wèn)題解決的一種思維工具”的功能價(jià)值來(lái)說(shuō)，“x=5”算不上是一個(gè)真正的方程。原因有兩個(gè)：一是這個(gè)方程沒(méi)有任何實(shí)用價(jià)值（它不能解決任何實(shí)際問(wèn)題）;二是未知數(shù)“x”的值已經(jīng)確定（就是5），“x”已經(jīng)不是真正的未知數(shù)了（這就好比甲問(wèn)乙：“張老師，請(qǐng)問(wèn)您貴姓？”）。

三、從解析幾何的表達(dá)式來(lái)說(shuō)

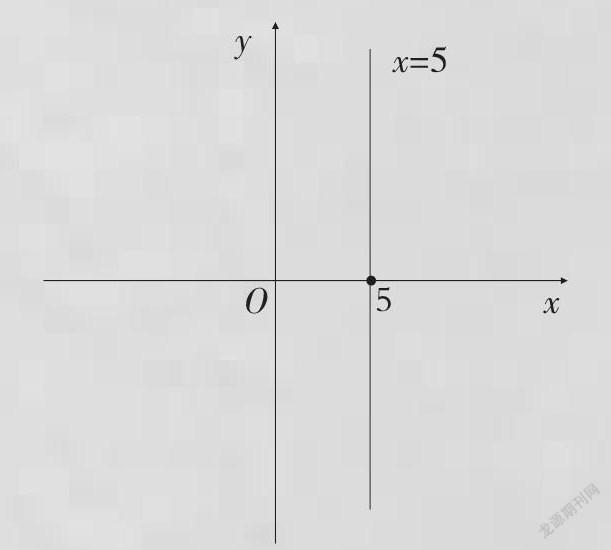
如果從解析幾何的表達(dá)式來(lái)說(shuō)，“x=5”確確實(shí)實(shí)是一個(gè)方程。它描述的是在平面直角坐標(biāo)系中通過(guò)“x=5”這個(gè)點(diǎn)，并且平行于軸的直線（如下圖）。

啟示：

1.思考問(wèn)題從目標(biāo)切入才更有價(jià)值。比如我們討論“‘x=5’是不是方程？”這個(gè)問(wèn)題之前，恐怕我們更應(yīng)該先反問(wèn)自己：“判斷‘x=5’是不是方程，我們的目的是什么？”

2.摒棄二元思維才能對(duì)問(wèn)題達(dá)到全面理解。長(zhǎng)期從事一線小學(xué)數(shù)學(xué)教學(xué)的工作，容易讓人形成“嚴(yán)謹(jǐn)有余，變通不足”的思維定式，尤其容易落入“非此即彼，不對(duì)就錯(cuò)”的二元思維窠臼之中。“分類討論”是消除二元思維局限性的良好思維方法，值得我們大家借鑒。