立足課標 回歸教材 提升素養
——以一道學業水平題為例

浙江省嘉興市秀洲區王店鎮建設中學 (314011) 洪 安浙江省海寧市丁橋中學 (314400) 陳振鋒

一、試題呈現與評價

(一)原題呈現

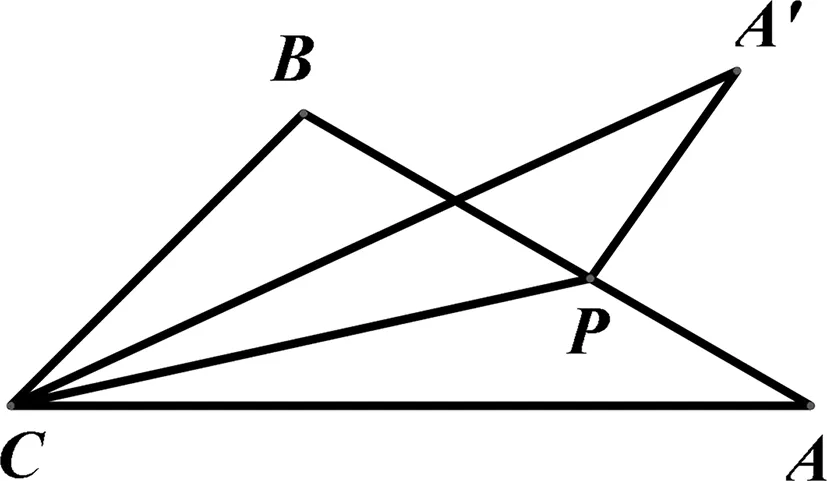
圖1

如圖1，在△ABC中， ∠BAC=30°,∠ACB=45°,AB=2,點P從點A出發沿AB方向運動,到達點B時停止運動.連接CP，點A關于直線CP的對稱點為A′，連接A′C，A′P.在運動過程中，點A′到直線AB距離的最大值是；點P到達點B時，線段A′P掃過的面積為.

(二)試題評價

1.動靜結合，圖形美觀

本題的三角形是一個內角為30度和45度的鈍角三角形，在初中階段，學生對于這兩個角度非常熟悉，在考場上看到這樣的角度和圖形，學生會有親切感.當我們過點B做AC的垂線后，就分割成了兩個非常熟悉的直角三角形，從而已知一邊，可以快速求出其他線段的長度.平時學習過程中，要多關注特殊的基本圖形，學會欣賞圖形的美妙之處.

P是線段AB上的一個動點，點A關于直線CP的對稱點為A′，圖形的軸對稱變換是一種非常美觀的構圖方式.題中的構圖方式，有動有靜，動靜結合.學生能在這個變化中找到動和靜，變與不變，將為解題帶來思路.整個圖形線條簡潔，構圖直觀，清晰美觀，讓學生體會幾何圖形獨特的美感.

2.線面結合，題目簡潔

本題是2021年浙江省嘉興市初中數學學業水平考試填空題的最后一題，兩小問，共4分，問題簡潔，兩小問具有遞進關系，分別求的是點到直線的距離和線段掃過的面積.點動到線動，線動又可以進一步求解面積，這是我們平時學習的流程，從學生的最近發展區出發，為通過動點來發展教學內容，提供了教學材料，讓學生經歷知識的發展建構過程，這為我們平時的教學提供了思路.這樣的教學流程，必然能提升學生的直觀想象、邏輯推理、數學運算等核心素養.

二、試題求解

(一)重視審題，獲取思路

審題是解題的第一步，從審題的過程中獲取多少信息，產生多少知識間的聯想，將直接影響到題目的解決.在△ABC中，∠BAC=30°,∠ACB=45°,AB=2,直接可以得到另外兩邊的長度.點A關于直線CP的對稱點為A′，可以得到△ACP?△A′CP，P在動的過程中，線段A′C=AC，根據動點到定點的距離等于定長，可以知道A′的軌跡是一條弧，這為我們后續的解題提供了方向.第一問要求A′到直線AB距離的最大值，可以聯想到垂徑定理，即A′C垂直于直線AB時，所求距離最大.第二問要求線段A′P掃過的面積，我們已經確定A′的軌跡是一條弧，從而可以確定所求面積是圓心角為90度扇形的一部分，通過對P點特殊位置——起始點和終點的作圖，可以確定圖形，從而求解.

(二)重視畫圖，以靜制動

解決幾何題，特別是動點軌跡問題，作圖是關鍵，可以幫助思考，輔助計算.在動點問題中，要學會以靜制動，根據題目條件的特點，作出符合題意的圖形，通過對圖形的直觀分析、判斷，以此來進一步求解.本題中學生一定要嘗試大膽作圖，現將輔助圖形呈現如下：

第一問輔助圖(見圖2，圖3，圖4)：

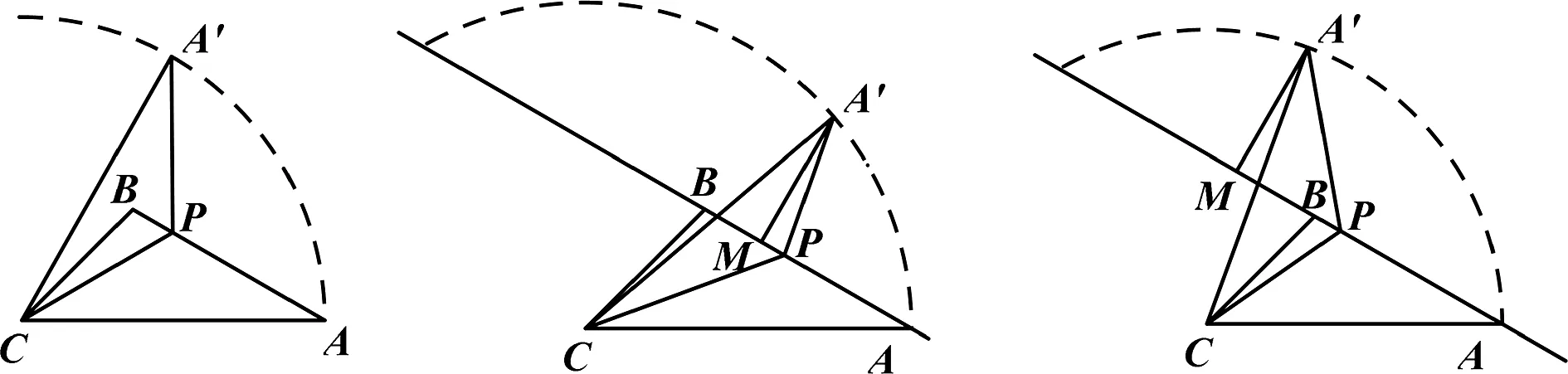
圖2 圖3 圖4

第二問輔助圖(見圖5，圖6)：

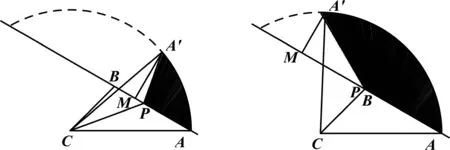
圖5 圖6

有了圖形就能獲得直觀的感受，從而突破本題帶來的困擾.通過對圖形的分析和計算，就能獲得答案.作圖是一個呈現思維的過程，讓思維可視化，也讓教師進一步了解學生的知識掌握情況和思維發展情況.精準作圖，助力輕松解題.

(三)重視計算，獲得答案

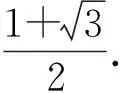
三、深度挖掘

(一)再探基本圖形

本題的基本圖形是一個45度和30度的鈍角三角形，對于此圖形課本中涉及較少，能不能基于兩個特殊角，利用該圖形得到一些常用的結論，成了筆者在解決此題后思考的第一個問題.

基本圖形7，過點B做AC的垂線，分割成兩個特殊的直角三角形，這兩個直角三角形在平時的課堂中研究較多，三邊的關系比較清楚，故在本文中，不再多加敘述.

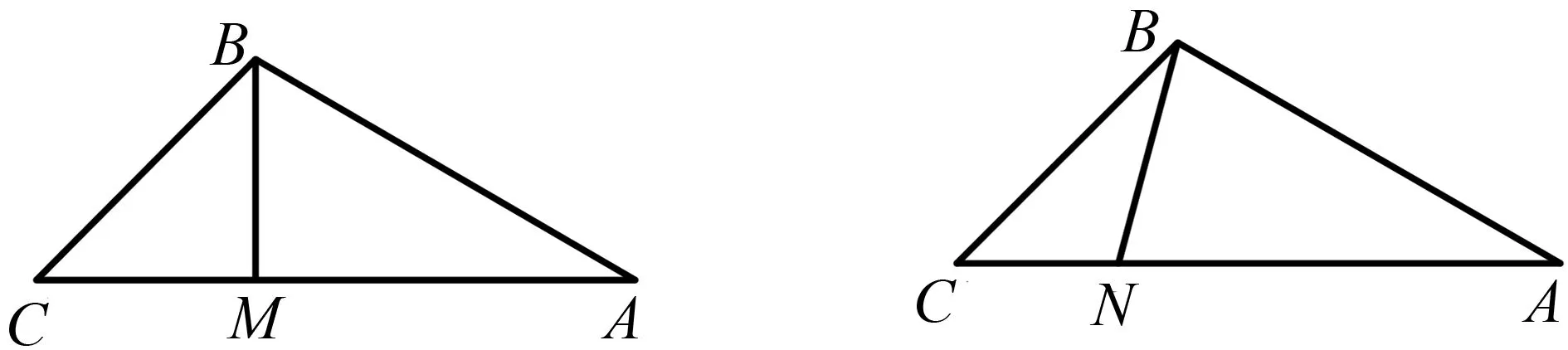
圖7 圖8

圖形8，作AN=AB，將△ABC分割成一個頂角為30度的等腰三角形，則另一個三角形與它本身相似，此處，我們可以進一步探究頂角為30度角等腰三角形模型的三邊關系.

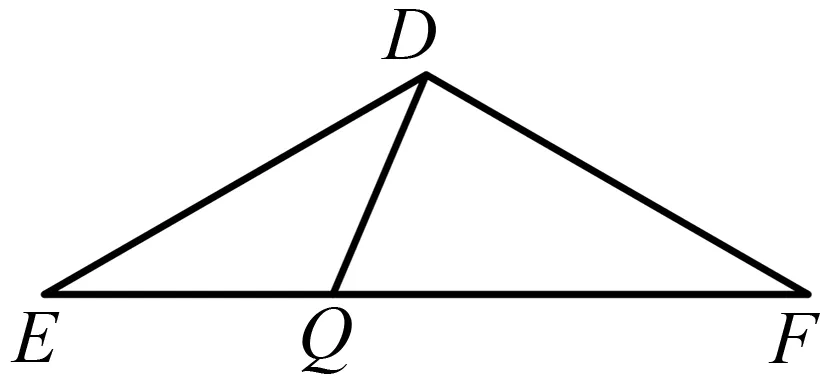
圖9

圖形9，在一個頂角為120度的等腰三角形中，作FD=FQ，得到一個頂角為30度的等腰三角形和一個內角為30度和45度的三角形，即△ABC～△EQD,從等腰三角形DEF的邊角關系可以進一步探究分割出的三角形邊的關系.

(二)再作圖形變換

本題的圖形變化是軸對稱變換，還可以研究圖形的平移和旋轉，在此將進一步通過圖形旋轉，探索在這個過程中，得到的一些結論，也啟發學生在平時的學習中，學會多角度的看待問題，探究問題，總結問題.

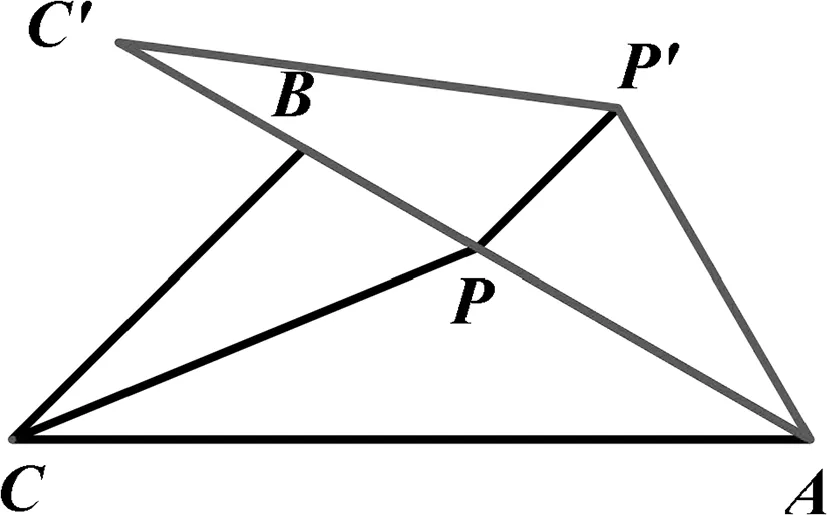
圖10

變式1 如圖10，在△ABC中，∠BAC=30°,∠ACB=45°,AB=2,點P從點A出發沿AB方向運動,到達點B時停止運動.連接CP, 將△ACP繞著點A順時針旋轉30°得到△AC′P′.設AP的長度為t，求：(1)PP′的長度(用t表示)；(2)求△PC′P′面積的最大值.

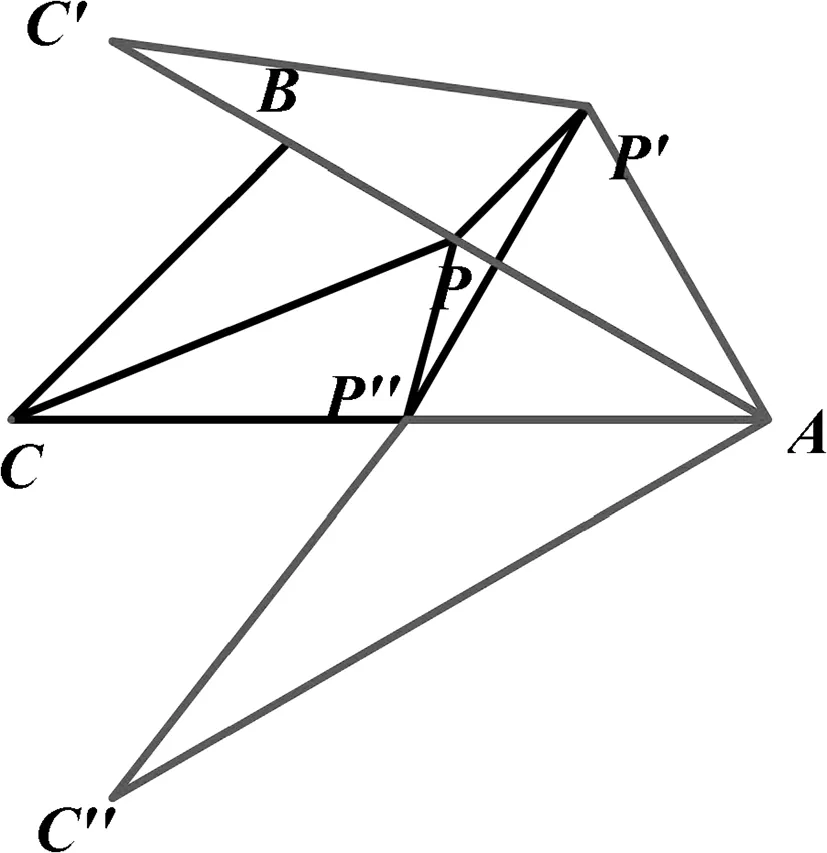
圖11

變式2 如圖11，在△ABC中，∠BAC=30°, ∠ACB=45°,AB=2,點P從點A出發沿AB方向運動,到達點B時停止運動.連接CP，將△ACP繞著點A順時針旋轉和逆時針都旋轉30°得到△AC′P′和△AC″P″.設AP的長度為t，求：

(1)∠P′PP″的度數是否為定值，若為定值，求出其度數；

(2)求△P′PP″的面積(用t表示)；

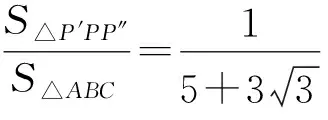
(三)再求變式結論

在有了兩個變式之后，可以嘗試去計算結果，培養空間觀念、運算能力和模型思想.

在求解的過程中，學生綜合運用了各種知識，對題目有了更深刻的認識，提高了個人的數學素養，培養了探究精神.

四、教學思考

(一)關注課標，挖掘教材

《義務教育數學課程標準(2011年版)》指出：“教師教學應該以學生的認知發展水平和已有的經驗為基礎，面向全體學生.”本題的背景源于課本，但是又高于課本.教材中對于特殊的直角三角形都有所涉及，但是組合型的三角形又沒有直接呈現，啟發我們在教學過程中多探索新的特殊圖形.《課標》中對圖形的軸對稱提出了明確的要求，而本題是在動態中的軸對稱，相比于以往的題目，難度有所增加，但是考查的知識點又都是我們所熟悉的.如何利用課本，又能讓學生挖掘出高于課本的素材，需要教師不斷的引導，師生共同的探索.

(二)關注方法，抽象模型

數學的練習，要做一題，會一類，這就需要在每道題后及時反思和總結方法.如對于本題來說，首先如何解決軌跡問題值得反思，初中階段，軌跡一般分為兩類，線段和弧.本題中確定軌跡為弧后，考慮利用割補法解決問題.其次遇到點到直線的距離問題如何思考，結合A′的軌跡為弧，轉化到了垂徑定理，從而解決問題.我們也可以把上述的兩種思考，提煉出兩種模型，遇到相似的問題時，就往這樣的角度去思考.在平時的教學過程中，我們要多引導學生對圖形進行探究，通過歸納反思，提煉模型，培養模型意識.

(三)關注思想，提升素養

數學思想蘊含在數學知識形成、發展和應用的過程中，是數學知識和方法在更高層次上的抽象與概括.而數學活動經驗的積累是提升數學核心素養的手段，這是師生積極參與、交往互動、共同發展的過程.在本題的解決過程中，學生的數感、空間觀念、幾何直觀、推理能力、運算能力與模型能力等得到進一步的提升.學生需要通過分析題意，利用幾何直觀構建圖形，在此過程中學生的作圖能力得到進一步發展.通過題意，利用所學，充分利用已知的模型，將復雜的問題進行轉化.這一過程中，學生也充分體會到了數形結合、轉化等數學思想對于解題的幫助.在平時的教學過程中，教師要強調幾何直觀和模型思想的重要性，要善于引導學生總結模型，聯想模型，應用模型.教師只有在平時的課堂中不斷的滲透數學思想方法，學生才能在學習活動中感知核心素養，從而提升個人的數學素養.