兩道圓錐曲線題的思考與結論推廣

安徽省碭山中學 (235300) 蔡 聰

文[1]以2020年高考數學全國卷Ⅰ理科第20題和2020年高考數學山東卷第22題為例，介紹了齊次化方法在解決圓錐曲線中關于斜率之和為定值或斜率之積為定值的問題中的應用，并歸納了齊次化方法解題的步驟，可操作性強.經過筆者思考，借助于齊次化方法將兩道題的結果推廣到一般的情況，探究如下：

一 問題探究及結論推廣

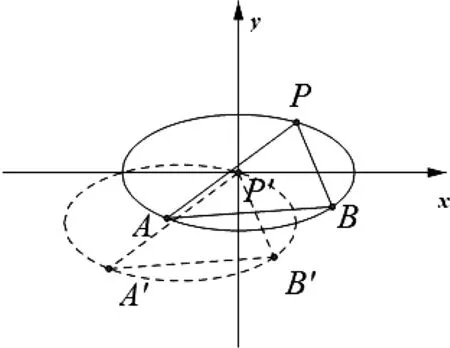
圖1

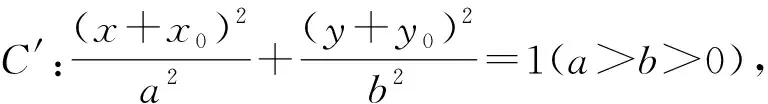
上面的分析過程亦證明了下面結論成立：

評注：通過聯立橢圓與直線方程，構造齊次方程A(y-y0)2+B(y-y0)(x-x0)+C(x-x0)2=0，證明了當直線PA與PB的斜率之和為定值時，隨λ取值不同，直線AB存在定點或定值的情況.以該結論為背景的高考題還有2017年高考數學全國1卷理科第20題.故對高考題，不能僅僅解答出來就滿足了，還應充分利用歸納與類比的思想，將結論推廣，體會數學發現的過程.

對于斜率之積為定值，是否有類似的結論？

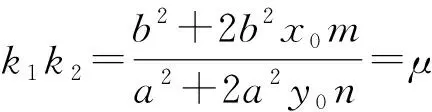
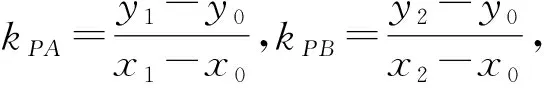
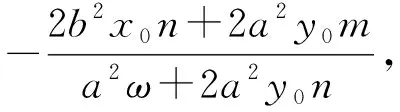
評注：2015年高考數學陜西卷文科第20題所考查的便是此結論的特殊情況.

同樣地，若直線AB斜率為定值，也可以得到如下結論：

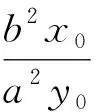
二 關于圓錐曲線高考備考的一點思考

1 加強方法訓練，提高應用意識

對于斜率和為定值或積為定值的圓錐曲線模型，相較于常規解法(聯立消元，韋達定理)，齊次化方法的步驟簡潔，計算量少.教師在教學時，不應開門見山，而是通過比較兩種方法的優缺，讓學生去接受、練習和掌握.

2 挖掘試題背景，培養必備能力

數學家波利亞說“數學問題的解決僅僅只是一半，更重要的是解題之后回顧”，他把解題作為培養學生數學才能和教會學生思考的一種手段與途徑.這種訓練不同于單純的題海戰術，而是選取一個有意義又不復雜的題目，幫助學生深入挖掘試題的各個側面，使學生通過這個題目，觸類旁通，獲得解題的一般思考方式.尤其是高考題這個寶藏，學習過程中，應不僅限于解題，更要剖析問題背景，對結論進行拓展，延伸，尋找特殊情境下的一般規律，這樣學生才能在解題過程中提高發現和提出問題的能力、分析和解決問題的能力.

3 關注問題本質，發展核心素養

很多學生在處理圓錐曲線問題時，往往會出現有思路，但是計算受阻，或者計算得不到想要的結果，這是由于運算素養的缺失所造成的，《普通高中數學課程標準(2017年版2020年修訂)》提出了數學的六大核心素養，其中數學運算既基礎又重要，教師應在觀察式子結構，明確計算方向，選擇計算方法，有效化簡，徹底化簡等方面做足功課，在以后的教學中，應鼓勵學生增強信心，不怕困難，勇于攻堅克難.