KKM定理中無限交集的緊性及其應(yīng)用
王元恒, 李雪婷
(浙江師范大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院,浙江 金華 321004)
0 引 言
著名的KKM定理是現(xiàn)代非線性分析中最重要的定理之一,由Knaster等[1]3位波蘭數(shù)學(xué)家于1929年在有限維空間RN中建立的.KKM定理為數(shù)學(xué)科學(xué)不同領(lǐng)域的許多現(xiàn)代重要成果奠定了基礎(chǔ).Nash[2]利用KKM定理導(dǎo)出的不動點定理證明了有限個非合作博弈中均衡點的存在性,創(chuàng)立了均衡理論而獲得了諾貝爾經(jīng)濟學(xué)獎.1961年,Fan[3]把KKM定理推廣到無限維空間并給出了極大極小不等式定理.
定理1[3]設(shè)X是拓撲向量空間Y中的任意集合.對于每個x∈X,設(shè)Y中的閉集F(x)滿足以下2個條件:
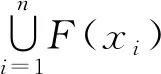
2)至少存在一個x∈X,使得F(x)是緊的.
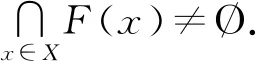
近年來,人們從許多方面改進和推廣了KKM定理,在 KKM 定理及其均衡理論、極小極大的理論和應(yīng)用方面取得了很大的進展[4-15].例如,把KKM定理中的空間改進為無限維Hausdorff線性拓撲空間、超凸空間、H-空間、G-凸空間等;把KKM定理中的閉集改進為凸閉集、集的閉包是閉的、集是有限閉、轉(zhuǎn)移閉等.但是,對于KKM定理中無限交集的結(jié)構(gòu)研究并不多,包括其交集的唯一性、閉性、凸性、緊性等.本文在原有條件不變的情況下,研究了KKM 定理中無限交集的結(jié)構(gòu)問題,證明了KKM定理中的無限交集不但非空,而且還是閉集、緊集,同時還給出了KKM定理中的一些交集結(jié)構(gòu);推廣了著名的Minty引理,并在此基礎(chǔ)上,結(jié)合本文給出的KKM定理中交集結(jié)構(gòu),證明了抽象變分不等式解集的緊性、凸緊性定理和解的存在唯一性定理.本文的結(jié)果推廣和改進了許多已有的相關(guān)結(jié)果.
1 KKM定理中交集的緊性
首先在原來條件不變的情況下,從理論上給出KKM定理中交集的閉性、緊性證明.
定理2設(shè)X為Hausdorff線性拓撲空間E中閉凸集,F是E的任意有限維子空間.若?x∈X,?M(x)?E,滿足以下條件:
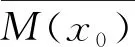

3)?x∈X,M(x)有限閉,即M(x)∩F在F中是閉集;
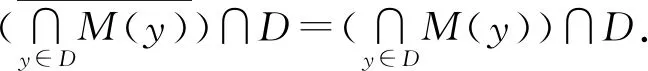
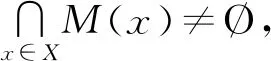
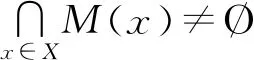
作一個新的集值映射M*:X→2X,M*(x)=M(x)∩X,?x∈X,則M*也滿足:

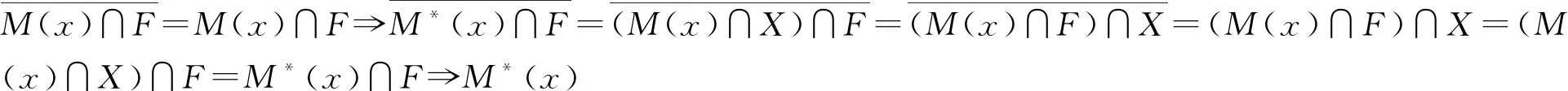
4)任意的有限維截口Dx0,有

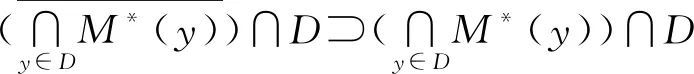
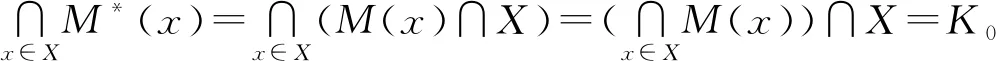
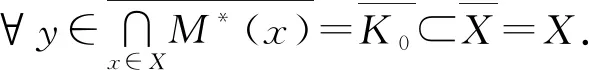

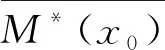
為非空緊集.定理2證畢.
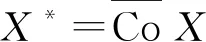
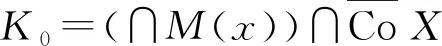
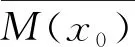
2 抽象變分不等式解集的緊性
利用定理2的KKM交集為非空緊集結(jié)構(gòu),作為應(yīng)用,可以得到下面抽象變分不等式解集的閉性、緊性.
定理3設(shè)E為Hausdorff線性拓撲空間,X為E中凸閉集,泛函f:X→(-∞,+∞],f?+∞,二元泛函φ:X×X→R1,且當x∈X時,φ(x,x)≥0.若還滿足:
1)X緊,或者存在緊K及x0∈X∩K具有強制性條件
f(x)>φ(x,x0)+f(x0), ?x∈X-K;
2)?x∈X,f(·)+φ(x,·)擬凸;
3)?y∈X,f(·)-φ(·,y)在任何有限維子空間下半連續(xù);
4)對任何有限維截口D,?xα∈X∩K,xα→x∈D,?y∈D,
f(xα)≤φ(xα,y)+f(y)?f(x)≤φ(x,y)+f(y).
則抽象變分不等式
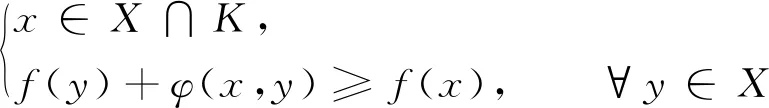
(1)

證明?y∈X,作M(y)={x∈X|f(y)+φ(x,y)≥f(x)}?X,則易驗證M:X→2X滿足定理2的全部條件[4],從而
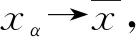
f(y)+φ(xα,y)≥f(xα), ?y∈X,
則
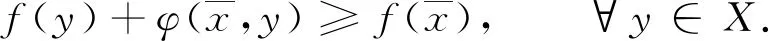
證明由于抽象變分不等式(1)的解集K0是緊集,從而K0是閉集,所以結(jié)論成立.推論1證畢.
推論2在定理3中,把條件4)換為“4′)φ(x,y)偽單調(diào)且f(x)下半連續(xù)”,其他條件不變,則抽象變分不等式(1)的解集為K∩X中的非空緊集.
證明因為由條件4′)能推出條件4)成立[4],所以結(jié)論成立.推論2證畢.
推論3在定理3中,把條件3)和條件4)合并換為“3′)?y∈X,f(·)-φ(·,y)下半連續(xù)”,其他條件不變,則抽象變分不等式(1)的解集為K∩X中的非空緊集.
證明因為?y∈X,可由條件3′)推出條件3)和條件4)成立,所以結(jié)論成立.推論3證畢.
注3與文獻[4,16]相比,定理3及推論1~推論3在條件完全相同的情況下,不僅給出了抽象變分不等式(1)的解的存在性,而且還進一步得到了抽象變分不等式(1)的解集為“非空”“閉的”“緊集”的結(jié)果.
3 Minty引理的推廣與凸性
接下來,首先推廣著名的Minty引理[17],再結(jié)合定理 3,可以得到抽象變分不等式(1)解集的凸性、緊凸性、唯一性結(jié)果,進而得出解集的結(jié)構(gòu)性定理.
定理4設(shè)E是Hausdorff線性拓撲空間,X?E為凸閉集.若
1)泛函f:X→(-∞,+∞],但不恒為+∞,下半連續(xù);
2)φ:X×X→R單調(diào)半連續(xù),?x∈X有φ(x,x)≥0;
3)?x∈X,f(·)+φ(x,·)擬凸.
則對x∈X,有下面的等價關(guān)系:
f(y)+φ(x,y)≥f(x),?y∈X??f(y)-φ(y,x)≥f(x),?y∈X.
(2)
即,若令
M(y)={x∈X|f(y)+φ(x,y)≥f(x)},
H(y)={x∈X|f(x)+φ(y,x)≤f(y)},
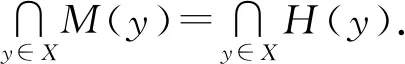
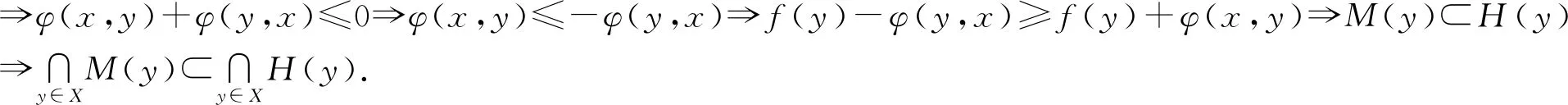
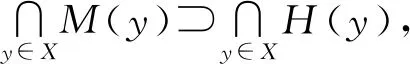
f(x)+φ(y,x)≤f(y), ?y∈X;
(3)

(4)
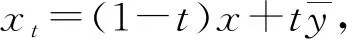
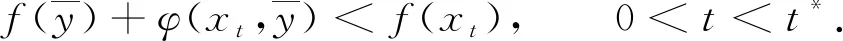
(5)
在式(3)中令y=xt,得
f(x)+φ(xt,x)≤f(xt), 0 (6) 把不等式(5)與不等式(6)作凸組合,得 再由f(·)+φ(x,·)的擬凸性得 即 f(xt)+φ(xt,xt) 由此知f(xt)<+∞,φ(xt,xt)<0,這與已知條件φ(y,y)≥0(?y∈X)矛盾.定理4證畢. 4)?x∈X,φ(x,y)對y是下半連續(xù)的. 推論4在定理4的條件下,抽象變分不等式(1)的解集為凸集(可能為空集). 定理5在定理4的條件1)、條件2)、條件3)和注4的條件4)下,抽象變分不等式(1)的解集K0?X∩K是非空凸緊集;若進一步假定φ是嚴格單調(diào),或者f(·)+φ(x,·)是嚴格擬凸,則解集K0為單點集,即得式(1)解的唯一性. 假設(shè)有x1,x2∈K0,x1≠x2,則必有 f(x2)+φ(x1,x2)≥f(x1),x2∈X; (7) f(x1)+φ(x2,x1)≥f(x2),x1∈X. (8) 因為f(x1)<+∞(否則由?y∈X,f(x1)≤φ(x1,y)+f(y)知f(y)恒為+∞,與已知條件矛盾),f(x2)<+∞,所以f(x1)+f(x2)<+∞,把式(7)和式(8)相加,得 f(x2)+f(x1)+φ(x1,x2)+φ(x2,x1)≥f(x1)+f(x2), 即 φ(x1,x2)+φ(x2,x1)≥0. (9) 由φ的單調(diào)性得 φ(x1,x2)+φ(x2,x1)≤0. (10) 當φ嚴格單調(diào)時,式(10)為嚴格不等號,結(jié)合式(9)即得0<0,矛盾;當f(·)+φ(x,·)嚴格擬凸時,式(9)為嚴格不等號,結(jié)合式(10)即得0<0,也矛盾.因此,假設(shè)不成立,即在φ嚴格單調(diào)或f(·)+φ(x,·)嚴格擬凸時,K0只能為單點集.定理5證畢. 推論5設(shè)f:X→(-∞,+∞],φ:X×X→R,f?+∞,φ單調(diào),則抽象變分不等式(1)的解集K0具有如下性質(zhì): ?x1,x2∈K0,φ(x1,x2)+φ(x2,x1)=0. (11) 證明由式(9)與式(10)即可證得結(jié)論成立.推論5證畢. 證明在式(11)中取x1=x2即可證得結(jié)論成立.推論6證畢. 推論7在定理5的條件中,僅把條件φ(x,y)的單調(diào)換成偽單調(diào),則定理5的所有結(jié)論都成立. 推論8在定理5中,把條件3)和4)合并換為“3")?y∈X,f(·)-φ(·,y)下半連續(xù)”,其他條件保持不變,則定理5的結(jié)果都成立. 推論9在定理5中,把條件3)和條件4)合并換為“3?)?y∈X,φ(·,y)上半連續(xù)”,則定理5的結(jié)論都成立. 證明因為φ(·,y)上半連續(xù),所以-φ(·,y)下半連續(xù),則由推論8即可證得結(jié)論成立.推論9證畢. 定理2在文獻[4]原有條件不變的情況下,證明了KKM定理中的無限交集不但非空,而且它還是閉集、緊集.定理4給出了著名的Minty引理[17]的推廣,因為比原來的條件少了“下半連續(xù)”,所以結(jié)果中的交集也不能保證非空,但是這一點并不影響它的廣泛應(yīng)用.定理3和定理5及其推論給出了抽象變分不等式(1)的解集里的緊性、閉性、凸性、唯一性及其特征結(jié)構(gòu).這些結(jié)果與原來已有結(jié)果相比[4-6,16,18],不但給出了變分不等式解的存在性,而且還證明了解集的緊性和條件唯一性,另外還對一些條件的對稱性及其條件要求進行了減弱和變化,特別注意的是把文獻[4,18]的條件“?x∈X,φ(x,·)下半連續(xù)”改變?yōu)闂l件“?y∈X,φ(·,y)上半連續(xù)”,說明這樣的條件在所要證的結(jié)果中是處于等價的對稱條件地位,顯示了數(shù)學(xué)結(jié)構(gòu)的內(nèi)在美.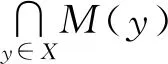


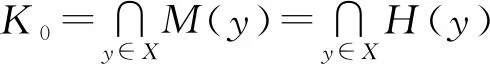

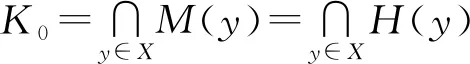
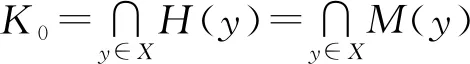
4 結(jié) 語

