基于短周期預測的感應信號控制方法研究

毛程遠， 王 琴， 錢 俊， 姜 偉， 求英浩， 楊勝德， 張欣環

(1.浙江師范大學 工學院，浙江 金華 321004;2.金華市現代物流發展管理中心，浙江 金華 321000；3.嵊州市自然資源和規劃局，浙江 嵊州 312400)

0 引 言

交叉口是城市路網通行能力的瓶頸區，是城市道路交通擁堵的關鍵節點.近年來，城市交通擁堵形勢的加劇，使得尋求更高效的交通運行方式成為城市管理的當務之急，優化交叉口信號控制方案就是最重要的方式之一.

隨著智能檢測技術的成熟，感應信號控制憑借其超強的適應性和高效的控制效率得到了越來越廣泛的應用.傳統感應信號控制各相位的綠燈時間由初始綠燈時間和單位綠燈延長時間組成，能根據車輛的到達率自動調整綠燈時間，從而提升交叉口的通行效率.美中不足的是：傳統的感應信號控制的單位綠燈延長時間是一個定值，不能適應不同車型組成和不同交通密度影響下車頭時距的變化[1]，使綠燈時間與實際通行時間需求不能動態匹配，形成不穩定的延誤[2-3].

因此，本文通過統計分析歷史信號周期與車輛到達率的數據，研判交通流車頭時距和車型組成變化趨勢，計算與之動態匹配的單位綠燈延長時間，從而優化感應信號配時方案.

1 改進的感應信號控制的理論基礎

1.1 綠燈時間的基本組成

車流通過交叉口時分3個階段，感應信號的綠燈時間也由相應的3部分組成[3]：

1)首車通行階段.此階段為排隊車流的首車從綠燈開始到該車通過停車線的時間，該階段的時間易受車型、駕駛員的反應速度等因素的影響.考慮到駕駛員的反應速度測量困難，穩定性差，實操性低，因此,本文不考慮駕駛員的反應速度對通行效率的影響.

2)飽和跟馳階段.此階段車流以飽和車頭時距通過停車線，包括2部分車輛：①紅燈時就在排隊的車輛，車輛數為qij1(單位：veh，下同)，如圖1所示；②綠燈時到達但仍受前車制約并以飽和車頭時距行駛的車輛，車輛數為qij2，如圖2所示.

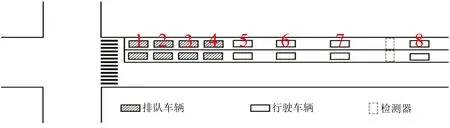
圖1 飽和跟馳階段第1部分車輛的行駛狀態

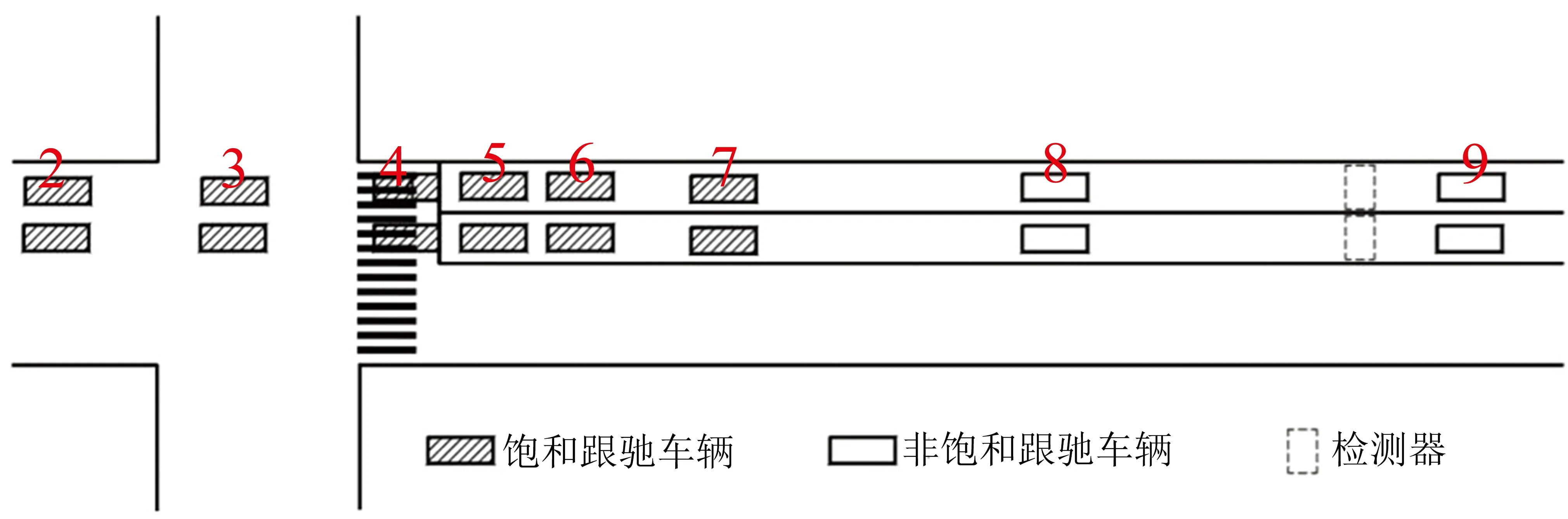
圖2 飽和跟馳階段第2部分車輛的行駛狀態

3)非飽和跟馳階段.綠燈期間到達的車輛，且與前車有較大的車頭時距，不用停車排隊就能通過停車線,該部分的車輛數為qij3.該階段結束后進入下一相位，結束原則與傳統感應信號一致[3-4].

以某交叉口為例，第j周期第i相位時關鍵車道通過的車輛數為Qij，則

Qij=q+qij1+qij2+qij3.

(1)

式(1)中：Qij為第j周期第i相位關鍵車道通行的車輛數(單位：veh，下同)；q為排隊首車車輛數(單位：veh，下同)，即q=1.

1.2 車輛組成與車頭時距分析

感應信號綠燈時間的影響因素為車輛數和車頭時距，車輛數可以由檢測器直接檢測得到，而車頭時距與車型組成有密切關系.前后車輛之間的車型組成有以下4種情況：

1)前面小型車+后面小型車，車型組成以s+s表示，車頭時距以Hss表示(單位：s，下同)；

2)前面小型車+后面大型車，車型組成以s+h表示，車頭時距以Hsh表示；

3)前面大型車+后面小型車，車型組成以h+s表示，車頭時距以Hhs表示；

4)前面大型車+后面大型車，車型組成以h+h表示，車頭時距以Hhh表示.

車型組成與車頭時距的表達形式如表1所示.

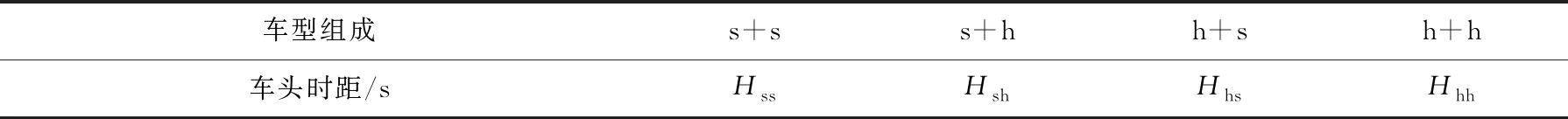
表1 車型組成與車頭時距的表達

蘇岳龍等[5]對某交叉口飽和車流情況下各種車型組成的平均車頭時距進行了調查和統計，結果如下：Hss為2.61 s，Hsh為3.57 s，Hhs為3.36 s，Hhh為4.43 s.可以看出,車型組成對車頭時距的影響顯著.

非飽和跟馳階段車流的車頭時距是由車輛到達率決定的.

1.3 基于LSTM神經網絡的短周期車頭時距預測

學者在用神經網絡預測車頭時距時，一般選用較為簡單的BP網絡[6]，但是BP網絡易陷入局部最小值，記憶能力較弱，且不考慮時間的先后順序.而在信號交叉口中，從1個信號周期內車頭時距的變化來看，車頭時距是具有時間外推性的規律的[7]，這就有必要考慮時間的先后順序這個因素.對此，本文選用處理時間序列數據的LSTM神經網絡模型，可展示動態時序行為，能更好地適應車頭時距的變化.

LSTM神經網絡由遺忘門、輸入門和輸出門組成，通過3個門的結構可以調控任意時刻的狀態和輸出.t時刻LSTM單元狀態的計算公式如下[8-9]:

ft=σ(wf[ht-1,xt]+bf).

(2)

rt=σ(wr[ht-1,xt]+br);

(3)

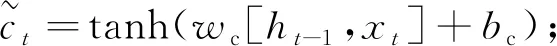
(4)

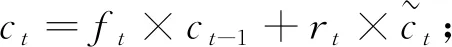
(5)

vt=σ(wv[ht-1,xt]+bv);

(6)

ht=vt×tanhct.

(7)

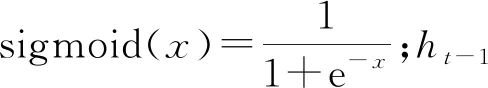
至此，LSTM模型就把當前時刻的信息狀態與過去時刻的信息狀態建立了聯系，通過3個門結構，不僅使得模型能夠對過去時刻的主要信息進行保存，也可以對預測過程中無關緊要的信息進行遺忘.

2 改進感應信號控制的綠燈時間計算

根據車流通過交叉口時的3個階段，可分別計算它們的綠燈時間.

2.1 首車通行階段的綠燈時間G1ij

G1ij與車型有關，通過統計分析小(大)型車的歷史通行時間數據，可得到小(大)型車的首車通行階段的綠燈時間，即

(8)

式(8)中：tos為首車是小型車時的通行綠燈時間(單位：s，下同)；toh為首車是大型車時的通行綠燈時間.

2.2 飽和跟馳階段的綠燈時間G2ij

對于第1部分車輛，由于車型對飽和車頭時距有顯著的影響，所以需要利用感應信號的檢測器檢測各車型組成情況下的車頭時距和車輛數，如表2所示.飽和跟馳階段第1部分的車輛數為qij1，各對應車型組成的車輛數分別為Nss1,Nsh1,Nhs1,Nhh1(單位：veh，下同).

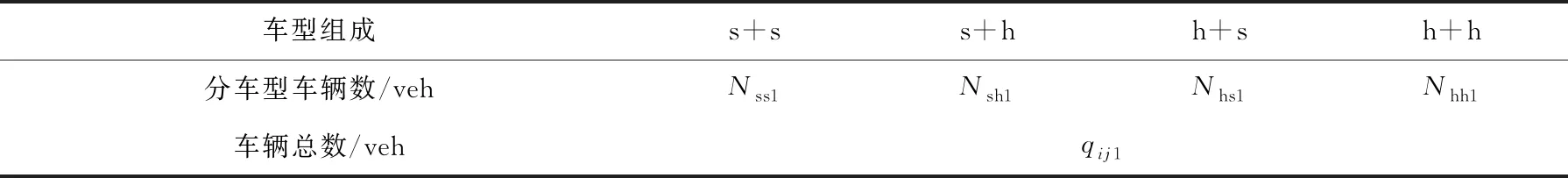
表2 飽和跟馳階段第1部分車輛統計

該部分車輛通行需要的綠燈時間為

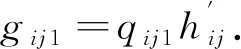
(9)

對于第2部分車輛，它們會在紅燈時就在排隊的車輛之后達到，并形成飽和車流，車隊長度受排隊車流的消散時間和車輛到達率Ki的影響.該部分車輛也應根據車型的組成情況進行統計，不同車型組成的車輛數分別為Nss2,Nsh2,Nhs2,Nhh2，如表3所示.

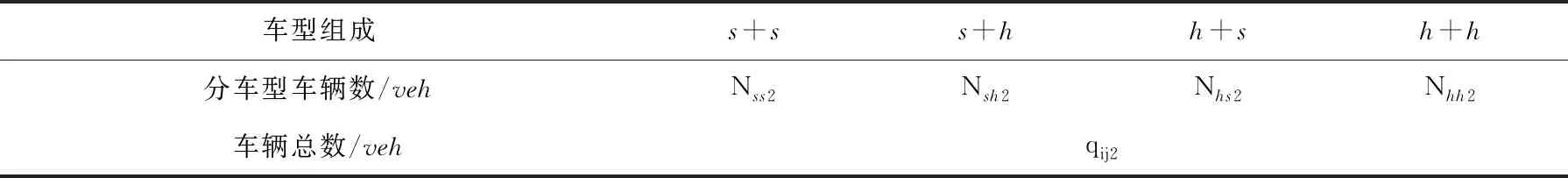
表3 飽和跟馳階段第2部分車輛統計

因此，第2部分的車輛數為

qij2=(G1ij+gij1)Ki.

(10)

其通行所需要的綠燈時間為

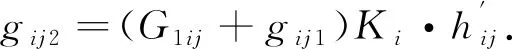
(11)

式(10)～(11)中：Ki為i相位對應車道的車輛到達率(單位：veh/s).

該階段通過的車輛總數為

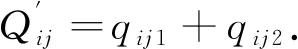
(12)

式(12)中，qij1和qij2的計算公式如下:

qij1=Nss1+Nsh1+Nhs1+Nhh1;

(13)

qij2=Nss2+Nsh2+Nhs2+Nhh2.

(14)

則飽和跟馳階段的綠燈時間G2ij為

G2ij=gij1+gij2.

(15)

式(15)中：

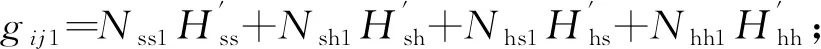
(16)

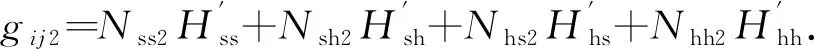
(17)

2.3 非飽和跟馳階段的綠燈時間G3ij

由于本文采用了基于車頭時距的可變單位綠燈延長時間的方式，所以該階段的綠燈時間不再為單位綠燈延長時間乘以該階段到達的車輛數，而是隨車頭時距變化的變值.

每輛車給予的綠燈延長時間gi應小于最大允許的單位綠燈延長時間gimax，其計算公式為

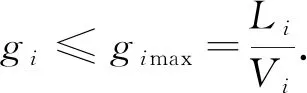
(18)

式(18)中：Li為i相位關鍵進口道檢測器安裝位置與停車線之間的距離(單位：m)；Vi為該路段內車輛的平均車速(單位：m/s).

那么該階段的車輛數也可表示為

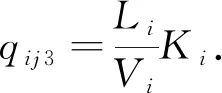
(19)

顯然，當飽和跟馳階段之后的gimax時間內沒有車輛到達時，qij3和G3ij均為0；當有連續n輛車的車頭時距小于gimax，且第n+1輛車的車頭時距大于gimax時，結束本相位綠燈，運行下一相位；當綠燈延長時間達到極限綠燈延長時間Gmax時也應切換相位.非飽和跟馳階段車輛的行駛狀態如圖3所示.

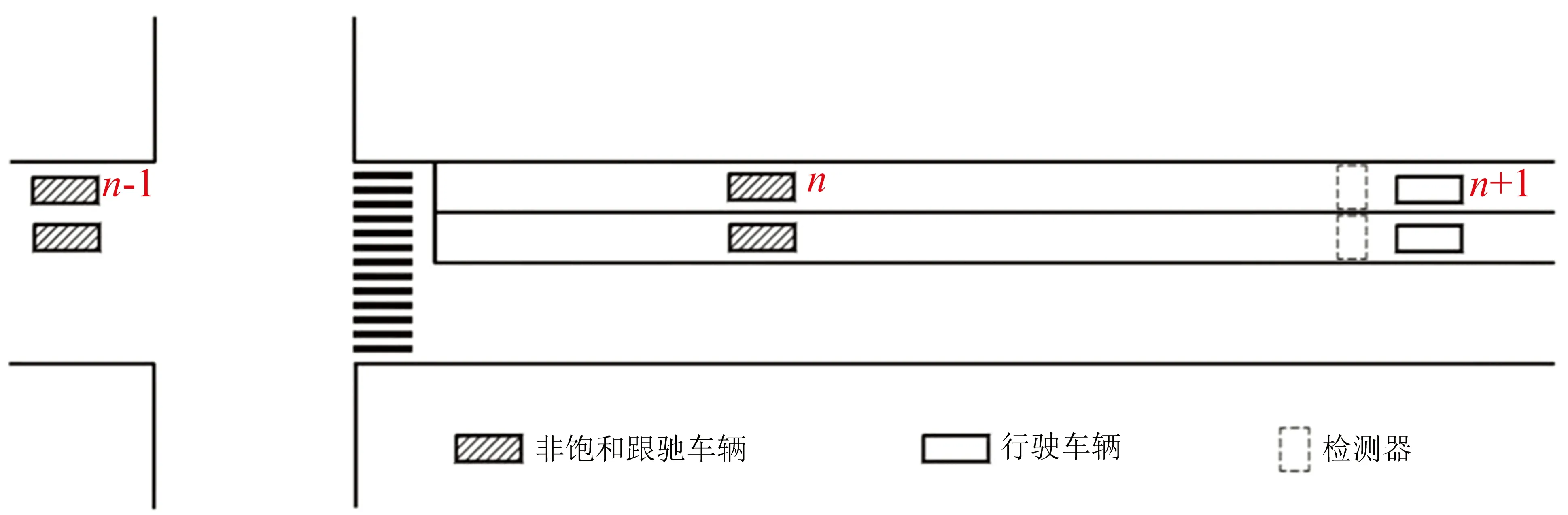
圖3 非飽和跟馳階段車輛的行駛狀態

與第2階段一樣，該階段車輛也需按車型的組成情況進行統計，不同車型組成的車輛數分別為Nss3,Nsh3,Nhs3,Nhh3.

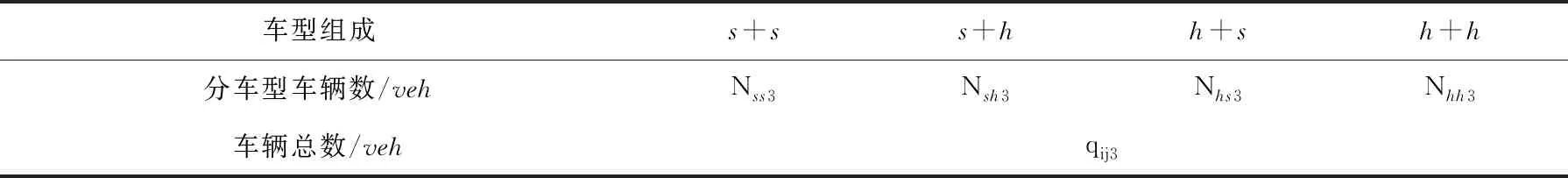
表4 非飽和跟馳階段車輛統計

那么非飽和跟馳階段的綠燈時間為

(20)

2.4 總綠燈時間

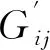
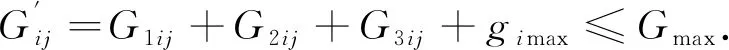
(21)

此外，初始綠燈時間Tic為首車通行階段綠燈時間和飽和跟馳階段第1部分車輛的通行時間，即

Tic=G1ij+gij1.

(22)

3 案例分析

3.1 案例背景

某十字交叉口為2條雙向6車道的城市干道，4個進口道均有3個車道(1個左轉車道、2個直行車道)，并渠化出了右轉匝道.本文以南進口道為例進行模擬仿真，其左轉、直行流量分別為180 veh/h和360 veh/h.

信號相位順序為：南北直行→南北左轉→東西直行→東西左轉.

感應信號相關參數如下：Li=50 m，Gmax=50 s，Vi=35 km/h，gimax=50/(35/360×100)=5.14 s.

車型組成和車頭時距：首車通行和飽和跟馳階段的車型組成為“h+h+s+s+h+s”，非飽和跟馳階段的車型組成為“s+s+s+s+h+s+h”，車頭時距分別為：3.14，3.32，3.25，5.32，4.01，4.04，5.62 s，….

3.2 改進感應信號控制模擬

輸入連續5個周期的交通流流量、速度、車頭時距等參數，基于Python的Keras平臺分別對LSTM神經網絡和BP神經網絡模型進行訓練，進而預測出本周期各車型車輛通過停車線的車頭時距.

LSTM神經網絡的訓練過程如下：本文選取的訓練集和驗證集的比例為3∶1.考慮車輛車型與車頭時距2個變量，其中車輛類型為分類變量，大型車輛為0，小型車輛為1.通過調參，選定以下最佳實驗參數：時間窗步長為5(可根據實際情況改變)，網絡隱藏層為1，輸入神經元個數為2，隱藏層的神經元個數為 64，訓練次數epochs為1 000.運行之后其數據集的平均絕對百分比誤差(MAPE)為0.17，均方根誤差(RMSE)為0.16，訓練和預測的全部耗時為6.70 s，預測耗時為0.08 s.一般信號交叉口的實際周期大于60 s，因此，該方法在實際應用中有足夠的時間預測下一周期的交通流參數.

為驗證LSTM模型的實際效果，本文與BP神經網絡進行了對比.其實驗參數為：網絡隱藏層為11，學習率為0.4，訓練次數epochs為500，預測耗時為1.18 s.運行之后其數據集的MAPE和RMSE值分別為0.22和0.26.

圖4為LSTM和BP神經網絡模型的預測圖，表5為2種模型的衡量指標對比.由此可以看出：BP神經網絡模型的性能較差，易陷入局部最小值；而本文提出的LSTM神經網絡模型充分考慮時間的先后順序及車輛類型，其預測值與真實值的趨勢基本一致.

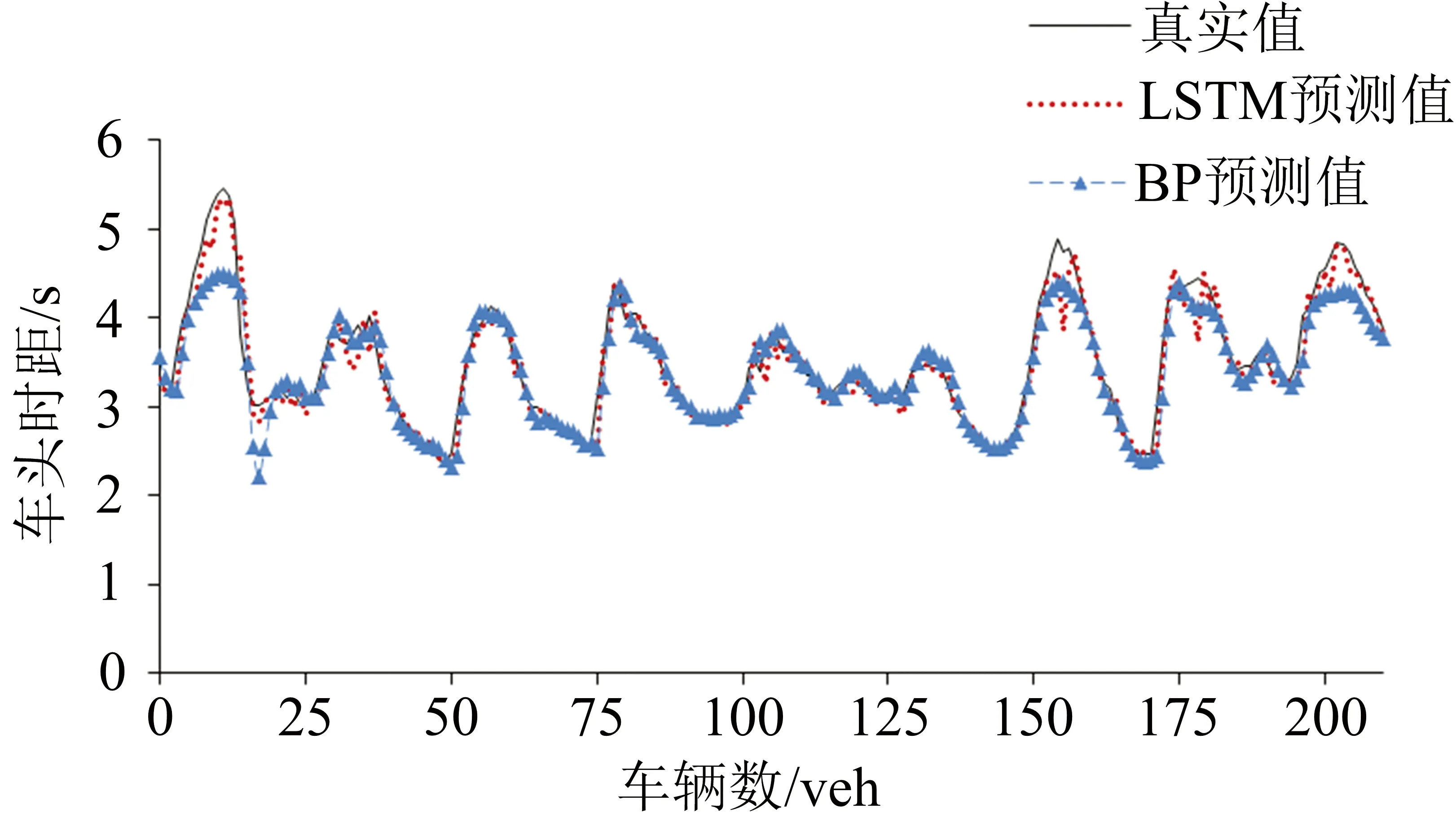
圖4 LSTM和BP神經網絡預測圖

表5 不同模型的對比試驗

輸出結果：預測得到的首車和飽和跟馳階段第1部分車輛的車型組成為“h+h+s+s+h+s”，首車為大型車，即G1ij為4.25 s.

飽和跟馳階段第1部分有5輛車，由式(16)計算可得gij1=4.26+3.32+2.51+3.14+3.86=17.09 s.

那么初始綠燈時間Tic=4.25+17.09=21.34 s.

在Tic時間內共有6輛車以飽和車頭時距跟馳而來，其車型組成為“s+s+s+s+h+s”，由式(17)計算可得gij2=4×2.51+3.14+3.86=17.04 s.

因此，前面2個階段共通行12輛車，耗時為：G1ij+G2ij=G1ij+gij1+gij2=4.25+17.09+17.04=38.38 s.

預測第13輛車與前車的車頭時距為5.62 s，大于gimax的5.14 s，所以在此之后切換相位.

3.3 傳統感應信號控制模擬

1)初始綠燈時間

該時間為關鍵進口道最大排隊的消散時間，即[10]

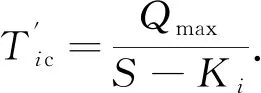
(23)

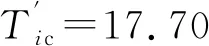
2)單位綠燈延長時間

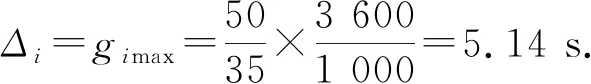
3)極限綠燈延長時間

與改進感應信號控制一樣，為50 s.

4)總綠燈時間

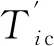
3.4 2種感應信號控制的對比

將改進的感應信號控制和傳統的感應信號控制結果進行對比，結果如表6所示.

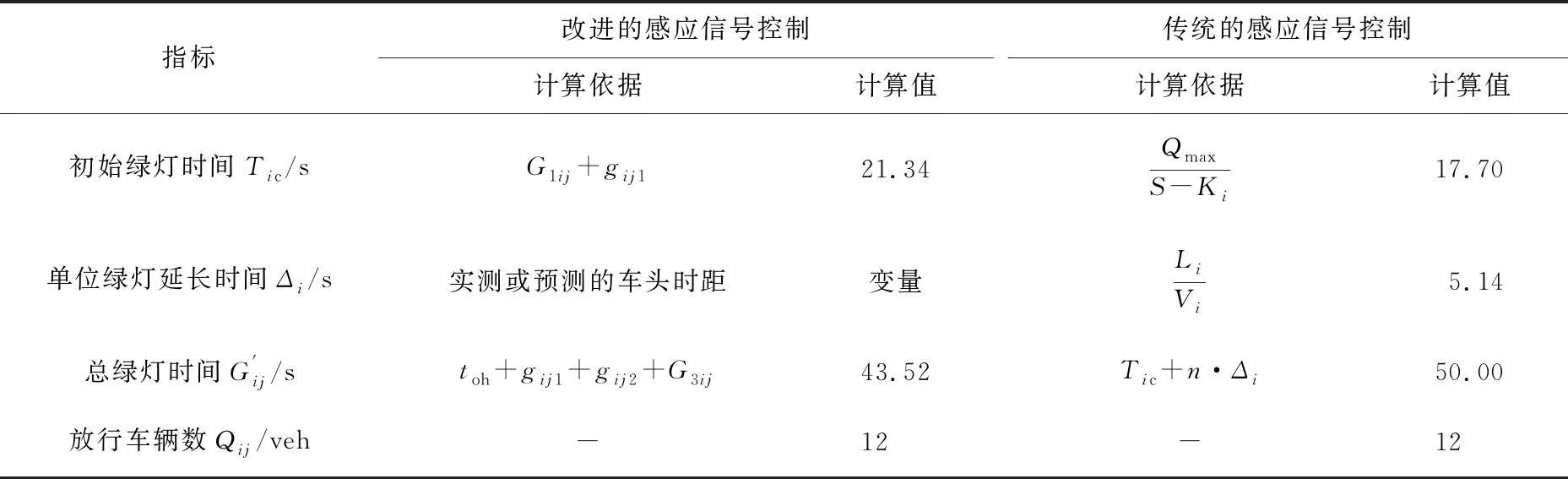
表6 改進和傳統感應信號控制關鍵參數計算對比

從數據對比中可以看出：在改進的感應信號控制和傳統的感應信號控制均放行12輛車的情況下，二者的實際綠燈時間分別為43.52 s和50 s，相差6.48 s，差異率為14.89%.該6.48s時間存在2種可能：

1)在此時間內有車輛到達且通過交叉口，則車輛通行時間外的時間為延誤；

2)在此時間內無車輛到達或無車輛通過交叉口，則6.48 s均為交叉口延誤.因此,改進的感應信號控制比傳統的感應信號控制減少的延誤為0～6.48 s.

4 結 論

本文以感應信號控制交叉口為研究對象，采用LSTM神經網絡對車頭時距進行預測，并依此設置綠燈延長時間.結果表明：

1)根據LSTM神經網絡的車頭時距預測模型得到的預測值與真實值的趨勢基本一致，MAPE和RMSE的值分別為0.17和0.16，擬合情況良好.

2)依據LSTM模型預測得到各車型組成的車頭時距，動態設定到達車輛的綠燈延長時間，能有效提升綠燈的使用效率，控制效果更佳，通行延誤更少.在案例中，相比較于傳統感應信號控制的交叉口，采用該模型的改進效果顯著，通行效率可提高14.89%.

3)該方法的訓練和預測時間較短，能應用于實際信號控制中.