BP-Garson算法的高橋隧比路段交通事故預測研究

曹雪娟，黃銘軒，吳博文，楊曉宇

(重慶交通大學 a.材料科學與工程學院; b.土木工程學院， 重慶 400074)

因自然環境復雜性，山區高速公路的修建通常會應用到大量隧道、橋梁等構造物。其中，橋隧比例較高的道路路段可被稱為高橋隧比路段，本文將橋隧比定義為：橋隧比=(橋梁里程+隧道里程)/路段總里程。隧道、橋梁等構造物的修建雖然有助于高速公路順利通向各個地區，但橋隧相連、坡陡彎急和持續長大縱坡等路段的交通事故率仍然高居不下[1]。山區高速運營安全形勢嚴峻，交通事故的發生不僅會給駕乘人員帶來諸多不便，嚴重時還會造成人身安全問題。此外，各山區高速公路常常作為物資運送的大動脈，交通一旦中斷，群眾的生產生活就會受到影響。為降低山區高速公路交通事故發生率，利用已有交通事故數據對交通事故各因素的內在關系進行分析具有重要意義。路面路表性能是影響交通事故的重要道路條件，盡管學者們已對此做出相關研究，但是路表數據獲取困難、處理復雜，使得研究進展受限[2-4]。

研究表明，采用人工神經網絡算法對路面路表性能的數據點進行非線性映射逼近處理，可以實現性能參數的有效整合。Garson算法能夠調用權重矩陣對構建的預測模型進行重要性分析，得到輸入參數與輸出參數的權重關系。因此，本文采用BP神經網絡算法和Garson算法，依托路面養護數據建立高橋隧比路段的交通事故預測模型。采用監督分類法分析高橋隧比路段的交通事故數據，研究路面路表性能參數對高橋隧比路段交通事故的影響，并為山區高速公路交通事故預防及路面養護建設提供建議。

1 研究方法和理論基礎

1.1 基于R語言的BP-Garson組合算法

R語言平臺因其結果可視化，依托其實現的神經網絡已被應用于各種研究領域[5-7]。誤差逆傳播算法(error back propagations，BP)是神經網絡中的一種常用類型，也稱為BP神經網絡，該算法理論清晰且適合非算法研究工程設計人員使用[8-11]。神經網絡結構如圖1示。Garson算法將網絡結構中的每個輸入信號間的連接權值作為“橋梁”，通過權值矩陣計算出每個輸入參數對輸出參數的相對貢獻值。

圖1 BP神經網絡結構示意圖

1.2 監督分類算法

常見的文本分類算法有無參數型的樸素貝葉斯[12]、決策樹法[13]、支持向量機[14]等。在實際應用中，監督分類算法能較好地解決許多量大復雜的分類工作，基于文本數據利用監督分類算法進行分類器設計的研究成果豐碩。在監督分類中，首先需要一定數量的原始訓練樣本，通過參數統計得出每一類別的統計特征量，并用某種分類算法對其進行訓練得出分類模型，最后利用該模型對整個原始數據進行分類。

2 數據預處理和評價方法

2.1 研究參數的預處理

2.1.1路段劃分和數據采集

高速公路路段劃分有幾種常用方法[15]，其中定長法以高速公路里程樁為劃分路段的依據，確定一定長度的路段，將全線劃分為連續的等長路段單元。本文研究段的地理位置如圖2所示，起訖點樁號為K1672+332～K1995+666，路段全長約324 km，橋隧道總長為181 km，路段總體橋隧比約56%。以每公里作為一個路段進行劃分，對采集數據進行處理，分別得到路面行駛質量指數(RQI)、路面橫向力系數(SFC)和路面車轍深度指數(RDI)，如表1所示。

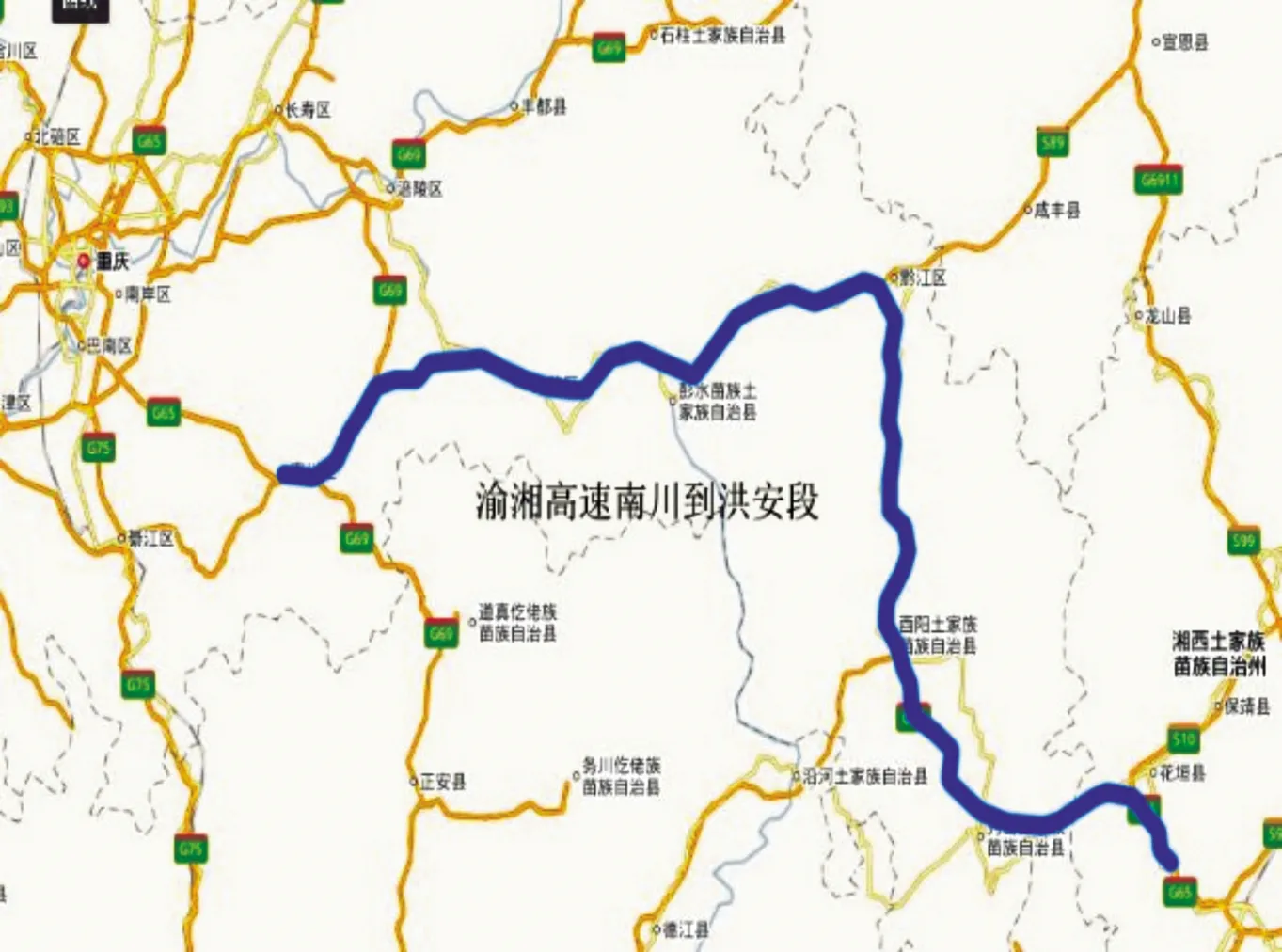
圖2 具體研究段地理位置示意圖

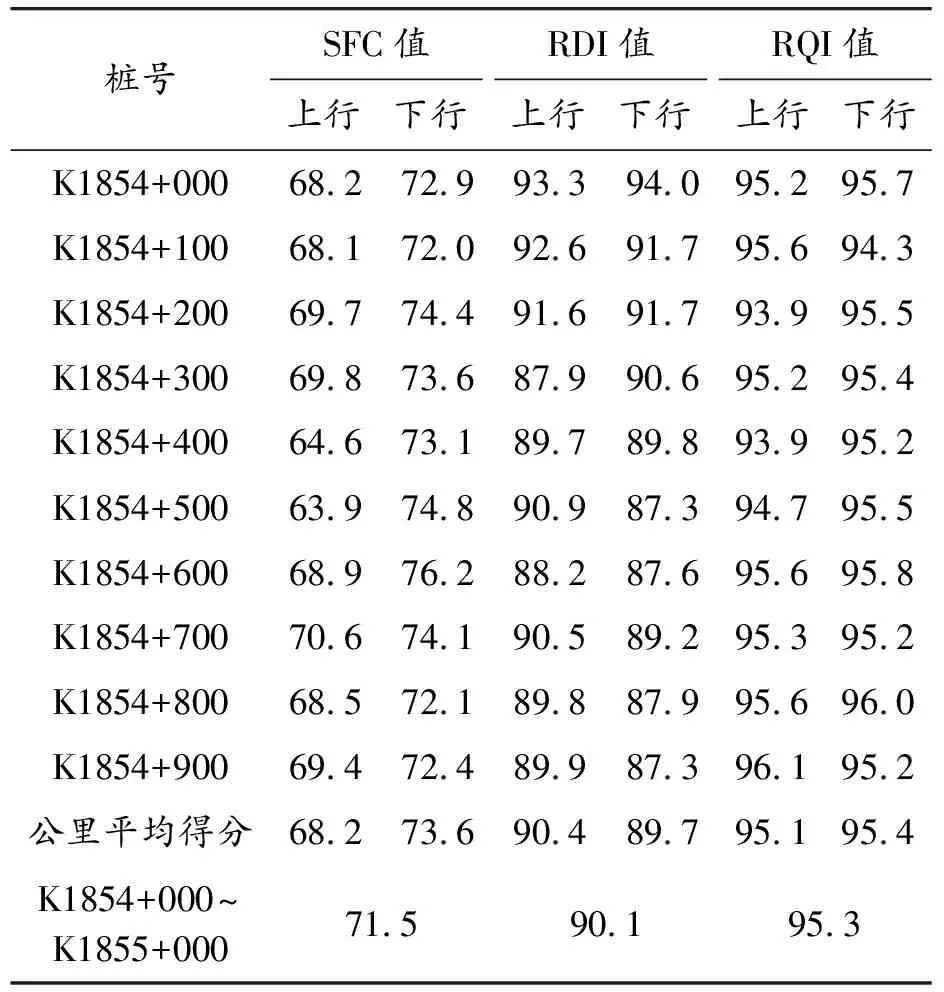
表1 每公里路面路表采集數據的數據預處理(數據節選自2015年)

2.1.2輸入參數的歸一化處理

為了優化神經網絡的訓練建模，需要對原始數據預處理后得到的輸入參數進行歸一化處理，這樣既能使原始數據無量綱化，又能減少參數量級不同對結果造成的影響，計算公式如下。

(1)

2.1.3輸出參數的二值分類

分類監督算法的核心在于對文本詞義進行正確的抽象處理，使算法輸出的結果有效。本研究采用邏輯回歸統計特征量的二值分類思想，抽取事故路段中頻繁出現的橋隧段作為研究對象，將橋隧段發生的交通事故作為輸出記為1，非橋隧段的交通事故輸出記為0。

2.2 基于混淆矩陣的預測模型評價

2.2.1基于混淆矩陣的量化模型評價

為了量化評價模型的擬合效果，二值分類系統中常用評價指標有準確度、精確度和召回率。基于混淆矩陣對二值分類(ture or false)模型進行評估，準確度(Accuracy，ACC)越接近1則表示模型越優。混淆矩陣及模型的評價公式如表2和式(2)—(4)所示。精確度(precision)用于評價預測結果，用來表示預測為真的樣本中正樣本的數量。召回率(recall)用于評價模型預測時原始樣品的選擇情況，表示樣本中的正例被預測正確的數量。

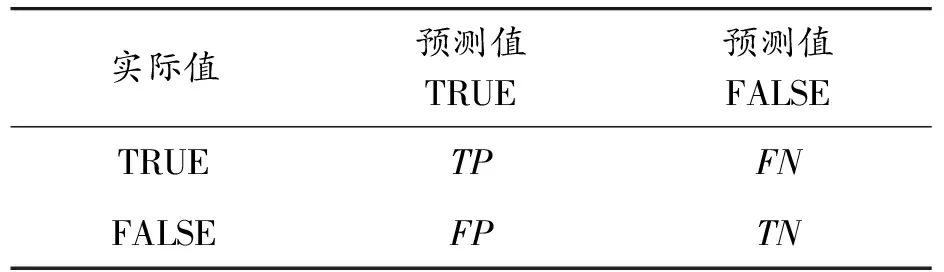
表2 二值分類的混淆矩陣

(2)

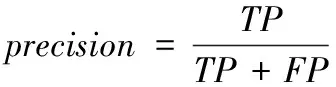
(3)

(4)

2.2.2受試者工作特征曲線

受試者工作特征曲線(receiver operating characteristic,ROC)是利用圖形可視化方法來展現二值分類系統預測能力的一種評價手段。通過式(5)繪制真陽性比例(ture positive rate，TPR)-假陽性比例(false positive rate，FPR)圖，利用傳統模型分析的靈敏度(Y軸)和特異性(X軸)綜合反映預測模型的準確性。本文根據曲線位置將該圖劃分為兩部分，曲線下方的面積被稱為AUC(area under curve)，AUC值越高，曲線越接近左上角(即X越小，Y越大)，說明預測準確率越高，如圖3所示。

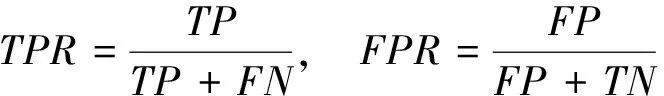
(5)

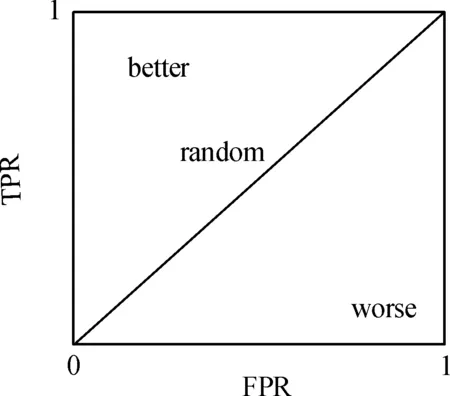
圖3 ROC曲線評價示意圖

2.2.3高橋隧比路段交通事故的重要性分析

高橋隧比路段交通事故的重要性分析是一種權重分析方法，用于描述某一因素或指標對研究目標的整體影響，更強調因素或指標間的相對重要性。本文所用的BP-Garson組合算法，是將每個隱含層神經元的“隱含層-輸出層”連接權值分配到與其相連輸入信號的連接權值上，依據式(6)，確定了每個輸入值對輸出值的貢獻量。

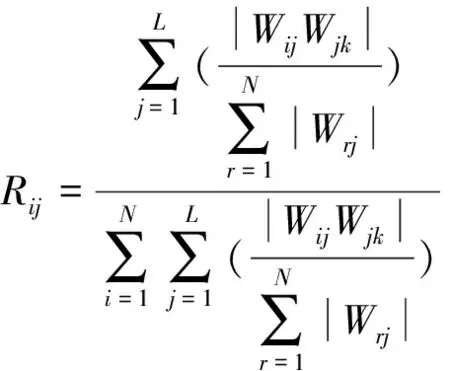
(6)

式中：Rij為輸入信號相對重要性；Wij、Wjk分別為輸入層-隱含層、隱含層-輸出層間連接權值；i=1,2,…,N;k=1,2,…,M(N、M分別為輸入信號、輸出信號個數)。

3 模型建立

3.1 基于R語言的數據處理

建立的預測模型采用編碼加函數調用的形式完成，所調用的函數資源見表3。

表3 神經網絡調用的函數資源包

首先調用matrixPlot函數分析交通事故原始數據集，結果如圖4示，灰度由淺到深表示數值從小到大，紅色部分表示缺失數據。然后進行數據清洗，根據相關處理缺失數據理論[16]，剔除掉不完整的129項數據，占數據集總量的4.8%。最后將預處理的數據集整理保存，其參數內容如表4所示。

圖4 R語言預處理的交通事故數據矩陣圖

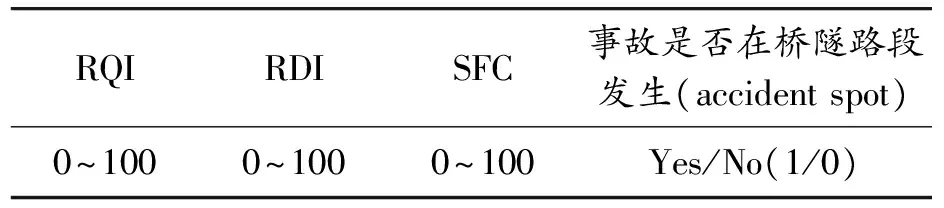
表4 神經網絡建模的輸入輸出參數

3.2 預測模型的建立

3.2.1建立模型的歸一化處理

將按路段劃分的20段事故數據中2 707組有效輸出參數及預處理輸入參數進行歸一化處理，結果如表5所示。

3.2.2BP-Garson算法的預測模型建立

“路面性能—橋隧段發生事故”樣本的訓練模型采用輸入層、隱含層和輸出層3層結構。將采集的RQI、SFC和RDI相關數據作為事故路段的路面性能輸入參數，以交通事故發生地點是否位于橋隧段作為輸出參數，構建二值分類的高橋隧比路段交通事故預測模型。調用函數包“Neuralnet”，參考相關文獻[8,17]，依據式(7)判斷隱含層神經元訓練個數范圍在2～12，預測模型的訓練結果以8個隱含層神經元為例，如圖5所示。

(7)

其中：k為隱含層神經元個數；m為輸入端參數個數；n為輸出端參數個數；a=0～10。

表5 節選自2015年事故處理數據

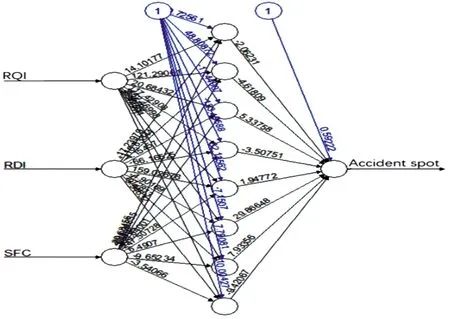
圖5 “路面性能—橋隧段事故發生”的預測模型示意圖(8個隱含層神經元)

設置隨機數種子Seed，訓練預測模型得出的結果如表6示。可以發現，不同個數的隱含層神經元所構建的二值分類預測模型存在差異，這是神經網絡算法本身網絡結構所決定的。針對訓練模型存在的波動性差異，本文利用k=3、5、8這3組預測模型對比分析高橋隧比路段交通事故的發生規律。從2014—2016年的“路面性能—橋隧段發生事故”樣本中隨機抽樣得出70%的數據，通過訓練建立預測模型，把剩余的30%事故數據用于模型擬合效果的評價。

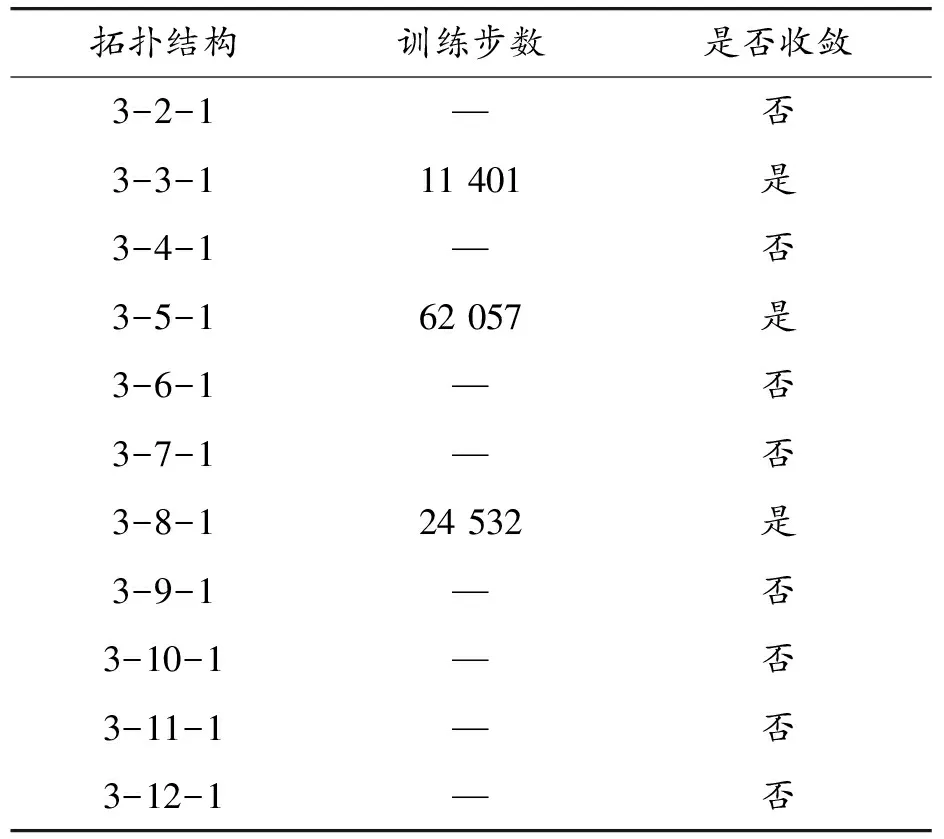
表6 橋隧段發生交通事故預測模型的訓練結果

4 預測模型的評價

4.1 預測模型的受試者工作特征曲線

不同隱含層神經元訓練的ROC曲線均位于random曲線的左上方，這意味著所建立的預測模型具備可靠性[18]。如圖6所示，隱含層神經元個數為8的ROC曲線位于最左上方，說明模型的預測精度較其他曲線最大。此外，預測模型的擬合效果隨隱含層神經元個數的增多而提高，表明網絡結構復雜化有利于提高模型精度。

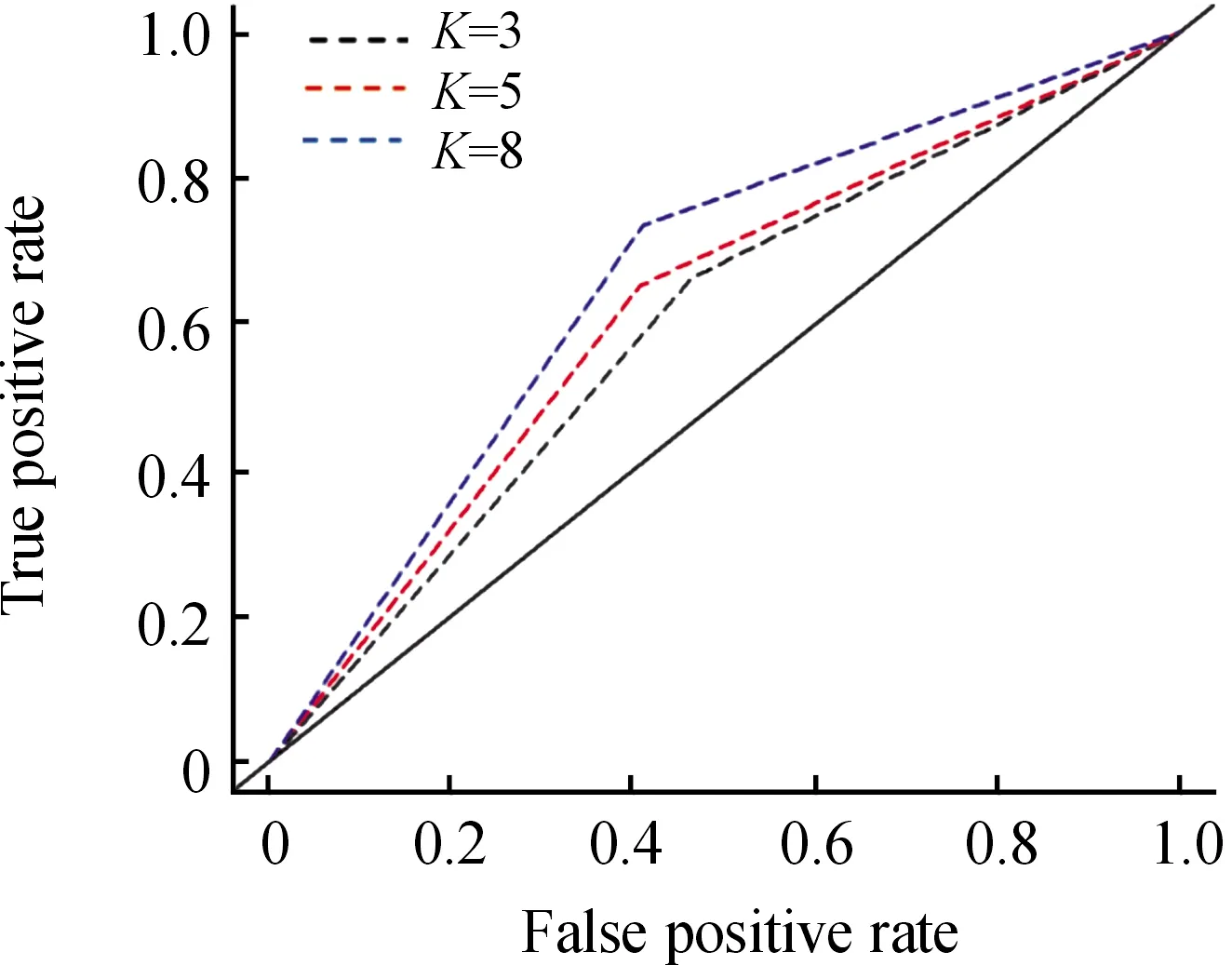
圖6 “路面性能—橋隧段事故發生”的ROC曲線

4.2 模型的準確度對比

依據混淆矩陣分析高橋隧比路段2014—2016年的交通事故發生率，結果如表7所示。預測模型的訓練結果ACC為0.6～0.7，代表該模型擬合效果好[16]。為了進一步量化預測模型擬合效果，采用精確度及樣本召回率對其分析。隱含層神經元個數為8時的預測精度最高，可達0.612；神經元個數為5時的樣本召回率最高，為0.593。神經元個數為8時的預測模型能防止結果過擬合，并兼顧結果的準確度，能更好地滿足預測要求。從實際預測值來看，該模型在30%測試樣本下的預測事故率也逼近了所對照的樣本事故率。

表7 BP預測模型的擬合效果

4.3 重要性分析

傳統BP神經網絡預測模型僅能依據黑箱算法給出預測的輸出值，而BP-Garson組合模型能對訓練模型各因素的組成貢獻進行分析。本研究調用R語言的“NeuralNetTools”包的Garson算法編寫分析代碼，將預測模型各參數的重要性對比結果進行可視化分析。為保證預測結果具有典型性，分別對不同隱含層神經元建立的預測模型進行模型參數的重要性分析，結果如圖7所示，k值代表不同隱含層神經元的個數。3種性能參數的重要性排序結果表明，SFC是影響高橋隧比路段交通事故發生率的主要影響因素，RQI和RDI為次要因素。

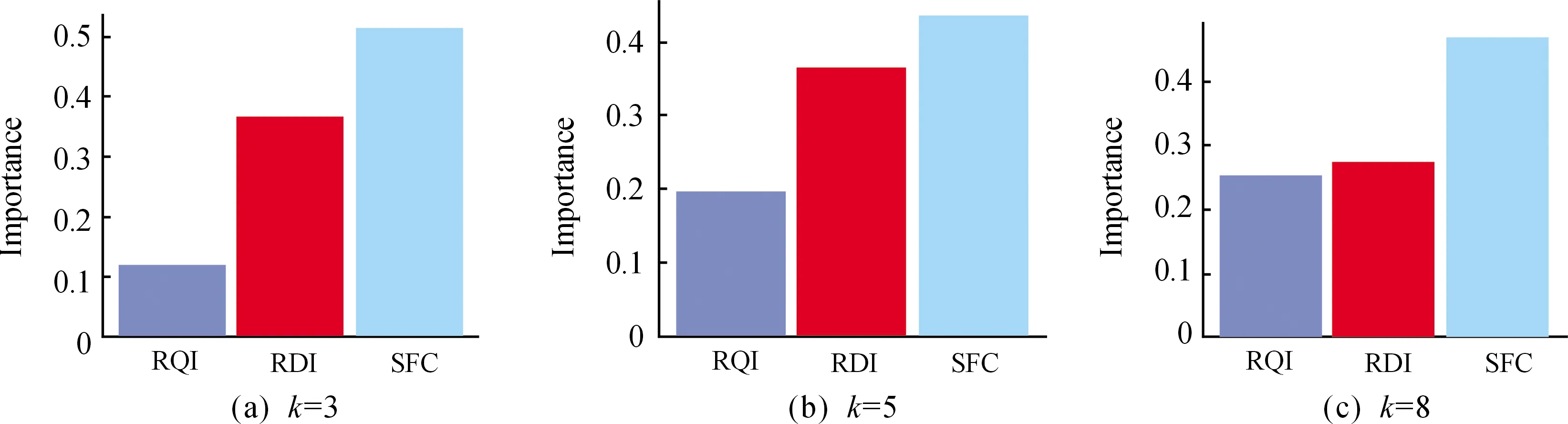
圖7 路表性能各指標占預測模型的重要性分析結果

5 結論

1) 二值分類預測模型的擬合效果較好。對3年間近3 000組的交通事故數據進行訓練建模，所建立的BP-Garson預測模型ACC最高可達0.674，具有較好的擬合效果，分析ROC曲線發現，當隱含層神經元個數為3、5和8時，預測模型的AUC面積均大于random曲線。

2) 模型的預測結果精確度高。預測模型的精確度隨隱含層神經元的個數增加而提高，當神經元個數為8時，預測精確度高達61.2%，樣本召回率為59.0%。研究發現在SFC、RQI、RDI這3種路面性能參數中，SFC值是高橋隧比路段交通事故發生的主要影響因素。

3) 基于二值分類系統預測交通事故影響因素的方法具備可行性。依據路面路表性能可以較好地判斷出該高橋隧比路段的事故發生率，在樣本事故率為41.6%時，8個神經元模型預測的事故發生率達40.0%。

4) BP-Garson預測模型可用于山區高速交通事故率的預測研究。預測模型的擬合效果和重要性分析的結果均表明，僅依靠收集路面路表性能就可在一定誤差范圍內預測同一路段的事故發生率。