基于BP神經(jīng)網(wǎng)絡(luò)與遺傳算法的攔污柵結(jié)構(gòu)優(yōu)化設(shè)計
王亞輝 張慧鵬 尚力陽等

關(guān)鍵詞:攔污柵;均勻試驗設(shè)計;BP神經(jīng)網(wǎng)絡(luò);遺傳算法;優(yōu)化設(shè)計;南水北調(diào)工程
中圖分類號:TV732.2 文獻標志碼:A doi:10.3969/j.issn.1000-1379.2022.03.022
引用格式:王亞輝,張慧鵬,尚力陽,等.基于BP神經(jīng)網(wǎng)絡(luò)與遺傳算法的攔污柵結(jié)構(gòu)優(yōu)化設(shè)計[J].人民黃河,2022,44(3):112-117.
南水北調(diào)工程中許多帶有攔污柵結(jié)構(gòu)的河道攔藻設(shè)備投入使用。攔污柵工作時并不穩(wěn)定,水通過攔污柵時,柵條尾部脫流產(chǎn)生的卡門渦街引起激振力,該激振力的頻率一般與流速成正比,柵條的尺寸、形狀和連接方式很大程度上決定了柵條的自振頻率。當攔污柵表面作用力的頻率和自振頻率相近時,會產(chǎn)生渦柵共振,極易造成攔污柵破壞。一般理論上認為,避免攔污柵共振現(xiàn)象的關(guān)鍵是讓柵葉的自振頻率在水流激振頻率的15%范圍之外,但實際運行中解決該問題比較困難。
隨著計算機技術(shù)的發(fā)展,有限元軟件的應(yīng)用日臻成熟,模型仿真結(jié)果的可靠性大幅提升,傳統(tǒng)的模型試驗逐漸被取代。鑒于以上情況,本文提出了一種減少以攔污柵為主要結(jié)構(gòu)的渦柵共振現(xiàn)象的同時又減小攔污柵自重的方法,為尋求柵葉各結(jié)構(gòu)參數(shù)的最優(yōu)組合,利用均勻設(shè)計試驗法在攔污柵各參數(shù)取值范圍內(nèi)選取若干樣本點,并基于solidworks19.0強大的三維建模能力建立攔污柵參數(shù)化3D虛擬模型,將模型導入ANSYS中,通過Fluent軟件計算各樣本點柵葉模型的卡門渦街旋渦的脫落頻率,再通過模態(tài)分析計算柵葉在液固耦合狀態(tài)下的各階自振頻率,然后在MATLAB中運用BP神經(jīng)網(wǎng)絡(luò)結(jié)合遺傳算法對各參數(shù)下的試驗結(jié)果進行分析比較,最后求解出柵葉的最優(yōu)參數(shù)組合。
1結(jié)構(gòu)模型
南水北調(diào)工程中采用黃河水利委員會黃河機械廠研發(fā)的全自動攔藻設(shè)備已通過試運轉(zhuǎn)試驗,此設(shè)備安裝于渠道檢修閘門槽,主材為不銹鋼,主要包括驅(qū)動機構(gòu)、鏈網(wǎng)機構(gòu)、傳動機構(gòu)、沖洗噴淋裝置、污水集排裝置等。機器通過PLC控制,可根據(jù)藻類發(fā)生情況的輕重程度自動完成攔撈、沖洗、收集、排放作業(yè);當水藻污染較重時,傳動機構(gòu)中的鏈條帶動旋網(wǎng)及齒耙繞著攔污柵旋轉(zhuǎn),帶走水中的水藻等污染物;等污染物跟著鏈條傳動到河道工作臺上方時,沖洗噴淋裝置會將旋網(wǎng)上附著的水藻等污染物沖到污水集排裝置中,從而實現(xiàn)不間斷除藻功能。此設(shè)備的總工作流程得以實現(xiàn)的根基是有攔污柵作為支撐,攔污柵主框架要承受較大的自重,因此其尺寸較大,一般不會發(fā)生因水流的沖擊振動而造成破壞的現(xiàn)象。柵葉一般長度較長,寬度較窄,厚度較薄,因此強度較弱,在水流的沖擊下易發(fā)生渦柵共振而造成結(jié)構(gòu)破壞[1],將柵葉做得又厚又寬,不太符合設(shè)計的規(guī)范性,而按照傳統(tǒng)經(jīng)驗設(shè)計很難估算出最佳的柵葉尺寸。
本文使用solidworks19.0對南水北調(diào)全自動攔藻除污設(shè)備的攔污柵進行參數(shù)化三維建模,如圖1所示,并取其中的一段攔污柵結(jié)構(gòu)進行有限元分析。攔污柵材料為不銹鋼,垂直高度5.5m,與水面之間的傾斜角為60°,每組傳動機構(gòu)水平間距1m,在這1m的間距中設(shè)置多條柵葉,將柵葉的水流沖擊面做成圓弧形,此時水流沖擊柵葉時無大的轉(zhuǎn)折角,水流平緩流過柵葉,水頭損失最小[2]。柵葉的寬度方向垂直于攔污柵主平面。柵葉的長度為L1,柵葉厚度為L2,柵葉寬度為L3,兩相鄰柵葉距離為L4。
2均勻設(shè)計試驗
因優(yōu)化的參數(shù)只有L1、L2、L3、L4,故從盡量多做試驗提高試驗準確性的角度考慮,在咨詢相關(guān)技術(shù)人員后,確定這4個變量的取值范圍,見表1。
根據(jù)均勻設(shè)計試驗U13(134)表的各因素對應(yīng)于各水平的排列情況,編寫實際應(yīng)用的均勻設(shè)計試驗安排,見表2。
3控制方程及數(shù)值模擬
3.1控制方程
柵葉自振頻率f的計算可根據(jù)參考文獻[3]的建議采用levin公式:
式中:E為柵條材料的彈性模量;I為柵條橫截面的慣性矩;g為重力加速度;m為柵條的質(zhì)量;L為柵條在支撐梁間的長度;β為與支撐方式有關(guān)的系數(shù),對于兩端固定支撐β≈22.4,對于兩端簡單支撐β≈9.87,對于柵條兩端焊接情況取β≈16,本研究取β=16[4]。
考慮液固耦合因素對水下柵葉自振頻率的影響[5],水體附加質(zhì)量法可以很好地用來計算液固耦合下結(jié)構(gòu)自振頻率fn,因此采用修正的levin公式:
式中:mw為與單位長度相應(yīng)的水體附加質(zhì)量;A為柵條截面面積;B為柵條之間的有效間距;D為柵條的厚度;γw為水的密度。
清華大學水利工程系王光綸團隊[4]計算得出固液耦合狀態(tài)下自振頻率降低了27%左右,但其后期的模型試驗結(jié)果與公式法結(jié)果有差異,其給出的觀點是攔污柵的整體結(jié)構(gòu)對單個柵葉有影響,從而造成柵葉不能成為獨立結(jié)構(gòu),影響了試驗結(jié)果的準確性,造成試驗結(jié)果與公式計算結(jié)果的差異,但公式法依然有一定的實用性。后續(xù)大量試驗也證明了這一觀點,比如:張炎炎[5]的試驗結(jié)果表明,固液耦合因素影響下結(jié)構(gòu)的自振頻率比結(jié)構(gòu)在空氣中的自振頻率降低了28%左右;申永康等[6]的試驗結(jié)果表明,固液耦合因素影響下結(jié)構(gòu)的自振頻率比在空氣中降低了27%左右。上述研究表明,水體附加質(zhì)量法計算固液耦合作用下柵葉的固有頻率確實有很大的可行性。
通過有限元分析軟件ANSYS中的模態(tài)分析模塊計算結(jié)構(gòu)在空氣中的自振頻率,再乘以比例系數(shù)得到結(jié)構(gòu)在水下的自振頻率fn[7]。測量柵葉因水流沖擊而造成的激振頻率,通過Fluent軟件分析柵葉的卡門渦街現(xiàn)象來完成。卡門渦街現(xiàn)象十分常見,例如水流過橋墩、風吹過高塔等都會形成卡門渦街[8-9],激振頻率正是卡門渦街渦旋尾部的脫落頻率。大量試驗表明,渦街的脫落頻率fv和繞流速度v成正比,與繞流寬度d成反比,即
fv=Srvd (4)
式(4)可用來驗證激振頻率的準確性,其中Sr為斯特勞哈爾數(shù),主要與雷諾數(shù)有關(guān),當雷諾數(shù)為300~3×105時Sr近似于常數(shù)0.21,當雷諾數(shù)為3×105~3×106時渦街變得不規(guī)律,當雷諾數(shù)大于3×106時又出現(xiàn)有規(guī)律的渦街現(xiàn)象,此時Sr變?yōu)?.27,本文取Sr=0.21。
3.2數(shù)值模擬
3.2.1劃分結(jié)構(gòu)網(wǎng)格
先對柵葉結(jié)構(gòu)進行模態(tài)分析,在模態(tài)分析中進行網(wǎng)格劃分,柵條結(jié)構(gòu)由長方體組成,為了提高計算精度和計算效率,采用六面體進行網(wǎng)格劃分,網(wǎng)格的密集程度和計算精度正相關(guān),但網(wǎng)格過密會極大延長計算時間,一般將劃分網(wǎng)格的數(shù)目設(shè)置在合理的范圍之內(nèi)。
試驗表明,網(wǎng)格數(shù)設(shè)定在80萬以上即可達到精度要求,柵葉結(jié)構(gòu)的模態(tài)網(wǎng)格劃分如圖2所示。Fluent卡門渦街仿真效果和網(wǎng)格的密集程度密切相關(guān),把全局網(wǎng)格劃分的最小尺寸設(shè)為0.002m,局部進行加密的最小尺寸設(shè)為0.001m,如圖3所示。
3.2.2設(shè)計試驗
結(jié)構(gòu)參數(shù)值決定試驗數(shù)據(jù)的大小,圖2與圖3中模型的參數(shù)屬于均勻設(shè)計試驗表中的一組,其中柵條三維模型中柵條寬度為5cm、厚度為0.5cm,將劃分好網(wǎng)格的三維模型進行模態(tài)分析,約束除中間柵條表面之外的其他所有面,其中1階、3階、6階振型見圖4~圖6。求解得出各階固振頻率,見表3。
3.2.3固液耦合下柵條固振頻率計算
通過式(1)~式(3)計算水中柵葉與空氣中柵葉固振頻率的比例系數(shù),試驗法所得結(jié)果乘以該系數(shù)得出固液耦合下柵條的固振頻率,見表4。
此方法得來的固液耦合下柵條固振頻率未通過試驗確定準確性,但業(yè)內(nèi)多位專家的研究顯示此法可行,本文用此方法作為試驗數(shù)據(jù)的得出依據(jù),并在此取與激振頻率最相近的那階固振頻率作為試驗數(shù)據(jù)。
柵條的激振頻率通過Fluent中卡門渦街試驗求得。圖3二維Fluent模型中3個矩形孔的尺寸對應(yīng)柵條的截面積尺寸,根據(jù)實際考察,水流進柵流速在1~2m/s之間,設(shè)此速度v為2m/s,水介質(zhì)密度為1000kg/m3,進行流體力學分析,得出卡門渦街仿真結(jié)果,如圖7所示。因速度較小,雷諾數(shù)較小,故其渦旋脫落動畫無法顯示[10-11],可通過有限元分析報告來求試驗結(jié)果,保存每一步結(jié)果,得到壁面上某點的壓力隨時間的變化數(shù)據(jù),將此數(shù)據(jù)導入Excel中繪制折線圖,其前面的一段見圖8,并將此組數(shù)據(jù)進行傅里葉變換,得出頻率。
由圖8可知,大約每隔t=0.012s壓強實現(xiàn)一輪升降。由公式fv=1/t可知,fv=83.33Hz。由式(4)計算得到fv=84Hz,與試驗結(jié)果相近,驗證了試驗的準確性。
通過上述試驗方法,對均勻試驗安排表2中的13組試驗分別求出固振頻率和激振頻率,再求出固振頻率與激振頻率的比值,然后根據(jù)各組試驗數(shù)據(jù)求出柵葉的質(zhì)量,見表5。
4BP神經(jīng)網(wǎng)絡(luò)預測人工神經(jīng)網(wǎng)絡(luò)可以產(chǎn)生一種類似大腦神經(jīng)突觸連接的結(jié)構(gòu),運用此結(jié)構(gòu)可以得出信息處理的數(shù)學模型。
人工神經(jīng)網(wǎng)絡(luò)是一種運算模型,這種模型包含大量相互連接的節(jié)點,每個節(jié)點代表一種特定的輸出函數(shù),簡稱激勵函數(shù),每個節(jié)點的連接稱為權(quán)重,代表人工神經(jīng)網(wǎng)絡(luò)的記憶[12]。人工神經(jīng)網(wǎng)絡(luò)可以很好地逼近任何函數(shù),用來處理多變量非線性優(yōu)化問題。BP神經(jīng)網(wǎng)絡(luò)是人工神經(jīng)網(wǎng)絡(luò)的改進版,是一種誤差逆?zhèn)鞑ド窠?jīng)網(wǎng)絡(luò),可學習和儲藏大量輸入與輸出之間的映射關(guān)系,而不需事先描述這種映射關(guān)系的數(shù)學方程[13]。
柵葉結(jié)構(gòu)優(yōu)化屬于多因素非線性優(yōu)化問題,適合用BP神經(jīng)網(wǎng)絡(luò)進行其輸入、輸出參數(shù)之間映射模擬。由均勻試驗設(shè)計表2和仿真結(jié)果表5可知,此優(yōu)化參數(shù)中含有4因素13水平2輸出,因此選用三層BP神經(jīng)網(wǎng)絡(luò),輸入層含4個神經(jīng)元,隱層含5個神經(jīng)元,輸出層含2個神經(jīng)元,借助MATLAB工具,隨機對其中11組試驗數(shù)據(jù)與對應(yīng)的試驗結(jié)果數(shù)據(jù)進行訓練,剩下2組試驗數(shù)據(jù)用于檢驗預測結(jié)果,設(shè)最大迭代次數(shù)為180,學習率為0.2,目標誤差為1×10-5。訓練及預測結(jié)果如圖9、圖10所示。
神經(jīng)網(wǎng)絡(luò)訓練易產(chǎn)生過擬合,為驗證這種現(xiàn)象的發(fā)生概率,采用相關(guān)系數(shù)法對擬合進行評價,可知訓練樣本的擬合程度和測試樣本的擬合程度分別高達0.99986和0.99933,證明此BP神經(jīng)網(wǎng)絡(luò)訓練效果較好。
5遺傳算法尋優(yōu)
5.1柵葉結(jié)構(gòu)
優(yōu)化數(shù)學模型優(yōu)化設(shè)計數(shù)學模型包括設(shè)計目標、設(shè)計變量、約束條件[14]3個因素。為減輕攔污柵質(zhì)量,并盡量使柵葉激振頻率和固振頻率的比值與1之差的絕對值大于0.25,選取柵葉激振頻率和固振頻率的比值和柵葉的質(zhì)量作為目標函數(shù),選取柵葉寬度、長度、厚度、間距作為4個設(shè)計變量。因4個設(shè)計變量都有自己的取值范圍,故多工況離散變量優(yōu)化問題可轉(zhuǎn)化為多變量多約束優(yōu)化問題[15]。
5.2BP-GA算法尋最優(yōu)
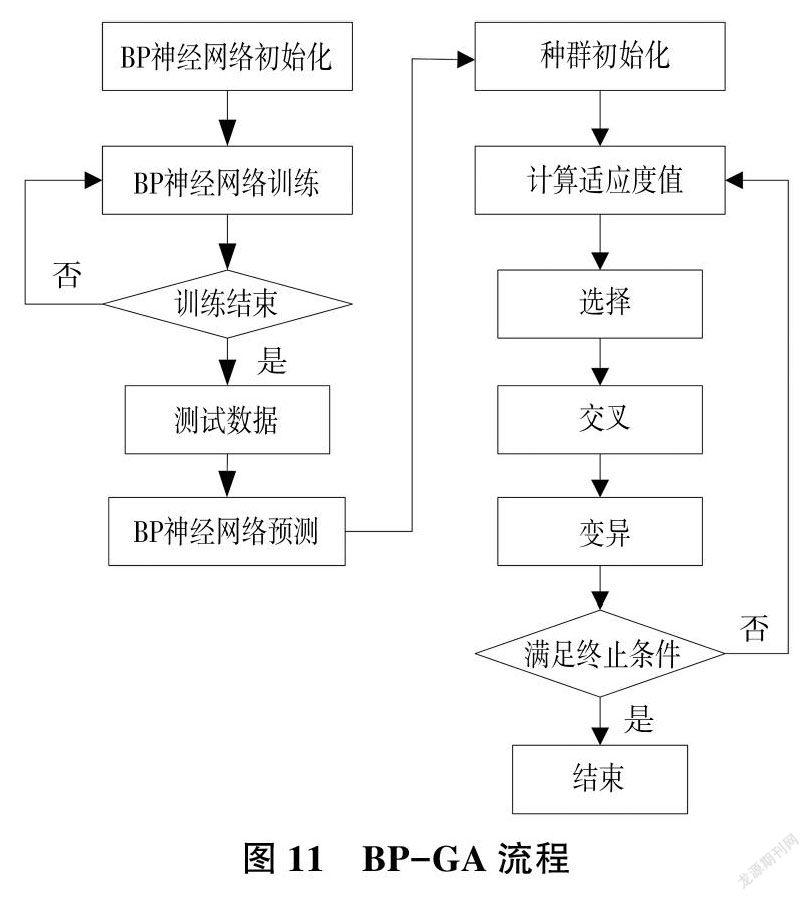
BP神經(jīng)網(wǎng)絡(luò)具有優(yōu)秀的函數(shù)逼近能力,但其一般進行局部尋優(yōu),易陷入局部最小值。遺傳算法有良好的全局尋優(yōu)能力,但其尋優(yōu)過程需要一個適應(yīng)度函數(shù),本文將BP神經(jīng)網(wǎng)絡(luò)逼近得到的非線性映射關(guān)系建立的數(shù)學模型作為遺傳算法的適應(yīng)度函數(shù)[16],實現(xiàn)了BP神經(jīng)網(wǎng)絡(luò)和遺傳算法的結(jié)合。該優(yōu)化方法的流程見圖11。
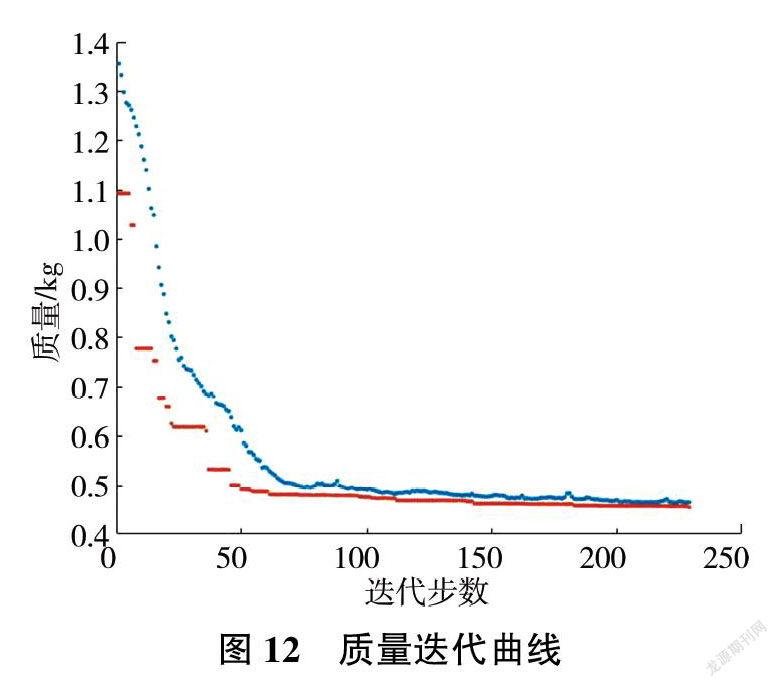
借助MATLAB平臺,設(shè)計初始種群為50,交叉算子為0.2,變異概率為0.1,最大迭代次數(shù)為230,其迭代過程如圖12所示。
圖12中上散點線為平均質(zhì)量的迭代結(jié)果,下散點線為最優(yōu)質(zhì)量的迭代結(jié)果。可知,經(jīng)過約230次迭代后計算趨于收斂,最終質(zhì)量在約束條件下穩(wěn)定于0.45kg,得出相應(yīng)的最優(yōu)設(shè)計變量見表6。
優(yōu)化后頻率比值遠離了共振的范圍,提高了振動方面的安全性,在此基礎(chǔ)上,柵葉的自重減小,提高了經(jīng)濟性。
6結(jié)論
本文對某攔污柵柵葉進行液固耦合振動分析研究,確定均勻設(shè)計試驗表,通過Fluent軟件計算各試驗下的卡門渦街激振頻率,通過模態(tài)分析計算與激振頻率相近的頻率。用BP-GA算法對試驗結(jié)果進行優(yōu)化處理,以質(zhì)量作為目標函數(shù)、以頻率比值作為約束條件,進行多次迭代求解,得出試驗結(jié)果,使得柵葉在滿足振動條件的同時自重降到最小。
【責任編輯 張華巖】

