小學數學作業優化設計策略

高香琴

（福州市長樂區營前中心小學，福建 長樂 350200）

數學作業，既是夯實學科基礎的重要手段，亦是培養學生理性思維、鍛煉其解決問題能力的有效渠道。但是一直以來，由于受到“功利性教育理念”的影響，不少一線教師在布置作業時，常常以無差別化的“題海戰術”為主，作業形式單一、內容乏善可陳、缺乏層次感和針對性。這類作業不僅無法滿足各層次學生的需要，更加重了他們的學業負擔，繼而在過量、過難的作業中喪失學科熱情和學習信心。正因如此，隨著“雙減”政策的不斷推進，如何在小學教學中有效優化學科作業質量，做到“控量減負、提質增效”，幫助學生從機械化、無效化的重復性作業中擺脫出來，［1］已經成為教育領域的研究熱點。為了落實這一目標，本文圍繞如何在“雙減”背景下優化小學數學作業設計展開探討。

一、知識遷移，凸顯作業的前導性

前導性作業是教師在授課前，鼓勵學生在預習新課的同時，嘗試運用已學知識推導新知、理解數理知識，以達到高效地吸收新課的目的。在以“生本”理念為核心的“雙減”背景下，教師可以根據學生的最近發展區，適當設計一些前導性作業，引導他們利用知識遷移，對新課內容進行自主探究，繼而在適當的“挑戰”中，獲得能力提升。值得注意的是，為避免給學生加重負擔，在設計該類作業時，教師應當遵循“量少而精”的原則，確保作業的針對性。

例如，在學習《除數是兩位數的除法》時，結合教材例題及兒童感興趣的話題，設置了以下作業：

題1 是針對除數是一位數的除法的算法與算理進行復習、強化，有助于學生新舊知識的銜接，以實現方法與技能的遷移。題2 是讓學生在掌握除數是一位數的除法的計算方法后，自主探究，嘗試計算除數是兩位數的除法，以此提升學生的推演能力。

在教學中，適當引入前導性作業，不僅能夠鞏固舊知識，還能夠引導學生在“熟悉與陌生”的中界線上，運用合情推理法，對新知展開探究，促使他們在知識遷移的過程中，真正吃透除法的算理，突破教學難點，完善學科知識結構。

二、聚焦生活，增強作業的趣味性

“數學源于生活，又應用于生活”。在小學階段的數學教學中，教師將學科作業與生活相聯系、相滲透，不僅能夠讓抽象的數學知識變得具體可感，增強學科作業的趣味性，減輕學習數學的枯燥感與畏難情緒，拉近學生與數學作業之間的心理距離；還有益于轉化學生的視角，引導他們用數學的眼光看待生活，用數學的思維解決生活問題。應用性強、趣味性高的學科作業有助于逐漸激發學生主動學習的內在驅動力。

例如，在人教版六年級“圓的面積”一課中，為切實提升作業的趣味性，深化學生對知識的理解與應用，筆者將數學知識與生活問題合理融合，以“餐桌上的數學問題”為主題，設計了以下趣味性作業：

李阿姨想給家中圓形餐桌鋪上一張桌布（桌布大小與餐桌面積一樣），她測量了三組數據：

A：桌子邊緣周長是3.768 米；

B：桌布對折一次后折痕長1.2 米；

C：桌布對折兩次后折痕長0.6 米。

1.如果你是李阿姨，你會選擇哪個數據，購買合適的桌布？說說你的理由。

2.圓形桌布是從一塊正方形的布料上剪下來的，你覺得正方形的邊長至少要多少米？剪下圓形桌布后剩下的布料是多少平方米？（請先畫出示意圖，再列式計算）

3.（1）如果在餐桌中間擺一個圓形轉盤（見圖1），轉盤的半徑尺寸有：①6.5 分米②5 分米③2 分米。你覺得選哪一種比較合適？請說明理由。

（2）李阿姨家的圓形菜盤子直徑是20 厘米，這張轉盤最多能擺下25 個盤子嗎？說說你的想法。（請動手畫一畫、擺一擺）

第1、2 小題，主要考查學生對基礎知識的掌握情況。第3 小題的第（1）問，學生根據題目提供的數據，要結合生活實際才能做出正確的選擇。第（2）問，雖然學生都能通過計算求出轉盤的面積和25 個圓盤的面積總和，但是由于部分學生缺乏一定的生活經驗，忽略了圓形之間的擺放要有空隙，即圓不能密鋪的特性，容易做出錯誤判斷。本題通過創設貼近生活、生動有趣的問題情境，充分調動學生的探究興趣，使學生感受到生活中處處有數學，培養學生樂學數學、善學數學。

三、關注差異，體現作業的層次性

遵循教育規律，以“學生為本”，是貫徹“雙減”政策的基本原則。由于個體間的思維方式、知識基礎及認知能力存在較大差異，學生的數學學科素養也有較大差距。在日常教學中，教師必須正視并尊重這種差異性，以“學習能力”為切入點，通過合理設計適量的、具有不同梯度和難度的作業，滿足各層次學生的學習需要。［2］不僅幫助學生擺脫無效的、不符合其學情的作業，還促使他們在個性化的數學作業中，逐漸強化自身的學科素養，進而落實“讓各層次個體均有所益”的施教理念。

例如，在教學《圓錐》時，為了使每個學生都能學有所得，筆者根據不同層次學生對知識的掌握情況及自身的思維水平，設計了以下一組難易有別的梯度性作業：

請根據圖2 的直角三角形，完成《圓錐》學習作業單（見表1）。

圖2

表1 《圓錐》作業單

本道題組中，因為之前在認識圓錐時，通過多媒體動態演示，學生已直觀地看到直角三角形快速旋轉形成圓錐的過程，所以大部分學生都能比較輕松地完成第1、2 兩道基礎題，既鞏固所學知識，又增強他們學習數學的自信心。題3、題4 有一定的難度，富有挑戰性，能充分激發學生的探索欲望。一些優秀的學生具有豐富的空間想象力，能想象出以斜邊為軸旋轉時形成的圖形形態——兩個有公共底的圓錐，它們以斜邊的高為底面半徑，高的和為斜邊的長。這樣有層次性的作業設計，有助于深化學生靈活運用學科知識的素養，提升他們的空間想象能力和探究精神。

教學實際中，教師秉持因材施教的理念，通過適量、適度、有彈性的分層作業，對不同層次的學生進行梯度訓練，減輕學生的作業負擔，精準提升其數學素養，進而實現優化提質、分層增效的作業設計目標。

四、發散思維，強調作業的開放性

從以往的教學經驗來看，很多教師傾向于布置一些形式單調、解法單一的單向式作業。這不僅容易讓學生陷入思維定勢與學科知識應用能力不足的困境，還有礙于其發散思維與多向思考能力的發展。在小學階段的數學教學中，為有效轉變這一現狀，教師可以適當設計一些多向發散型的開放題，引導學生在一題多解、一題多變和一題多思中，學會抓住數學本質，懂得靈活變通，突破思維慣性，進而形成多維度思考的橫縱聯想能力，以達到強化發散思維、拓寬思考廣度、提升解題能力的目的。

例如，教學《軸對稱圖形》后，為鍛煉學生的發散思維，教師設計了以下開放性作業（見圖3）：

圖3

下圖是軸對稱圖形的一半，你能用哪幾種方式補全這個軸對稱圖形，并畫出它的對稱軸？

本題的解法與思考方向具有多元化的特征，開放性較強。在具體解題過程中，學生的解法如下：

（1）根據“橫縱方向的直線為對稱軸”的常規思路，多數學生都能以線段“AD”“AB”和“BC”所在的直線為對稱軸，畫出軸對稱圖形；

（2）部分學生對上述方法進行發散拓展，補充了以斜邊“DC”為對稱軸的軸對稱圖形；

（3）個別學生突破“以現有直線作為對稱軸”的思維模式，對已有解法進行深度發散延伸。即先根據解法（1）（2）得到對稱圖，再以某一公共頂點為中心，將梯形ABCD 旋轉90°，便得到以其旋轉角的角平分線為對稱軸的軸對稱圖形。

通過開放性作業的設計，引導學生從多維度分析數學問題，從多層面探究數量關系，拓寬學生的思維廣度，強化其發散性思維與邏輯推理能力。

五、深化素養，提高作業的探究性

探究性作業是指學生在具有一定探究性的數學問題的引導下，根據自身已有的知識儲備及思考模式對知識展開探索，從而深化數學素養的一類作業。在以“學生為本位”的“雙減”背景下，為提升學生的學科素養，培養實證精神與理性思維，在日常的作業設計過程中，教師可以適當設計一些具有“探究性”的作業，引導小學生充分調動自身已有的知識經驗及思考能力，探究、發現規律，解決數學問題，培養探究素養與實踐能力。［3］

例如，在教學“長方形的周長”一課后，為培養學生的邏輯推理、數學表達、創新思考等綜合應用能力，筆者設計了以下作業：

劉大爺想用16 米長的籬笆靠墻圍成一個長方形的雞舍（如圖4），可以有幾種不同的圍法？哪種圍法的面積最大？是多少平方米？請說明理由。（雞舍的長、寬取整厘米數）

學生小組合作，采用列表法和枚舉法，把不同的圍法一一呈現（見表2）。通過對數據的觀察、分析、思考、合作交流，在教師的引導下，得出結論：（長+寬）的和一定時，長與寬的差越小，長與寬的乘積即長方形的面積就越大。

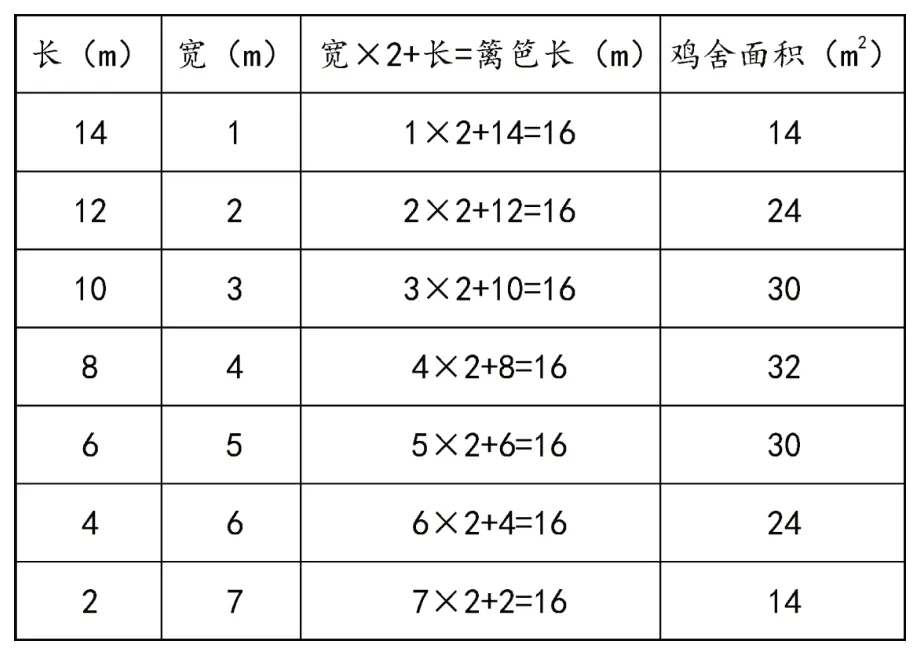
表2 不同的圍籬笆方法的數據

教學中，學生通過合作交流，共同完成實驗探究性作業，不僅有益于培養合作意識、勇于探索的實證精神，而且在切實拓展思維能力、培養思維素養方面亦有顯著成效。

在“雙減”背景下，為了提升數學課業的質量、減輕學生負擔、增強教育的實效性，教師在設計作業時，應當注重因人而異，為不同層次的學生布置適量的、符合其學情的梯度性作業。通過創新作業形式，引入前導性作業、將作業生活化以及設計具有探究意義的實踐作業等策略，以優化學科作業，貫徹“雙減”政策。