具弱界面粘結磁電彈性層合梁的非線性靜力分析

鄭玉芳, 康崇春，高杰，陳昌萍

(1. 福州大學土木工程學院，福建 福州 350108； 2. 廈門理工學院土木工程與建筑學院，福建 廈門 361024)

0 引言

磁電彈性(MEE)復合材料具有正、逆磁電效應，相比于傳統的壓電材料和壓磁材料，具有更高的磁電耦合性能. 這些材料被廣泛用于智能復合材料結構中. 同時，由于加工工藝中的不足或結構長期處于復雜的工作環境，磁電層合結構的層間界面的粘結性能容易減弱甚至完全喪失，其結果將改變結構中位移場、應力場、電勢場和磁勢場的分布，對其力學性能產生負面影響. 因此，研究具弱界面粘結磁電彈性層合梁的非線性力學行為具有重要的意義.

Wang等[1]采用狀態空間法和傳遞矩陣法，推導了多層磁電彈性圓板在簡支邊界條件下靜態響應的三維解. 朱炳任等[2]研究材料的體積分數、高跨比和非局部參數對MEE層合梁彎曲行為的影響. Chen等[3]應用漸進變分法，研究MEE層合板的非線性靜力學行為的影響. Zhang等[4]利用高階剪切變形理論和von Karman非線性應變，研究材料的疊層順序、溫度對MEE層合梁的非線性靜力學的影響. 劉寶漢等[5]采用彈簧型耦合界面模型模擬非完美界面，研究含非完美界面的雙層壓電/壓磁復合材料中裂紋尖端應力強度因子. Kuo等[6]利用微觀力學方法，研究具界面缺陷的磁電復合材料的力學行為. Kuo等[7]應用廣義線彈簧模型，研究具弱界面粘結MEE層合板的靜態行為. Kong等[8]研究非理想界面對結構的磁電耦合效應的影響. 王禾翎[9]討論了彎曲界面、裂紋和界面粘結對MEE復合材料性能的影響. 由于對受損界面間復雜的磁電耦合效應很難精確描述 , 從研究成果來看，關于具弱界面粘結磁電彈性材料結構的非線性力學研究成果相對較少.

本文基于Soldatos精確應力分析的廣義五自由度梁理論、von Karman非線性理論和Hamilton原理，通過引入靜力平衡方程、靜電和磁靜力學的Maxwell方程的通解，建立具弱界面粘結MEE層合梁的非線性平衡微分方程，利用Galerkin方法對其進行求解. 討論界面粘結強度對具弱界面粘結MEE層合梁的位移、應力、電勢和磁勢沿梁厚方向分布的影響.

1 基本方程

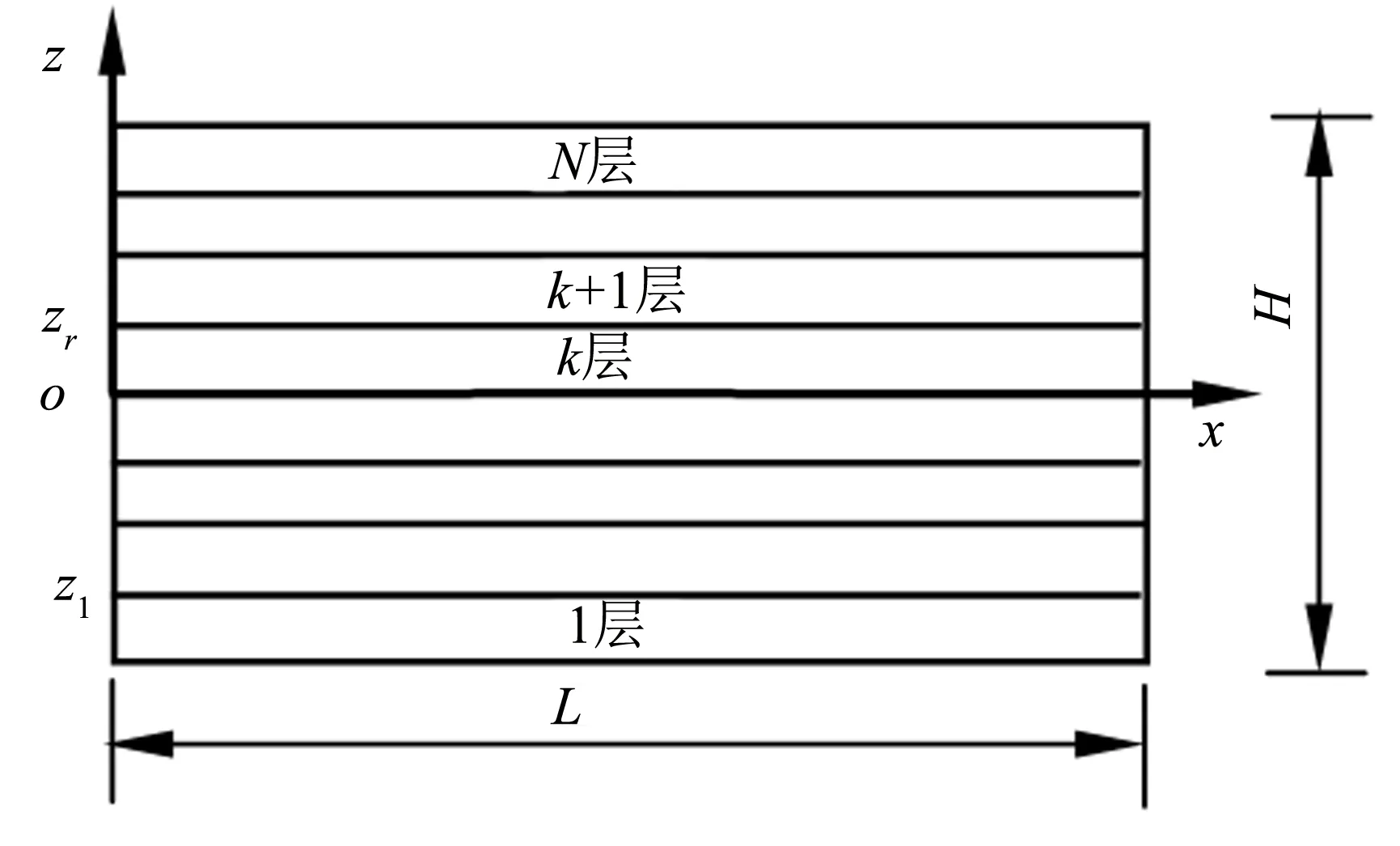
圖1 磁電彈性層合梁結構示意圖 Fig.1 Schematic diagram of magneto-electro-elastic laminated beam

如圖1所示，磁電彈性層合梁，長為L，厚度為H，由N個厚度相同的正交各向異性磁電材料單層組成.用zr(r=1，2，…，N-1)表示層合梁中第r個界面的位置，位于層合梁中第k層與第k+1層之間(k=1，2，…，N).

基于Soldatos精確應力分析的廣義五自由度梁理論[10]和層間界面剪切模型[11]，當忽略法向位移改變量，磁電彈性層合梁內任一點的位移場、電勢場和磁勢場可設為：

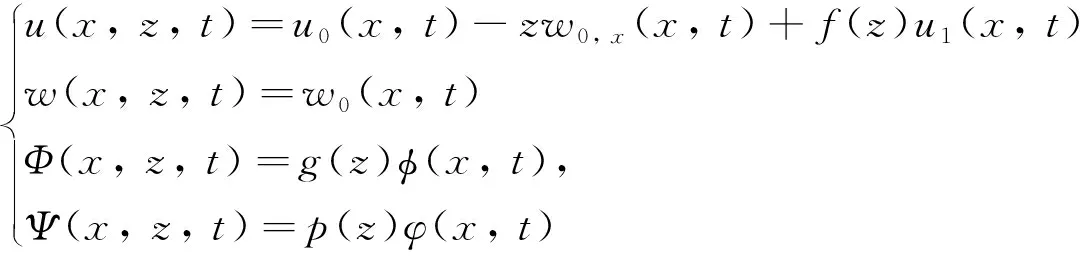
(1)

式中：u和w分別表示在x和z方向上的位移；Φ和Ψ分別表示層中的電勢和磁勢；u0和w0表示層合梁中面上相應點的位移；u1為層合梁中面上相應點的橫向應變；φ和φ為層合梁中面上相應點的電勢和磁勢，下標“, ”表示對變量求偏導.位移分布形函數f(z)、電勢分布形函數g(z)和磁勢分布形函數p(z)反映了u1、φ和φ沿z方向變化的形式，且滿足以下的約束條件[12]：

f(0)=0，g(0)=p(0)=1，f, z(0)=1，g, z(0)=1，p, z(0)=1

(2)

對于弱界面，層間應力分量τxz、電位移分量Dz和磁通量分量Bz連續，而面內位移分量u、電勢Φ和磁勢Ψ不連續.則在第r個界面，位移改變量Δu(r)、電勢改變量ΔΦ(r)和磁勢改變量ΔΨ(r)可以用待定分布形函數的不連續性給定，即

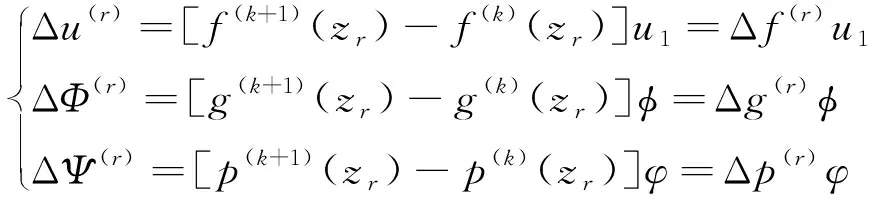
(3)

式中： 上標r(r=1，2，…，N-1)表示第r個界面；k和k+1表示與r界面有關的第k層和第k+1層.

根據von Karman幾何非線性理論，位移-應變的關系表示為：

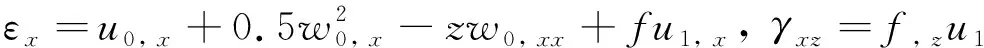
(4)

根據Maxwell理論[13]，電場強度與電勢和磁場強度與磁勢之間的關系為：

Ex=-Φ, x=-gφ, x，Ez=-Φ, z=-g, zφ，Hx=-Ψ, x=-pφ, x，Hz=-Ψ, z=-p, zφ

(5)

第k層正交各向異性磁電彈性材料的本構關系為：

(6)

式中：σx和τxz為應力分量；εx和γxz為應變分量；Di和Bi分別為電位移分量和磁通量分量；cij、eij、εij、qij、dij和μij分別為彈性系數、壓電系數、介電系數、壓磁系數、磁電系數和磁導率.

在界面粘結強度變弱的初始階段，設弱界面具有以下的線性非耦合性質[14]，即

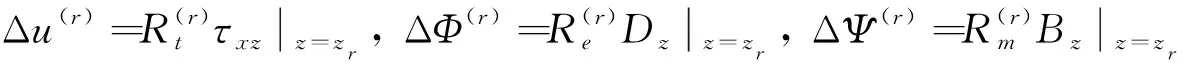
(7)

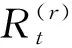
根據Hamilton變分原理，得：

式中：A為中面面積；q為梁承受的橫向載荷，且取q(x)=q0sin(πx/L).

由式(7)和(8)，得到具弱界面粘結MEE層合梁的非線性控制平衡方程為

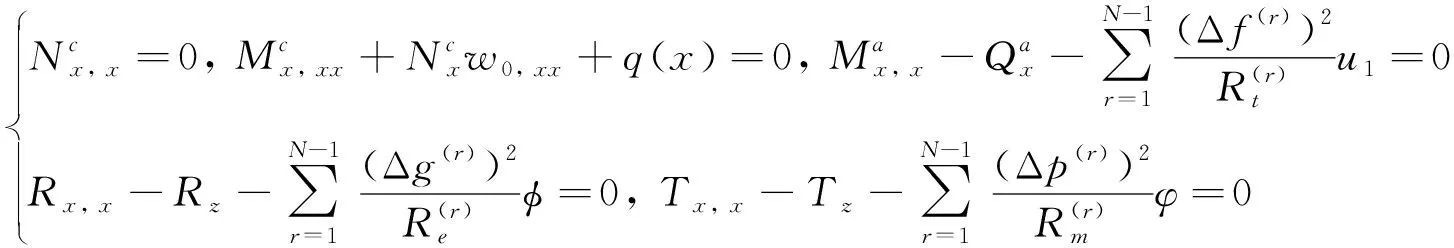
(9)

式中：

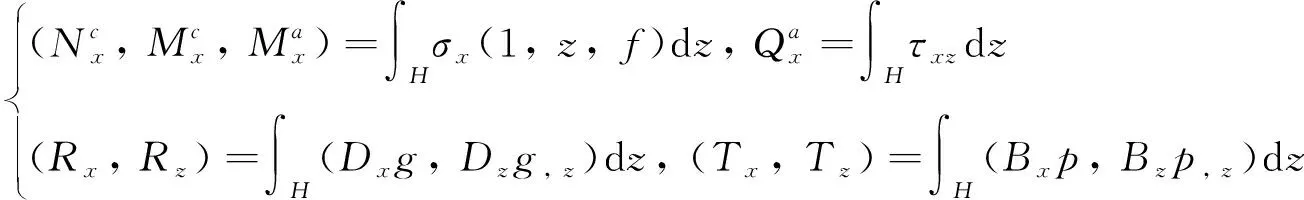
(10)

引入如下的無量綱參數：

(11)

式中： 對于材料不同的多層梁，cmax、emax、εmax、qmax、dmax和μmax為各種材料中彈性剛度系數、壓電系數、介電系數、壓磁系數、磁電系數和磁導率的最大值.

將式(4)、式(6)和式(10)代入式(9)，并應用式(11)，得到具弱界面粘結MEE層合梁的無量綱非線性控制方程為：

(12)

式中：

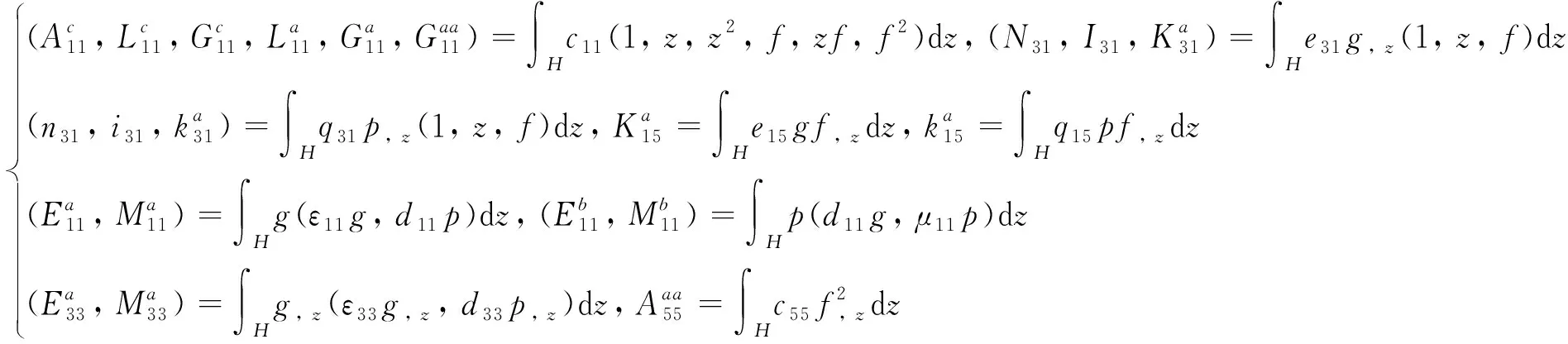
(13)

2 具弱界面粘結簡支磁電彈性層合梁的形函數

由于界面的復雜性，一般研究假設界面本構關系具有線性非耦合的性質，忽略非線性項的影響[14-15]. 第k層梁的待定形函數f(z)、g(z)和p(z)應滿足應力表示的平衡方程、靜電和磁靜力學的Maxwell方程，即

σx, x+τxz, z=0，Dx, x+Dz, z=0，Bx, x+Bz, z=0

(14)

設u0,u1,w0,φ和φ為以下滿足簡支可動邊界條件的位移模式：

(u0,u1)=(A1,A3)cos(αx), (w0,φ,φ)=(A2,A4,A5)sin(αx),α=π/L

(15)

將式(15)代入式(14)，并利用式(4)～(6)，得:

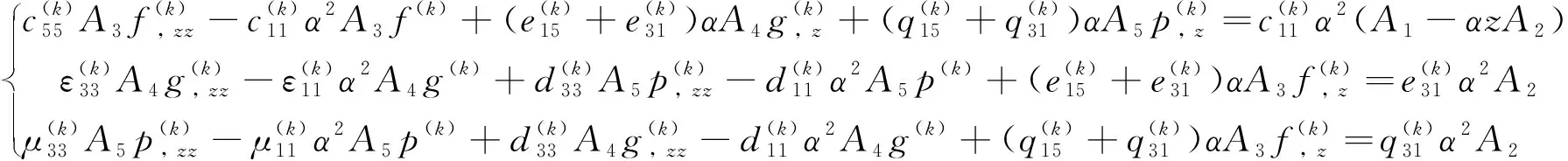
(16)

假設待求形函數為：

F(k)(z)=A3f(k)(z),G(k)(z)=A4g(k)(z)，P(k)(z)=A5p(k)(z)

(17)

式(16)可以看成關于待求形函數F(k)(z)、G(k)(z)和P(k)(z)的二階常系數非齊次線性微分方程組，方程組的解由滿足齊次線性微分方程組的通解和一個滿足方程組的特解組成.通過消元法可求得齊次線性微分方程組的通解和通過待定系數法得到非齊次線性微分方程組的特解，則第k層待定形函數可以表示為：

(18)

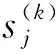
m1λ6+m2λ4+m3λ2+m4=0

式中：

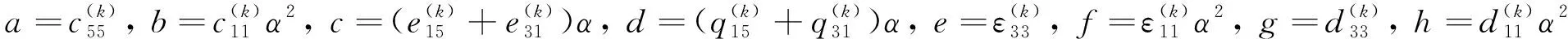
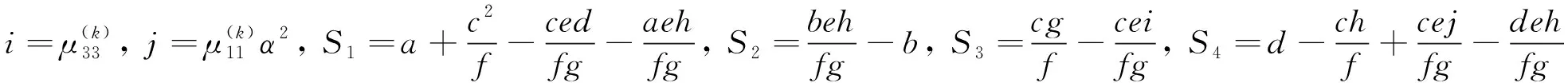
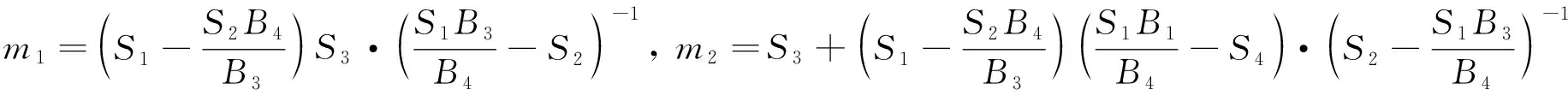
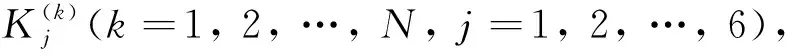
對于弱界面粘結條件下，界面處剪應力τxz、電位移Dz和磁通Bz在各層界面處連續，即

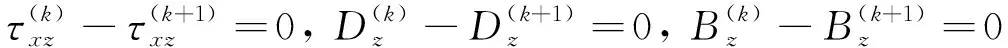
(19)

應用式(4)、式(5)、式(6)、式(15)和式(18)，得到：

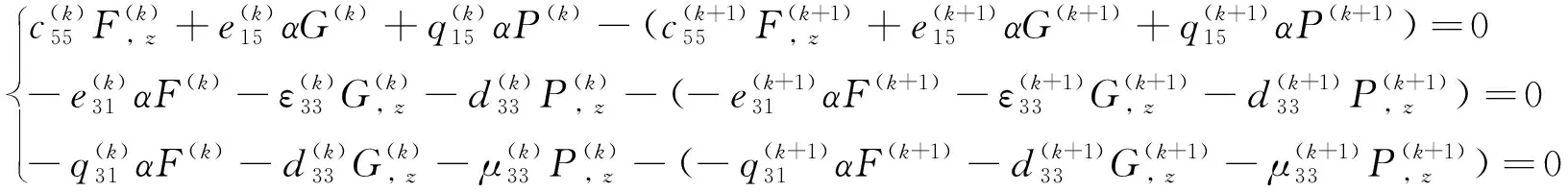
(20)

對于弱界面粘結條件下，界面處位移u、電勢Φ和磁勢Ψ不連續，應用式(3)、式(7)、式(15)和式(18)，得到：

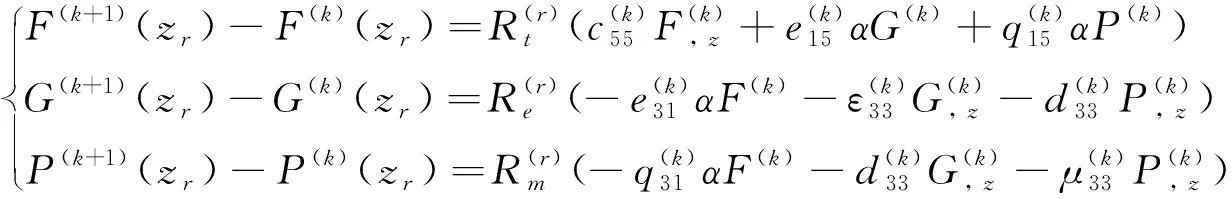
(21)

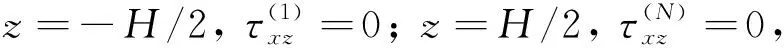
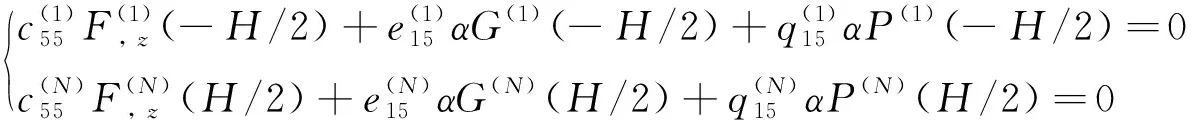
(22)

由磁電條件得，在閉路條件下：

Φ(1)|z=-H/2=Φ(N)|z=H/2=0,Ψ(1)|z=-H/2=Ψ(N)|z=H/2=0

(23)

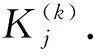
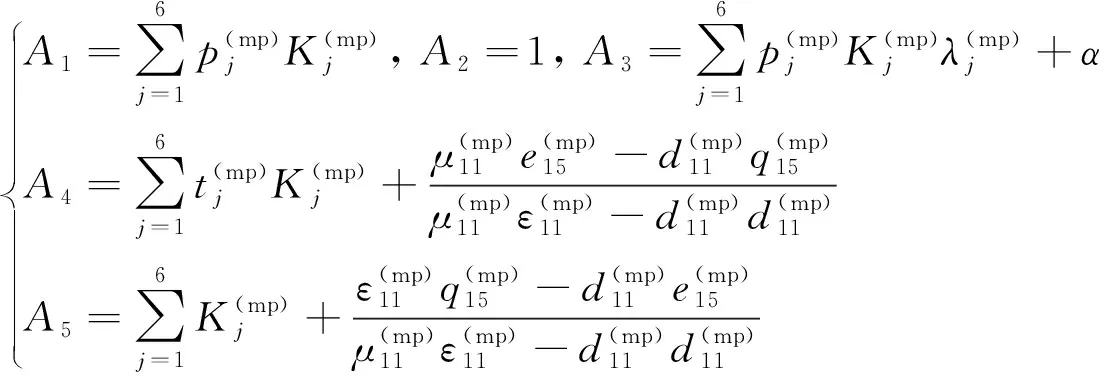
(24)

式中： 上標“mp”表示中性層(z=0)所在的第k(mp)層梁. 由式(18)和式(24)可得到形函數f(k)(z)、g(k)(z)和p(k)(z)的表達式.

3 數值結果與討論

對于兩端簡支的磁電彈性層合梁，選取的位移、電勢和磁勢的解為：

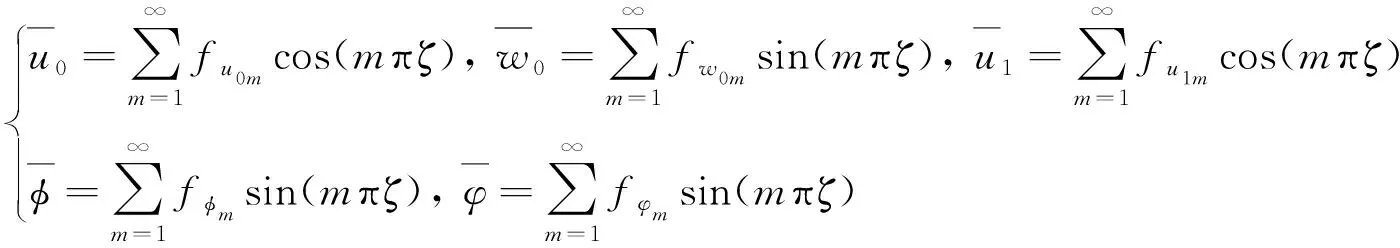
(25)

將式(25)代入非線性平衡方程(12)，應用Galerkin方法，并取一階截斷，則非線性微分方程組轉化為含有fu0、fw0、fu1、fφ和fφ的非線性代數方程組進行求解.

為了驗證本文模型和方法的正確性，將本文模型退化為理想界面的磁電彈性層合梁結構(BaTiO3/CoFe2O4)，并取文獻[13]中的材料參數和幾何參數. 圖2和圖3分別給出了兩端簡支磁電彈性層合梁中點電勢和磁勢沿厚度的變化規律，并與文獻[13]中的數值結果進行對比. 從圖中可以看出，本文得到的數值解與文獻的數值解吻合較好，驗證了本文模型和方法的正確性.

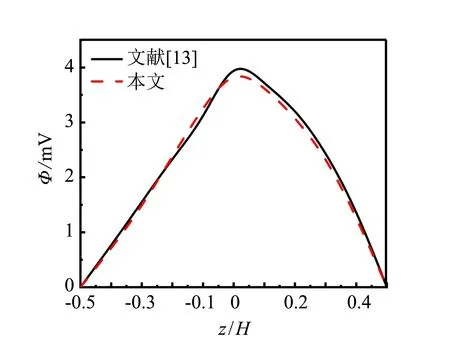
圖2 電勢Fig.2 Electric potential

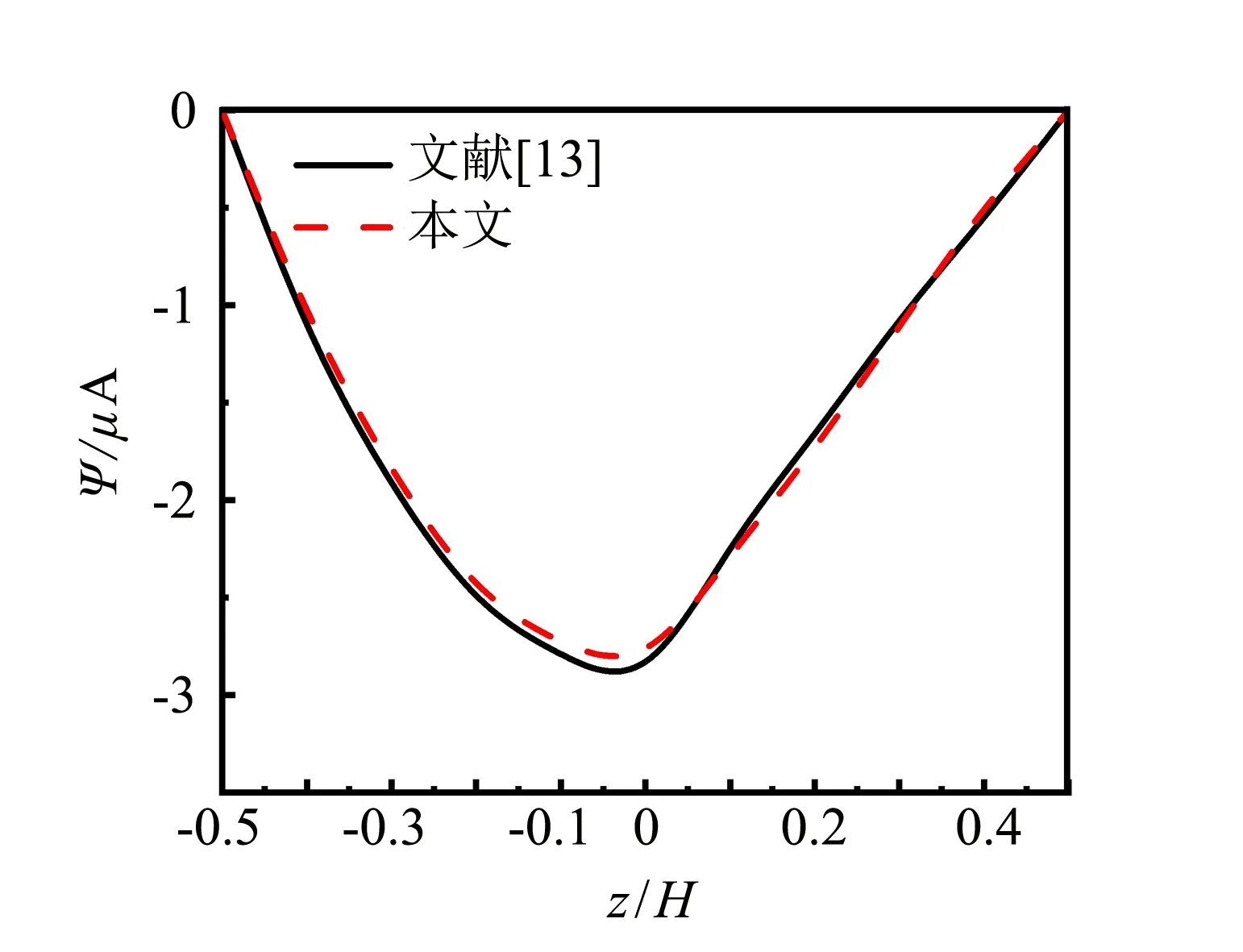
圖3 磁勢Fig.3 Magnetic potential

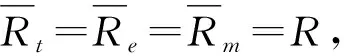
BaTiO3：c11=166 GPa，c55=43 GPa,e31=-4.4 C·m-2，e15=11.6 C·m-2,q31=0，q15=0，

d11=0,ε11=11.2×10-9F·m-1，ε33=12.6×10-9F·m-1,d33=0，

μ11=5×10-6Ns2·C-2，μ33=10×10-6Ns2·C-2

CoFe2O4:c11=286 GPa，c55=45.3 GPa,e31=0,e15=0,q31=580 N·(A·m)-1，

q15=550 N·(A·m)-1,ε11=0.08×10-9F·m-1,ε33=0.093×10-9F·m-1,

d11=0,d33=0,μ11=-590×10-6Ns2·C-2,μ33=157×10-6Ns2·C-2

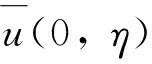
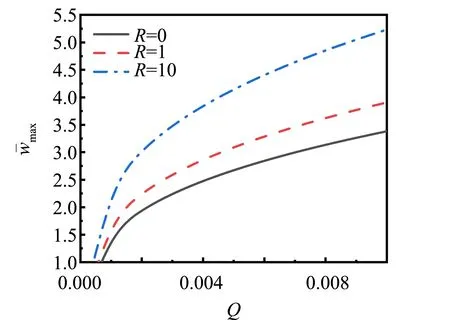
圖4 弱界面對梁中點撓度的影響Fig.4 Effect of the weak interface on the middle

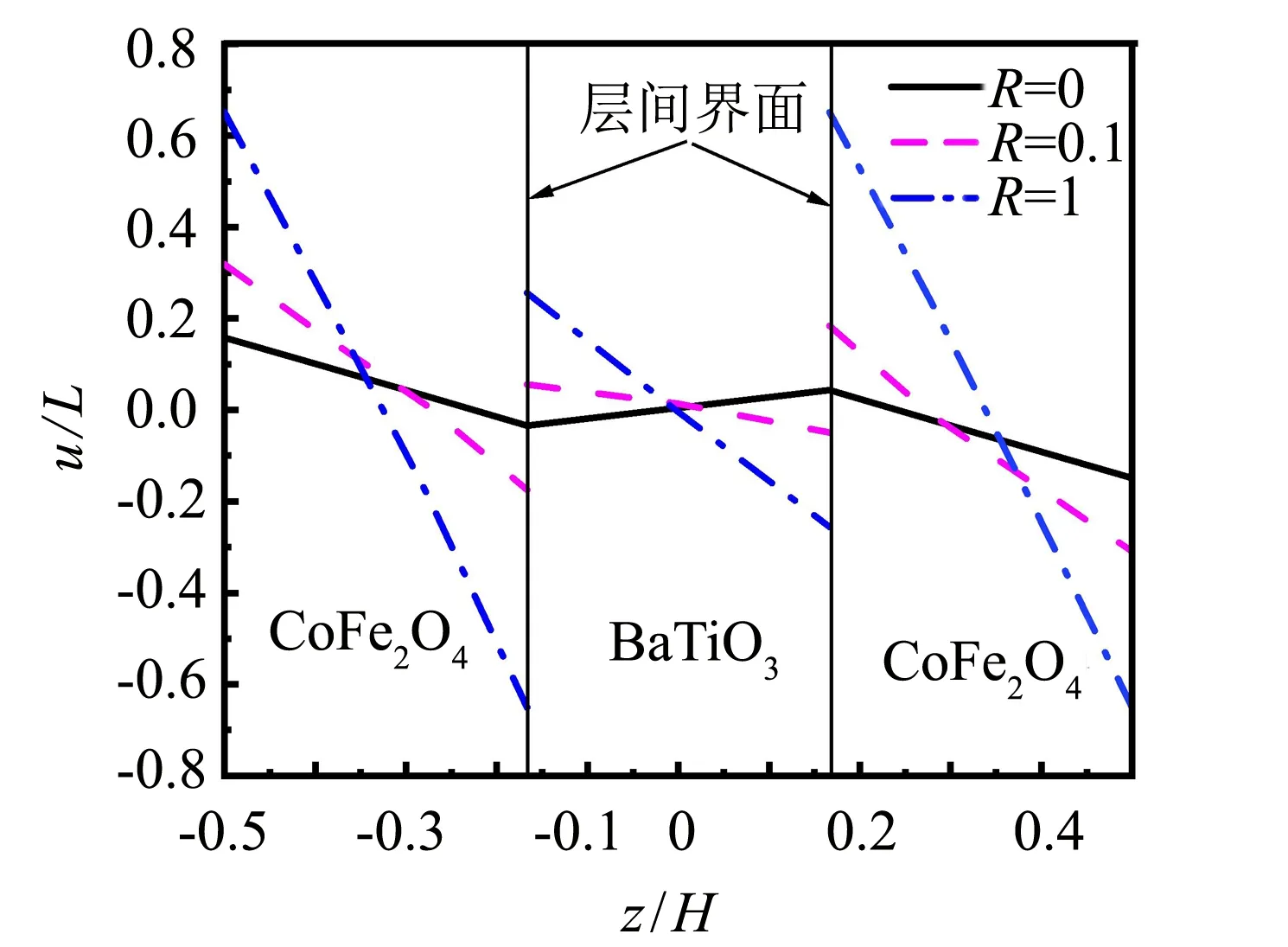
圖5 弱界面對位移的影響Fig.5 Effect of the weak interface on

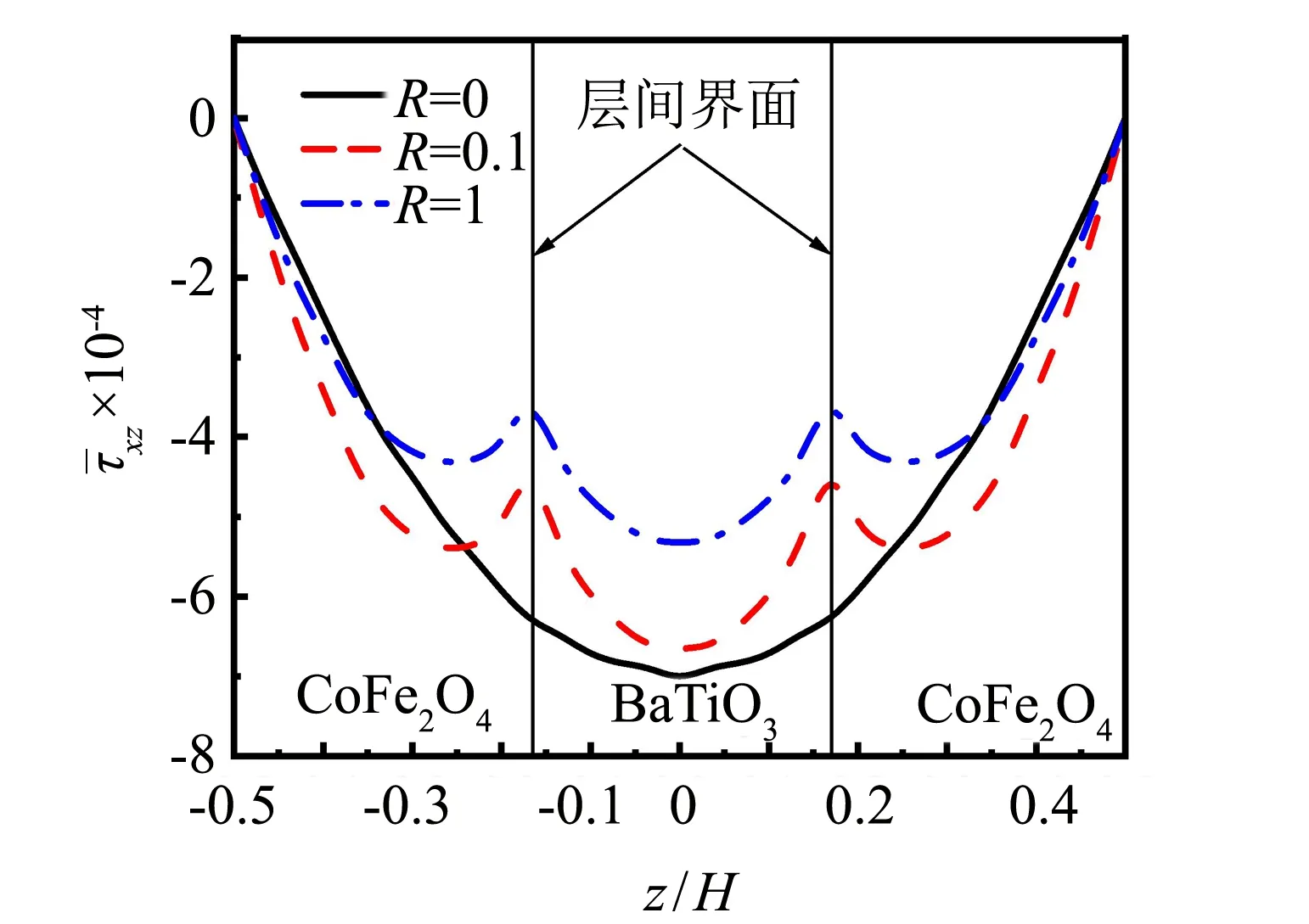
圖6 弱界面對剪應力的影響Fig.6 Effect of the weak interface on the shear stress (0, η)

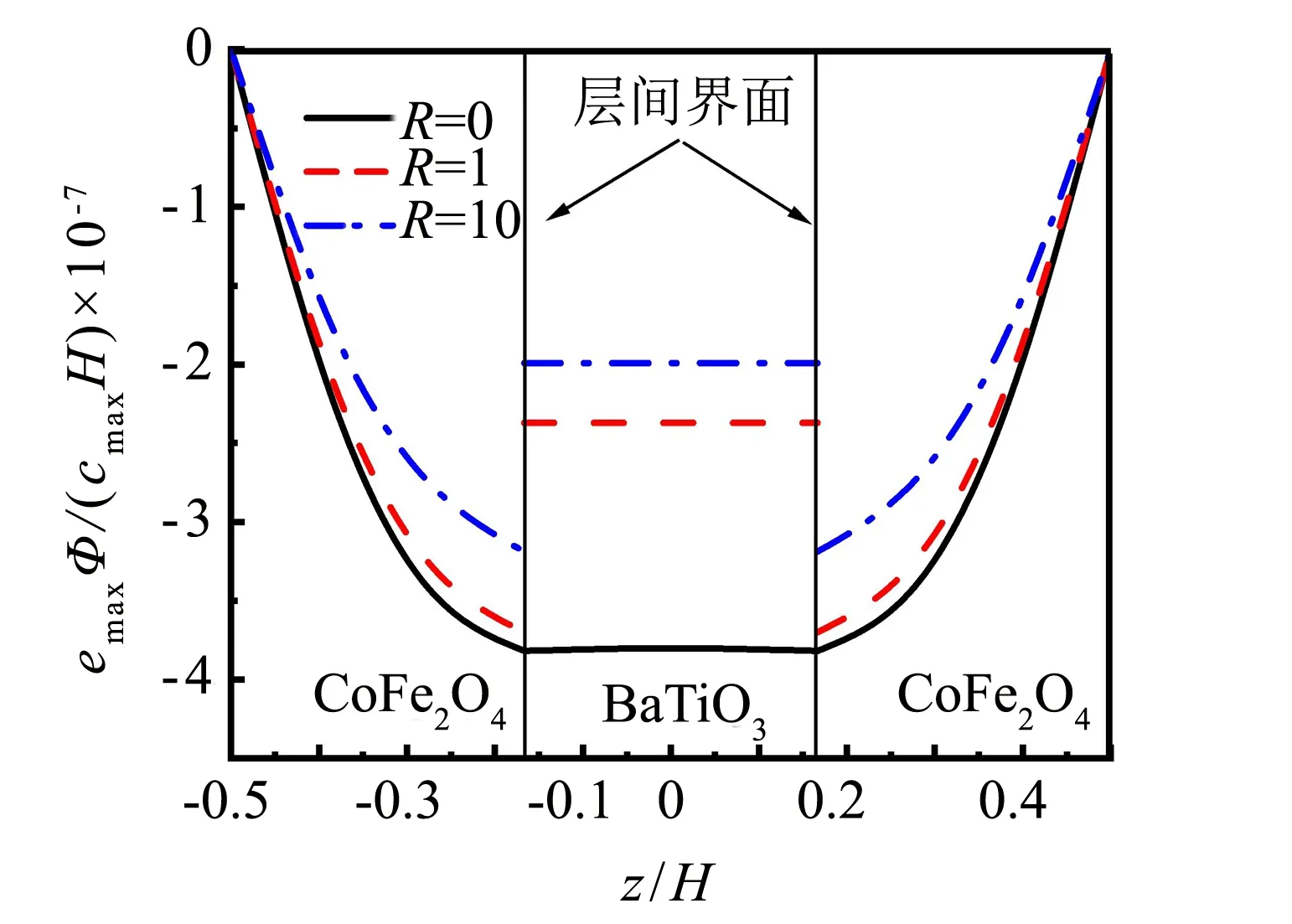
圖7 弱界面對電勢的影響Fig.7 Effect of the weak interface on

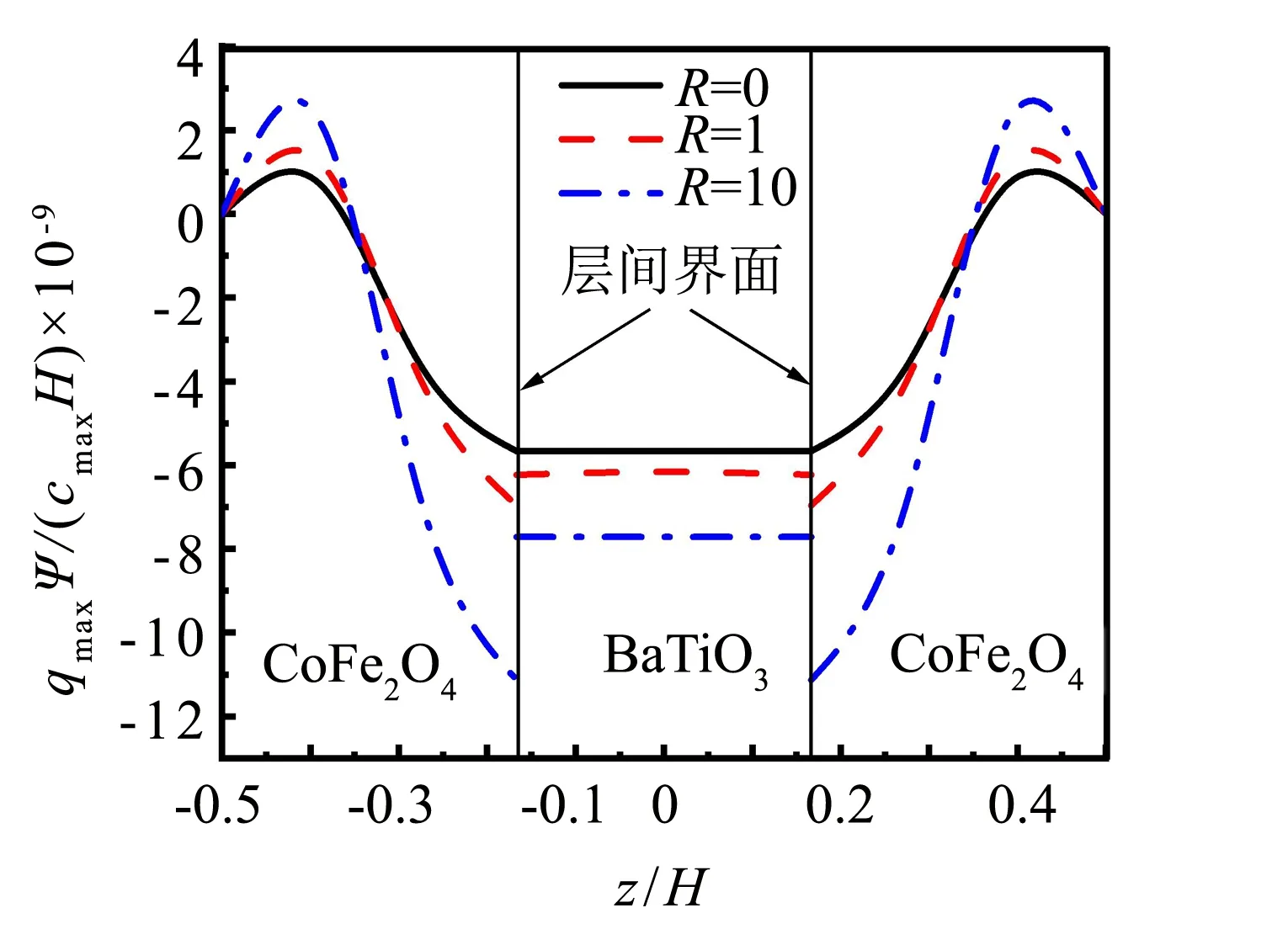
圖8 弱界面對磁勢的影響Fig.8 Effect of the weak interface on

4 結語

1) 在一定條件下，隨著界面粘結強度的減弱，磁電彈性層合梁的整體剛度減小，非線性位移越來越大，界面處的剪應力減小，且界面處的位移場在界面處出現不連續的跳躍現象，弱界面粘結改變了結構中的位移場和應力場的分布.

2) 在一定條件下，隨著界面粘結強度的減弱，界面傳遞應變的能力下降，磁電耦合效應減弱，導致界面處的電勢和磁勢出現不連續的跳躍現象，弱界面粘結改變了結構中的電勢場和磁勢場分布.

3) 在一定條件下，隨著外部荷載的增大，結構的變形加大； 弱界面粘結強度的減弱，在一定程度上減弱了磁電彈性層合梁的磁電耦合效應，且非線性特征更加明顯.