巧用“一線三等角” 模型突破幾何壓軸難題
劉敏


摘要:《義務教育數學課程標準(2022年版)》中提出,在初中階段核心素養的主要表現包含幾何直觀和模型觀念.這就要求學生能夠感知各種幾何圖形及其組成元素,依據圖形的特征進行分類,再根據形與數的聯系,構建數學問題的直觀模型.本文中抓住數學問題中常見的“一線三等角”進行研究分析,探究其在各類型問題中所表現出來的特征,從而更好地為提高學生解題能力,提升學生核心素養奠定基礎.
關鍵詞:一線三等角;模型;幾何直觀
1 引出問題
2022年安徽中考試題中有這樣一道試題:如圖1,四邊形ABCD是正方形,點E在邊AD上,△BEF是以E為直角頂點的等腰直角三角形,EF,BF分別交CD于點M,N,過點F作AD的垂線交AD的延長線于點G.連接DF,則∠FDG=°.
根據題意可以發現,在直線AD上,存在三個直角,∠A=∠BEF=∠G(或者∠A=∠BEF=∠EDM),出現這種情況,我們往往稱之為“一線三直角”的數學模型,從而利用兩個三角形全等或者相似即可.此題可根據“AAS”證△ABE≌△GEF,得出EG=AB,GF=AE,進而推出DG=GF.即可得出∠FDG的度數.
若將“一線三直角”模型中的直角改為其他角度,這樣就形成了“一線三等角”的數學模型,在解答相關問題的過程中,很容易考慮到全等三角形或者相似三角形的判定.熟練把握“一線三等角”的相關特點,感悟其在全等或者相似三角形判定中的重要作用,便于引導學生在解答過程中快速掌握利用基本圖形來描述或者分析、解決問題,從而培養學生的幾何直觀能力.
2 “一線三等角”在全等形問題中的應用
例1閱讀下面的相關材料,并回答問題.
模型學習:如圖2,∠BAD=90°,AB=AD,BC⊥AC于點C,DE⊥AC于點E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D;又∠ACB=∠AED=90°,可以通過推理得到△ABC≌△DAE,進而得到AC=,BC=.我們把這個數學模型稱為“一線三等角”模型.
模型應用:如圖3,△ABC為等邊三角形,BD=CF,∠EDF=60°,求證BE=CD.
在“模型學習”中根據這種模型的特點,可以直接判斷,由“AAS”可證△ABC≌△DAE,可得AC=DE,BC=AE;對于“模型應用”,根據條件可以發現∠B=∠C=∠EDF=60°,符合“一線三等角”的特征,故由“AAS”可證△BDE≌△CFD,從而可證明得到BE=CD.
3 “一線三等角”在相似形問題中的應用
例2如圖4,D為△ABC的內心,點E在AC上,且AD⊥DE,若DE=2,AD=CE=3,試求AB的長.
通過審題發現,題干中有內心,還有垂直,問題的目標AB與條件AD,CE分屬三條直線.因此可以考慮延長DE看是否可以構建“一線三等角”.于是延長ED交AB于點F,連接BD,如圖5,將線段AB分為AF和BF兩部分,分別計算.顯然,根據條件很容易證明△ADE≌△ADF,利用勾股定理求得AE的長度,即為AF的長度.再根據△ADE≌△ADF,可以得到∠AFD=∠AED,故有∠BFD=∠CED.利用三角形內角和可推理計算得到∠ABD=∠CBD=∠CDE,從而可得到△BFD∽△DEC,再利用相似,列比例式求得BF.BF與AF相加即可求得AB.
4 “一線三等角”在一次函數中的應用
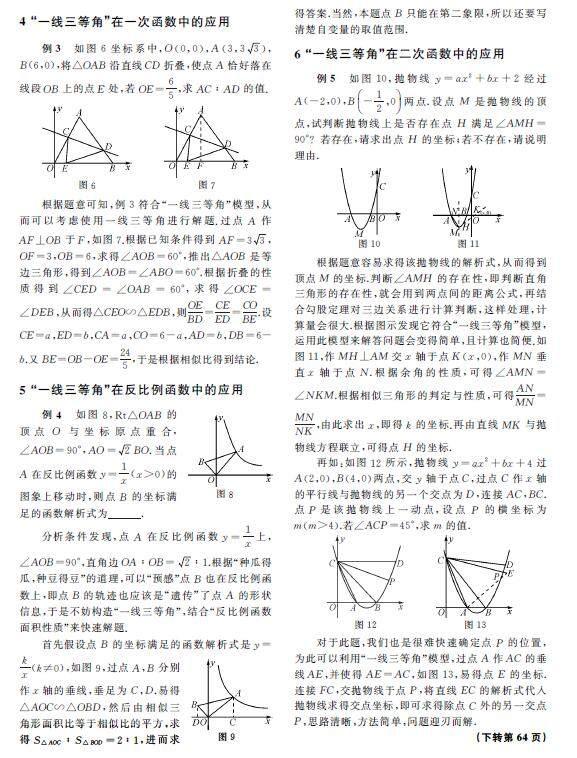
例3如圖6坐標系中,O(0,0),A(3,33),B(6,0),將△OAB沿直線CD折疊,使點A恰好落在線段OB上的點E處,若OE=65,求AC∶AD的值.
根據題意可知,例3符合“一線三等角”模型,從而可以考慮使用一線三等角進行解題.過點A作AF⊥OB于F,如圖7.根據已知條件得到AF=33,OF=3,OB=6,求得∠AOB=60°,推出△AOB是等邊三角形,得到∠AOB=∠ABO=60°.根據折疊的性質得到∠CED=∠OAB=60°,求得∠OCE=∠DEB,從而得△CEO∽△EDB,則OEBD=CEED=COBE.設CE=a,ED=b,CA=a,CO=6-a,AD=b,DB=6-b.又BE=OB-OE=245,于是根據相似比得到結論.
5 “一線三等角”在反比例函數中的應用
例4如圖8,Rt△OAB的頂點O與坐標原點重合,∠AOB=90°,AO=2BO.當點A在反比例函數y=1x(x>0)的圖象上移動時,則點B的坐標滿足的函數解析式為.
分析條件發現,點A在反比例函數y=1x上,∠AOB=90°,直角邊OA∶OB= 2∶1.根據“種瓜得瓜,種豆得豆”的道理,可以“預感”點B也在反比例函數上,即點B的軌跡也應該是“遺傳”了點A的形狀信息,于是不妨構造“一線三等角”,結合“反比例函數面積性質”來快速解題.
首先假設點B的坐標滿足的函數解析式是y=kx(k≠0),如圖9,過點A,B分別作x軸的垂線,垂足為C,D.易得△AOC∽△OBD,然后由相似三角形面積比等于相似比的平方,求得S△AOC∶S△BOD=2∶1,進而求得答案.當然,本題點B只能在第二象限,所以還要寫清楚自變量的取值范圍.
6 “一線三等角”在二次函數中的應用
例5如圖10,拋物線y=ax2+bx+2經過A(-2,0),B-12,0兩點.設點M是拋物線的頂點,試判斷拋物線上是否存在點H滿足∠AMH=90°?若存在,請求出點H的坐標;若不存在,請說明理由.
根據題意容易求得該拋物線的解析式,從而得到頂點M的坐標.判斷∠AMH的存在性,即判斷直角三角形的存在性,就會用到兩點間的距離公式,再結合勾股定理對三邊關系進行計算判斷,這樣處理,計算量會很大.根據圖示發現它符合“一線三等角”模型,運用此模型來解答問題會變得簡單,且計算也簡便.如圖11,作MH⊥AM交x軸于點K(x,0),作MN垂直x軸于點N.根據余角的性質,可得∠AMN=∠NKM.根據相似三角形的判定與性質,可得ANMN= MNNK,由此求出x,即得k的坐標.再由直線MK與拋物線方程聯立,可得點H的坐標.
再如:如圖12所示,拋物線y=ax2+bx+4過A(2,0),B(4,0)兩點,交y軸于點C,過點C作x軸的平行線與拋物線的另一個交點為D,連接AC,BC.點P是該拋物線上一動點,設點P的橫坐標為m(m>4).若∠ACP=45°,求m的值.
對于此題,我們也是很難快速確定點P的位置,為此可以利用“一線三等角”模型,過點A作AC的垂線AE,并使得AE=AC,如圖13,易得點E的坐標.連接FC,交拋物線于點P,將直線EC的解析式代入拋物線求得交點坐標,即可求得除點C外的另一交點P,思路清晰,方法簡單,問題迎刃而解.
7 “一線三等角”在圖形變換中的應用
例6等邊△ABC邊長為6,P為BC邊上一點,∠MPN=60°,且PM,PN分別于邊AB,AC交于點E,F.如圖14所示,若點P在BC邊上運動,且∠MPN繞點P旋轉,當CF=AE=2時,求PE的長.
根據題意,△ABC是等邊三角形,∠MPN=60°,可知∠B=∠C=∠MPN,符合“一線三等角”模型.因此可以考慮使用該模型下的解題基本思路.通過證明△BPE∽△CFP,根據相似三角形對應邊的比相等,再設BP=x,則CP=6-x,即可求得BP的長,進而求得PE的長.
8 “一線三等角”在動態問題中的應用
如圖15和圖16,在△ABC中,AB=AC,BC=8,tan C=34.點K在AC邊上,點M,N分別在AB,BC上,且AM=CN=2.點P從點M出發沿折線MB-BN勻速移動,到達點N時停止;而點Q在AC邊上隨P移動,且始終保持∠APQ=∠B.在點P處設計并安裝一掃描器,按定角∠APQ掃描△APQ區域(含邊界),掃描器隨點P從M到B再到N共用時36 s.若AK=94,請直接寫出點K被掃描到的總時長.
動態問題,往往作為數學試卷中的壓軸題,對學生來說此類問題難度很大,根據AB=AC,∠APQ=∠B,可以判斷出該問題所考查的是“一線三等角”模型,從而對于解題也就心中有數了,起碼為下一步的解答找到了突破口,抓住這一切入點,利用關聯三角形的相似,判斷得到△ABP∽△PCQ,則有ABPC= BPCQ,再根據題干具體要求分析研究,進而求解本題答案.
通過上述問題的研究,可以感受“一線三等角”模型在各個知識背景下的應用.借助構造一線三等角模型解題的基本手段,從復雜的圖形中分離出基本圖形,具有將問題化繁為簡的效果,同時可以幫助我們在解題中快速找到解決問題的突破口.當然,希望“一線三等角”模型能起到拋磚引玉的作用,更希望學生能形成比較完善的知識儲備,從而提高基本圖形的敏銳觀察力,以及不斷提升幾何直觀能力和問題建模思想.

