基于側向干擾的雷達對抗無人機弧形向心航線研究

王耀北，湯亞波，楊 儉

(國防科技大學，安徽 合肥 230037)

0 引 言

陸航直升機以其優越的機動性、強大的火力、超低空飛行能力實現了對敵地面目標的連續突擊，且取得了很好的作戰效益。但隨著世界各國防空武器系統的發展，陸航直升機在作戰中也越來越多地面臨敵方各種近程防空武器的挑戰，空中突防也愈加困難。為此，需要針對掩護陸軍航空兵突防問題，從雷達對抗無人機作戰特點出發，積極開展雷達對抗無人機的掩護航線規劃方法研究。

1 問題描述

雷達對抗無人機是裝載有雷達對抗偵察、干擾設備的電子對抗無人機。通過對敵方防空系統中武器控制雷達的持續壓制，可以有效掩護陸航直升機成功突防至預定作戰區域。

受機載天線工作頻段、重量、體積、安裝方式等綜合條件限制，雷達對抗無人機可采用側向干擾方式對敵雷達實施干擾，即其干擾輻射空域覆蓋范圍集中在機身兩側。如圖1中，雷達對抗無人機采用側向干擾方式，機載干擾天線水平方向的干擾輻射空域角度(干擾天線主瓣波束寬度)為2，即干擾輻射空域沿機身橫軸方向對稱分布。

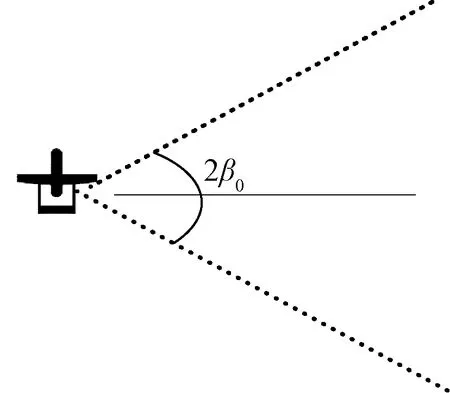
圖1 雷達對抗無人機側向干擾輻射空域示意圖

圖2為基于側向干擾的雷達對抗無人機掩護陸軍航空兵突防示意圖。圖中，敵防空系統武器控制雷達位于點，為敵方近程防空系統最大毀傷半徑。當陸航直升機從點進入以為圓心、為半徑的扇形區域中,就會被敵方雷達探測并遭到敵防空武器的直接毀傷。上述扇形區域即為陸航直升機的威脅區域。

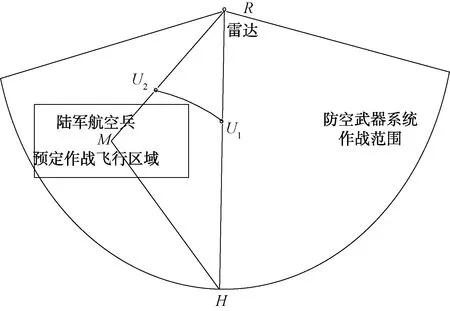
圖2 基于側向干擾的雷達對抗無人機掩護陸軍航空兵突防示意圖

假設陸航直升機突防時進入威脅區域的起始點為，要到達的威脅區域內的目標點為。陸航直升機沿直線航路突防，即線段即為需要掩護的直升機突防航線線段。這樣，本文所述的基于側向干擾的雷達對抗無人機掩護陸軍航空兵突防問題可描述為：在和之間分別選取2個點、，作為雷達對抗無人機掩護航線的起點和終點，在這2點之間規劃掩護航線，通過有效干擾，實時掩護沿航線上飛行的陸航直升機。

2 雷達干擾方程與有效掩護距離

有效掩護距離是雷達對抗無人機的重要性能指標，是研究雷達對抗無人機掩護陸軍航空兵突防航線規劃的重要依據，可以從干擾方程出發進行推導。

2.1 雷達干擾方程

雷達干擾方程是描述雷達、干擾機以及被掩護目標之間的空間電磁能量關系的數學表達式，是研究雷達對抗無人機掩護陸航直升機航線規劃方法的基礎。結合圖3給出的側向干擾條件下雷達對抗無人機、雷達和陸航直升機的空間關系示意圖，雷達干擾方程一般可表示為：

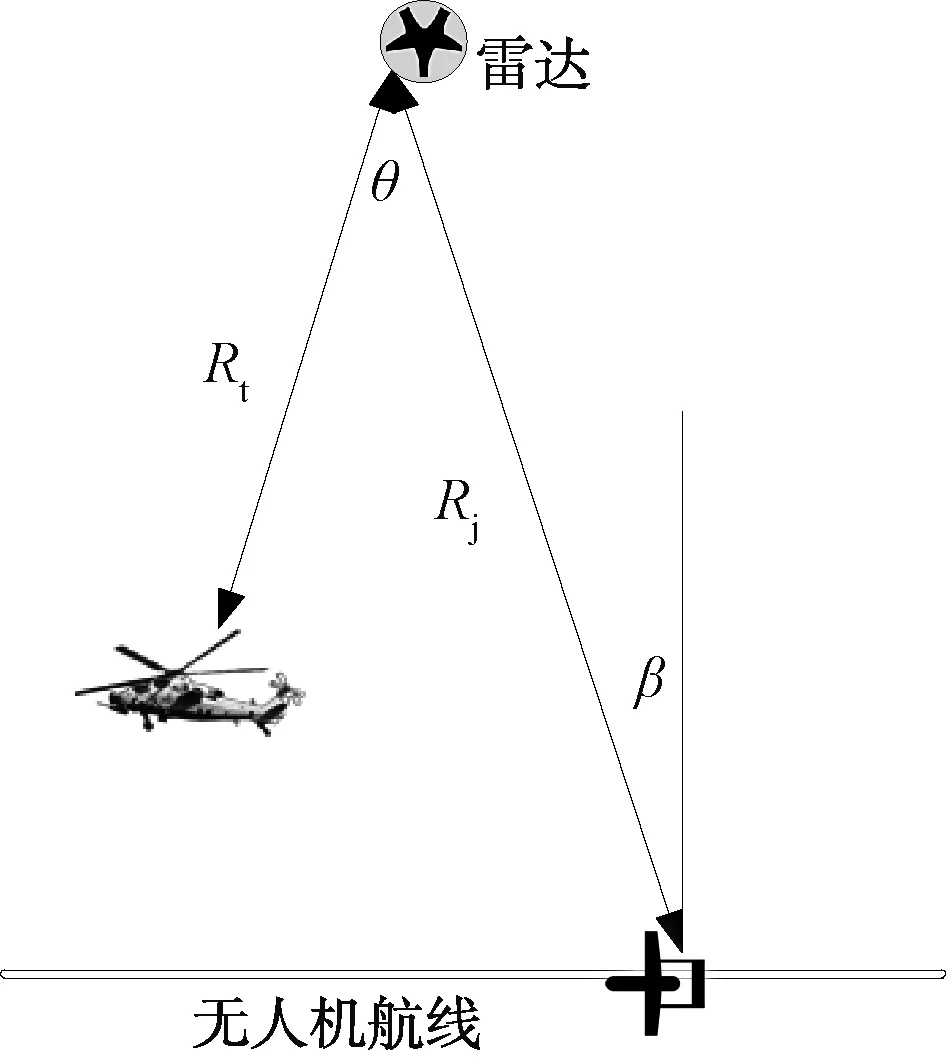
圖3 雷達對抗無人機、雷達和陸航直升機的空間關系示意圖

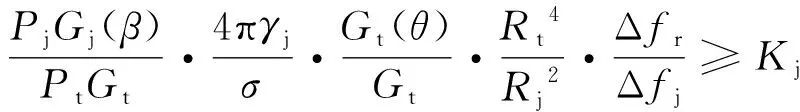
(1)

式中：為雷達的發射功率；為雷達天線主瓣方向的增益；為干擾機的發射功率；為干擾方向與干擾天線主瓣輻射方向的夾角；()為干擾機天線在干擾方向上的增益；為干擾信號對雷達天線的極化損失；為突防飛機的雷達反射截面積；是指雷達到目標的距離即掩護距離；是干擾機到雷達的距離即干擾距離；為干擾方向與雷達天線主瓣輻射方向的夾角；()為雷達天線在干擾方向上的增益；為壓制系數；Δ和Δ分別為雷達接收機和機載干擾信號的頻帶寬度。

2.2 有效掩護距離

令05為雷達天線的主瓣寬度，當≤05/2時，雷達對抗無人機可實施主瓣干擾，有()=；若≤，則雷達始終位于圖1所示的無人機干擾輻射空域(2)范圍內，有()=，為干擾天線主瓣增益。從而，可以由式(1)推導出：

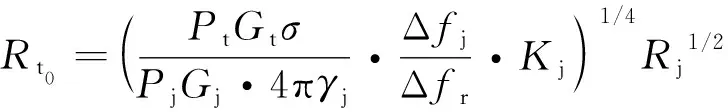
(2)

式中：t為、等相關參數給定后，根據當前雷達與無人機之間干擾距離，計算獲得的有效掩護距離。當雷達與陸航直升機之間的距離大于t時，將可以實現有效掩護。

3 雷達對抗無人機有效掩護陸航直升機突防條件分析

要實現有效掩護，當陸航直升機在突防航段上飛行時，雷達對抗無人機必須能夠實時全程干擾壓制敵方雷達。根據式(2)及推導條件，若規劃出的雷達對抗無人機任務航線能夠同時滿足以下3點，則可以實現有效掩護陸航直升機突防：

條件1：≤，即全程滿足始終將雷達納入機載雷達干擾機的干擾覆蓋空域范圍內。

條件2：≤/2，全程滿足機載干擾機對敵雷達實施主瓣干擾，即全程保持雷達、陸航直升機和無人機近似“三點一線”。

條件3：≥t，各時刻滿足陸航直升機與雷達之間的距離，大于式(2)計算出的有效掩護距離t。

以上條件可簡稱為2個角度條件和1個距離條件。而直接探尋滿足上述3個條件的雷達對抗無人機任務航線顯然不易，可考慮先尋求滿足一個角度條件的任務航線，再檢查另一個角度條件，最后檢查距離條件。

4 雷達對抗無人機弧形向心航線及有效性分析

如圖4所示，弧形向心航線是指雷達對抗無人機沿特定的圓弧飛行，對敵雷達實施側向干擾，掩護陸軍航空兵突防。

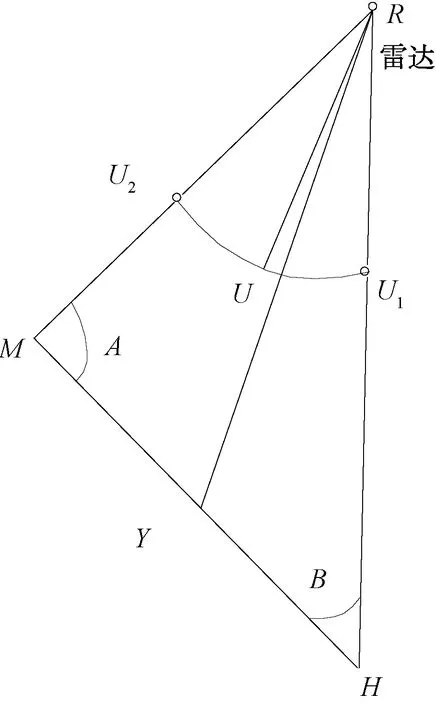
圖4 雷達對抗無人機弧形向心航線示意圖

4.1 弧形向心航線基本含義

弧形向心航線對應的圓心即為圖1中雷達位置，雷達對抗無人機掩護航線對應的弧長，與陸航直升機突防航線的長度成正比，且滿足式(3)：

(3)

式中：和分別為無人機和陸航直升機的飛行速度。

令圖4中∠=，則可知雷達對抗無人機弧形向心航線對應的半徑為：

=

(4)

從圖4中容易看出，當無人機和陸軍直升機同時分別由和點出發沿各自航線飛行后，它們將能夠同時到達和點。持續掩護突防飛行時間為：

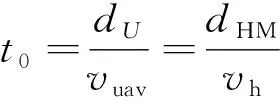
(5)

4.2 弧形向心航線掩護陸航直升機有效性分析

下面從上述的3個條件出發，分析雷達對抗無人機弧形向心航線掩護陸航直升機的有效性。

4.2.1 條件1分析

顯然采用弧形向心航線，由于敵方雷達所在的相對方位始終與雷達對抗無人機飛行方向相垂直，從而采用側向干擾的雷達對抗無人機能夠全程以最大干擾天線輻射方向對準敵雷達，即全程滿足條件1的要求(≤)，不需要進行條件1檢查。

4.2.2 條件2分析

由于雷達對抗無人機和陸航直升機二者分別采用弧形航線和直線航線。因此，上述弧形向心航線僅能保證在掩護航線的起始點和到達點2個時刻，雷達、無人機和直升機保持“三點一線”。其它時刻干擾方向與雷達主瓣方向則存在一定的掩護角度偏差。

假定0時刻無人機和陸航直升機分別由和點出發，則時刻二者分別到達圖4中的與位置，此時無人機相對于航線飛過的角度為：

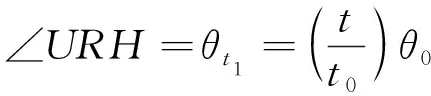
(6)

設和分別為和之間的距離。并令∠=，∠=，則根據Δ，和的值可通過下式求解：

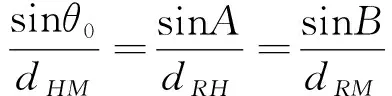
(7)

時刻，直升機飛過的距離為：

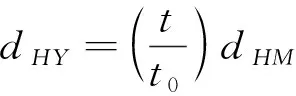
(8)

根據三角形Δ和余弦定理，可求出時刻直升機與雷達的距離：

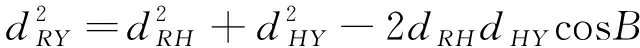
(9)

再根據三角形Δ和正弦定理，可求出時刻直升機相對于航線飛過的角度：

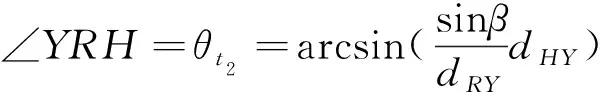
(10)

則時刻，干擾方向與雷達主瓣方向的角度偏差為：

=|-|

(11)

令=max()(0≤≤)，若滿足：

Δ≤052

(12)

則雷達對抗無人機弧線向心航線可滿足條件2要求，從而近似能夠全程保持“三點一線”狀態。

當式(12)條件不滿足時，需要通過改變陸航直升機在威脅區域的進入點的位置，進而改變雷達對抗無人機的弧形向心航線，來探求能夠保持“三點一線”的航線。

4.2.3 條件3分析

容易看出，雷達對抗無人機采用弧形向心航線，各時刻干擾距離始終等于式(6)給出的弧形向心航線所在圓的半徑。代入式(2)可得到有效掩護距離t：

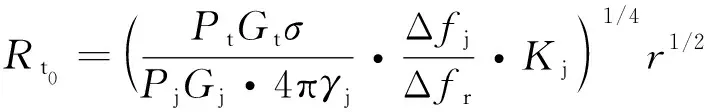
(13)

而時刻，直升機與雷達的距離可由式(9)求出。這樣，只要滿足：

≥t

(14)

則規劃的弧形向心航線也能夠滿足條件3要求。

綜上所述，如果雷達對抗無人機弧形向心航線規劃完畢后，能夠分別滿足式(12)給出的條件2要求、式(13)給出的條件(3)要求，則能夠實時有效地掩護陸航直升機突防到敵方區域內的點。

5 基于側向干擾的雷達對抗無人機弧形向心掩護航線仿真

假設敵方近程防空系統火力范圍為70 km，其制導雷達位于坐標原點(0,0)，制導雷達波束寬度為3°。陸航直升機的速度為300 km/h，雷達對抗無人機的速度150 km/h，陸航直升機進入威脅區域的點為(0，-70)，預定要到達的目標點(-50，-50)。雷達對抗無人機的最大干擾空域輻射范圍2為30°。

其它相關參數假定如下：近程防空系統制導雷達等效輻射功率為500 W，雷達對抗無人機機載干擾機等效輻射功率為900 W，干擾信號對雷達天線的極化損失為0.5，突防陸航直升機的雷達反射截面積為10 m，壓制系數為3.14，機載干擾信號和雷達接收機的頻帶寬度的比值Δ/Δ=2。

5.1 弧形向心航線仿真結果

根據第4節所述和第5節中給出的相關數據，弧形向心航線仿真結果如圖5所示。

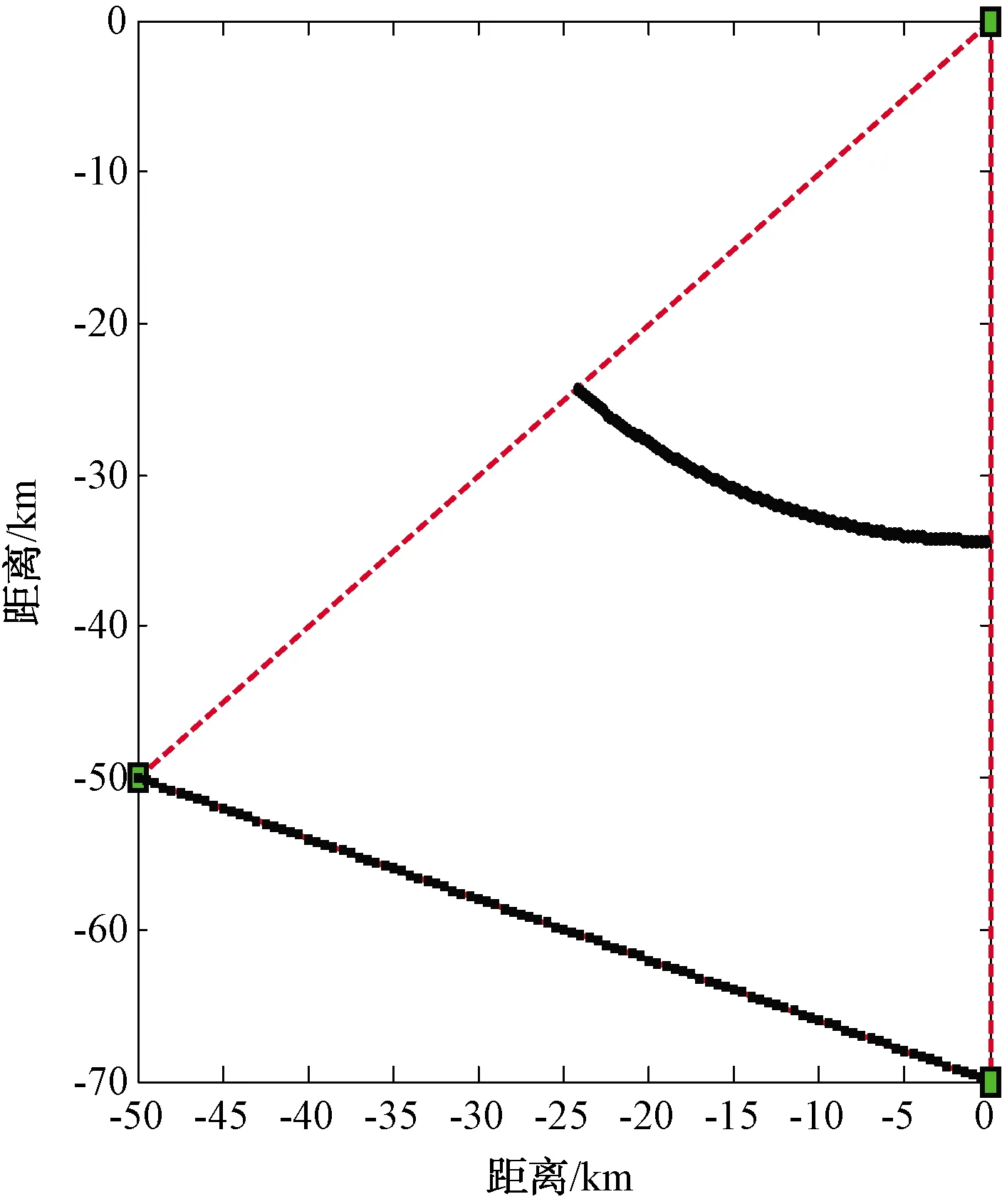
圖5 弧形向心航線仿真結果

仿真計算出的陸航直升機突防航線段總長度為53.8 km，總突防時間為10.8 min。無人機突防弧形向心航線的半徑為35 km。

5.2 條件2檢查

根據式(11)，仿真計算出的各時刻角度偏差Δ結果如圖6所示。

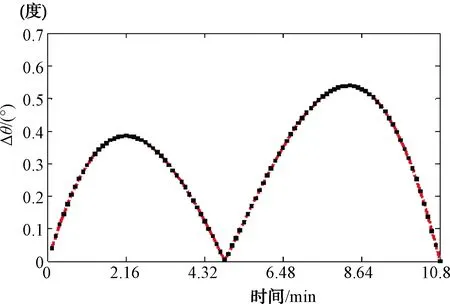
圖6 各時刻Δθt仿真計算結果

圖6中對應的角度偏差最大值Δ=0.52°，小于制導雷達波束寬度的一半(1.5°)，滿足式(12)要求，即上述弧形向心航線能滿足“三點一線”主瓣干擾的條件2要求。

5.3 條件3檢查

根據給定數據和式(13)，可以計算出有效掩護距離t=11.15 km。而根據仿真數據和式(9)計算出的各時刻陸航直升機與雷達距離如圖7所示。

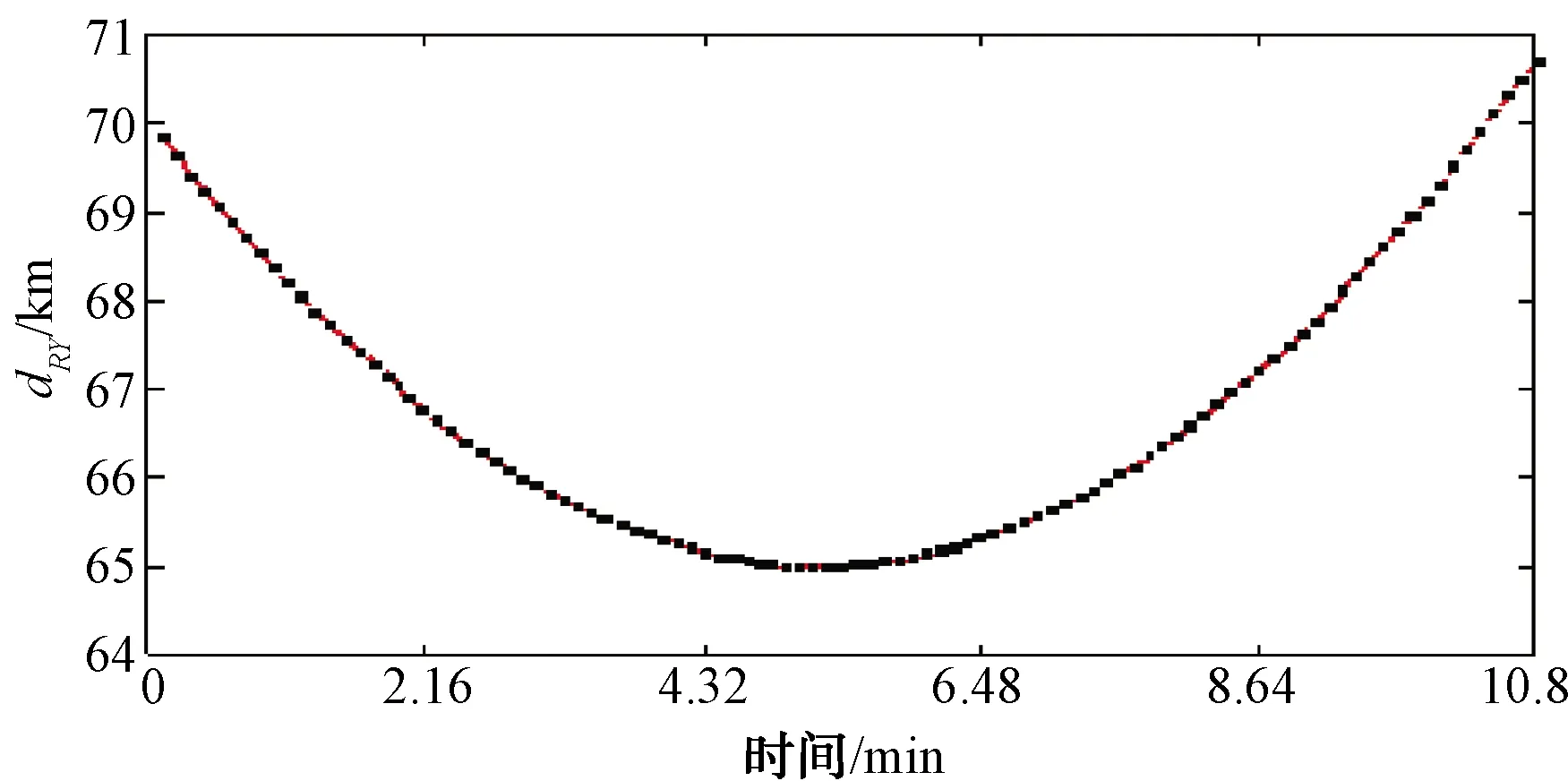
圖7 各時刻陸航直升機與雷達距離仿真計算結果

由圖7可以看出，陸航直升機與雷達距離的最小距離為65.9 km，遠大于計算出的有效掩護距離11.15 km，可滿足條件3要求。

5.4 仿真結論

基于給定仿真條件，雷達對抗無人機采用側向干擾時，規劃出的弧形向心航線能夠有效掩護陸航直升機突防。

6 結束語

論文從雷達對抗無人機側向干擾特點出發，針對掩護陸航直升機突防問題，對弧形向心航線進行了詳細的研究與探討，對雷達對抗無人機作戰運用具有一定的參考價值。