低信噪比條件下雷達對高速運動目標的檢測方法

張 放，徐 磊

(中國船舶集團有限公司第八研究院，江蘇 揚州 225101)

0 引 言

雷達對目標的檢測能力取決于接收機收到的回波信號功率與噪聲或其他干擾功率之比，即信噪比。其中，回波信號功率與目標的雷達反射截面積(RCS)成正比，干擾功率則可能來自于接收機內部噪聲或外界干擾。對于敵方飛機或其他突防武器而言，只要采取降低RCS的技術措施就可以達到降低雷達信噪比的目的，進而使得雷達檢測能力下降。當前，雷達正面臨越來越多隱身飛機和導彈等低RCS目標的威脅，低信噪比條件下的目標檢測成為現代雷達研究的重要技術問題。

在低信噪比條件下，單幀數據很難檢測出目標，因此雷達普遍采用積累提高信噪比，積累時間越長信噪比提高越多。但對于高速運動的目標而言，雷達相干積累時長的增加將使得回波出現跨距離單元移動，導致積累性能下降。為進一步提升檢測能力,需要在積累前進行距離偏移校正。

另一方面，利用圖像處理方法的非相干積累檢測也被用于低信噪比條件下的雷達目標檢測。該方法不作單幀數據處理，而是將幀到幀的歷史數據積累存儲起來，此時目標檢測問題就被轉變為在積累的數據圖像中檢測出目標運動軌跡線條的問題。

1 基于頻域距離偏移校正的檢測

1.1 產生距離偏移的原因

線性調頻脈沖雷達的第個回波的基帶信號可表示為：

(1)

式中：為發射脈寬；為調頻率；為載波頻率；為目標多普勒頻率；為第個脈沖的延遲時間且=2(+)，為目標在0時刻的距離，為目標速度，僅考慮目標勻速運動的情況，即為常數。

經匹配濾波后，信號頻譜表示為：

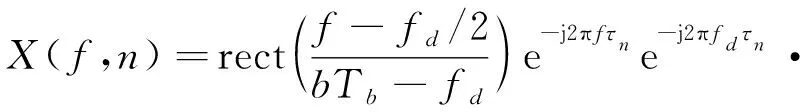
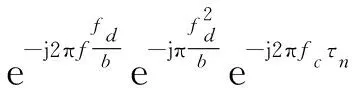
(2)

將式(2)變換到時域，得到輸出：

(,)=(-)sinc[(-)·

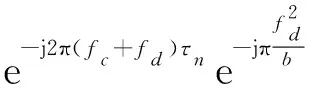
(3)

從式(3)可知，時域信號包絡是一個sinc函數，其信號的峰值位于-。可見，由于每個發射脈沖的延時不同時，脈壓后的信號峰值出現距離偏移，距離偏移現象在目標運動速度越高、雷達相干積累時間越長時的表現得越明顯。此時若對信號進行直接相干積累，目標能量泄漏到其他距離單元，導致相干積累后信號被展寬，信噪比無法提升。

1.2 距離偏移的頻域校正

由式(2)可知，匹配濾波后信號頻譜中的e-j2π相位項，在進行傅里葉反變換后會轉化為時間延遲，且=2(+)。因此，頻域校正的原理是在頻域上分別乘以一個相位補償因子ej2π2，對時間延遲項進行補償。

將式(2)乘以相位補償因子得：

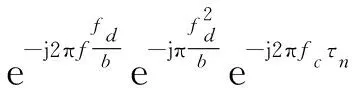
(4)

將式(4)變換到時域，得到輸出：

(,)=(-)sinc[(-)·

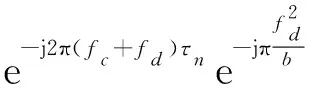
(5)

從式(5)可見，經校正后輸出信號的峰值位于-，距離偏移被校正。

1.3 距離偏移的頻域校正實現算法

在實際情況下，目標(尤其是微弱目標)在檢出之前很難估測出目標的運動速度，因此可以根據實際需要設定目標的最大可能運動速度，然后將等間隔分割成個值，對個速度值的相位補償因子進行搜索。算法流程如圖1所示。

圖1 頻域距離校正算法流程圖

算法流程描述如下：

(1) 預設最大搜索速度，并等分量化搜索步進Δ=/，計算第個脈沖、第個速度值(=1,2,…，(為相干積累脈沖數)；=1,2,…，(為速度量化個數))對應的相位補償因子和匹配濾波器的頻譜并存入存儲器中，然后對接收到的基帶回波進行采樣。

(2) 數字脈壓。將采樣后的基帶數據進行快速傅里葉變換(FFT)后與預先存入的匹配濾波器數據進行相乘，得到脈沖壓縮后的頻域數據。

(3) 頻域校正。假設目標的速度為，將第個脈沖回波壓縮后的頻域數據乘上相應的相位補償因子后進行快速傅里葉逆變換(IFFT)。

(4) 相干積累。對個校正后的脈沖回波進行FFT完成相干積累。

(5) 相干積累結果的檢測。對速度搜索的范圍值對應的相干積累結果進行門限檢測，判定目標的有無。

2 基于Hough變換的檢測

2.1 Hough變換用于雷達目標檢測

在圖像處理中，Hough變換是一種特征檢測方法，常用于形狀的識別和線條的檢測。對于雷達探測而言，將歷史回波數據以距離-時間-回波功率進行存儲，則此數據空間組成的圖像中包含有目標軌跡。如果目標在此期間勻速運動，則目標軌跡表現為一條直線。考慮到實際雷達數據中包含有噪聲，因此對目標的檢測就轉化為在具有噪聲的圖像中檢測直線的問題。利用Hough變換，可將存儲的雷達歷史回波數據空間轉換到參數空間，由于噪聲的隨機性，而目標軌跡點均具有相同的特征點，因此在經過參數空間的積累后，目標軌跡特征點的信噪比提高，再從檢出的特征點恢復出目標軌跡，最終完成目標檢測。

圖2是時間-距離維數據空間圖像上的一條直線，這是一個速度為1 000 m/s的目標30 s的運動軌跡。

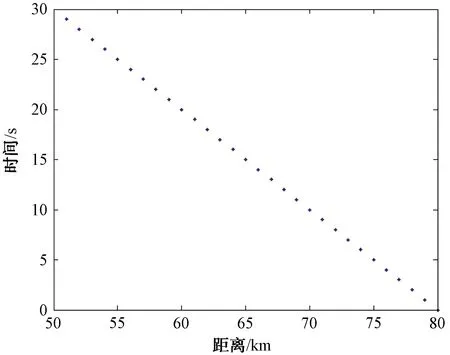
圖2 數據空間平面中的目標直線軌跡

除此直線以外，圖上任意一條直線均可由原點到該直線的垂線距離和垂線與橫軸之間的夾角來確定。將時間-距離維數據空間圖像上的任意一點(用坐標(,)表示)映射到-參數空間的Hough變換表示為：

=cos+sin

(6)

式中:和為數據空間中的取值；為參數空間的自變量，范圍為0°～180°。

對式(5)進行三角變換得到：

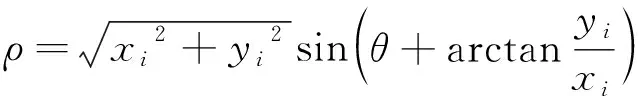
(7)

式(6)表明,經Hough變換后，數據空間中的任意一點對應于參數空間中的一條正弦曲線。而參數空間中的任意一點(,)也能唯一確定數據空間中的一條直線。因此，數據空間中一條直線上的所有點，在Hough變換后的參數空間中就對應為多條正弦曲線的交點。將此特征點提取之后，就可以在數據空間恢復該直線，即檢出目標軌跡。

2.2 基于Hough變換的檢測實現算法

Hough變換的基本原理框圖如圖3所示。

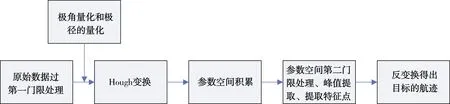
圖3 Hough變換的基本原理框圖

Hough變換的基本步驟如下：

(1) 對原始數據空間的點進行過第一門限處理，將參數空間的極角進行量化，,=1,2,…，。

(2) 對原始數據中超過第一門限的點(,)，針對每個離散的極角，計算=cos+sin。

(3) 確定極徑的量化間隔Δ，對所有計算出的進行量化分區，得到矩陣′。

(4) 對矩陣′通過二值積累或直接積累方式進行積累，得到參數積累矩陣。

(5) 在積累矩陣中進行過第二門限檢測，然后根據基于重心法的方法提取出特征值(,)，通過特征值恢復出目標的航跡。

3 仿真驗證

3.1 頻域距離偏移校正

設線性調頻脈沖雷達載頻3 GHz，脈沖重復頻率600 Hz，發射脈寬40 μs，信號帶寬2 MHz，采樣頻率4 MHz，目標所處初始距離50 km，速度2 000 m/s，積累脈沖數為128。預設搜索最大速度為3 000 m/s，搜索步進15 m/s。

從圖4、圖5、圖6的仿真結果可見，進行頻域距離偏移校正后，相干積累幅度較校正前有較明顯的提升。圖7是相干積累結果與搜索速度的關系圖，在預設目標速度附近可得到最大積累幅度輸出。

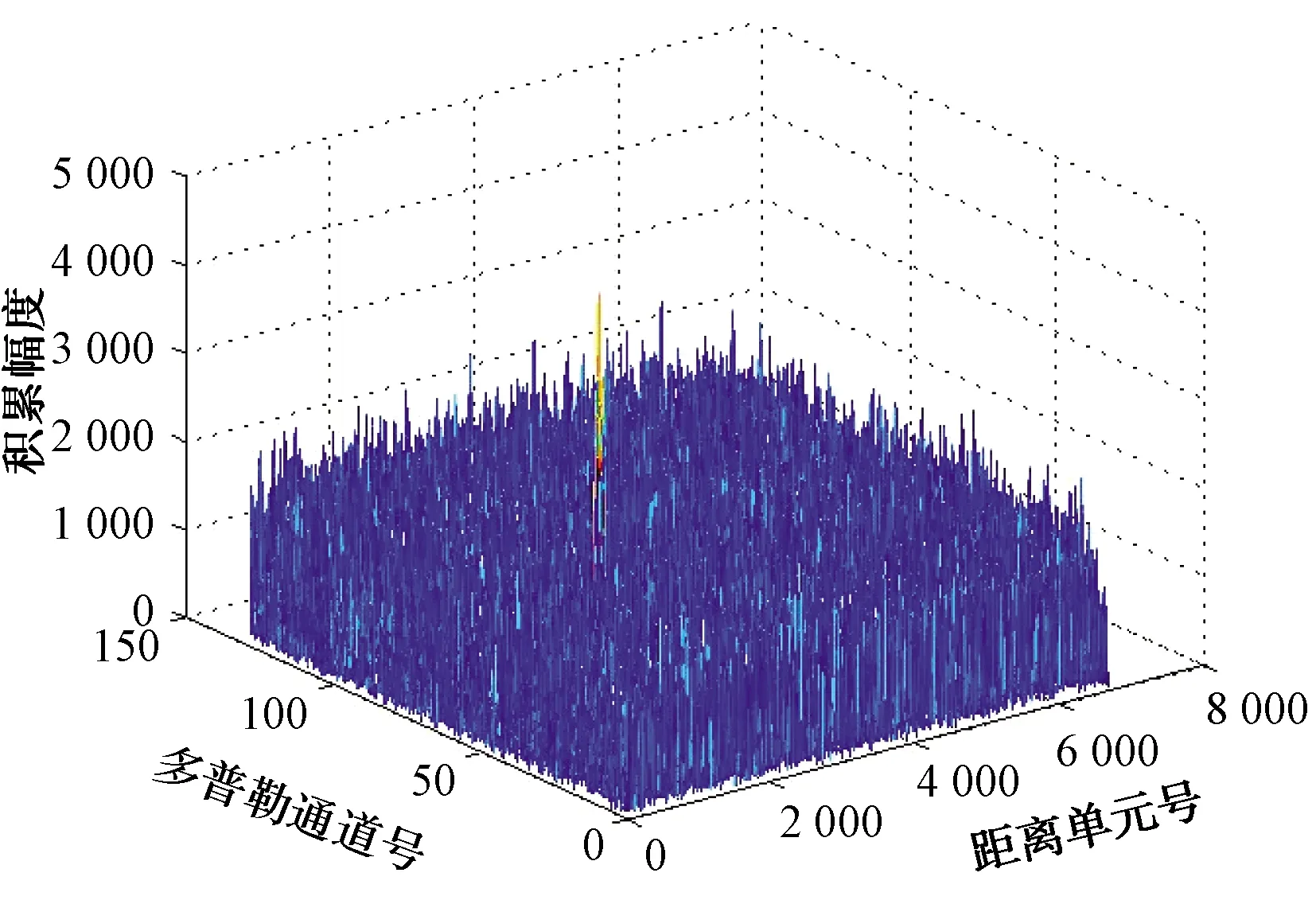
圖4 直接相干積累結果

圖5 校正后的相干積累結果

圖6 校正前后的相干積累結果比較

圖7 相干積累結果與搜索速度的關系

3.2 Hough變換

設0時刻有一目標位于80 km，速度為1 000 m/s，徑向朝雷達運動。

圖8、圖9為構造的目標軌跡的距離-時間-回波強度三維數據空間及疊加高斯白噪聲后的結果。圖10為數據空間過第一門限檢測處理后的結果。

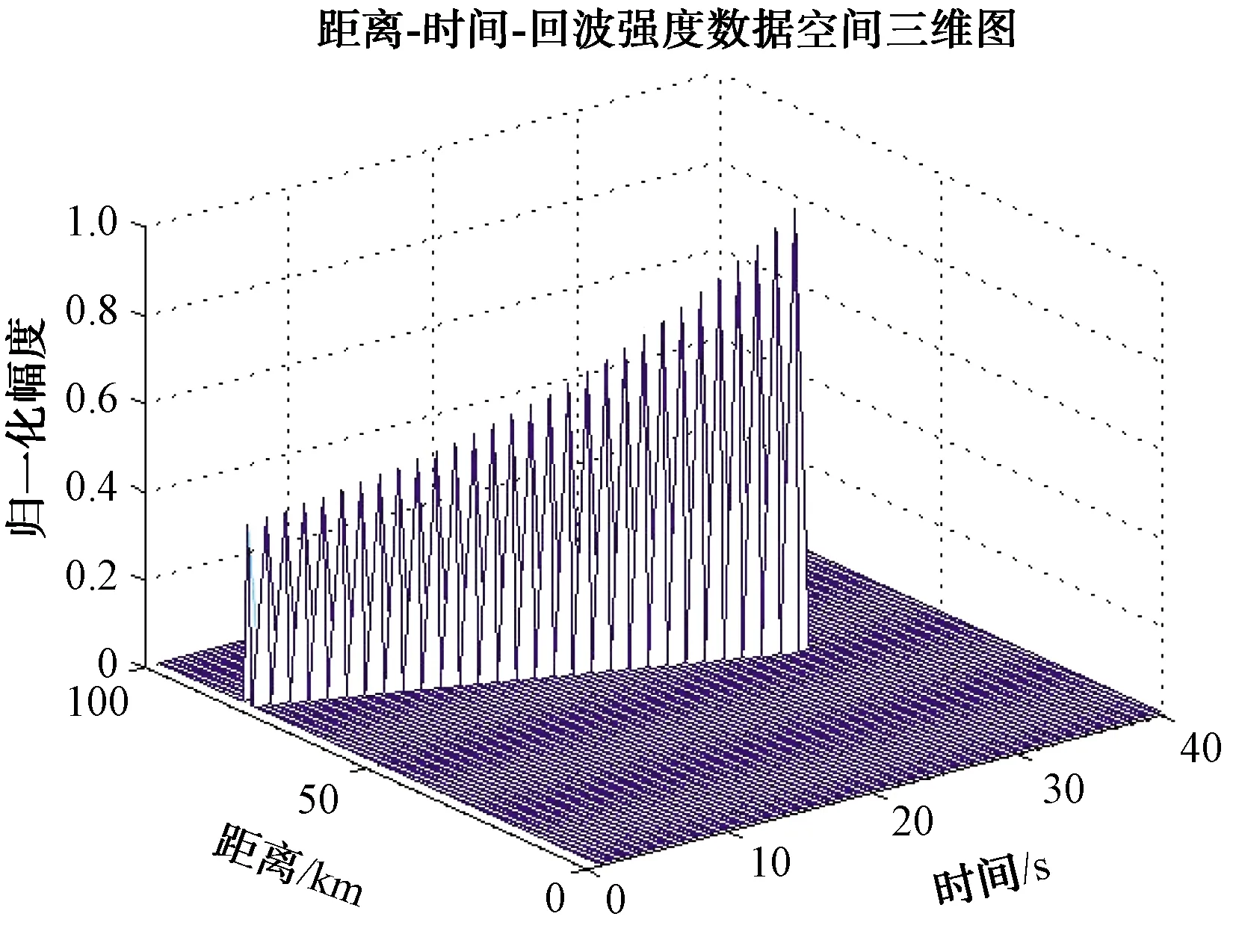
圖8 構造目標軌跡的數據空間三維圖

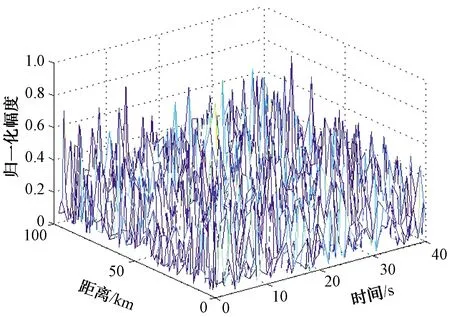
圖9 目標軌跡疊加噪聲后的數據空間三維圖

圖10 數據空間過第一門限檢測后的三維圖

圖11、圖12是將數據空間過第一門限檢測后作Hough變換到參數空間的平面和三維結果視圖。從變換后參數空間的平面圖可見，由于噪聲的干擾，正弦曲線簇無明顯相交于一點的特征點。但從變換后的參數空間三維圖可見，特征點經積累后強度已明顯高于噪聲。從圖13可見，在參數空間進一步作過第二門限檢測后，噪聲干擾被去除，只留下積累后的特征點。

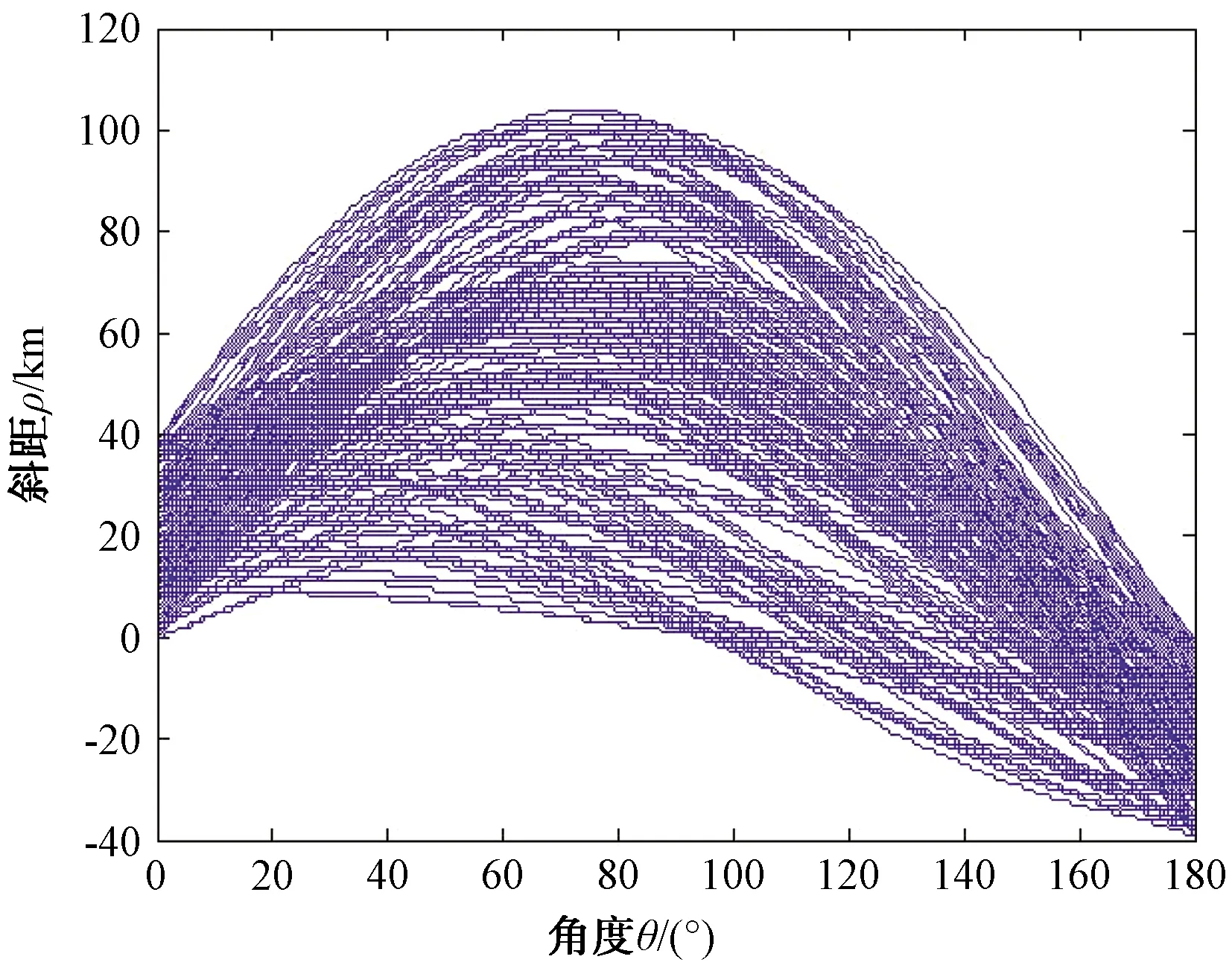
圖11 Hough變換后的ρ-θ參數空間平面圖

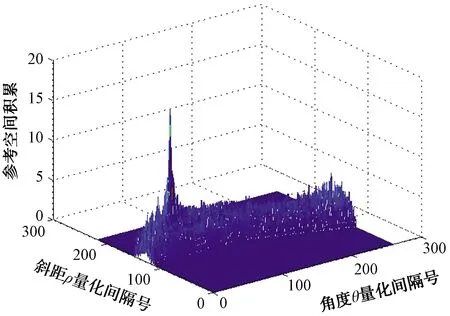
圖12 Hough變換后的參數空間三維圖

圖13 參數空間過第二門限檢測后的三維圖

圖14是將參數空間的特征點提取并恢復目標軌跡，與變換前的目標軌跡作對比，實線和虛線分別是變換前和變換后檢測出的目標軌跡，2條軌跡基本一致，目標被檢出。

圖14 參數空間過第二門限檢測后的三維圖

4 結束語

現代武器技術的發展使得隱身高速目標的威脅日益突出，對雷達探測能力提出了更高要求。本文對基于頻域距離偏移校正的相干積累方法和基于Hough變換的非相干積累方法進行了研究，通過仿真驗證了其在低信噪比條件下目標檢測的有效性。在雷達工程化實踐中，可依照上述處理方法的特點在實際使用中根據需要進行適當應用，以進一步提升復雜條件下雷達的探測能力。