一種異步干擾的自適應檢測和剔除方法

廉志凌

(中國電子科技集團公司第三十八研究所，安徽 合肥 230031)

0 引 言

對于機載雷達來說，由于覆蓋范圍廣，導致它不僅面臨著來自空中的電磁干擾，地面干擾和地面雷達也會對雷達的回波信號帶來調(diào)制，進而影響雷達的性能。特別地，當干擾信號來自于同頻段雷達時，這種干擾稱為同頻異步干擾。

對于異步干擾信號，付啟眾已對其特點進行了分析，指出其有突出性、隨機性和高斯性3個特點，并在此基礎上提出了一種先將接收信號進行動目標指示(MTI)對消，然后采用恒虛警率(CFAR)結合距離雜波圖技術，最后采用門限檢測方法檢測干擾，使用鄰近信號替換干擾信號的處理辦法。

本文在對實測數(shù)據(jù)分析的基礎上，提出了先對回波信號正常處理，然后在頻域根據(jù)頻譜特性判定是否存在異步干擾，若不存在干擾，則處理流程不變；若存在干擾信號，則需要先剔除干擾信號再變換到頻域，并將原來存在干擾信號的頻域數(shù)據(jù)用剔除干擾之后的頻域數(shù)據(jù)替換。與付啟眾的方法相比，本文方法不改變正常的處理流程，實現(xiàn)簡單，運算量小，對平臺是否運動沒有要求。

1 異步干擾的特征

通信設備、廣電設備、導航設備以及地面雷達或者機載雷達均會產(chǎn)生電磁波。當這些設備發(fā)射的頻譜和雷達自身頻譜存在一定的重合時，干擾信號會進入接收機，對接收信號形成調(diào)制。

正常情況下，這些干擾設備或者距離雷達較遠，或者不在同一頻段，或者干擾從雷達的旁瓣進入，從而對于雷達的正常工作基本沒有影響。然而，當干擾從主瓣進入時，干擾信號將會與正常回波信號疊加，從而對信號的幅度和相位產(chǎn)生調(diào)制，在時域表現(xiàn)為幅度的突變(變強或者變?nèi)?和相位的跳變。

圖1為存在異步干擾時采集的實測數(shù)據(jù)，其中圖1(a)、(b)為干擾所在距離單元的幅度特性和相位特性。可以看出無論是信號的幅度還是相位，相對于相鄰脈沖，均發(fā)生了跳變。

圖1(c)、(d)則為存在異步干擾時，一個相干積累時間內(nèi)雷達收到的回波數(shù)據(jù)的特性。其中圖1(c)為回波數(shù)據(jù)的時域特征，圖1(d)為回波數(shù)據(jù)的頻域特征。可以看到，異步干擾信號在時域表現(xiàn)為某些脈沖的部分距離單元的信號幅度異常(增加或減小)，在頻域則表現(xiàn)為頻譜展寬。通常情況下，我們都是在頻域檢測目標的，干擾頻譜的擴展將會使得一些目標很難被檢測到。

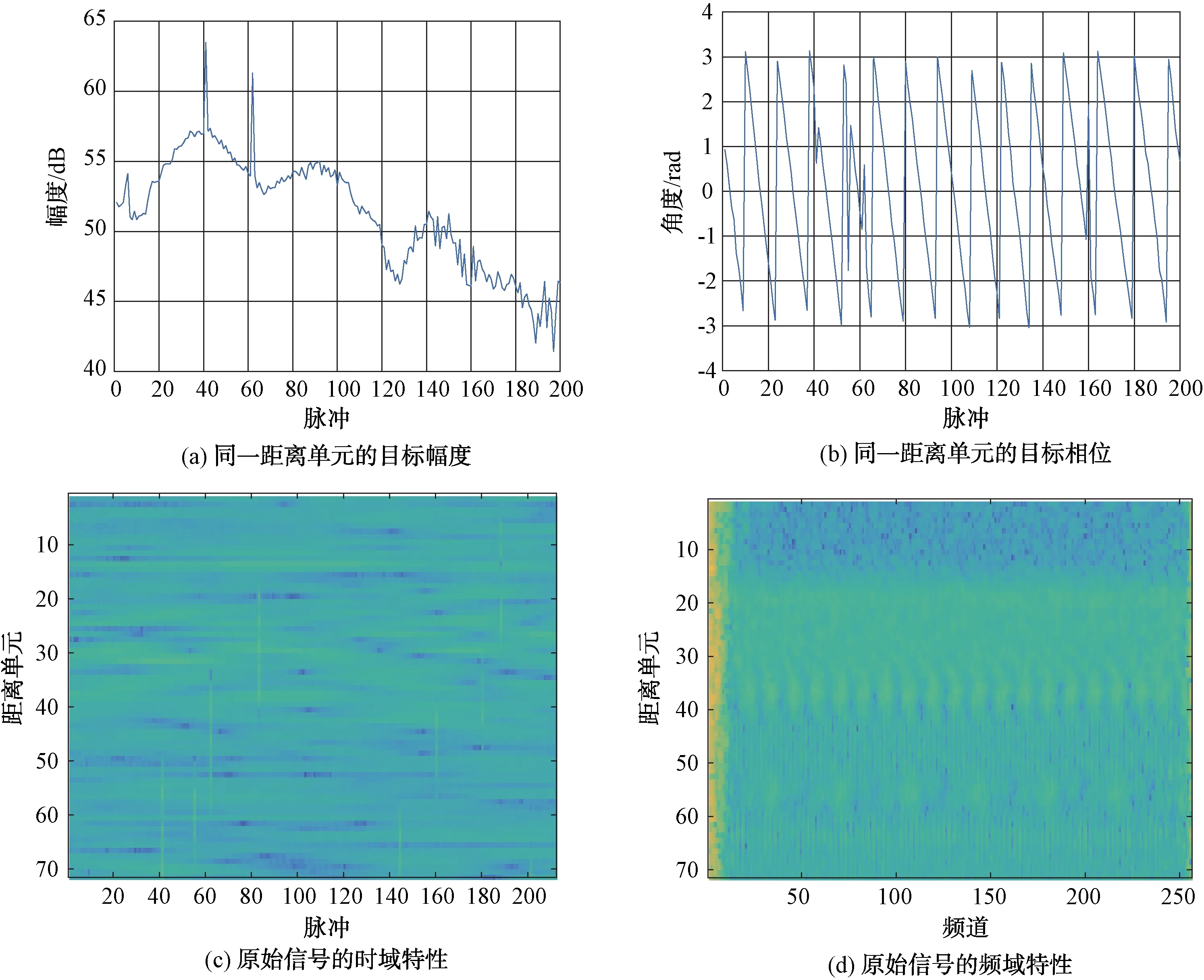
圖1 存在干擾時的信號特征

2 異步干擾的檢測和剔除

顯然，異步干擾的存在會引起雜波譜展寬，可以據(jù)此檢測在頻域回波中是否存在異步干擾。當不存在干擾，或者干擾的影響不大時，依然按照正常處理流程處理；當系統(tǒng)檢測到異步信號時，啟用插值處理，剔除干擾，檢測目標，算法流程如圖2所示。

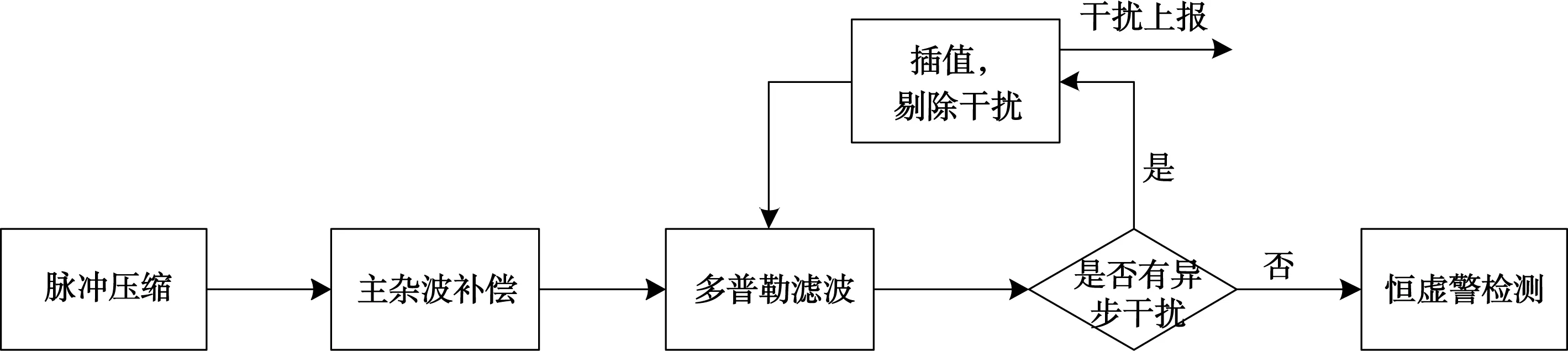
圖2 異步干擾抑制流程

2.1 異步干擾的檢測

異步干擾檢測的原理是，異步干擾的存在會造成雜波譜展寬，抬高系統(tǒng)的噪底。因此，只要檢測系統(tǒng)的噪聲水平，即可確定是否存在異步干擾信號，系統(tǒng)流程圖如圖3所示。算法步驟如下：

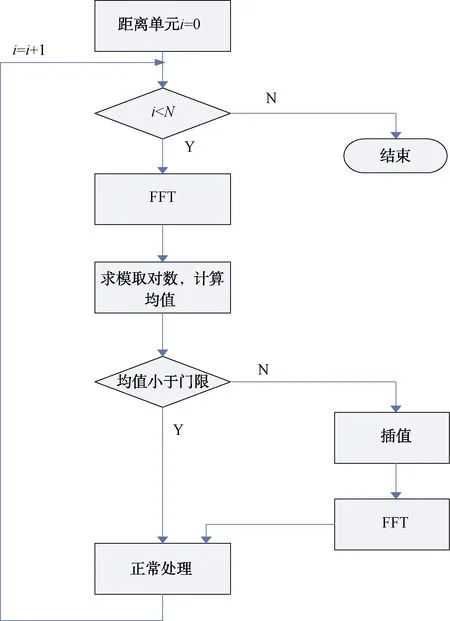
圖3 干擾檢測的流程圖

(1) 首先對分距離單元對雜波補償后的回波信號進行快速傅里葉變換(FFT)，變換到頻域；

(2) 對頻域信號進行求模取對數(shù)；

(3) 對對數(shù)數(shù)據(jù)剔除主雜波之后，求取均值；

(4) 將該均值與檢測門限比較，若大于檢測門限，則說明信號中存在干擾，則需要先插值，然后重新進行FFT變換；

(5) 返回第一步，直至所有距離單元處理完成。

2.2 噪聲背景估計

上述干擾檢測中的門限是由系統(tǒng)的噪聲門限加上手動門限組成的。手動門限的設置不能太高，過高會造成干擾檢測的漏警；也不能設置過低，過低會將正常信號當成干擾信號，增加不必要的運算，甚至造成正常信號的頻譜變差。

而噪聲門限的計算方法與上述方法類似，不同之處在于采用迭代方法估計系統(tǒng)噪聲，方法步驟如下：

(1) 首先對分距離單元對雜波補償后的回波信號進行FFT，變換到頻域；

(2) 對頻域信號進行求模取對數(shù)；

(3) 對對數(shù)數(shù)據(jù)剔除主雜波之后，求取均值；

(4) 對整個回波信號每個距離單元的均值求和，然后求取二次均值。

噪聲背景更新的公式為：

(1)

式中：為更新后的噪聲門限；-1為更新前的噪聲門限；為當前波位的噪聲均值；為需要滑窗的波位個數(shù)。

2.3 插值處理

雷達在某個脈沖接收到的回波信號可表示如下：

=·exp(j2π(-1)+j2π)+

(2)

式中：為系統(tǒng)的幅度響應；為多普勒頻移；為線性調(diào)頻信號的調(diào)頻率；為距離上的快時間；為方位向的慢時間；為系統(tǒng)噪聲；為脈沖號。

假定某個距離單元的第個脈沖存在異步干擾，則第-1、、+1脈沖的信號可分別表示如下：

-1=-1·exp(j2π(-1)+j2π)+-1

(3)

=·exp(j2π+j2π)++

(4)

+1=+1·exp(j2π(+1)+j2π)++1

(5)

一般來說，信號或者雜波的強度遠大于噪聲的強度，在這里可以將其忽略，則上述信號可分別表示如下：

-1=-1exp(j-1)=-1·exp(-j2π)·

exp(j2π+j2π)

(6)

=exp(j)=·

exp(j2π+j2π)+

(7)

+1=+1exp(j+1)=+1·

exp(j2π)·exp(j2π+j2π)

(8)

顯然，如果沒有干擾信號的話，-1，和+1近似滿足線性相位關系，同時，在這么短的時間內(nèi)，幅度-1、、+1也可以認為近似滿足線性關系，這是通過插值估算的理論依據(jù)。

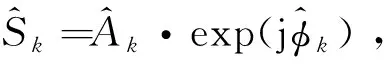
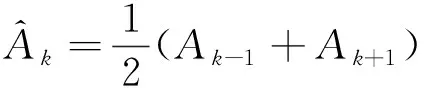
(9)

(10)

2.4 實測數(shù)據(jù)的處理

將本文方法應用于上述實測數(shù)據(jù)，處理結果如圖4所示。從圖4可以看出，信號的幅度和相位更加平滑，脈間跳變基本消失，反映到頻譜上，就是雜波區(qū)和噪聲區(qū)更加明顯，提高了目標的檢測能力。

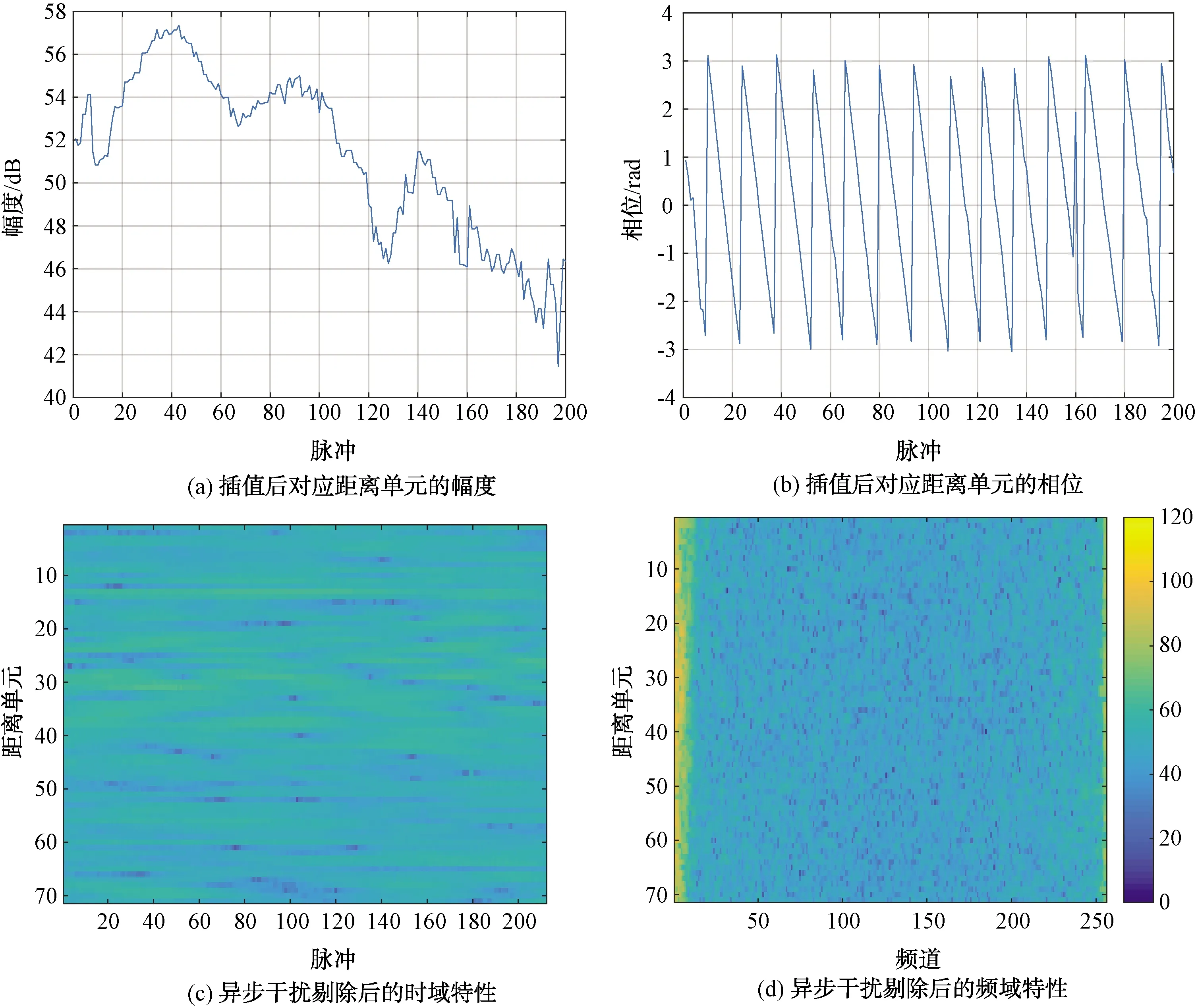
圖4 干擾抑制之后的信號

3 結束語

本文提出了一種在頻域自適應檢測異步干擾，并進行干擾剔除的方法。由于在系統(tǒng)不存在干擾的波位或者距離單元，不需要插值運算，可大大降低系統(tǒng)運算量。同時，由于本文所提方法基本不依賴于雷達的應用場景，可應用于包括但不限于機載雷達的異步干擾抑制，而實測數(shù)據(jù)的處理結果則驗證了本文所提方法的有效性。