離散函數與排列組合之關聯探究

天水師范學院數學與統計學院 (741001) 唐保祥

1 問題提出

函數是高中數學的核心和靈魂,是必修課程的五個主題之一(預備知識、函數、幾何與代數、概率與統計、數學建模活動與數學探究) ,是貫穿高中數學課程的四條主線之一(函數、代數幾何、概率與統計、數學建模活動與數學探究)[1].在2019年人教A版普通高中數學教材中,函數安排必修第一冊中集中學習,在之后的各冊教材中,涉及函數問題多數是連續函數的應用.函數有連續變量函數與離散變量函數(定義域是有限集或可列集合的函數稱為離散變量函數,以下簡稱離散函數)之分.離散函數,在2019年人教A版高中數學課本選擇性必修第二冊概率與統計、選擇性必修第三冊數列中學習.離散函數與排列組合內容有密切的關系[2-7].中學數學對離散函數作一些深入探究,不僅會促使學生深化函數概念的理解,而且還能引導和啟發學生從不同角度、不同層次對函數概念進行深入探究,能夠挖掘鞏固教材各章節知識點之間的內在聯系,發展學生的數學抽象能力,使學生的數學素養得到提升.

鑒于上述原因,本文通過數例,探究離散函數與排列組合內容之間的關聯,以期有拋磚引玉之效.

2 問題呈現

例1 已知數集A={a1,a2,…,am},B={b1,b2,…,bn},求數集A到數集B的所有不同函數的個數.

解：對任意一個函數f:A→B,?ai∈A,f(ai)∈B,i=1,2,…,m,每個f(ai)在數集B中選擇象的方法都有n(i=1,2,…,m)種,因為不同的象對應不同的函數,所以數集A到數集B的不同函數共有nm個.

例2 已知數集N={1,2,…,n},如果函數f:N→N滿足?i,j∈N,當i≤j時,f(i)≤f(j),本文稱該函數f是離散單調遞增函數;如果函數f滿足?i,j∈N,當i≤j時,f(i)≥f(j),則本文稱該函數f是離散單調遞減增函數;如果存在i∈N,f(i)=i,則本文稱離散函數f是含有不動點的離散函數,并稱i是離散函數f的一個不動點.

(1)求N到N的所有不同的離散單調遞增函數的個數;

(2)求N到N的所有不同的離散單遞減函數的個數;

(3)求N到N的所有不同的既非離散單調遞增又非離散單調遞減函數的個數;

(4)求N到N的所有不同的恰好含有i個不動點的離散函數的個數;

(5)求N到N的至少含有一個不動點的離散函數的個數.

解：(1)通過具體實例,探究單調函數數目的規律.由例1可知,當N={1,2,3}時,N到N的所有不同的函數共有33=27個.27個不同函數如表1所示:

表1

根據題目中離散單調遞增函數的定義,由表1看出,函數f:{1,2,3}→{1,2,3}中共有10個離散單調遞增函數,它們分別是f1,f2,f3,f5,f6,f9,f14,f15,f18,f27.離散函數對應的點(i,fk(i))(i=1,2,3)是橫縱坐標都是1至3的整數,本文稱之為格點.在坐標平面,把離散函數對應的格點與點(1,1)、(4,3)用水平或豎直的線段連接起來,畫出f1,f2,f3,f5,f6,f9,f14,f15,f18,f27的圖象如圖1所示:

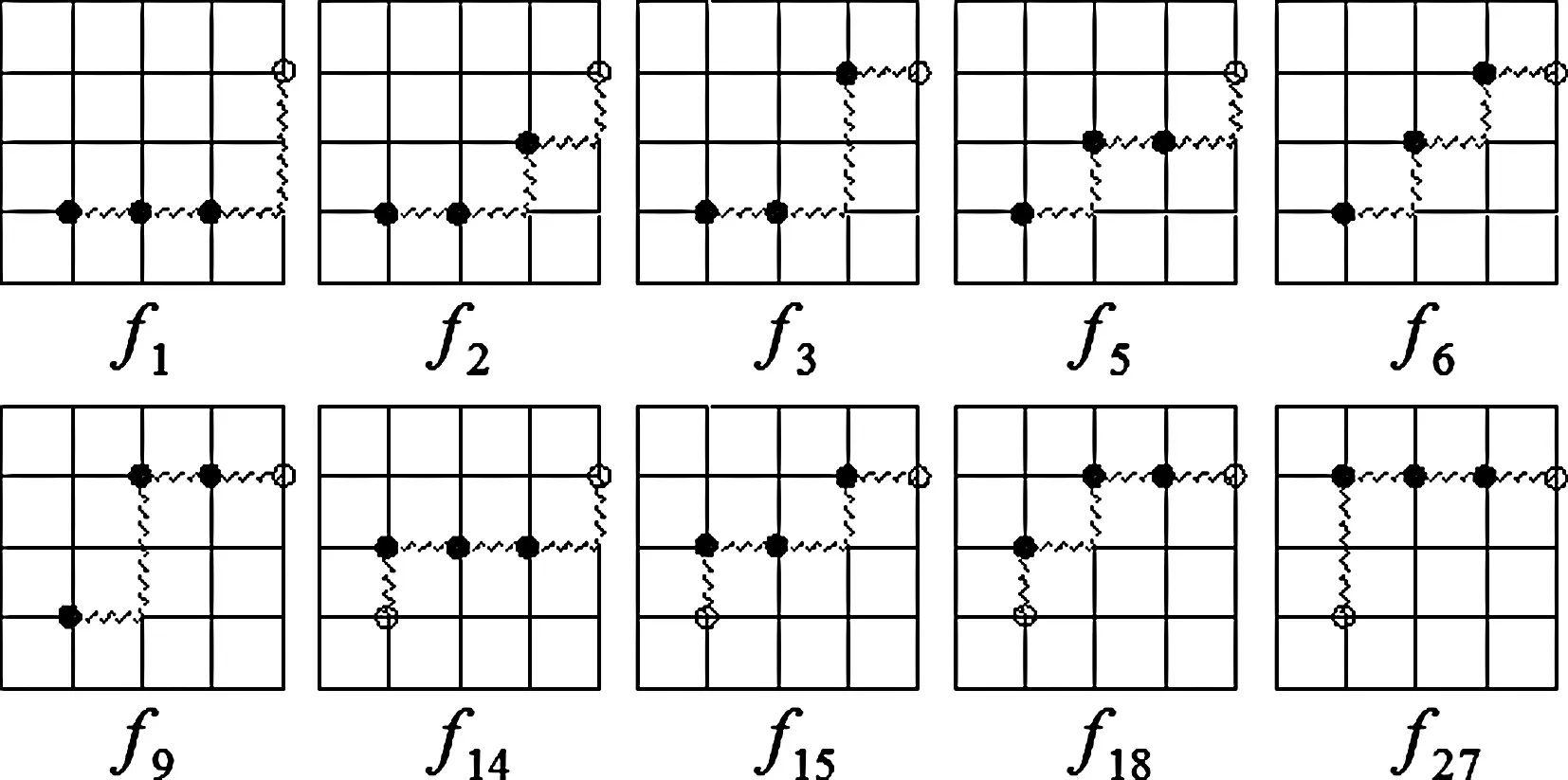
圖1

由圖1可知,每一個離散單調遞增函數對應著沿小正方形的邊,由點(1,1)到點(4,3)一條“最短路徑”;反過來,每一條沿小正方形的邊由點(1,1)到點(4,3)“最短路徑”對應著一個離散單調增函數f:{1,2,3}→{1,2,3}.

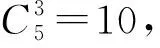
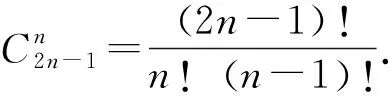
(2)由表1看出,離散函數f:{1,2,3}→{1,2,3}中共有10個離散單調遞減函數,它們分別是f1,f10,f13,f14,f19,f22,f23,f25,f26,f27.在坐標平面,把離散函數對應的格點與點(0,3)、(3,1)用水平或豎直的線段連接起來,畫出f1,f10,f13,f14,f19,f22,f23,f25,f26,f27的圖象如圖2所示:

圖2

由圖2可知,每一個離散單調遞減函數f:{1,2,3}→{1,2,3}對應著沿小正方形的邊,由點(0,3)到點(3,1)一條“最短路徑”;反過來,每一條沿小正方形的邊由點(0,3)到點(3,1)“最短路徑”對應著一個離散單調遞減函數f:{1,2,3}→{1,2,3}.

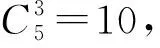
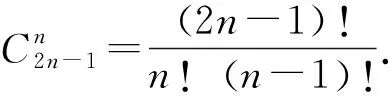
(3)當N={1,2,…,n}時,既是離散單調增的函數又是離散單調遞減的函數有n個,它們是fj(i)=i,i=1,2,…,n;j=1,2,…,n.

所以N到N的既非離散單調增又非離散單調遞減函數的數目為

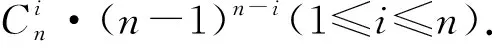
(5)設f是N到N的任意一個不含不動點的離散函數,則?i∈N,f(i)≠i,所以f(i)只能取{1,2,…,i-1,i+1,…,n}中任意一個值,i=1,2,…,n.所以N到N的不含不動點的離散函數共有(n-1)n個.于是,N到N的至少含有一個不動點的離散函數的個數為nn-(n-1)n.

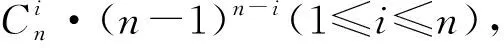
例3 已知數集A={a1,a2,…,am},B={b1,b2,…,bn},若m≤n,求滿足條件?ai,aj∈A,當ai≠aj時,f(ai)≠f(aj)的所有不同函數f:A→B的個數.

例4 已知A={1,2},B={0,3,4},給出數集A到數集B的值域中恰有兩個元素的所有函數f:A→B.

解：集合B={0,3,4}的兩個元素的子集有三個,它們分別是:B1={0,3},B2={0,4},B3={3,4}.所以值域中恰有兩個元素的函數f:A→B1有2個、函數f:A→B2有2個、函數f:A→B3有2個.所以值域中恰有兩個元素的所有函數f:A→B共有6個,這6個不同函數如表2所示:

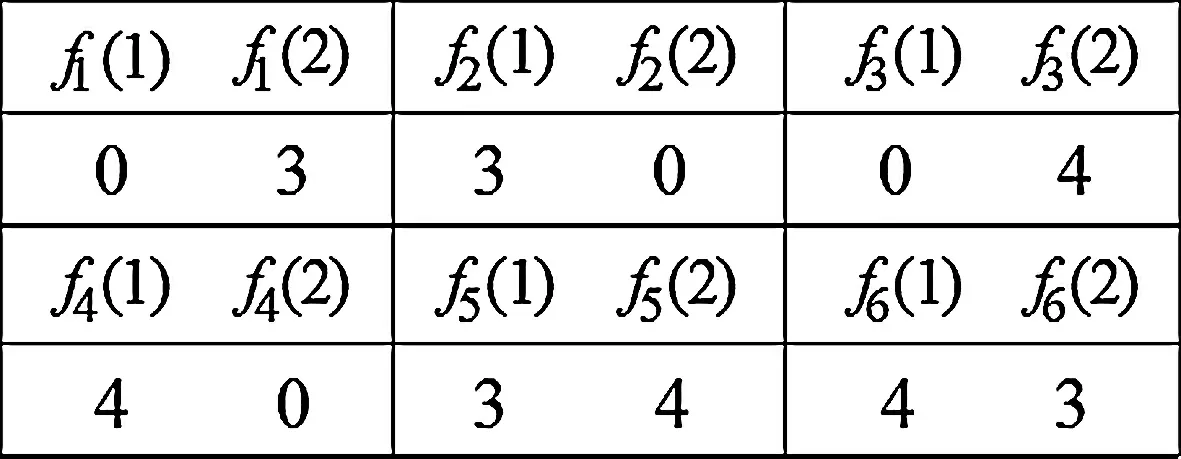
表2

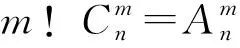
例5 已知A={1,2,3,4},B={0,1,2},函數f:A→B,滿足f(1)+f(2)+f(3)+f(4)=4,求滿足條件的函數共有多少個？

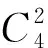
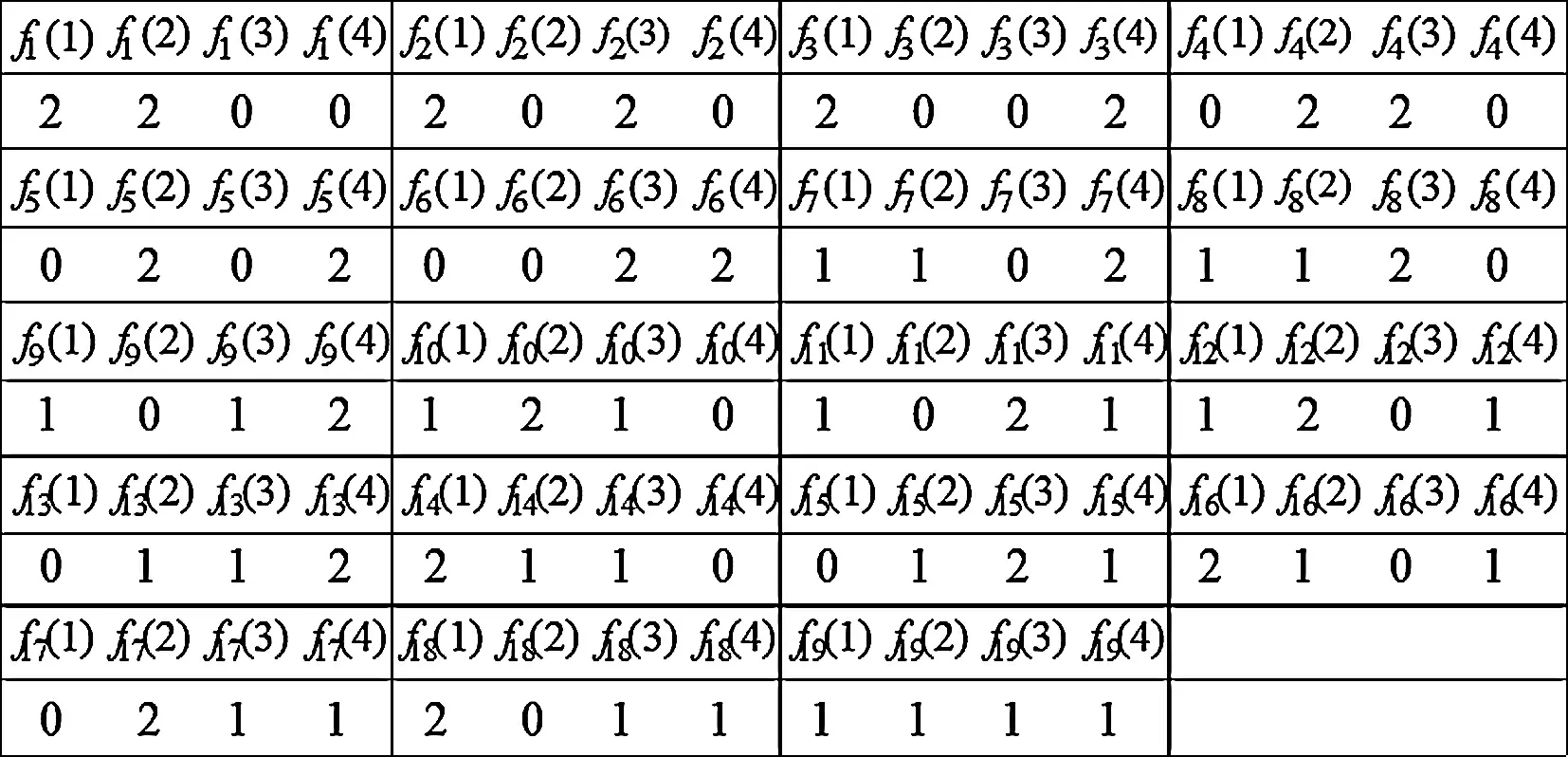
表3