基于鏡像原理對(duì)導(dǎo)電平面半空間并矢格林函數(shù)的研究

海 波，雒向東

（1.蘭州城市學(xué)院 信息工程學(xué)院，甘肅蘭州 730070；2.甘肅高師學(xué)報(bào)編輯部，甘肅蘭州730070）

在求解電磁場各類邊值問題時(shí)，并矢格林函數(shù)方法是一種有效的方法.利用該方法解決電磁場邊值問題關(guān)鍵是要獲得具體的并矢格林函數(shù)關(guān)系，在研究復(fù)雜多面導(dǎo)體邊界電磁場邊值問題時(shí)，獲得導(dǎo)電平面半空間并矢格林函數(shù)關(guān)系是非常重要的，它對(duì)于解決此類問題具有重要應(yīng)用價(jià)值.但導(dǎo)電平面半空間并矢格林函數(shù)關(guān)系詳細(xì)推證文獻(xiàn)較少，該文基于鏡像法原理，利用自由空間并矢格林函數(shù)關(guān)系，詳細(xì)推證導(dǎo)電平面半空間并矢格林函數(shù)關(guān)系，獲得了該表達(dá)式的完整形式，其研究結(jié)果可為導(dǎo)電劈等電磁場邊值問題的解決提供方便.

1 鏡像原理

鏡像法是依據(jù)唯一性定理求解具有理想導(dǎo)體邊界電磁場邊值問題的一種方法.其基本原理就是用原有源的鏡像來代替理想導(dǎo)體邊界對(duì)場的影響，因?yàn)槔硐雽?dǎo)體邊界上電場強(qiáng)度切向分量等于零，所以原有源與虛擬鏡像源應(yīng)當(dāng)保證在原來理想導(dǎo)體邊界上電場強(qiáng)度的切向分量等于零.圖1 畫出了與理想導(dǎo)體邊界平行或垂直放置的電流源和磁流源的鏡像元.根據(jù)鏡像法原理，與理想導(dǎo)體平面邊界平行放置的電流源，其鏡像元方向與其相反；與理想導(dǎo)體平面邊界垂直放置的電流源，其鏡像元方向與其相同.對(duì)于磁流元，其鏡像正好與電流源的情況相反[1].

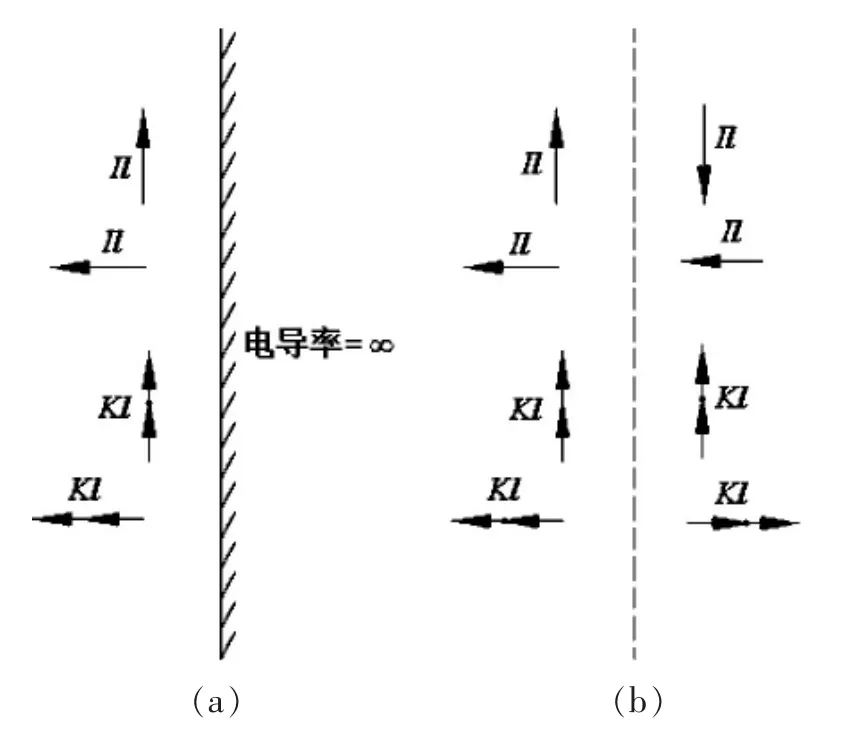
圖1 電流源和磁流源鏡像示意圖

2 自由空間并矢格林函數(shù)

電型和磁型并矢格林函數(shù)滿足（1）（2）式[2]，

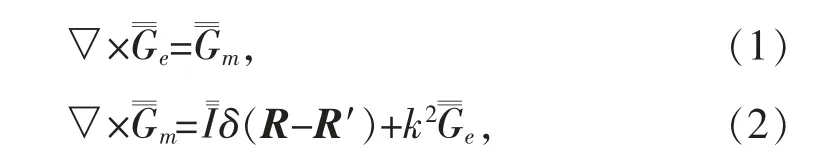
對(duì)（1）式兩邊取旋度代入（2）式得

對(duì)（2）式兩邊取旋度代入（1）式得

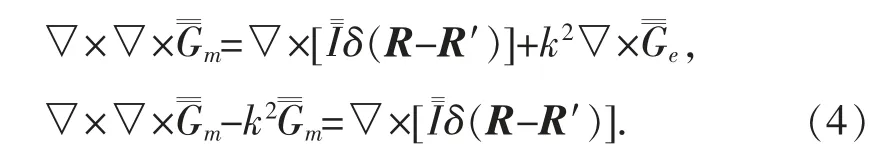
式（3）和（4）為并矢形式的波動(dòng)方程.求解這兩個(gè)方程有好幾種方法，下面就借助位函數(shù)這種方法求解[3].

依據(jù)時(shí)諧場位函數(shù)理論[4]，對(duì)有源區(qū)域非齊次矢量波動(dòng)方程

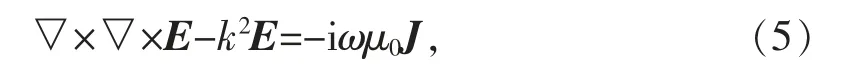
從源出射波的矢勢(shì)表達(dá)式為

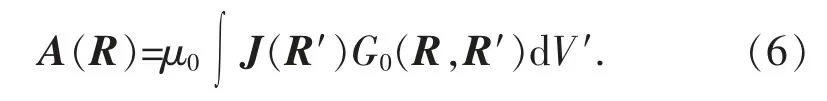
若采用關(guān)系

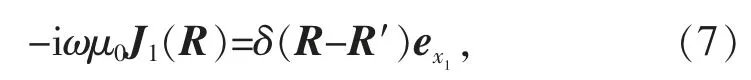
表示ex1指向的無窮小電偶極子的電流分布，則可得

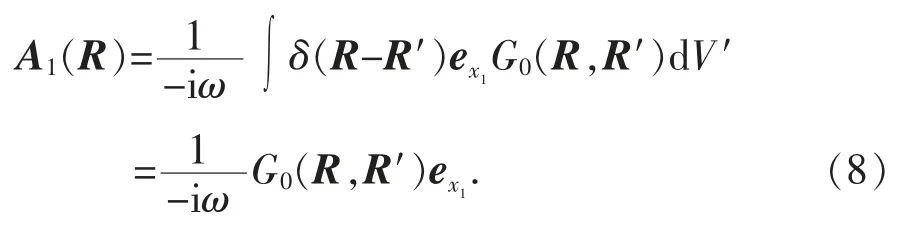
由位函數(shù)表示的電場公式[4]

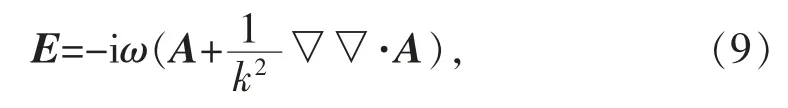
將（8）式代入（9）式得

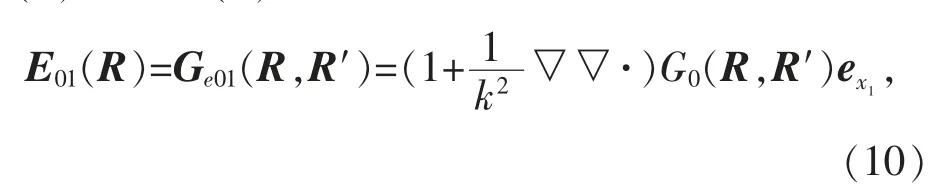
這里Ge01（R，R′）表示指向的源在自由空間的電型矢量格林函數(shù).同樣，對(duì)于指向的源和指向的源分別得到

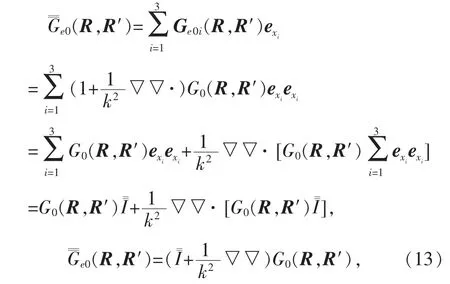
式（13）中

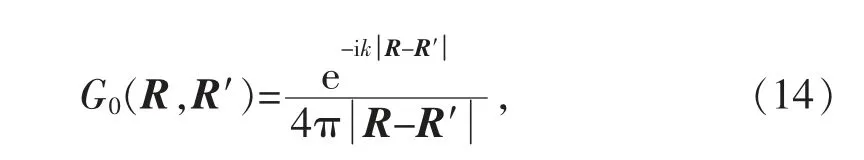
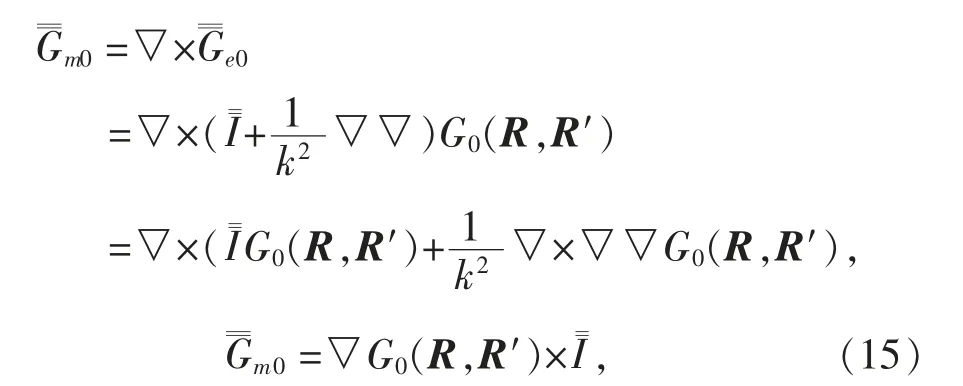
G0（R，R′）為三維標(biāo)量波動(dòng)方程的自由空間標(biāo)量格林函數(shù)[5].

3 半空間并矢格林函數(shù)

將上半空間內(nèi)原并矢電流源的自由空間電型并矢格林函數(shù)和原電流源在下半空間的鏡像所產(chǎn)生的自由空間電型并矢格林函數(shù)相疊加，就可求得導(dǎo)電平面半空間的第一類電型并矢格林函數(shù)，圖2（a）和（b）表示原問題和它的等效問題.

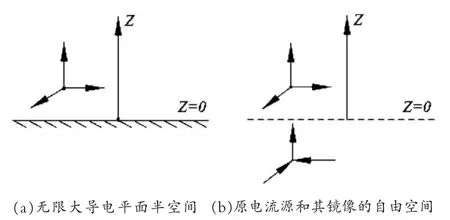
圖2 原問題和等效問題示意圖

圖2（a）表示的上半空間內(nèi)并矢電流源產(chǎn)生的自由空間，電型并矢格林函數(shù)由式（13）給出，其中

原電流源在下半空間的鏡像并矢源在位置矢量為R 點(diǎn)產(chǎn)生的自由空間并矢格林函數(shù)為

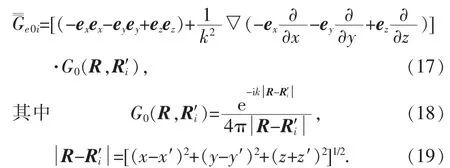
于是導(dǎo)電平面半空間并矢格林函數(shù)為

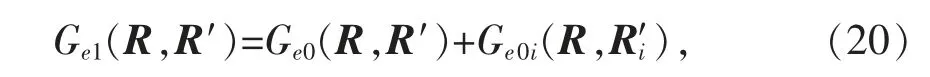
（17）式也可改寫為

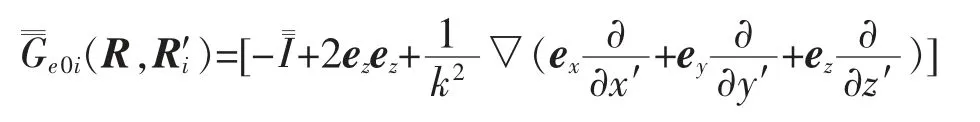
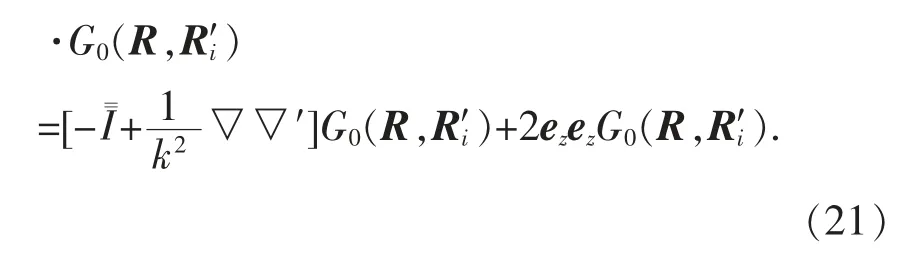
（13）式也可寫為

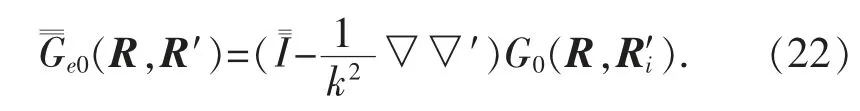
因此導(dǎo)電平面半空間并矢格林函數(shù)為

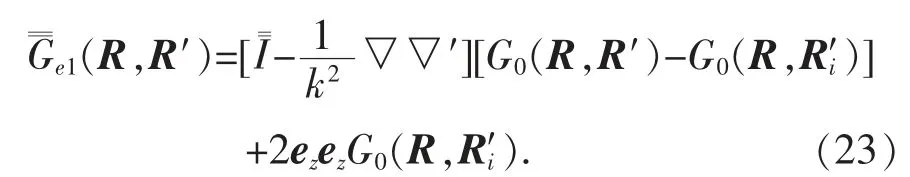
可以證明在位于z=0 的導(dǎo)電平面上

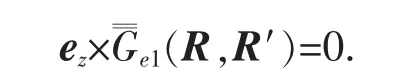
若引入輔助單位并矢

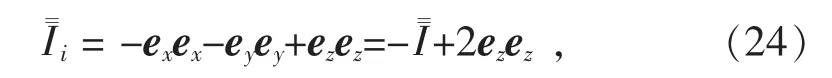
將式（23）帶入（25）式

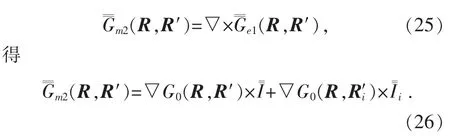
這就是第二類磁型并矢格林函數(shù)的表達(dá)式.

4 結(jié)束語

文中利用鏡像法研究了導(dǎo)電平面半空間并矢格林函數(shù)[6-7]，利用此方法還可以推廣到導(dǎo)電劈等情況，只要劈角π/n 的n 是一整數(shù).當(dāng)n=1 時(shí)，它就是上面討論的平面導(dǎo)體面的情況[8].當(dāng)n 是大于1 的整數(shù)時(shí)，鏡像的個(gè)數(shù)是有限的，此類邊值問題的第一類電型并矢格林函數(shù)理論上可以用同樣的方法得到，具體研究文獻(xiàn)較少，因此還可做進(jìn)一步的研究.