依托數形結合 助推圖形測量

[摘? 要] “圖形的測量”是積累幾何活動經驗、培養空間思維的主要載體。在“圖形的測量”板塊教學時，通過結合實例、動手操作、溝通聯系，以形助數讓圖形度量更直觀;通過對比、梳理、反思，以數釋形讓圖形計算走向深刻;通過以形表思、以數輔形、數形互通，把復雜問題簡單化，抽象問題直觀化，使知識的學習更加深刻明了。

[關鍵詞] 數形結合;圖形度量;圖形計算;問題解決

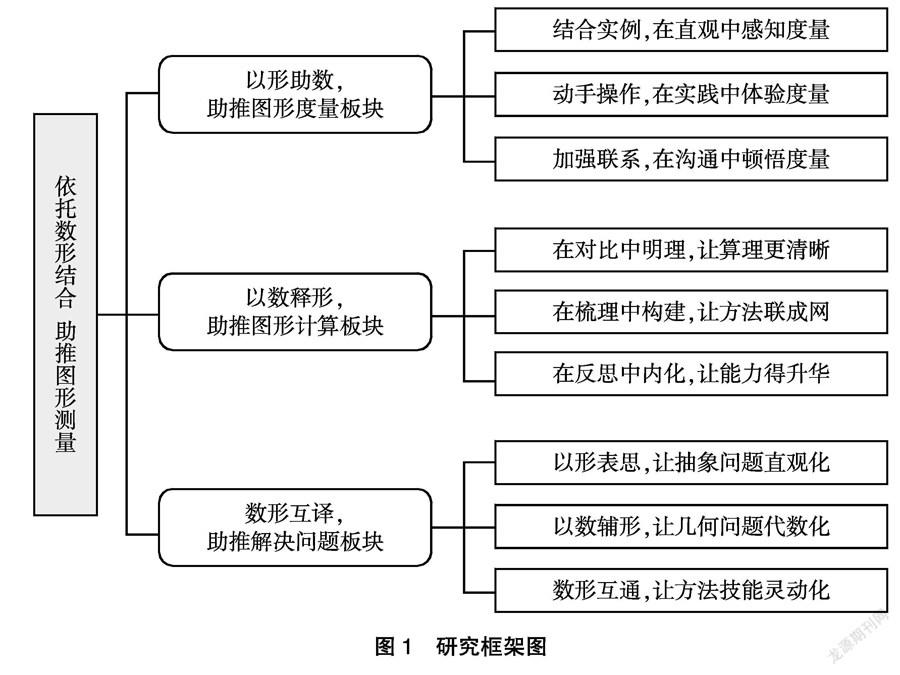
數形結合思想是新課程標準體現的一項重要的數學思想，對培養學生的數學素養至關重要。“圖形的測量”是小學數學教材中積累幾何活動經驗、培養空間觀念的主要載體。著名數學家華羅庚曾說過：“數缺形時少直觀，形少數時難入微;數形結合百般好，隔離分家萬事休。”在“圖形的測量”的教學過程中，挖掘其中蘊含的數形結合思想方法的內容（圖1），能貫通學生心中數與形的內在聯系，幫助學生積累數學基本活動經驗，還能引導學生建立空間觀念，培養空間思維，提高問題解決能力。

一、以形助數，助推圖形度量板塊

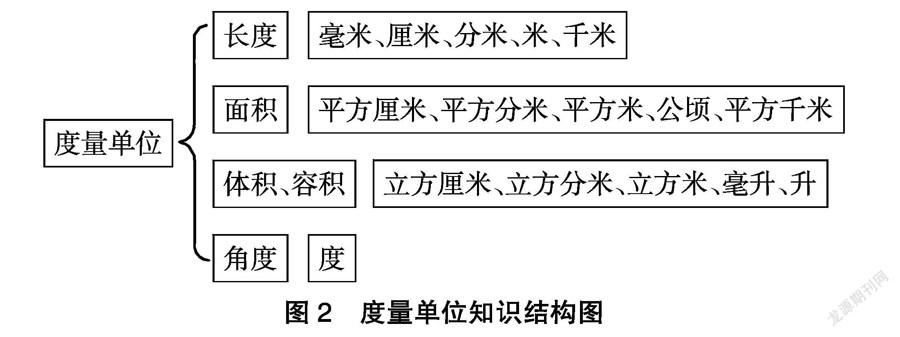
加強對度量單位實際意義的理解，對“圖形的測量”板塊的教學起到決定性的作用。教學時，教師應讓學生明白為什么要統一度量單位，經歷度量單位產生的過程，以及度量單位間的區別與聯系。要想準確區分這些度量單位并正確運用，教師應嘗試以形助數，讓“度量單位”變直觀，構建完整的度量單位的知識網，以便知識的靈活應用（圖2）。

（一）結合實例，在直觀中感知度量

度量板塊教學時，教師要著眼于度量表象的建立。讓學生親密接觸度量的對象，引導學生對具體實例進行觀察、比較等感知活動，給學生豐富感知的機會。

例如“面積的認識”，身邊哪些物體有面？讓每個學生都找一找，會發現面無處不在，桌子、凳子、練習本、文具盒等，這些物體都有面，面是長在物體上的，這些物體如果畫下來就是一個平面圖形。再看一看、摸一摸這些面，會知道面是看得見、觸摸得到的。再比一比，會發現這些面有大有小，面的大小就是它們的面積。如此，學生對面的大小有了直觀的感知。

“面積”的學習，標志著學生的認知領域從一維空間延伸到二維區域，這是學生認知系統一個質的飛躍。通過摸一摸，直觀感知面是立體圖形的一部分，有曲面和平面之分;再通過比一比，認識到面是有大小的。結合具體實例，理解面積的含義，對面積的進一步學習有很好的促進作用。

（二）動手操作，在實踐中體驗度量

度量知識的即時掌握并不重要，重要的是在獲取知識的過程中學生活動經驗的積累。度量知識的真正掌握需要教師給學生提供動手操作的機會，讓學生經歷用不同的方式進行測量、感受、理解的過程。讓學生在操作中體驗，在體驗中掌握。在反復操作中體驗度量單位，加深對度量單位的理解，建立度量單位的概念，讓度量知識真正內化。

例如“面積單位的認識”的教學，讓學生找一找，找身邊的1平方厘米、1平方分米、1平方米的平面;比一比，用學具驗證自己對這些面大小的估計是否準確;量一量，用1平方厘米的小正方形度量橡皮的一個面;鋪一鋪，用1平方厘米的小正方形來密鋪1平方分米的正方形;站一站，在1平方米大小的正方形紙上站一站，看看能站幾個小朋友。再如容積單位“毫升的認識”的教學，可以這樣安排：讓學生猜一猜，1毫升的水大概有多少;量一量，用量筒量出1毫升水;數一數，1毫升水有幾滴;玩一玩，把1毫升水倒在手心來感受;比一比，在杯子中倒入10毫升水，與1毫升水比一比。

長度單位、面積單位、體積單位等這些度量單位都是比較抽象的概念，所以教師在教學時更要提供多種實踐的機會，設置豐富的體驗活動。在動手操作的過程中，深度體驗度量，讓學生在多維的體驗活動中建立度量單位的表象，形成對度量單位的建模。

（三）加強聯系，在溝通中頓悟度量

數學的學習要從知識間的聯系去思考問題，度量的學習更不能孤立地進行。不同度量單位間的進率有差異，而且它們的教學零散地分布在不同的年級，所以學生對度量單位的掌握也是碎片化的，這樣的學習對學生造成很大困擾。因此，教師要從整體上進行溝通聯系，構建度量單位的知識網，讓知識變得更直觀、更有序。

例如在理解體積單位之后，可以進行長度、面積、體積單位之間的溝通整理教學，讓學生用手分別比畫出1厘米、1平方厘米、1立方厘米的大小。在比畫的過程中，引導學生去感受：三者所表示的形狀不同，意義也不同，1厘米是一條線，只需從一個方向進行比畫;1平方厘米是一個面，要比畫長和寬兩個方向;而1立方厘米是一個體，要比畫長寬高三個方向。然后復習長度單位間、面積單位間、體積單位間的進率，進而發現：兩個面積單位間的進率就等于相對應的長度單位間進率的平方，兩個體積單位的進率就等于相對應的長度單位間進率的立方。

數學知識是層層深入、不斷推進的過程，度量教學借助形來描述度量單位，找到它們的聯系與區別。從一維到二維再到三維，讓度量由線及面，面動成體，由體成系，在溝通中理解度量，掌握各度量單位之間的進率，能獲得理想的教學效果。

二、以數釋形，助推圖形計算板塊

圖形具有形象直觀的優點，所以不管是立體圖形的表面積和體積的計算，還是平面圖形的周長和面積的學習，在初學時都會給學生一種假象，讓他們覺得這些知識很簡單，易學，但等到知識一綜合，就會發現情況不妙了，周長與面積混淆了，表面積跟體積的內容又沒那么清晰了。光靠直觀的表象不能很好地解釋圖形里面蘊藏的本質，很難讓知識深刻。因此，教師要引導學生觀察各圖形的特點，溝通圖形之間的聯系，發掘里面的隱含信息，從“形”中抽象出“數”，以數釋形，讓直觀走向深刻（圖3）。這樣才能真正理解圖形計算，明白圖形計算的本質，讓圖形的計算落地生根。

（一）在對比中明理，讓算理更清晰

在圖形計算的教學中，不能讓學生直接進行計算公式的死記硬背。知識的混淆，究其原因，都是因為學生對概念的本質、方法的本質理解不清晰、不深刻。應加強對比教學，凸顯其本質特征。平面圖形之間、立體圖形之間都不是孤立存在的，這些知識相互關聯，有聯系又有區別。需要教師創設條件，組織學生在觀察中找到聯系，在不斷地對比中，總結方法，構建知識框架，梳理出知識脈絡。

“平行四邊形的面積”的教學，都是把“新知”平行四邊形轉化成“舊知”長方形（如圖4），左邊圖形是把平行四邊形“推拉”成長方形，右邊圖形是把平行四邊形“割補”成長方形，為什么一個不可以計算出平行四邊形的面積，一個卻可以？“推拉”“割補”后的圖形與原來的比較，什么沒變，什么變了？“推拉”之后，周長不變，面積變了，所以平行四邊形的周長=長方形的周長=（鄰邊+底）×2;“割補”之后，面積不變，周長變了，所以平行四邊形的面積=長方形的面積=底×高。

平面圖形、立體圖形相互之間都是有著內在聯系的，所以需要找到其中的連接點，不斷地對比學習。包括新知與舊知的對比學習，易錯點的對比學習，在對比學習中清晰概念，理解計算。

（二）在梳理中構建，讓方法聯成網

圖形計算的相關知識點分散在各個年級、各章節的教材中。教學時，教師應引導學生對圖形的特征進行觀察探究，讓學生感受圖形之間的聯系和區別，并經歷推導轉化的過程。以加強學生對圖形計算方法形成深刻體驗，在理解的基礎上進行計算方法的梳理、歸納、總結。還要貫通知識的前后聯系，注重知識之間的內在關系，溝通它們之間的區別與聯系，完善認知結構。在形的學習中抽象出數的規律，以數釋形。

從學生獨立整理的作品反饋中（圖5為其中之一），可以看出學生能對這些在不同時間段學習的平面圖形知識有序梳理，并進行溝通、聯系。由此可見平面圖形、立體圖形的學習，都需要通過一條主線將各知識點串起來，使之“豎成線”“橫成片”，形成知識網絡體系，構成完整的知識體系。

（三）在反思中內化，讓能力得升華

波利亞曾說：問題的解決只是數學研究工作的一半，更重要的是解題后的反思與回顧。任何知識都需要一個內化的過程，通過反思，能夠更深層次地理解知識，在不斷地反思中對圖形重新認識和理解，從而探尋出圖形計算的本質。

例如梯形面積的計算的教學，有了三角形面積計算的基礎，可讓學生將兩個完全一樣的梯形拼成一個大平行四邊形，再把大平行四邊形的面積除以2就是其中一個梯形的面積，所以梯形的面積=大平行四邊形的面積÷2=（上底+下底）×高÷2。公式的得到可以說是水到渠成，可在解決問題時，經常會有學生忘記除以2，所以在得出結論后，教師還要追問，以引發學生反思：“為什么要除以2？”“（上底+下底）×高計算的是什么？”“先算出上底加下底的和又是為什么？”在不斷追問中，回顧和思考剛才的學習過程，讓梯形面積的計算方法在反思中鞏固。有了這樣的討論和理解，后面當已知梯形的面積，計算梯形的高或上下底時，都要用梯形的面積先乘2，學生也能很快反應出“梯形面積乘2”這是算大平行四邊形的面積，再用這個面積除以底等于高，除以高等于底。有了這樣的經驗六年級學習圓錐的體積、計算圓錐的高，也就有基本的思維模式了。

任何學習都需要不斷回顧與反思，圖形的學習更甚，反思有助于圖形與算式的溝通，對圖形的理解更加深刻。反思更是為后面的學習提供更多的思維方式，有了這樣的思考習慣，圖形的學習會變得更加深刻。

三、數形互譯，助推解決問題板塊

數形結合思想是將抽象的數學語言與直觀的圖形結合起來解決問題的思想方法，通過數與形的互相轉化，把數與形統一起來。數形結合能使許多數學問題變得簡單、直觀。數形互譯能使“圖形的測量”板塊的教學問題解決變得簡單有趣，從而吸引學生主動參與解決問題的過程。

（一）以形表思，讓抽象問題直觀化

笛卡爾曾說：“沒有任何東西比幾何圖形更容易印入腦際了。因此，用這種方式來表達事物是非常有益的。”對于純文字的題目，借用圖形將關鍵信息表達出來，有助于更加有效地思考問題、分析問題，尋求解決問題的方法。

例如：一個圓柱的高是10厘米，如果高減少3厘米，那么表面積比原來減少94.2平方厘米。原來圓柱的表面積是多少平方厘米？教師講解時通過畫圖（圖6），學生很容易明白：94.2平方厘米就是減少部分的側面積。所以底面周長為94.2÷3=31.4（厘米），底面半徑為31.4÷3.14÷2=5（厘米），表面積為31.4×10+3.14×5×5×2=471（平方厘米）。再如推導圓柱體積公式時，教師把圓柱切拼成一個近似的長方體，切拼前和切拼后，體積不變。那表面積呢？增加了，增加了多少？通過圖形的幫助（圖7），學生就能發現增加的部分是兩個底面半徑乘高，也就是2rh。這樣把文字信息轉化成圖形的形式，可以讓思考有了拐杖，有了具體的表象，以形表思，讓解題思路一目了然，讓抽象問題直觀化。

（二）以數輔形，讓幾何問題代數化

圖形的知識可以通過數和計算幫助理解，還可以由算式探究圖形蘊含的規律，增進學生對圖形的理解。在教學中，通過觀察、找規律、歸納等方法，可以尋找出解決問題的數量關系式，使幾何問題代數化。以數輔形，用代數的方法使問題能更順利地得到解決。

例如計算多邊形的內角和，可從一個頂點出發畫對角線把多邊形分成若干個三角形，分成了幾個三角形，就是幾個180°，由此可以求出多邊形的內角和。再通過畫圖，找到其中的規律，學生就會發現三角形個數跟邊數之間是有關系的，多邊形內角和=（多邊形的邊數-2）×180°，為問題的解答找到了更簡便的方法。如圖8，已知正方形OABC的面積是10平方厘米，求圓的面積。按常規思路，求圓的面積，我們需要知道圓的半徑。可是僅從小學的知識儲備，不能算出半徑的長度。但已知正方形的面積是10平方厘米，從圖可以看出正方形的邊OA、OC都是圓的半徑，所以半徑的平方就等于10平方厘米。圓的面積等于半徑的平方乘圓周率，也就不需要算半徑是多少，圓的面積就等于10×3.14=31.4平方厘米。

可見根據已知的圖形信息和圖形本身的特點，尋找其中的關聯，將圖形問題轉換為代數問題，實現由形到數的轉化，讓問題解決更加快捷、準確。

（三）數形互通，讓方法技能靈動化

數形結合能使隱藏的數量關系變得直觀，能將淺顯的圖形問題變得深刻，在解決問題時應不斷嘗試，學會將數學語言與直觀的圖形語言進行轉換。

如圖9，密閉容器中的水，若倒過來，水面的高度是多少？從圖中，可以知道現在水的高度是23厘米，由等底的圓柱和圓錐組成，其中圓錐的高為18厘米，所以計算得出圓柱的高為23-18=5（厘米）。若倒過來，那么圓柱部分形狀不變，可是圓錐部分將變成一個跟現在等底的圓柱。因為等底等體積的圓柱與圓錐，它們的高是3倍的關系，所以新圓柱的高為18÷3=6（厘米），所以水的高度為5+6=11（厘米）。

數形結合能使數量之間的內在聯系變得直觀，使復雜問題簡單化，抽象問題具體化，因此，在問題解決教學中，應使學生感受數形結合的優勢，并培養他們數形結合的思想，提升他們解決問題的能力。

綜上所述，在“圖形的測量”板塊教學時，通過數形結合思想，在數與形之間搭建腳手架，讓數形結合成為“圖形的測量”教學的助推器。幫助學生準確理解圖形的本質，積極探討數與形之間的數學聯系，讓數直觀，讓形入微。教師需要不斷提高自身的素養，研究相關的理論，做教學的有心人，挖掘數形結合點，設計科學有效的教學活動，引導學生建立空間思維，培養學生的數學核心素養。

作者簡介：金姻脂（1983—），本科學歷，一級教師，溫嶺市名師，從事小學數學教學工作。