小學生數學基本活動經驗的積累研究

[摘? 要] 研究者以自身的具體教學實踐為例，提出“適切的情境”“開放性的探究活動”和“具體的實際應用”三個積累數學基本活動經驗的途徑，確保學生在親身經歷中積累更多的直接經驗、間接經驗和思維經驗，從而使學生的能力在經驗的積淀中獲得更多的提升。

[關鍵詞] 數學基本活動經驗;直接經驗;間接經驗;思維經驗

傳統課堂教學中，教師好似演員，整節課不停地表演，使得講解和分析占據整個課堂;而學生好似觀眾，只需“靜坐觀課”，很少主動參與知識的探究與學習。在這樣的教學模式下，學生只能掌握數學知識的“皮毛”，無法真正領悟知識的內涵與外延，更不要說靈活運用知識了。

新課程強調的是學習方式的變革，倡導學習主體的轉變，給予學生足夠的時空思考數學問題，研究數學邏輯，探索數學奧秘，交流數學應用，如此靈動的數學課堂，需要學生具有一定的“經驗”。因此，教師應設計適切的教學活動，讓學生親歷操作、思考和探究，實現從感性認識到理性認識的飛躍，使得活動經驗的內涵越發豐富，從而積累充足而有效的活動經驗。下面筆者以自己的具體教學實踐為例，從多個角度著手談談在教學中積累基本活動經驗的教學思路。

一、依托適切的情境，積淀直接經驗

1. 游戲情境

喜歡游戲是兒童的天性，教師設計數學活動可以將游戲融入其中，為數學知識增添活力，為數學課堂增添生機，這樣則可激發小學生的學習興趣，使其興致勃勃地參與活動，獲得直觀體驗，自主地吸收活動經驗，有效地積淀直接經驗。

案例1? 立體圖形的認識

游戲情境：找朋友

（1）請帶著長方體、正方體、圓柱、球的4名學生先到講臺上來。

（2）請大家帶著你帶來的生活用品依次到講臺上來“找朋友”。

（3）請找到朋友的學生說一說，為什么你們是“朋友”。

（4）摸一摸你的“朋友”，并說一說它們有何特征。

設計意圖：通過“找朋友”的游戲情境進行切入，使得枯燥的數學知識變得生動，使得數學概念融于學生喜聞樂見的游戲中，豐富他們的內心體驗，讓學生用多感官去感知各種立體圖形的形狀特征，從而探尋到立體圖形的本質，自然地積淀直接經驗。

2. 操作情境

活動經驗的積淀與數學知識的學習密不可分，而積累活動經驗必須讓多感官參與其中，學生在手、口、腦的參與下才能豐富操作經驗。基于此，教師應提供豐富的素材去設計和構造操作活動，幫助學生積淀直接經驗。

案例2? 分數的初步認識

活動1：取出準備好的長方形紙片，通過折和涂，表示出它的1/2。

要求：同桌兩人一組應生成不同的折法，并交流“它的1/2是如何得到的”。（學生積極投入操作，直觀感受1/2，同桌兩人交流折法，并在思考與交流后有了一定的認識）

活動2：是否還存在其他不同的表示方法？（為了讓學生疊加體驗，又一次開展了更加深入的操作活動）

活動3：試著通過折和涂，表示出長方形、圓形和等邊三角形的1/2。（以問題引導學生繼續折和畫，以外顯的行為操作，深化學生對分數本質的理解）

設計意圖：以操作情境為指引，在輕松愉悅的課堂氛圍中讓學生自主探究和合作交流，進一步明晰“分數的本質屬性是無論圖形如何變化，只需將其平均分成2份，其中的任意一份就是它的1/2”。這樣的活動過程耗時不多，但學生在動手、動腦和動口中愉快體驗，獲得了更加形象的分數概念，并為進一步探索1/4、1/8等分數的本質特征奠定了操作基礎，積淀了直接經驗。

二、依托開放性的探究活動，積累間接經驗

間接經驗的獲取直接指向問題的解決，它需要的是一種開放的、創造性的活動，讓學生在活動中有經歷、有體驗、有數學思考，這樣才能實現對經驗的獲取與積累。因此，教師應時常拋出特定情境下的特定問題，組織適度的開放性的探究活動，激發學生的探究意識，讓學生進行外顯的行為操作與思維層面的操作活動，積累充分而有效的間接經驗。

案例3? 三角形三邊的關系

活動1：試著用3根小棒圍出一個三角形，并思考任意的三根小棒都可以嗎？

活動2：用四組長度不同的小棒驗證剛才的猜想，并說一說你的發現。（學生經過探究與交流，很快有了新的發現）

活動3：是否只需要兩根小棒的長度之和大于另一根小棒，就能圍成三角形呢？請再一次通過操作進行驗證。

設計意圖：整個探究活動的設計環環相扣，為學生的主動探究搭起了橋梁，不斷促進思考的深入。此時的操作與探究成了學生自主的需求，由于學生對探索的結果充滿渴望，因此在探究活動中，學生所積累的經驗也會因個體的強烈感知而更具有生命活力。就這樣，既有獨立思考的成分，又有合作學習的融入，新知在操作中變得清晰，在數學思考中逐步深入，逐漸形成間接經驗。

三、依托具體的實際應用，增強思維經驗

思維經驗的積累是伴隨著思維活動的過程而產生的，但這樣的認知體驗是碎片式的，也是不穩定的。因此，教師需要在教學中有意識地固化學生的認知體驗，讓學生最終形成根深蒂固的思維經驗。依托具體的實際應用可以幫助學生構建“思維鏈”，這對于思維經驗的積累十分有益。在問題解決的過程中激活已有的“思維經驗”，在反思活動中進行經驗的整合，并逐步形成新的“思維經驗”，進而增強思維經驗。

案例4? 找規律

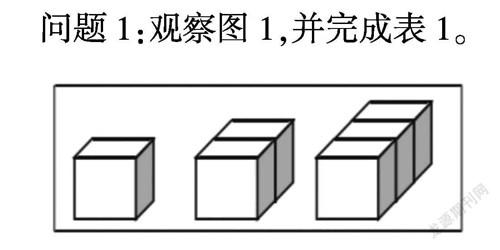
問題1：觀察圖1，并完成表1。

（在直接經驗的影響下，學生借助圖形輕松且快速地完成了表格的填寫。）

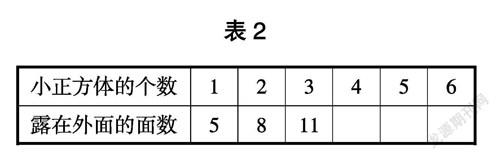
問題2：結合問題1的圖示與表格，繼續完成表2。

（在直接經驗的基礎之上，融合間接經驗，學生完成了表2的填寫）

問題3：當小正方體的個數逐步增加到n個時，露在外面的面數又會是多少？

（此問題雖難度較大，但學生也能從直接經驗與間接經驗中找到方法，教師拋出這一問題后應大膽放手，讓學生進行深層次的思考。學生深入觀察圖1，在經歷思考、探究、討論、思辨后可以得出“圖1中的三個圖的前后面露在外面的面數都是1;除去這兩個面，每個小正方體的上面、左面和右面也露在外面”，進而得出：1個小正方體露出的面數是3×1+2，2個小正方體露出的面數是3×2+2，3個小正方體露出的面數是3×3+2”。以此類推，可以得出n個小正方體露出的面數是3×n+2。）

設計意圖：為了解決找規律問題，教師采用了層層遞進的思路，幫助學生感受規律，化解對這類問題的疑慮，實現讓學生掌握解決這類問題的方法的教學目標。本設計旨在引導學生經歷問題探究從低維到高維的升級過程，讓學生產生拓展思維空間的主觀愿望，在輕松愉悅的小組合作學習中找尋規律，從而獲得對規律問題的全新理解，積累解決問題的方法，發展抽象思維能力。

總之，數學活動經驗的積累需要教師在日常教學中一以貫之地提供“源泉”。從適切的情境的創設、開放性的探究活動和具體的實際應用的設計著手，基于教學內容與學生實際，促使學生產生思維的碰撞，讓學生在親身經歷中積累更多的直接經驗、間接經驗和思維經驗，使學生的能力在經驗的積淀中獲得更大的提升。

作者簡介：王靜（1993—），教育學碩士，小學二級教師，從事小學數學教學工作，曾獲江蘇省教師現代教育技術應用作品大賽二等獎、江蘇省藍天杯教學設計二等獎。