單位圓在三角函數教學中的作用

摘要：將單位圓融入三角函數教學，能夠令抽象難懂的三角函數知識變得形象直觀，從而易于學生理解，簡化教學過程，優化教學效果.

關鍵詞：單位圓;三角函數;教學;輔助作用

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2022）28-0104-03

收稿日期：2022-07-05

作者簡介：郭芳麗（1965.4-），女，陜西省西安人，中學高級教師，從事高中數學教學研究.

在初中，我們利用直角三角形學習了銳角三角函數；到了高中，為進一步研究任意角的三角函數，需要借助單位圓.單位圓簡單直觀，具有圓的對稱性和旋轉不變性，三角函數有了單位圓的加入，便展開了一系列行之有效的教學活動.

1 理解弧度制

在高中階段，弧度制的學習是一個難點，為了突破這個難點，我們借助單位圓來直觀理解.如圖1，在單位圓中，長度為1的弧AB所對的圓心角∠AOB就是1弧度角.“弧度制”是用弧的長度來度量角的大小，弧度制統一了角度與長度的單位.

在講解角的集合與實數集對應關系的過程中，引入（如圖2所示）單位圓模型：讓單位圓M與數軸相切于原點O，把數軸看成一個皮尺， 對于任意一個正數a，它對應數軸上的點A，把線段OA逆時針方向纏繞到單位圓M上，點A對應單位圓上的點 A′，這樣以MO為始邊，經逆時針方向旋轉以MA′為終邊的圓心角α的弧度數為正數a；同樣對于任意一個負數b，對應數軸上的點B，將線段OB順時針方向纏繞到單位圓M上，點B對應單位圓上點B′，則以MO為始邊經過順時針方向旋轉以MB′為終邊的圓心角β的弧度數為負數b.

2 定義任意角的三角函數

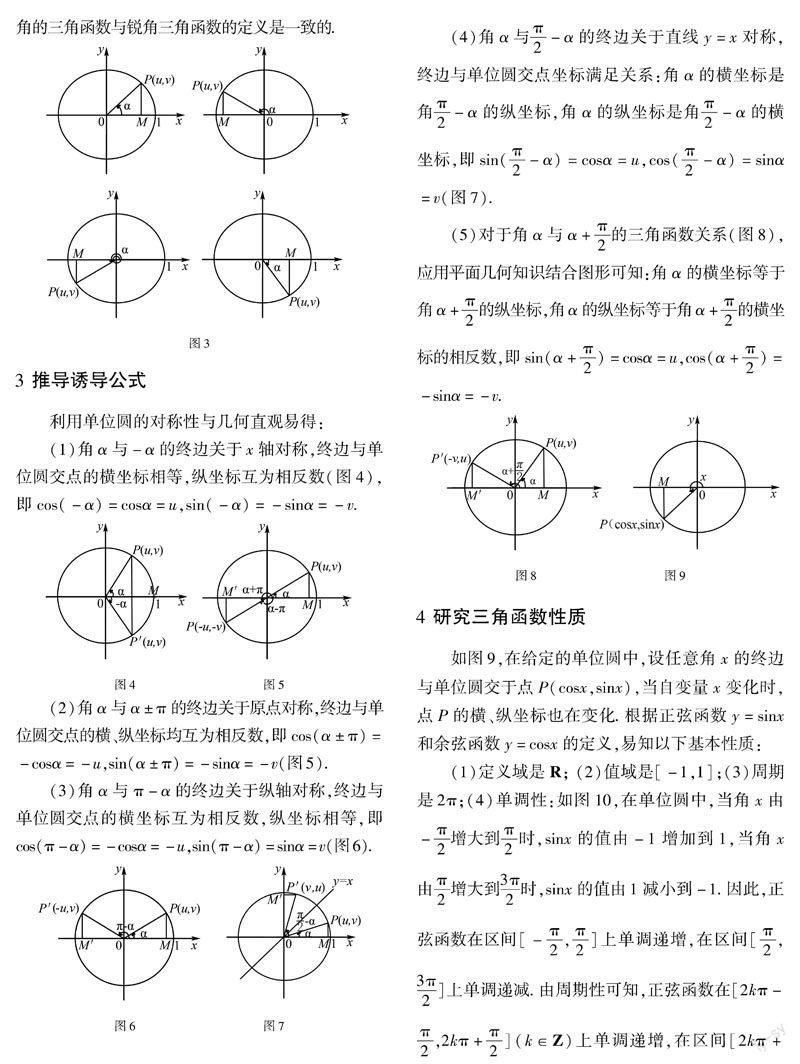
如圖3，在直角坐標系的單位圓中，用角α的終邊與單位圓交點p（u，v）的縱坐標v、橫坐標u分別定義角α的正弦函數和余弦函數，記作v=sinα和u=cosα；比值

vu定義為角α的正切函數，記作

vu=tanα，其中

α∈R，α≠π2+kπ，k∈Z.用單位圓定義任意角的三角函數與銳角三角函數的定義是一致的.

3 推導誘導公式

利用單位圓的對稱性與幾何直觀易得：

（1）角α與-α的終邊關于x軸對稱，終邊與單位圓交點的橫坐標相等，縱坐標互為相反數（圖4），即

cos（-α）=cosα=u，sin（-α）=-sinα=-v.

（2）角α與α±π的終邊關于原點對稱，終邊與單位圓交點的橫、縱坐標均互為相反數，即cos（α±π）=-cosα=-u，sin（α±π）=-sinα=-v（圖5）.

（3）角α與π-α的終邊關于縱軸對稱，終邊與單位圓交點的橫坐標互為相反數，縱坐標相等，即

cos（π-α）=-cosα=-u，sin（π-α）=sinα=v（圖6）.

（4）角α與π2-α的終邊關于直線y=x對稱，終邊與單位圓交點坐標滿足關系：角α的橫坐標是角

π2-α的縱坐標，角α的縱坐標是角π2-α

的橫坐標，即sin（π2-α）=cosα=u，cos（π2-α）=sinα=v（圖7）.

（5）對于角α與α+π2

的三角函數關系（圖8），應用平面幾何知識結合圖形可知：角α的橫坐標等于角α+π2的縱坐標，角α的縱坐標等于角α+π2的橫坐標的相反數，即sin（α+π2）=cosα=u，cos（α+π2）=-sinα=-v.

4 研究三角函數性質

如圖9，在給定的單位圓中，設任意角x的終邊與單位圓交于點P（cosx，sinx），當自變量x變化時，點P的橫、縱坐標也在變化.根據正弦函數y=sinx和余弦函數y=cosx的定義，易知以下基本性質：

（1）定義域是R;

（2）值域是［-1，1］；

（3）周期是2π；

（4）單調性：如圖10，在單位圓中，當角x由

-π2增大到π2時，sinx的值由-1增加到1，當角x由π2增大到

3π2時，sinx的值由1減小到-1.因此，正弦函數在區間［-π2，π2］上單調遞增，在區間［π2，3π2］上單調遞減.由周期性可知，正弦函數在［2kπ-π2，2kπ+π2］（k∈Z）上單調遞增，在區間［2kπ+π2，2kπ+π2］（k∈Z）

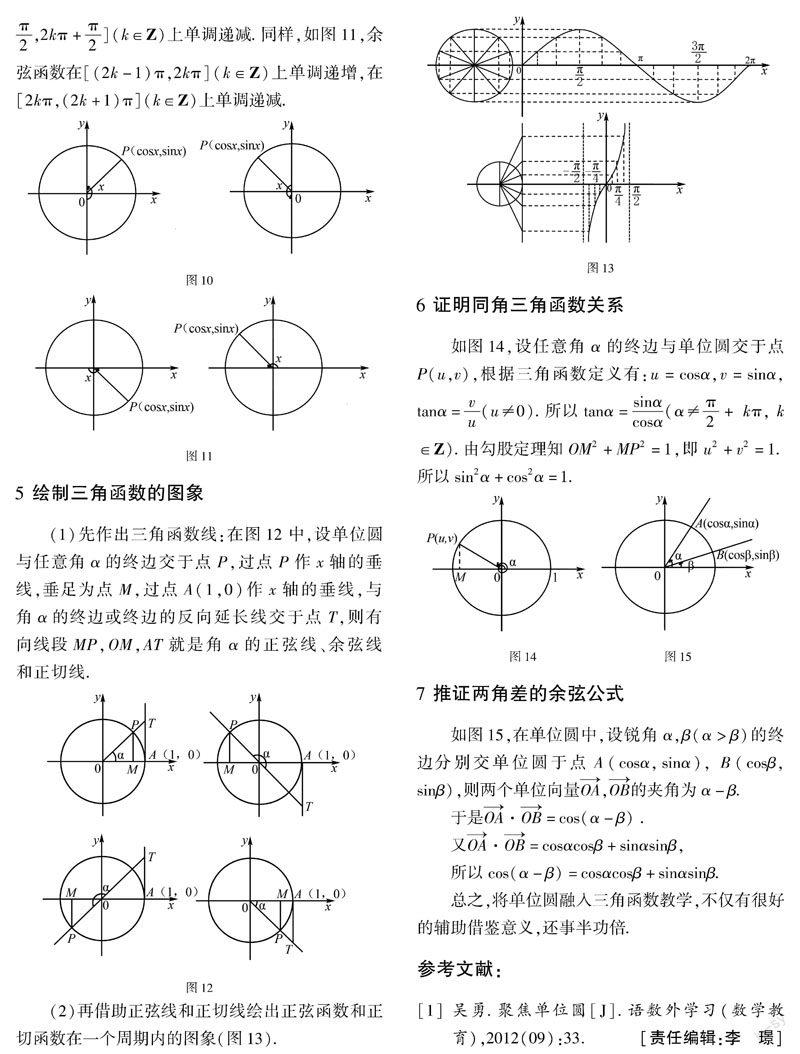
上單調遞減.同樣，如圖11，余弦函數在［（2k-1）π，2kπ］（k∈Z）上單調遞增，在［2kπ，（2k+1）π］（k∈Z）上單調遞減.

5 繪制三角函數的圖象

（1）先作出三角函數線：在圖12中，設單位圓與任意角α的終邊交于點P，過點P作x軸的垂線，垂足為點M，過點A（1，0）作x軸的垂線，與角α的終邊或終邊的反向延長線交于點T，則有向線段MP，OM，AT就是角α的正弦線、余弦線和正切線.

（2）再借助正弦線和正切線繪出正弦函數和正切函數在一個周期內的圖象（圖13）.

6 證明同角三角函數關系

如圖14，設任意角α的終邊與單位圓交于點

P（u，v），根據三角函數定義有：u=cosα，v=sinα，tanα=vu（u≠0）.所以tanα=sinαcosα（α≠π2+ kπ， k∈Z）.由勾股定理知OM2+MP2=1，即u2+v2=1.所以sin2α+cos2α=1.

7 推證兩角差的余弦公式

如圖15，在單位圓中，設銳角α，β（α>β）的終邊分別交單位圓于點A（cosα，sinα）， B（cosβ，sinβ），則兩個單位向量OA，OB的夾角為α-β.

于是OA·OB=cos（α-β） .

又OA·OB=cosαcosβ+sinαsinβ，

所以cos（α-β）=cosαcosβ+sinαsinβ.

總之，將單位圓融入三角函數教學，不僅有很好的輔助借鑒意義，還事半功倍.

參考文獻：

［1］吳勇.聚焦單位圓[J].語數外學習（數學教育），2012（09）：33.