小學數學教學中“合作學習單”的設計與使用

凌建青，陳希文

摘要：小學數學教學中，教師可通過選取教材中適合學生合作學習的內容，以“合作學習單”的形式呈現合作學習任務，使學生明確學習的內容、程序，反饋學習結果，讓學生在小組合作學習的活動中，發現數學知識，解決數學問題，發展數學素養。作為其關鍵，設計和使用“合作學習單”要在把握目標價值、觀照構成要素的基礎上，選擇恰當的時機，比如動手操作的材料豐富可選時、解決問題的方法靈活多樣時、思考探究的難度容量較大時等。

關鍵詞：小學數學;合作學習;合作學習單

合作學習是數學課程標準提倡的重要的學習方式之一。教師通過選取教材中適合學生合作學習的內容（素材），布置合作學習任務，讓學生在小組合作學習的活動（過程）中，發現數學知識，解決數學問題，發展數學素養。

如何保證小組合作學習有序、有效地展開？“合作學習單”的引領起著至關重要的作用。所謂“合作學習單”，是指在學生以小組為單位開展合作學習時，使學生明確學習內容和程序、反饋學習結果的功能性菜單。它的設計與使用，要綜合教師對教材的解讀，顧及學生的認知特點，遵行一定的原則，講究一定的策略。就小學數學教學中“合作學習單”的設計和使用，談一些筆者的思考與實踐。

一、“合作學習單”的目標價值

無論在何種合作學習的情境下使用“合作學習單”，目的都是保證小組合作的效率大于個人的“單打獨斗”。首先，“合作學習單”的設計要讓小組的所有成員有自己的任務——任務讓學生能參與。其次，“合作學習單”的設計要讓小組的所有成員有共同的目標——目標讓學生有動力。雖然小組成員因為合作的需要，所需完成的任務不盡相同，但所追求的目標是一致的：合力解決小組共同的任務。再次，為了保證小組成員之間的有效互動，“合作學習單”中的學習任務除了要責任到人，更要實現積極“互賴”。所謂“互賴”，一是要求所有組員學會完成布置給自己的任務，二是確保所有組員掌握布置給其他組員的材料。

通過合作學習，學生可以合力突破學習重難點、解決問題，在知識和技能等方面獲得提升。但是從學生發展的角度來說，這只是“合作學習單”的使用價值之一。“合作學習單”不僅是一張學習任務單，更能在組織學生有效合作的過程中，培養學生的合作意識和合作能力，從而提升學生的合作品質——讓學生在解決問題、學習知識和技能的同時，學會傾聽與表達、認可和信任、接納和支持等。比如，提出“幫助小組內有困難的同學共同完成”“讓‘弱者先說”“給予贊美和鼓勵”等要求，來改變傳統學習過程中只注重學生之間競爭關系的局面。

二、“合作學習單”的構成要素

“合作學習單”一般包含三個要素：一是明確的學習內容，二是規范的學習程序，三是小組成員的學習反饋。明確的學習內容就是告知學生做什么。合作學習不同于獨自學習，不僅要讓小組成員知道自己做什么，更要讓小組成員知道共同的目標是什么。規范的學習程序就是告訴學生先做什么，再做什么，保證學生的學習循序漸進地進行。比如，先個體獨立思考，再小組成員之間合作交流。學習反饋是在做什么、怎么做的基礎上，促進學生面對面地互動交流——既可以是問題的提出，也可以是成果的匯報;既可以是見解的辨析，也可以是結論的發現，等等。當然，有時為了更好地保證合作學習的開展，也可依據具體的學習內容設定合作時間，作為“合作學習單”的第四個要素。

例如，教學蘇教版小學數學四年級下冊《認識三角形》一課時，設計的“合作學習單”內容如下：

1.小組分工，每人選擇一種材料（釘子板、小棒、扇形紙片、方格紙等），通過圍一圍、擺一擺、剪一剪或畫一畫等方式做一個三角形。

2.在小組里討論三角形有什么特征。

3.推薦組員代表小組進行全班交流。

這一“合作學習單”，明確了每個小組成員要“選擇一種材料做一個三角形”，整個小組要“探究三角形的特征”;規范了學生先通過圍一圍、擺一擺、剪一剪或畫一畫獨立探究，積累基本活動經驗，再在小組內合作交流，形成一致的觀點，然后全班匯報。同時，要求學生進行兩次學習反饋：一是組內交流自己做三角形的體會，如圍三角形的學生可指出三角形有三條邊、三個角、三個頂點，擺三角形的學生可指出三條邊要首尾相接，剪三角形的學生可指出三條邊是直的;二是全班交流三角形的特征，目的是形成共識，即三角形是由三條線段首尾相接圍成的平面圖形。

三、“合作學習單”的設計與使用要把握時機

合作學習作為一種學習方式和教學策略，是教師根據教學內容、教學目標和學生的學習需要擇機而定的。因此，“合作學習單”的設計和使用要選擇恰當的時機。

（一）動手操作的材料豐富可選時

盡管有些動手操作可以讓學生獨立完成，但是更多的動作操作，特別是材料豐富可選的動手操作，可以小組合作的形式展開，從而保證學生充分參與學習過程，深刻理解學習結果。

例如，教學蘇教版小學數學四年級下冊《認識平行四邊形》一課時，為了讓學生更好地理解平行四邊形的對邊相等且平行，在學生從生活實物中抽象出平行四邊形后，增設一個動手操作的小組合作學習活動，讓學生經歷“做數學”的過程，在積累豐富的數學活動經驗的同時，發現平行四邊形邊的特征。設計的“合作學習單”內容如下：

1.以4人小組為單位，組長分工，每人選擇一種材料（釘子板、兩塊相同的三角板、小棒、方格紙等），通過圍一圍、拼一拼、搭一搭或畫一畫等方式做一個平行四邊形。

2.幫助小組內做平行四邊形有困難的同學完成。

3.小組內輪流說一說：平行四邊形的邊有什么共同的特點？

本次合作學習中，小組成員之間存在良好的互動。比如，一位學生選擇的是用兩塊相同的三角板拼一個平行四邊形，但是沒有拼成，經過小組內其他成員的幫助，最終順利完成了“做一個平行四邊形”的任務。從小組成員對“平行四邊形的邊有什么共同的特點”的交流反饋中可以看出，學生有自己做平行四邊形和觀察其他成員做平行四邊形的兩次經歷，對平行四邊形邊的特征有了不同層次的感受。用小棒搭成平行四邊形的學生依次指著左右和上下兩條邊說：“這兩條邊一樣長，這兩條邊也一樣長。”用兩塊相同的三角板拼成平行四邊形的學生指出：“上面和下面的兩條邊相等，左面和右面的兩條邊相等。”在方格紙上畫出平行四邊形的學生補充：“平行四邊形的上下兩邊互相平行。”

縱觀本次動手操作，學生按照“合作學習單”設計的學習程序，通過個體的獨立思考以及同伴的互相幫助，用不同的材料做出了平行四邊形，并圍繞平行四邊形邊的特點進行了有效的交流，小組合作取得了預期的成效。

（二）解決問題的方法靈活多樣時

小學數學中，有很多問題的解決方法靈活多樣。對此，可以讓學生小組合作探究，拓寬思路，多角度、多側面地認識問題，提出多種不同的解題方法，從而培養學生思維的敏捷性、發散性和創造性。

例如，教學蘇教版小學數學六年級下冊《解決問題的策略》一課時，出示改編自教材例1的題目：已知美術組一共有35人，男生人數是女生的23，則美術組的男、女生各有多少人？這是一道稍復雜的分數應用題，學生在先前的學習中已經具備了解決此類問題的經驗，而且解題方法比較多樣。這里引入合作學習方式，便于學生對不同解法的交流與理解。設計的“合作學習單”內容如下：

1.根據題目中的條件和問題，每位組員選擇1—2種方法解答。

2.每個人在小組內輪流說出自己解題的思路，盡可能讓所有組員都理解。

3.比一比：不同的方法有什么相同的地方？

有的學生根據“男生人數是女生的23”這個條件畫線段圖，看出男生人數是美術組總人數的25，將原來的問題轉化成：美術組一共有35人，男生人數是總人數的25，女生人數是總人數的35，男、女生各有多少人？這是簡單的“求一個數的幾分之幾是多少”的問題。有的學生根據“男生人數是女生的23”，推理出“男生人數和女生人數的比是2∶3”，將原問題轉化成：美術組一共有35人，男生與女生人數的比是2∶3，男、女生各有多少人？這是按比例分配的問題。有的學生根據“男生人數是女生的23”，想到“女生人數是3份，男生人數是2份”，先算出1份是幾人，再算出2份、3份各是多少人。還有的學生根據“男生人數是女生的23”，把作為單位“1”的女生人數設為x，那么男生人數就是23x，然后利用“美術組一共有35人”，列方程解題。

本次合作學習中，每位小組成員在獨立思考后，都能基于自己的個性化理解，至少想出一種解決方法，并將思考的過程頭頭是道地說給組員聽，不僅促成了有效的互動，更實現了真正意義上的思維發散和方法互補。在此基礎上，通過“不同的方法有什么相同的地方”的討論，學生自然而然地體會到了雖然方法不同，但是殊途同歸，都運用了“轉化”的策略。

（三）思考探究的難度容量較大時

學習理論表明，合作學習小組面對的問題越具有挑戰性，小組成員共同努力的動機越強烈。小學數學中，有一些知識（問題）的發現（解決），對于學生來說有較大的挑戰性，大部分學生獨立思考探究有困難。對此，教師可以組織學生合作學習，借助集體的力量，促進思維碰撞，不斷深入，共同攻堅克難。

例如，教學蘇教版小學數學五年級下冊《3的倍數特征》一課時，為了幫助學生發現（理解）“若一個數各個數位上數的和是3的倍數，則這個數是3的倍數”這一結論（難點），設計如下“合作學習單”內容，引領學生開展合作學習：

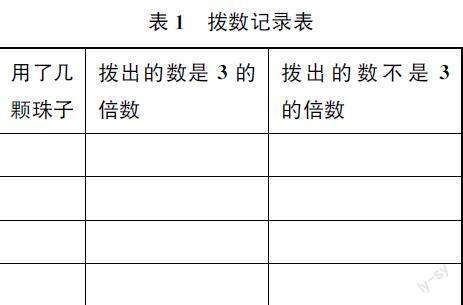
1.組長分工，每人選擇不同的珠子數，在計數器上撥數，判斷撥出的數是不是3的倍數（可用計算器），并將結果記錄在表格（如表1）中。

2.輪流說一說：用怎樣的珠子數撥出的數是3的倍數？

3.小組討論：3的倍數有什么特點？

為了探索3的倍數特征，小組成員按照“合作學習單”規定的學習程序，不斷地“試驗”不同數量的珠子，判斷撥出的數是不是3的倍數。組內成員人人參與，又都有各自的“小發現”：用3、6、9等3的倍數顆珠子時，撥出的數是3的倍數;否則，撥出的數不是3的倍數。將“小發現”匯總在表格中，便有了3的倍數特征的“大發現”：若一個數各個數位上數的和是3的倍數，則這個數是3的倍數。

整個合作學習過程在“合作學習單”的引領下順暢且嚴謹，小組成員都貢獻了自己的成果，不僅研究了正例，而且研究了反例，得到的結論站得住腳。整個探究過程符合小學生的認識規律，將各個數位上數的和與撥的珠子數建立聯系，借助直觀形象走向抽象與歸納。