放手讓學生自選條件計算圓柱的表面積
明啟文
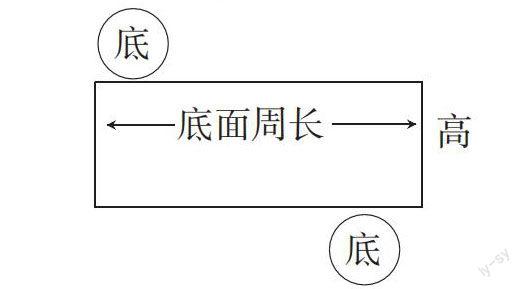

圓柱的展開圖是一個組合圖形,計算圓柱的表面積實際就是計算這個組合圖形的面積,組合圖形的面積學生會計算,因此,教學時可以放手讓學生自選條件計算圓柱的表面積;課本上第22頁的例4可以讓學生自學理解;練習題也讓學生獨立審題,找出解題須理解和突破的小障礙,這樣,課堂上學生積極地進行思維,主動地參與學習,收獲會更大。
教學開始,由復習逐漸引入新課。師:上節課我們學習了圓柱的認識,你們能不能畫出圓柱的展開圖?(能!)請你們在草稿本上畫出來,并標出各部分的名稱。全班在草稿上畫,抽生上黑板上畫,改正后得到:
師:今天我們學習“圓柱的表面積”(板書),圓柱的表面積指的是哪部分的面積?(生:就是展開圖中一個長方形和兩個完全相等的圓的組合圖形)
師:組合圖形的面積你們會算嗎?(會!)
師:假如在這個組合圖形中,我只告訴你兩個最基本的條件,讓你計算圓柱的表面積,你需要哪兩個條件?
學生經過思考后,有人提出:我需要底面半徑和圓柱的高;有人提出:我需要底面的直徑和圓柱的高;還有人提出:我需要底面周長和圓柱的高。接著老師布置練習:需要底面半徑和圓柱的高的做第23頁練習四第6題的第3圖(r=5cm,h=12cm);需要底面直徑和圓柱的高做第23頁練習四第1題的第3圖(d=18cm,h=15cm);需要底面周長和圓柱的高的做這個:C=6.28dm,h=7dm。學生開始根據給定的條件進行計算,每個人必須選擇其中的兩種情況進行解答。(要求分步解答)
抽生到黑板上解答,并講解,這樣便依次得到:
a:已知r=5cm,h=12cm。
①先算兩個底面的面積:2πr2=2×3.14×52=157(cm2);
②求底面周長:2πr=2×3.14×5=31.4(cm);
③求這個長方形的面積(圓柱的側面積):Ch=31.4×12=376.8(cm2);
④求圓柱的表面積:157+376.8=533.8(cm2)。
b:已知d=18cm,h=15cm。
①先求半徑r=d÷2=18÷2=9(cm);
②再求兩個底面的面積:2πr2=2×3.14×92=508.68(cm2);
③求底面周長:πd=3.14×18=56.52(cm);
④求圓柱的側面積:Ch=56.52×15=847.8(cm2);
⑤求圓柱的表面積:508.68+847.8=1356.48(cm2)。
c:已知C=6.28dm,h=7dm。
①先求側面積:Ch=6.28×7=43.96(dm2);
②再求底面半徑:=6.28÷(2×3.14)=1(dm);
③求兩個底面的面積:2×3.14×12=6.28(dm2);
④求圓柱的表面積:43.96+6.28=50.24(dm2)。
學生的解答是正確的,講解的層次也是清晰的。這時老師提問:在你們需要的條件中,哪一個條件是必須具備的?為什么?(經過學生的發言和討論,可得到:圓柱的高是必須具備的條件,因為計算圓柱的側面積時需要用圓周長和高相乘,別的條件是代替不了“高”的。到于底面積和底面周長,只要知道底面的半徑、直徑或周長中任意一個條件,便可推導轉換得到。)師:你們覺得這3個條件,知道哪一個計算起來更容易一些?知道哪一個計算起來難一點?(學生紛紛發表看法,討論總結為:已知底面的半徑,計算起來容易一些,因為無論是計算底面的周長或者面積,都可以直接代公式;已知周長時,計算底面積時,需用r=先求出半徑,這種難一點。根據學生的發言和討論,可得到如下的板書:
師:同學們可根據不同的條件,求出完整的圓柱的表面積。其實在我們生活中,有時并不需要求完整的圓柱的表面積,解題要認真分析,請大家翻開課本第22頁,自學例4。(學生自學例4)
待學生學完后,提問:(1)要求做一頂廚師帽的面料要多少,實際是求什么?(生:實際是求圓柱的表面積,這個圓柱因為是帽子,所以只有一個底面。)(2)你們能不能說一說解答的步驟?(生:能。①求側面積:3.14×20×30=1884(cm2);②求帽頂的面積:3.14×(20÷2)2=314(cm2);③需要多少面料:1884+314=2198≈2200(cm2)師:計算的結果是2198,是一個準確數,你是采用什么方法處理后得到一個近似數2200呢?(是用“進一法”處理的,根據實際不需要百位以下的數,所以百位以下的數學,不論大小,統統去掉,但要在百位上進一。)(3)本題的答案為什么采用“進一法”取近似數?(生:因為實際使用的面料要比計算的結果多一些)(4)你認為是多在哪里?(學生無言可對,老師用草圖幫助理解:a.縫制時接頭處 布料是重疊使用的;b.裁剪帽頂會出現邊角廢料)
練習。下面的題請先審題,讀題后發表自己的意見:提醒大家解題時要注意什么?
1.課本第23頁練習四第2題:“一臺壓路機的前輪是圓柱形,輪寬2m,直徑1.2m。前輪轉動一周,壓路的面積是多少平方米?”(生提醒:實際是求圓柱的側面積,不包括兩個底面)
2.課本第23頁練習四第3題:“修建一個圓柱形沼氣池,底面直徑是3m,深2m。在池的側面與下底面抹上水泥。抹水泥部分的面積是多少平方米?”(生提醒:實際上是求圓柱的表面積,但只有一個底面)
3.課本第24頁練習四第8題:“王阿姨做了一個圓柱形的抱枕,長80cm,底面直徑18cm。如果側面用花布,底面用黃色的布,兩種布各需要多少?”(生提醒:此抱枕是一個完整的圓柱,計算所用的布料,是求表面積,但所提的問題是:“兩種布各需要多少?”因此,兩個底面的面積和側面積分開計算后,不要相加,要分開回答。計算結果要采用“進一法”處理)
4.課本第24頁練習第13題:“一根圓柱形木料的底面半徑是0.3m,長是2m。如下圖所示,將它截成4段,這些木料的表面積比原木料增加了多少平方米?”
(生提醒:從圖上看截成4段,實際上是截(鋸)了3次,每鋸一次就增加兩個底面,鋸了3次就增加了6個底面的面積。題中的“長是2m”與解題無關,是多余條件)
經過學生的討論提醒后,然后讓學生解答練習。

