考慮附加抗力影響的單樁水平受力分析方法

黃 申，翟恩地,2，許成順，孫毅龍

(1. 北京工業大學城市與工程安全減災教育部安全實驗室，北京100124；2. 新疆金風科技股份有限公司，北京100176)

近年來，單樁基礎已廣泛應用于橋梁、高層建筑和海上風電等工程中。在單樁基礎的眾多水平承載特性分析模型中，傳統的Winkler 地基梁模型由于其原理簡單，結合現有的p-y曲線和t-z曲線研究成果，在工程設計中得到廣泛應用。隨著樁徑的逐漸增大，樁側摩阻力和樁端阻力對單樁水平承載特性的影響越來越顯著，國內外眾多學者對此展開研究。

Alikhanlou[1]針對剛性單樁基礎提出五彈簧模型，該模型通過使用水平、垂直和旋轉彈簧來考慮水平土抗力、樁側摩阻力和端阻力對剛性樁的水平承載特性的影響。Allotey[2]開發了一種考慮摩阻力效應的有限元模型，研究了在水平循環荷載作用下側摩阻力對樁的動力響應的影響。張小玲等[3]基于圓孔擴孔理論建立了考慮樁側摩阻力影響的樁身撓曲微分方程。Niraula[4]根據樁單元的力矩平衡條件，將樁側摩阻力形成的附加彎矩耦合進土抗力的求解微分方程，并開展嵌巖樁的模型試驗來驗證方程的正確性。上述研究均假定豎向摩阻力沿著半圓周均勻分布，而實際情況中摩阻力在水平加載方向的兩側達到最小值，上述研究高估了樁身豎向摩阻力對單樁水平響應的影響。

有學者從土應力-應變曲線與t-z曲線之間存在比例關系的角度出發，建立樁身附加抗力矩-樁截面轉角(Ms-θ)曲線與土剪應力-剪應變曲線之間的聯系。例如Ashour 等[5]根據現有黏性土中的應力-應變關系推導出附加彎矩的理論公式，結合應變楔模型對彈性地基梁進行水平受力分析，結果表明：樁身摩阻力能夠顯著增加樁頂剛度。Fu 等[6]則使用NGI-ADP 模型得到土單元的應力-應變曲線，根據比例因子換算出p-y曲線和Ms-θ 曲線，采用一維模型與有限元模擬結果進行對比分析。上述研究均適用于黏性土，且作為輸入條件的應力-應變曲線基于特定本構模型的計算結果，不利于工程應用。

Zhang 等[7]同樣提出了將土的應力-應變響應與樁端剪力-位移響應聯系起來的模型，研究并分析了樁端抗力矩對于荷載響應的影響，認為在大多數情況下樁端剪力和抗力矩對水平位移的影響較小。翟恩地等[8]基于荷載-位移曲線建立了針對鋼管樁的樁端水平剪力和樁端抗力矩的有限元公式，但未考慮靜止狀態下的樁端豎向應力對樁端樁-土界面接觸狀態的影響。竺明星等[9]對水平力作用下的樁端豎向應力作用機理進行了研究，竺明星等[9]認為樁端豎向壓力由靜止時的豎向應力和樁端截面轉動引起的附加應力兩部分組成，當樁端抬起一側的卸載應力大于靜止豎向應力時會發生樁-土界面脫開現象。

本文以剛性單樁基礎為研究對象，采用現有的τ-s曲線模型，極限摩阻力考慮了樁側土壓力引起的增強效應，推導出適用于砂土和黏性土的樁身抗力矩的理論計算公式；樁端附加應力采用雙曲線模型計算，結合樁端截面轉動過程中的樁-土界面脫開效應，建立了樁端水平剪力和樁端抗力矩的離散數值計算模型。基于四彈簧地基梁模型，通過有限元方法分析了剛性樁在水平荷載作用下的響應，并與實測結果進行對比，驗證了本文方法的有效性。

1 基本設定與分析模型

如圖1 所示，樁基礎在水平荷載作用下，樁截面的轉動會在樁身表面產生豎向摩阻力τs，由此形成對樁中性軸的附加抗力矩。同時在樁端處，樁端豎向土壓力qb會形成抗力矩，樁端水平位移也會產生水平阻力τb。許多研究結果[6-12]表明：對于短粗剛性樁，樁身抗力矩和樁端阻力對樁水平位移和水平承載力的影響不容忽視，因此本文的研究對象為大直徑剛性樁基礎。當L/T＜2.5 時，單樁可被判定為剛性樁[13]，其中L為樁埋深長度，T按如下公式計算：

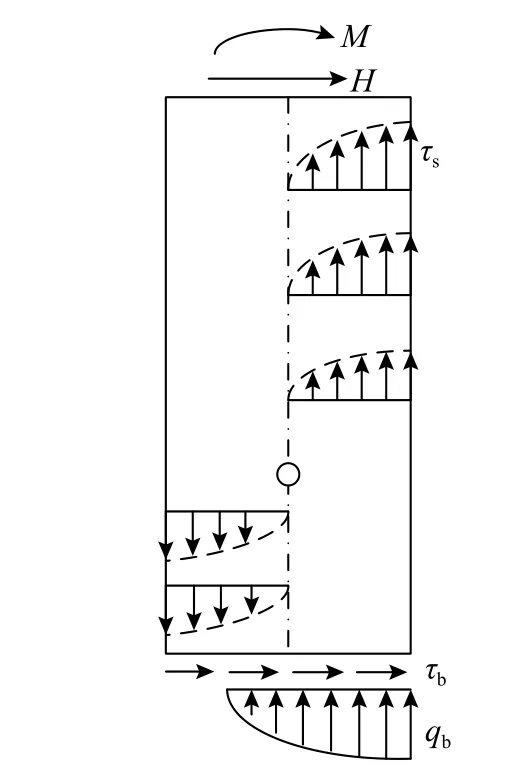
圖1 附加抗力示意圖Fig. 1 Schematic diagram of additional resistance

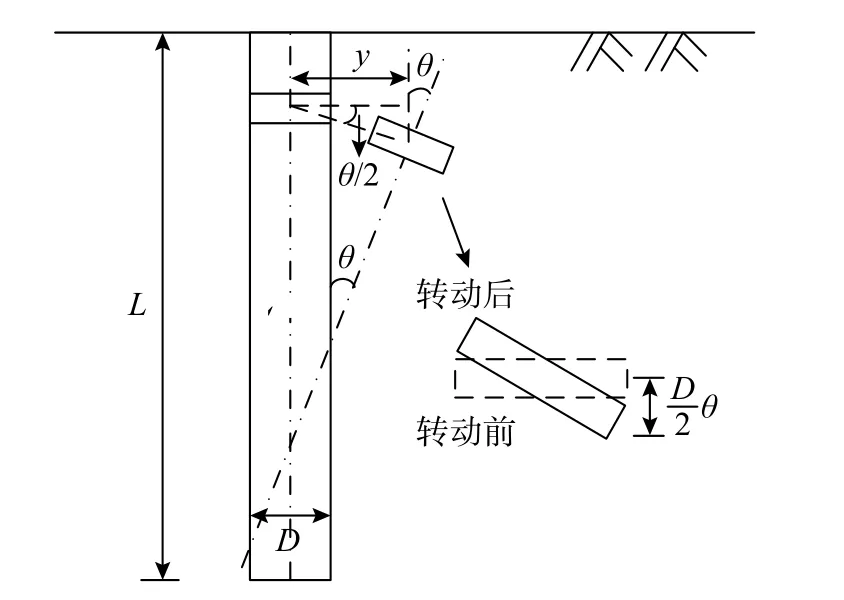
圖2 剛性樁水平位移模式圖(引自Ashour 等[5])Fig. 2 Horizontal displacement model diagram of rigid pile(Cited from Ashour et al[5])

本文采用的模型為四彈簧Winkler 彈性地基梁，如圖3 所示。此模型將樁側土離散為一系列水平和旋轉彈簧。在樁身節點處，水平彈簧定義橫向土抗力p與水平位移y之間的關系，旋轉彈簧定義了樁身抗力矩Ms與樁截面轉角之間的關系；在樁端節點處，水平彈簧代表了樁端剪力Fb與樁端水平位移yb之間的關系，旋轉彈簧代表了樁端抗力矩Mb與樁端截面轉角θb之間的關系。

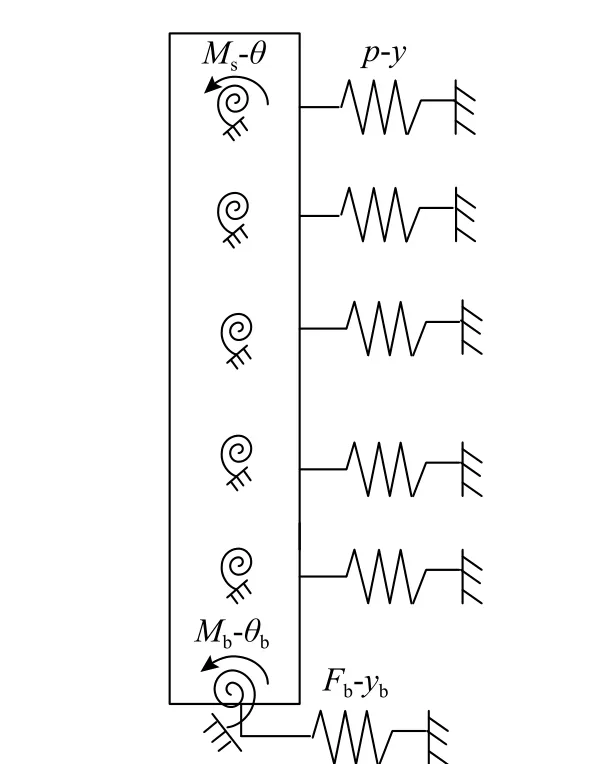
圖3 四彈簧Winkler 地基梁模型Fig. 3 Model of four-spring Winkler foundation beam

2 樁身抗力矩推導

樁側摩阻力發揮與樁土相對位移s有關。樁截面的水平位移和樁截面轉動變形共同引起了樁土相對位移，如圖4 所示，沿樁截面圓周各點的豎向相對位移s為：

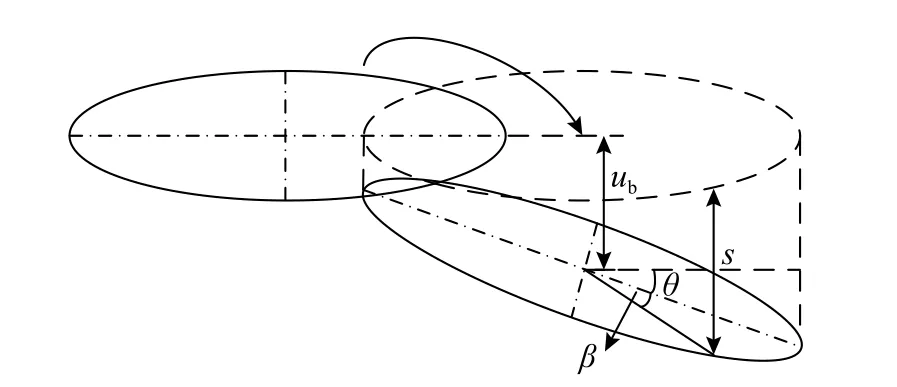
圖4 樁截面豎向位移示意圖Fig. 4 Schematic diagram of pile section vertical displacement

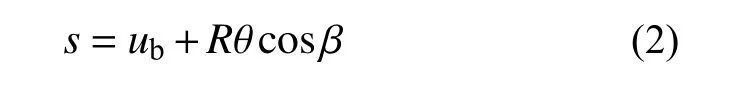
式中：ub為樁軸心處的豎向位移，約為0.5yθ；θ 為樁截面轉角，式(2)第二項是指樁截面轉動的豎向位移，其中β 為計算節點與加載方向的夾角。兩項的比值為0.5y/(Rcosβ)，當β=0 時，比值達到最大值。在y/R的值小于10%的情況下，ub與式(2)第二項的比值不超過5%。因此，本文在計算樁截面各點豎向位移時忽略軸心處的豎向位移ub。式(2)因此變為：

已知樁截面各點豎向位移s，則需要根據摩阻力-位移(τ-s)曲線確定摩阻力τ。鑒于τ-s曲線類型眾多，所以本文依據API 規范[14]提供的τ-s曲線模型，分別對砂土和黏性土中樁身的抗力矩公式進行了推導。

2.1 基于API 砂土摩阻力模型的單位長度樁身抗力矩

API 規范提供的砂土τ-s模型如圖5 虛線所示。

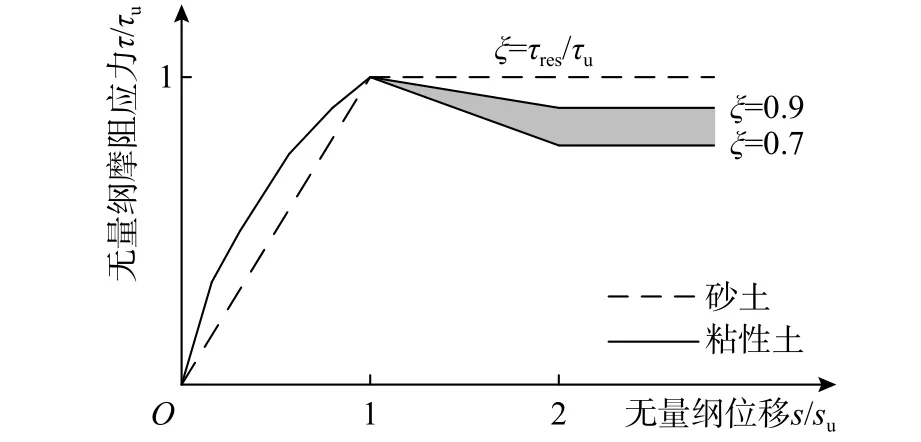
圖5 API 規范[14]摩阻力-位移模型Fig. 5 Model for shaft resistance-displacement of API code[14]

砂土中臨界相對位移su采用API 規范推薦值2.54 mm。極限摩阻力τu則采用庫侖-摩擦定律計算：

式中：σn/kPa 為徑向土壓力；δ 為樁-土界面摩擦角。

眾多試驗數據表明：徑向土壓力沿樁周近似呈橢圓形分布規律，如圖6 所示。Prasad 等[15]利用土壓力傳感器測量了在水平荷載作用下的徑向土壓力分布。Lin 等[16]利用觸覺壓力傳感器測量了荷載變化過程中鋼管樁徑向土壓力的變化趨勢。Liu等[17]同樣利用觸覺壓力傳感器測量了水平位移過程中PVC 管樁的徑向土壓力分布數據。江杰等[18]根據樁周被動測徑向土壓力與徑向位移的關系推導了實際分布形式的樁周土壓力分布計算公式。本文根據文獻[15 - 18]的樁周土壓力測試數據進行擬合，得出以下擬合函數：

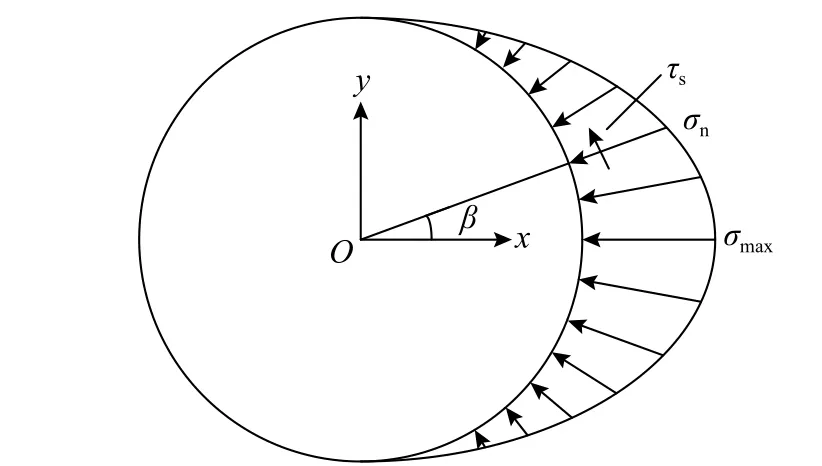
圖6 樁周應力分布示意圖Fig. 6 Diagram of stress distribution around pile

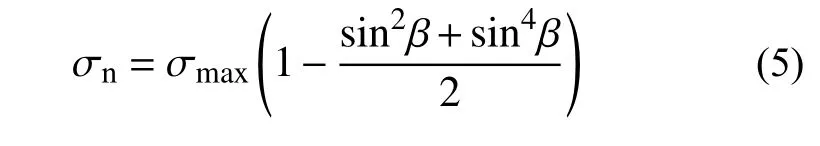
式中： σmax/kPa 為某深度處加載方向最大土壓力；σn/kPa 為夾角β 處的徑向土壓力。

圖7 展示了不同樁頂水平力作用下徑向土壓力的實測值與擬合函數的對比情況，實測數據來自于Lin 等[16]的模型樁試驗。如圖7 所示擬合函數值與實測值較為貼合，證明了擬合函數能較好地預測徑向土壓力沿樁截面的分布規律，可用于樁身極限摩阻力τu的計算。

圖7 徑向土壓力對比圖Fig. 7 Comparison diagram of radial soil pressure

由式(3)可知，樁截面最大相對位移smax=Rθ，發生在最大徑向土壓力σmax處。根據砂土τ-s曲線模型，豎向位移達到臨界位移后，摩阻力等于極限摩阻力τu并且保持不變。本文根據最大相對位移smax與臨界位移su之比分成兩種情況計算樁身單位長度抗力矩，并考慮徑向土壓力的非均勻分布，建立了如圖8 所示樁截面離散示意圖，在此基礎上推導了樁身抗力矩的理論積分公式，采用復化Simpson 積分方法求得樁身抗力矩的數值解。

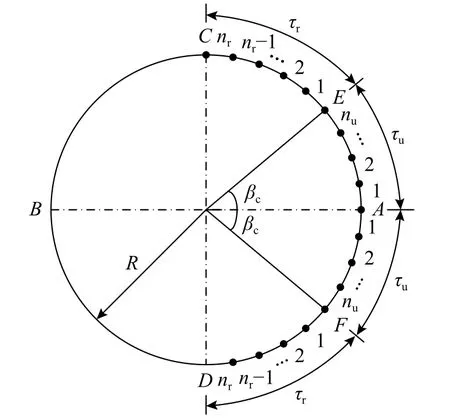
圖8 樁身截面離散示意圖Fig. 8 Discrete diagram of pile section

當smax/su≤1 時，樁側摩阻力為τr，隨著相對位移增長而線性增長，全截面均未達到極限摩阻力τu。將單位長度圓弧內的摩阻力對軸線的力矩沿圓周進行積分，得到單位長度樁身抗力矩Ms/(N·m/m)：

Smith[19]提出水平土抗力p由法向土抗力Fn和沿著樁截面分布的水平摩阻力Fs兩部分組成，基于式(5)所示的徑向土壓力分布形式，分別得到法向土抗力Fn和水平摩阻力Fs的計算公式：

當smax/su＞1 時，如圖8 所示，樁截面圓周上某一點的豎向位移Rθcosβ=su時，樁側摩阻力達到極限摩阻力，此點與原點的連線與OA軸線的夾角為βc，當夾角小于βc時，豎向位移超過su，樁側摩阻力為極限摩阻力；當夾角大于βc時，樁側摩阻力隨著豎向位移線性增加。因此樁身抗力矩Ms分為兩部分計算：

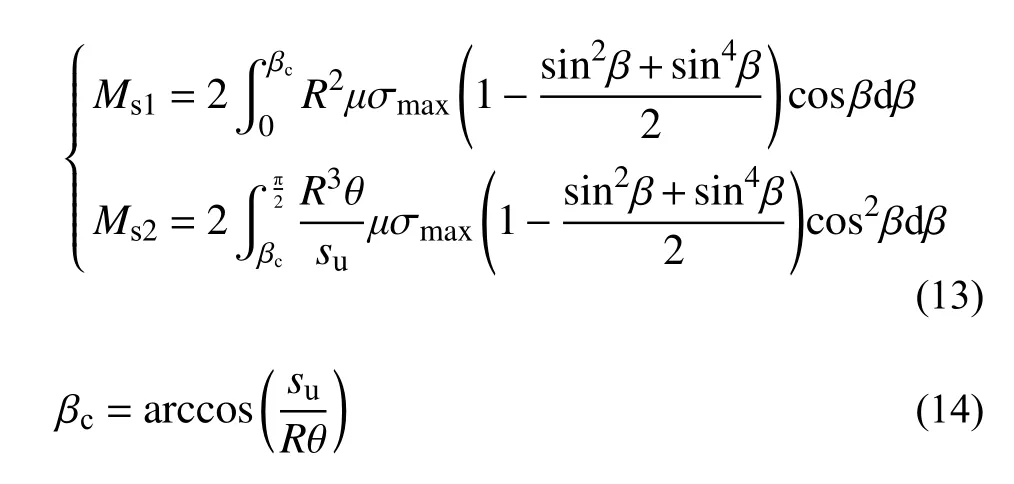
σmax同樣用式(10)進行替代，式(13)轉變為：

2.2 基于API 黏性土摩阻力模型的單位長度樁身抗力矩

API 規范[14]提供的黏性土τ-s模型如圖5 實線所示。此模型為分段軟化模型，當豎向相對位移超過su后，樁側摩阻力隨著相對位移增加而減少，在2su處達到殘余摩阻力值τres。τres與τu的比值在0.7～0.9。類似于砂土τ-s模型的計算方法，本文根據smax/su分為三段計算單位長度樁身抗力矩Ms。

當smax/su≤1 時，API 砂 土τ-s模 型 中s/su與τ/τu之間是線性關系，而對于黏性土則是非線性，對其進行擬合得到如下公式：

對于臨界位移su，API 規范建議取0.01D，Reese[20]的實驗結果表明黏土的su在0.005D～0.02D。對于極限摩阻力τu，Ashour 等[21]建議采用不排水抗剪強度值。

3 樁端抗力矩推導

3.1 樁端抗力矩離散數值解

Allotey 等[22]在計算剛性基礎基底抗力矩時假定基底截面圍繞形心軸旋轉。如圖9 所示，在小角度樁端截面轉角的情況下，樁端附加豎向應力未超過靜止狀態時的樁端豎向有效應力。隨著轉角逐漸增大，附加豎向應力超過靜止樁端豎向應力，被動土壓力一側的樁端截面與土脫開，另一側樁端附加應力接近屈服應力狀態。本文基于上述計算原理建立了如圖10 所示的樁端抗力矩的離散數值計算示意圖。

如圖10 所示，將圓弧AC和圓弧BC等分nb份，第i段圓弧中點與原點的連線與軸線AB的夾角βi=(i-1)π/(4nb)。

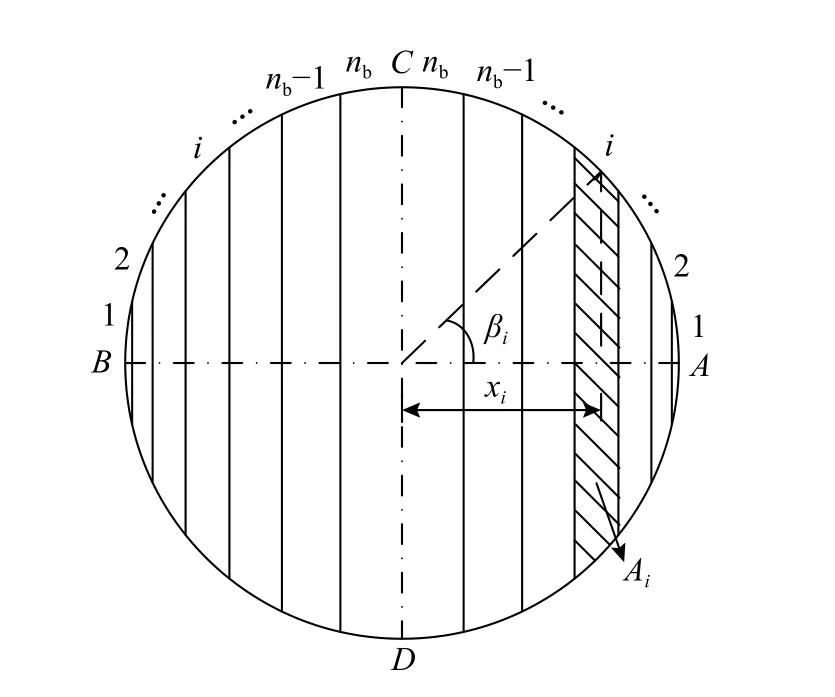
圖10 樁端截面離散示意圖Fig. 10 Discrete diagram of pile tip section

式中：zi為第i段條形豎向位移，zi=xisinθb，xi=Rcosβi，θb為樁端截面轉角；kb/(kN/m3)為曲線初始剛度，Randolph 等[24]建議取kb=4G/(πR(1-ν))，G/MPa 為樁端土剪切模量，ν為土泊松比；qu/kPa為極限端阻力，可選取樁-土界面摩擦角和不排水抗剪強度等參數，根據規范推薦方法進行計算，也可以采用Almeida 等[25]推薦的根據CPTU 測量數據計算極限端阻力的方法，如下列公式所示：

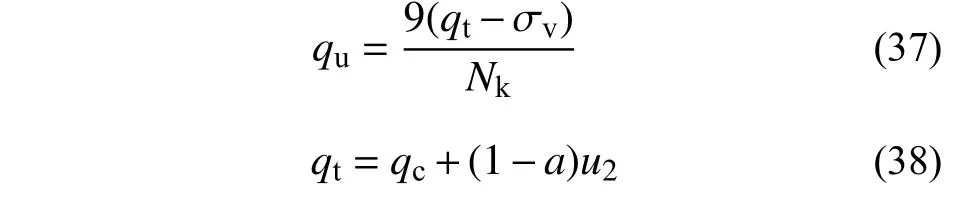
式中：qc/MPa 為錐尖阻力；u2/kPa 為錐尖處測得的孔隙水壓力；σν/kPa 為上覆土有效壓力；Nk為錐尖系數，一般為10～30；a為錐尖面積比，a=0.8。

3.2 樁端抗力矩簡化公式解

王伯惠等[26]基于樁端阻力q與樁端位移z之間呈線性關系的假設，得出樁端抗力矩Mb的理論公式解：

式中：αb為基底土體有效應力與極限端阻力之比，αb=qo/qu，kb和qu所代表意義同式(36)。

4 樁端水平剪力推導

現有的樁端水平剪力計算方法主要基于黏性土層中樁端水平剪力-水平位移(Fb-yb)曲線與樁端土應力-應變(τb-γb)曲線兩者之間的聯系，但缺少砂土層中計算樁端水平剪力的方法。竺明星等[27]提出了線彈性-塑性Fb-yb計算模型，計算參數均取自常見的巖土物理參數，方便于實際應用。由于樁端處樁與土之間的相互作用類似于直剪試驗，故本文采用API 規范摩阻力位移(τ-s)模型(如圖5 所示)計算樁端水平剪力。

砂土中樁端水平剪應力-水平位移(τb-yb)模型為：

式中：η=yb/ybu；ξ=τres/τu，在0.7～0.9；ybu取0.01D；cu為不排水抗剪強度。

為了證明API 黏性土τb-yb曲線模型的有效性，本文與Ashour 等[5]和Fu 等[6]的τb-yb曲線模型進行對比，計算所需參數為：樁直徑D=2 m，不排水抗剪強度cu=150 kPa，ε50=0.52%，破壞時的塑性應變為8%，土剪切模量Gmax與cu的比值為200，臨界位移su=0.01D，對比結果如圖11 所示。

由圖11 可知，當樁端水平位移小于su時，API規范[14]的τb-yb曲線與Fu 等[6]方法計算的τb-yb曲線比較貼近，由于考慮了摩阻力的軟化現象，因此當達到臨界位移后，API 的樁端剪應力會有所折減；在剛開始時，Ashour 等[5]與API[14]和Fu 等[6]的結果相差較多，但隨著水平位移逐漸增大，樁端剪應力逐漸接近于不排水抗剪強度。

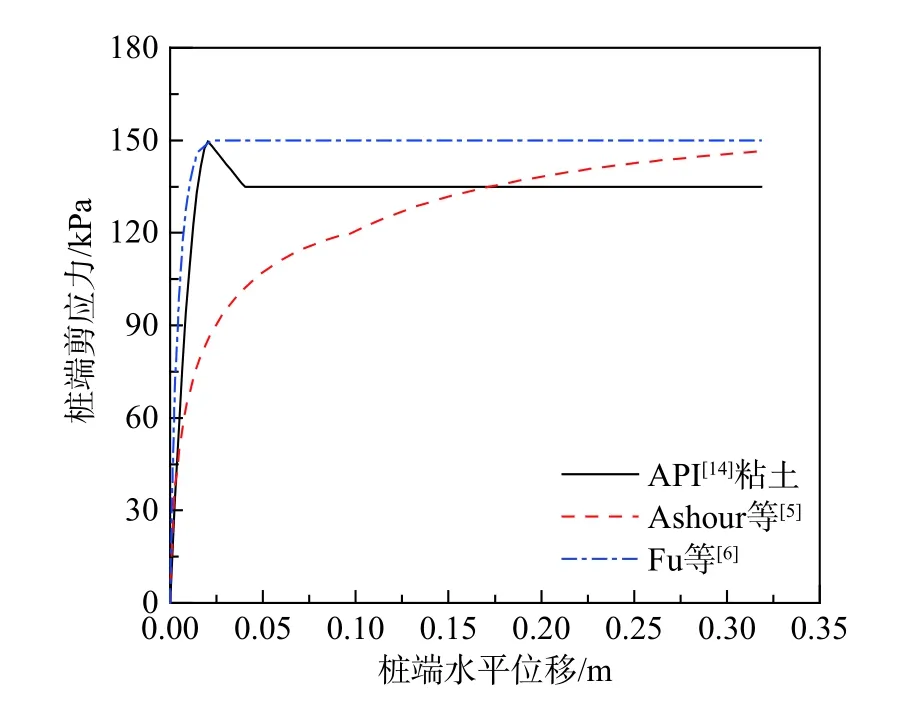
圖11 樁端剪應力-水平位移曲線對比圖Fig. 11 Comparison diagram of curves of pile tip shear stress-horizontal displacement

黏性土中樁端水平剪力Fb為：

式中，Ab為樁端樁-土界面接觸面積，考慮了樁-土界面脫開效應。

5 有限元計算方法

本文采用一維Winkler 彈性地基梁模型，將樁等分成n段，并在各分段節點上施加一個水平彈簧和一個旋轉彈簧，以反映土對樁的水平土抗力和附加抗力矩作用。由于忽略了樁軸線處的豎向位移，每個節點只有兩個自由度：水平位移u和轉角θ。總體平衡方程為：

式中：R2i-1/kN 為第i個節點上的水平反力；pi/(kN/m)為單位長度水平土抗力；kl,i/(kN/m2)為p-y曲線割線剛度；yi為第i個節點的水平位移；R2i/(kN·m)為第i個節點上的反力彎矩；Ms/(kN·m/m)為單位長度樁身抗力矩；kr,i/(kN·m/m)為Ms-θ 曲線割線剛度；θi為第i個節點的轉角。當i=1 或n+1 時，dL=L/(2n)，其他節點dL=L/n。

根據式(49)，R可改寫為如下形式：

本文利用MATLAB 編制基于上述有限元公式的單樁水平受力分析程序，計算步驟說明如下：

1) 輸入計算所需的參數，劃分節點和單元，計算樁總剛度矩陣Kp，計算每個節點的p-y曲線和Ms-θ 曲線，以及樁端節點的Mb-θb曲線和Fb-yb曲線。

2) 計算各個節點處的p-y曲線的初始剛度kl,ini，生成對角矩陣Ks，其中奇數行的對角元素為kl,inidL，偶數行對角元素為0。

3) 根據式(51)求得節點位移向量a。

4) 根據節點水平位移和轉角，求得每個節點的p-y曲線割線剛度kl,i和Ms-θ 曲線割線剛度kr,i，重新生成矩陣Ks。如果考慮樁端阻力，則需在矩陣Ks相應對角元素處加上Mb-θb曲線割線剛度kl,b和Fb-yb曲線割線剛度kr,b。

da=K-1(F-Kam)

5) ，上標m表示第m次迭代，若||da||/||am|| ＜ε=1×10-4，則滿足收斂條件進行下一步。若不收斂，am+1=am+ da，返回步驟4)。

6) 根據節點位移求解樁身內力。

6 算例驗證

6.1 算例1

Bhushan 等[28]在開展了砂土場地鉆孔灌注樁的多組水平加載試驗，其中在場地C 中安裝了7#試樁，樁直樁為1.22 m，樁長5.5 m，樁的埋置深度為5.5 m，樁的彈性模量為32.4 GPa，L/T=2.4＜2.5，屬于剛性樁。試驗加載點位于泥面處，每級水平荷載增量為127 kN，直到最大荷載890 kN 終止加載。場地C 一共包含兩層土，第一層土厚度為1.8 m，內摩擦角為36°；第二層土厚度為3.7 m，內摩擦角為42°，兩層土的重度都為16.5 kN/m3。樁-土界面摩擦角為內摩擦角的0.6 倍，樁端土的剪切模量為25.4 MPa，極限端阻力為9 MPa。砂土的p-y曲線根據API 規范計算。基于本文提出的計算方法編制程序計算樁身位移，并與實測值進行對比。圖12 為7#試樁泥面水平位移的結果對比圖。

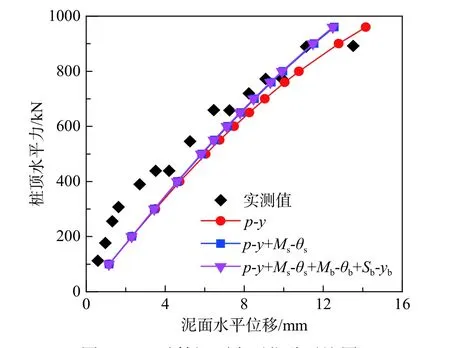
圖12 7#試樁泥面水平位移對比圖Fig. 12 Comparison diagram of horizontal displacement of test pile 7 on mudline

由圖12 可知，只考慮p-y曲線時的泥面水平位移計算值小于實測值，采用四彈簧模型的計算結果小于p-y曲線法，與實測值更為吻合。在水平荷載較小的情況下，只考慮p-y曲線時與四種彈簧曲線都考慮時的泥面水平位移較為接近；隨著荷載的逐漸增大，兩種情況下的泥面位移差值逐漸增大，采用四彈簧模型的計算結果更接近于實測值。從圖12 可以看出，樁端水平剪力和抗力矩對水平位移的影響較小，這是由于此時樁端位移較小，樁端水平剪力并未充分發揮作用。

6.2 算例2

Klinkvort 等[29]利用離心機試驗模擬了砂土中實心鋼樁在水平荷載作用下的響應。其中模型樁T5 的樁直徑為40 mm，長徑比為6，L/T=1.16＜2.5，屬于剛性樁，離心加速度為77.7g，原型樁的直徑為5 m，樁埋深長度為30 m，泥面以上樁長75 m，水平荷載加載點位于樁頂，當水平位移明顯增大時終止加載。砂土相對密度為90 %，有效重度為16.8 kN/m3，內摩擦角φ為40°，樁-土界面摩擦角δ = 0.7φ，樁端土剪切模量為50.4 MPa，樁端極限端阻力為7.7 MPa。

由圖13 可知，只考慮p-y曲線時的樁頂水平位移明顯小于實測值。當樁頂荷載小于30 000 kN時，考慮四彈簧曲線的計算結果與p-y曲線法較為接近；樁頂荷載超過30 000 kN 時, 采用四彈簧模型計算的結果更接近于實測值，而p-y曲線法計算的樁頂水平位移明顯偏大，荷載位移曲線也較早進入塑性階段。采用四彈簧模型計算的極限水平承載力為54 000 kN，而采用p-y曲線法計算的極限水平承載力為46 000 kN，說明四彈簧模型能較大提高樁基的水平承載力。水平荷載較小時樁端水平阻力和抗力矩對于樁基水平承載力的影響并不明顯，荷載位移曲線進入塑性階段后，此時樁端剪力與樁端抗力矩開始發揮作用，使得樁基礎的水平承載能力有所提高。

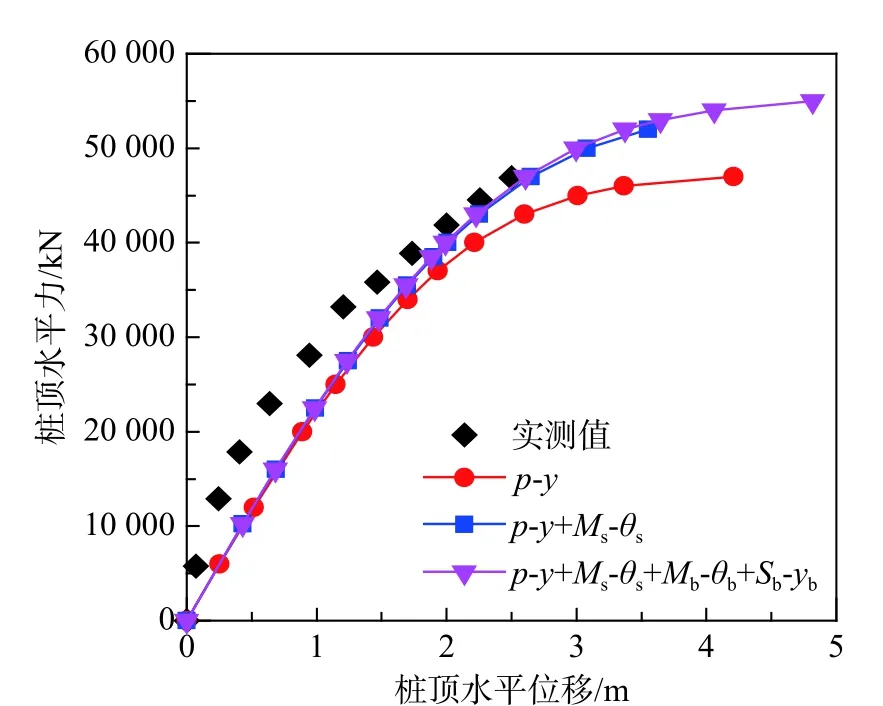
圖13 樁頂水平力-位移曲線對比圖Fig. 13 Comparison diagram of pile head forcedisplacement curves

6.3 算例3

聯合行業項目PISA[30]中在Cowden 的硬黏土場地上對鋼管樁基礎進行了水平加載試驗。其中試樁CL2 的直徑D=2 m，壁厚t=25 mm，樁長20.5 m，其中泥面以上長度為10 m，埋置深度L=10.5 m，長徑比為5.25，加載位置位于樁頂，當樁頂水平位移急劇增加，位移速率明顯增大時終止水平加載。場地土體參數如表1 所示，土層有效重度為11.2 kN/m3。樁端土剪切模量為28.2 MPa，樁端處的錐尖阻力qc=2.6 MPa，孔隙水壓力u2=250 kPa，根據式(37)～式(38)計算的極限端阻力qu=1.42 MPa。黏土的p-y曲線根據API 規范計算。

試樁CL2 泥面水平位移的對比結果如圖14 所示。采用四彈簧模型計算的泥面位移更接近實測值，驗證了本文提出的黏性土中樁身抗力矩和樁端剪力和彎矩模型的正確性。而p-y曲線法的計算結果與實測值相比差距較大，三維有限元軟件計算結果顯示API 的p-y曲線模型嚴重低估了初始剛度和極限土抗力，因此在分析樁的水平受力響應時，p-y曲線模型仍是主要因素。

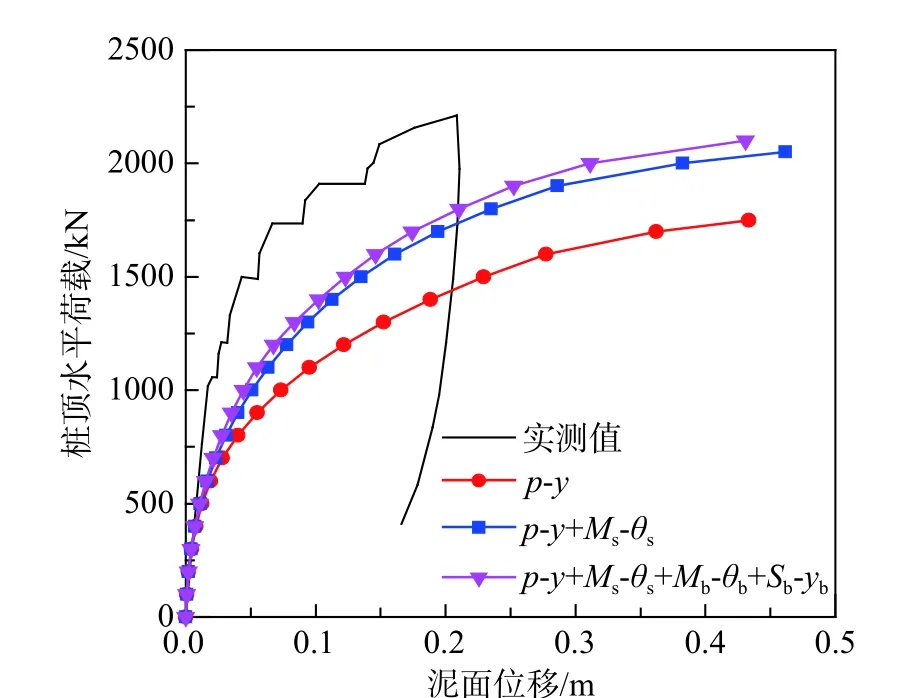
圖14 試樁CL2 荷載位移曲線Fig. 14 Curves of load-displacement of test pile CL2

圖15 展示了泥面位移為20.8 mm 時采用p-y曲線法和四彈簧模型法計算的樁身彎矩與實測值的對比情況。由于泥面位移相同時，三種彈簧施加模式下的樁頂荷載不同，因此計算得到的樁身彎矩會有顯著區別。深度小于7.5 m 時，p-y曲線法和四彈簧模型法計算的樁身彎矩明顯小于實測值，p-y曲線法計算的樁身彎矩最小，分別施加Ms-θ、Mb-θb和Fb-yb彈 簧 后，樁 身 彎 矩 逐 漸 增加，四彈簧模型法的計算結果更接近于實測值。

由圖14 和圖15 可以看出，在考慮Ms、Fb和Mb等附加抗力影響后，樁身響應計算值與實測值仍有一定差距，這是由于API 規范采用的Matlock黏土p-y曲線的極限土抗力較低導致的。 Zhang等[31]對比了Matlock[32]、Reese 等[20]、Broms[33]和Randolph 等[24]學者關于黏性土極限土抗力的計算結果以及Hamilton 等[34]的試驗數據，發現基于Matlock 方法計算的極限土抗力在眾多方法中處于最小值，且與實測數據相比也相差較多。李洪江等[35]基于Vesic 圓孔擴張理論推導了黏性土的p-y曲線模型，通過將計算的p-y曲線與Matlock 方法和實測值三者進行對比，同樣發現基于Matlock方法計算的極限土抗力較低。因此在進行單樁水平受力分析時應選取更先進合理的p-y曲線模型。

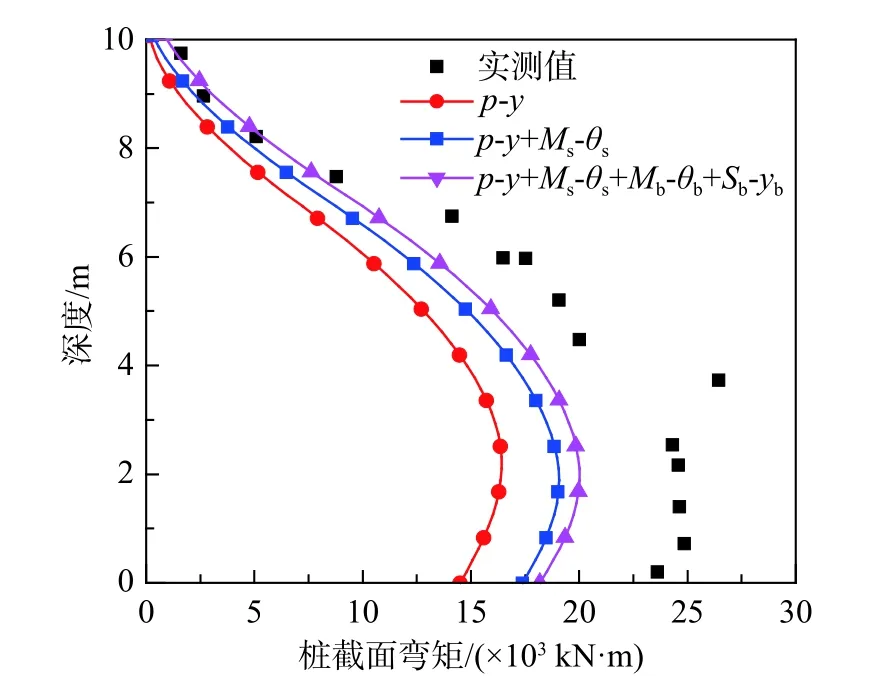
圖15 試樁CL2 樁身彎矩分布曲線Fig. 15 Bending moment distribution curve of test pile CL2

7 水平承載力分析

大直徑單樁在水平荷載作用下，當泥面處水平位移達到0.1D時，此時的樁頂荷載定義為樁的水平承載力。為探究四種土反力(水平土抗力p、樁身抗力矩Ms、樁端剪力Fb和樁端抗力矩Mb)對于樁基水平承載力的影響，通過將p-y、Ms-θ、Fb-yb和Mb-θb彈簧依次加入到模型中，每加入一種土反力彈簧計算一次水平承載力Fu,i，當所有土反力彈簧施加完畢時得到總水平承載力Fu,sum，則每種土反力彈簧在總水平承載力中的占比為ΔFu(%)=(Fu,i-Fu,i-1) /Fu,sum×100%。本文分別在砂土地基和黏性土地基中開展水平承載力計算，探究四種土反力分別在不同樁直徑和不同長徑比情況下在總水平承載力中的占比的變化趨勢。

7.1 砂土地基參數分析

Bhushan 等[28]在砂土地基場地B 中進行了多組鉆孔灌注樁加載試驗，試驗樁彈性模量為32.4 GPa，加載點設置在泥面處。試驗場地有兩層土，第一層土厚度為0.9 m，內摩擦角為36°；第二層土厚度為14 m，內摩擦角為42°，土的有效重度為16.5 kN/m3。基于此場地參數開展水平承載力計算，樁直徑對四種土反力在總水平承載力占比的影響如圖16 所示，長徑比L/D對四種土反力在總水平承載力占比的影響如圖17 所示。

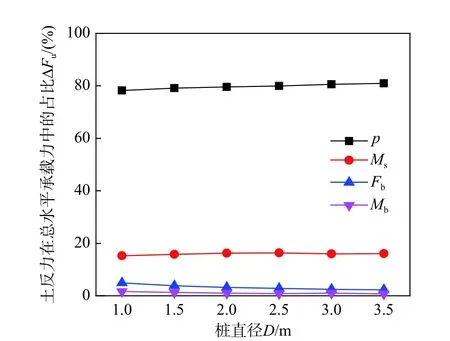
圖16 不同樁直徑下土反力對總水平承載力的影響Fig. 16 Influence of soil reaction on total horizontal bearing capacity under different pile diameters

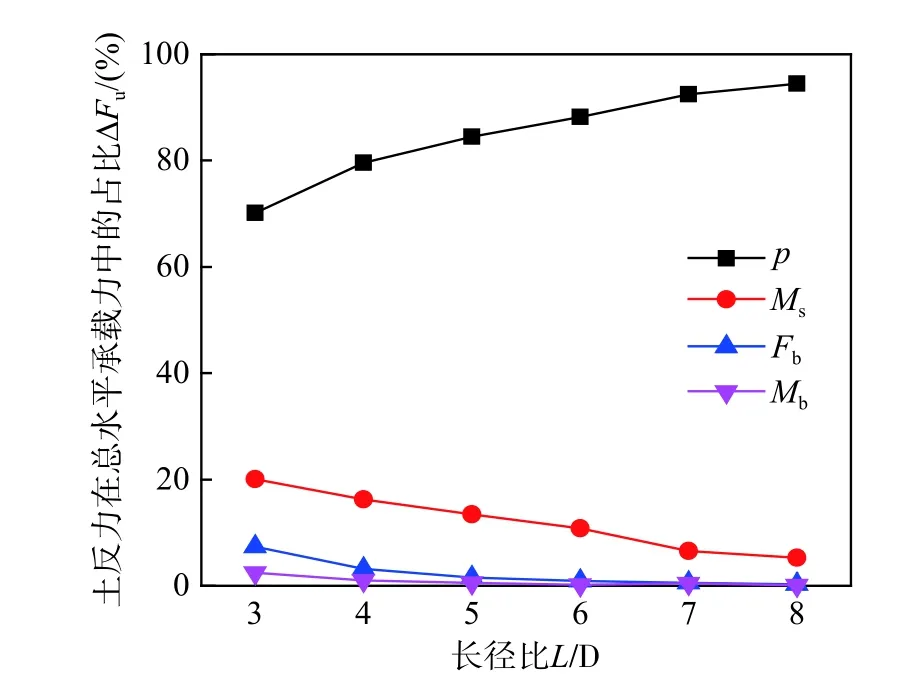
圖17 不同長徑比下四種抗力對總水平承載力的影響Fig. 17 Influence of four resistances on total horizontal bearing capacity under different ratios of pile length to diameter

圖16 中樁長徑比L/D=4，并保持不變，樁直徑D從1 m 增加到3.5 m。由圖16 可知四種土反力對于水平承載力的影響沒有顯著變化。水平土抗力p提供了主要的承載力作用，并且隨著樁直徑增加，p在總水平承載力中的占比略有上升。Ms、Fb和Mb相比于p一共提升了約25 %的水平承載力，三者之中Ms在總水平承載力的占比最大，約為16%；Mb的占比最小，約為1.1%；隨著樁直徑的增加，Fb對樁的水平承載力的影響略有下降。

圖17 中樁直徑D=2 m，并保持不變，長徑比L/D從3 增大到8。由圖17 可知四種土反力對于水平承載力的貢獻均發生了顯著變化。p在總水平承載力中的占比從70 %增大到94 %，說明對于長徑比較大的半剛性樁或柔性樁，采用p-y曲線法與四彈簧模型法計算的水平承載力差異較小。隨著L/D的增加，Ms、Fb和Mb在總水平承載力的占比逐漸下降。其中Ms在總水平承載力的占比從20 %下降到5.3 %，下降幅度最為顯著；當L/D大于6 時，Fb和Mb在總水平承載力中的占比接近于0，這是由于隨著長徑比逐漸增大，樁身變形由剛性轉動轉變為柔性變形，樁端水平位移和轉角較小，由此產生的樁端剪力和樁端抗力矩也較小，因此無法對樁水平承載力產生影響。

Murphy 等[36]利用PLAXIS 軟件并且采用硬化土本構模型模擬了砂土土層中單樁在水平靜力作用下的響應，其中樁直徑為0.51 m，內摩擦角平均值為45°。計算結果顯示：當L/D由3 增大到6時，p-y彈簧對水平承載力的貢獻由74 %增大到88 %，Ms-θ 彈簧對水平承載力的貢獻由13 %減小到5 %，Fb-yb彈簧對水平承載力的貢獻由8 % 減小到5.5 %，這與本文模型分析得到的四種土反力對水平承載力的貢獻隨長徑比變化規律較為接近，驗證了本文模型的有效性。

7.2 黏性土地基參數分析

黏性土地基中參數分析沿用了算例3 中PISA項目硬黏土場地的土層參數，假設水平加載點位于泥面以上8 m 處。黏性土地基中樁直徑對四種土反力在總水平承載力中占比的影響如圖18 所示，長徑比L/D對四種土反力在總水平承載力中的占比的影響如圖19 所示。

圖18 不同樁直徑下四種抗力對總水平承載力的影響Fig. 18 Influence of four resistances on total horizontal bearing capacity under different pile diameters

圖18 中樁的長徑比L/D=4，樁直徑由2 m 增加到8 m。由圖18 可知，黏性土地基中四種土反力在總水平承載力中占比的變化規律類似于砂土地基。p、Ms和Mb在總水平承載力的占比基本保持不變，樁端剪力Fb在總水平承載力中的占比略有下降。

圖19 中樁直徑D=3 m，長徑比L/D從2 增大到7。從圖19 中也觀察到與砂土地基中相似的變化規律，即隨著長徑比逐漸增大，水平土抗力p在總水平承載力中的占比逐漸增加，Ms、Fb和Mb對于總水平承載力的貢獻逐漸減小。

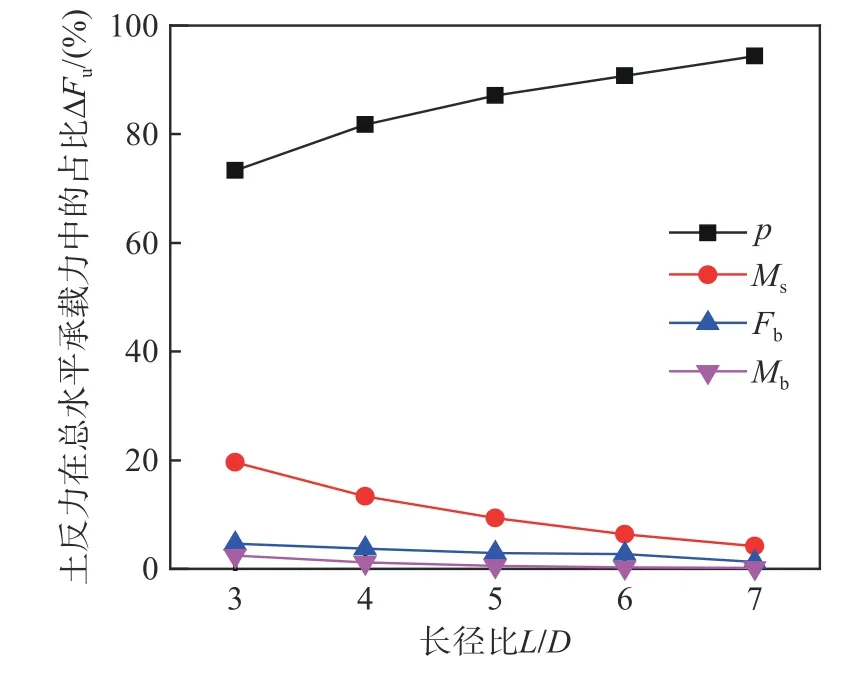
圖19 不同長徑比下四種抗力對總水平承載力的影響Fig. 19 Influence of four resistances on total horizontal bearing capacity under different ratios of pile length to diameter

8 結論

本文基于API 規范推薦的τ-s曲線模型，分別推導了砂土和黏性土中樁身抗力矩的離散數值解和簡化公式解，并根據本文提出的樁端豎向應力計算模型，推導出樁端抗力矩和樁端水平剪力的計算公式。基于Winkler 地基梁模型，采用有限元方法編制成MATLAB 程序，通過對比實測數據驗證了本文模型的有效性。最后通過參數分析研究了樁直徑和長徑比L/D對水平土抗力p、樁身抗力矩Ms、樁端水平剪力Fb和抗力矩Mb在總水平承載力中占比的影響規律。本文得出如下主要結論：

(1) 通過算例驗證，證明了本文提出Ms、Fb和Mb的理論計算公式是可行的。與傳統p-y曲線法相比，本文方法所得計算結果更接近于實測值。

(2) 水平荷載較小時，四彈簧模型法與p-y曲線法計算結果較為接近；隨著荷載逐漸增大，四彈簧模型法計算的樁身位移逐漸小于p-y曲線法的計算結果，同時更接近于實測值。

(3) 在樁的水平承載特性分析中，p-y曲線模型是主要的影響因素。選用更先進合理的p-y曲線模型能夠提升計算結果的有效性。

(4) 隨著樁直徑的增大，p、Ms、Fb和Mb在總水平承載力中的占比并無顯著變化；當長徑比L/D逐漸增大時，水平土抗力p在總水平承載力中的占比逐漸增加，Ms、Fb和Mb在水平承載力中的占比逐漸減小