中職數學中數形結合思想的應用

劉永強

【摘要】數形結合思想是解決數學問題的重要數學思想之一，它“以形助數”，化抽象為直觀，“以數解形”，將“形”的特征用“數”的嚴密性和準確性表示出來。抽象思維與形象思維的結合，實現了優化解題途徑的目的，有效幫助學生理解抽象的數學問題，有助于學生對數學知識獲得過程及理論來源的理解。本文以實際例子論述數形結合思想在中職數學教學中的應用，并給出了數形結合方法的教學建議。

【關鍵詞】中職數學；數形結合思想；應用；建議

【中圖分類號】G718.3【文獻標志碼】A【文章編號】1004—0463（2022）10—0061—04

新《中等職業學校數學課程標準》課程任務指出：“使中等職業學校學生獲得進一步學習和職業發展所必須的數學知識、數學技能、數學方法、數學思想和活動經驗。”數形結合思想是其中重要的數學思想之一，能有效幫助學生理解抽象的數學問題，優化解題途徑。“數”和“形”是數學中兩個最古老、最基本的研究對象，主要研究數字、算術、數量關系等與圖形知識之間的關系，它們相輔相成，緊密結合，在一定條件下又可以相互轉化。我國著名數學家華羅庚曾說過：“數形結合百般好，割裂分家萬事休。”諸多數學研究者和數學教師對這一課題的研究頗多，但其側重點不同。丁杭纓認為：“數形結合既是教師教學的重要目標，也是學生數學學習的目的。”[1]李雪認為：“數形結合的實質是把抽象的代數與形象的圖形結合起來，代數問題與圖形問題彼此轉化。”[2]顧越嶺認為：“考慮問題時數、形兼顧，將其直觀性與抽象性有機結合起來，使我們的認識更加全面、更加深刻。”[3]筆者搜索知網，查閱大量關于數形結合思想的研究資料，發現研究者們的觀點基本一致，認為數形結合就是把代數問題與幾何圖形結合起來，“以形助數，以數解形”，化抽象為具體，達到事半功倍的效果[4]。

絕大多數中等職業學校的學生是中考后分數未能過普高錄取線的考生，他們文化課底子差、基礎弱，尤其在數學學習上困難重重。很多學生在小學階段就落下了數學基礎知識，基本數學概念不清；常用公式、運算法則及性質理解不透，相互混淆；基本運算能力差，有學生甚至連計算2-（-8）這樣簡單的運算都要考慮很長時間，學習上心有余而力不足，嚴重影響了學生學習的積極性。為此，教師改變傳統的數學教學思想和方法，注重數學學科內在的、學科素養——“以形助數，以數解形”，化抽象為直觀，優化解題路徑，激發學生的學習興趣。

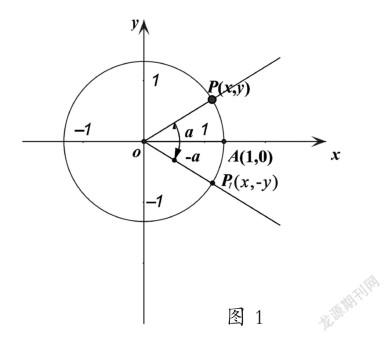
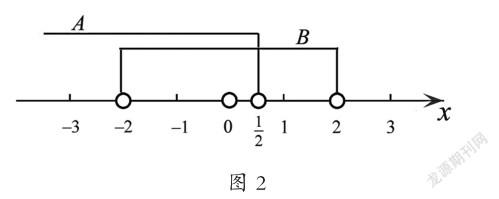
可見，處理集合問題，用數形結合的方法，可以使集合之間的關系及運算直觀化，更容易求解問題的結果。

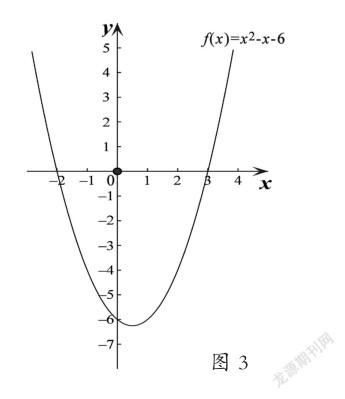
在數學教學中，很多教師受“高考模式”影響，沿用傳統的教學思想，重結果輕過程，學生獲得的數學知識比較死，增加了記憶量，還容易混淆。運用數形結合思想，使學生對數學結論獲得本源性的過程體會，從實質上理解了知識的來龍去脈，化抽象為具體，直觀呈現，降低了學生的理解難度。

3.以數解形，將“形”的特征用“數”的嚴密性和準確性表示出來。“形”雖然在直觀性上有很多優勢，能把抽象的問題形象地表示出來，但在定量上，無論是簡單的還是復雜的圖形，都必須借助于“數”，用“數”精準地描述“形”的特征、數量關系，兩者之間的完美結合，使得數學知識學習不斷向縱深方向發展。例如，函數y=f（x）的圖象如圖4所示，觀察圖形，讓學生把從圖上看到的所有圖形特征說出來。這就需要用數學語言完整地描述圖形特征，匯總如下：

（1）函數y=f（x）的定義域[-3，3]，值域[-1，2]；

（2）當x=-1時，函數有最大值2，當x=2時，函數有最小值-1；

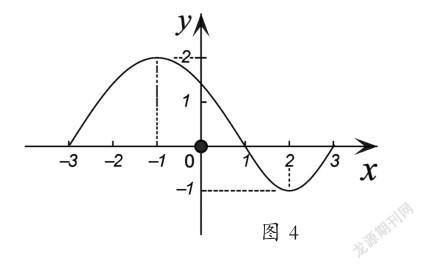
（3）在整個定義域上，函數不具有單調性，但在定義域的某些區間上具有單調性，如在區間[-3，-1]∪[2，3]上函數單調遞增，在區間[-1，2]上單調遞減；

（4）這是一個非奇非偶函數。

用“數”把“形”所表現出的所有特征、性質進行總結，訓練了學生觀察、分析、總結問題的邏輯能力，加深了對函數性質等相關知識的理解。

中職數學教材在編寫上以學生的年齡特點、心理特征及學習基礎為出發點，突出職業性和基礎性，依照“實例”“觀察”“新知識”“知識鞏固”“練習”“現代信息技術應用”“閱讀與欣賞”等板塊組織教學。對學生而言，數學知識的呈現很明確，而數學知識中蘊含的數學思想卻是看不見、摸不到的，這就需要教師在課堂教學中潛移默化地滲透。中職數學教學思想包含很多種，知識化歸、數形結合等數學思想方法之間既密切聯系又各具特色。在運用數形結合思想探究或解決問題時，需要把握以下幾點。

1.概念教學中滲透數形結合思想。數學概念猶如法律條文，其基礎性地位特別高，是數學重要知識點的濃縮。學生對概念的認知過程要經過分析、比較、抽象、提煉、概括和歸納等思維加工，而不是簡單的記憶和理解。實際教學過程中，教師要盡量把抽象的理性知識通過“形”直觀表示，加深學生對概念的理解，從而提升學習效果。如小學的分數概念，初中數學中的絕對值、相反數等概念性知識的講解都可以運用數形結合思想完美闡釋。中職數學基礎模塊上冊第五章學習任意角的概念時，需要大量滲透數形結合思想，使抽象的概念具體化。如理解正負角的概念，從圖5的三個圖形中直觀觀察出它們都是角，記作∠AOB，但意義不同：圖①和圖②是正角，圖③是負角，教師在講述概念時要結合圖形緊扣角是由始邊繞著頂點按照順時針方向還是逆時針方向旋轉形成的這一關鍵點，學生就會心領神會。

2.公式、定理教學中感悟數形結合思想。數學學習中，涉及到的公式和定理很多，也比較抽象，記憶起來比較困難，尤其數學公式容易混淆、記錯。其主要原因在于學生對公式、定理的本源性理解不到位，這就需要教師在講解知識時合理利用數形結合思想，幫助學生從“形”中領悟公式、定理的幾何意義，加深理解，記憶公式、定理。如中職數學誘導公式、直線與圓的方程等數學知識，都可以通過圖形幫助記憶理解。

3.解題方法中突出數形結合思想。只有在解題過程中突出數形結合思想方法，才是最好的運用。雖然數形結合思想方法貫穿于數學學習和研究的始終，但運用于解題方法教學中要注意把握度和適用性原則。中職學生數學底子薄弱，在教學過程中要關注問題中涉及的“數”與潛在的“形”之間是否具有等價性，能否使問題簡單化。

總之，數形結合既是“數”與“形”的等價結合，也是數學思想與數學研究及學習方法的有機結合，在運用過程中要注重由“數”的抽象到“形”的直觀轉化以及由“形”到“數”的精準描述。

[1]丁杭纓.給學生一個立體的“數學”——例談“數形結合”[J].人民教育，2010（07）：39-42.

[2]李雪.初中數學數形結合思想教學研究與案例分析[D].河北：河北師范大學，2014：63.

[3]顧越嶺.數學解題通論[M].桂林：廣西教育出版社，2000：120.

[4]游雪峰.數形結合在中職數學教學中的應用研究[A].教學應用就業，2016.

[5]徐文龍.“數形結合”的認知心理研究[D].桂林：廣西師范大學，2005：06-08.

（本文系2020年度甘肅省“十三五”教育科學規劃一般課題“‘三教’改革背景下中職文化課教學困境及對策研究”的研究成果，課題立項號：GS[2020]GHB3125）

編輯：徐春霞