數形結合思想在高中數學中的應用

張鑫

【摘要】數學是研究空間形式和數量關系的科學，數與形看似是兩個部分的內容，實際上在數學中有著十分密切的聯系.在高中數學的學習中，數形結合思想有助于學生理解數學內容;在高中數學的解題中，很多時候將數與形結合，可以簡化解題過程，開拓學生思路.可見，數形結合思想是十分重要的.本文將簡單闡述數形結合思想的實質和重要作用，然后舉例說明數形結合思想在高中數學中的應用.

【關鍵詞】數與形;數形結合思想;應用

一、數形結合思想的實質

數形結合思想方法的實質是指將抽象的數學語言和直觀圖形結合起來，使抽象思維與形象思維結合起來.通過對圖形的處理發揮直觀對抽象的支柱作用，通過對數與式的轉換，圖形的特征及幾何關系被刻畫得更加精細和準確，這樣就可以使抽象概念和具體形象相互聯系、相互補充、相互轉化.

二、數形結合思想在高中數學中的重要作用

（一）幫助學生理解新知識

在代數課堂的導入中，如果教師用教具或是多媒體展示出一個動態的教學案例，會引起學生興趣、激發學生學習的欲望，可以順其自然地引入一堂課.在高中數學教學中，對于很多知識點，教師直接講解可能不會讓學生理解到關鍵，甚至難以記住，而借助圖形直觀地向學生展示知識點的推理過程，可以促進學生理解知識，加深學生的印象.比如，教師在講余弦定理的時候，可以用平面上的三角形通過向量法進行證明，讓學生對余弦定理的記憶有一個幾何層面的理解，這樣會開闊學生的思維.幾何直觀與代數運算之間的融合，會讓學生感悟數學知識之間的關聯，加強對數學整體性的理解.

（二）為學生解題提供新思路

數學內容本身具有普遍聯系的特點，所以在數學解題中，為了解題方便，代數問題可以轉化為幾何問題來解決，幾何問題可以轉化為代數問題來解決.很多時候代數問題直接推導求解會很麻煩，如果可以用幾何圖形進行解決，那么代數問題會解決得更加容易.比如，在求一元二次不等式的解集時，我們可以畫出對應的二次函數的圖像，觀察圖像與橫軸交點情況，圖像在橫軸上方時，不等式大于零，圖像在橫軸下方時，不等式小于零.

（三）促進學生思維的發展

對于數學中較難理解的概念或者定理，教師若分別從數與形這兩個角度闡述，則可以使學生對這部分知識的理解更為深刻、具體，從而豐富學生頭腦中的認知結構.代數主要運用的是抽象思維，幾何主要運用的是形象思維，而數形結合思想則要求學生的思維在抽象思維與形象思維之間轉換，這一定會促進學生數學思維的發展，并且這種相互轉換的方法也會使學生在生活中受益.在數形轉換的過程中，學生會從一個目標出發，沿著不同的途徑去思考，探求多種答案，這可以發展學生的發散思維.

（四）發展學生數學能力和數學核心素養

數形相輔，借助幾何圖形來幫助學生理解較難理解的數、數量關系，可以最大限度地促進學生數學邏輯思維的發展.這個過程要求學生能將表達空間形狀、大小、位置關系的數學語言與具體的實際特征結合起來，提高學生的快速匹配認知能力與空間想象能力.在數形轉換這個過程中，數形結合思想有助于發展學生的邏輯推理、直觀想象和數學運算的核心素養.

三、數形結合思想在高中數學中的應用

（一）數形結合思想在函數中的應用

數形結合思想在函數中的應用有很多：通過數形結合思想求函數最值問題、通過導數圖像的正負畫出原函數圖像的單調性、結合一元二次函數的圖像可以判斷一元二次方程實根的存在性及實根的個數.下面舉一個分段函數求最值的問題，通過畫函數圖像可以直觀地解決問題.

例1 設函數f（x）=x3-3x，x≤a，-2x，x>a.

（1）若a=0，則f（x）的最大值為;

（2）若f（x）無最大值，則實數a的取值范圍是.

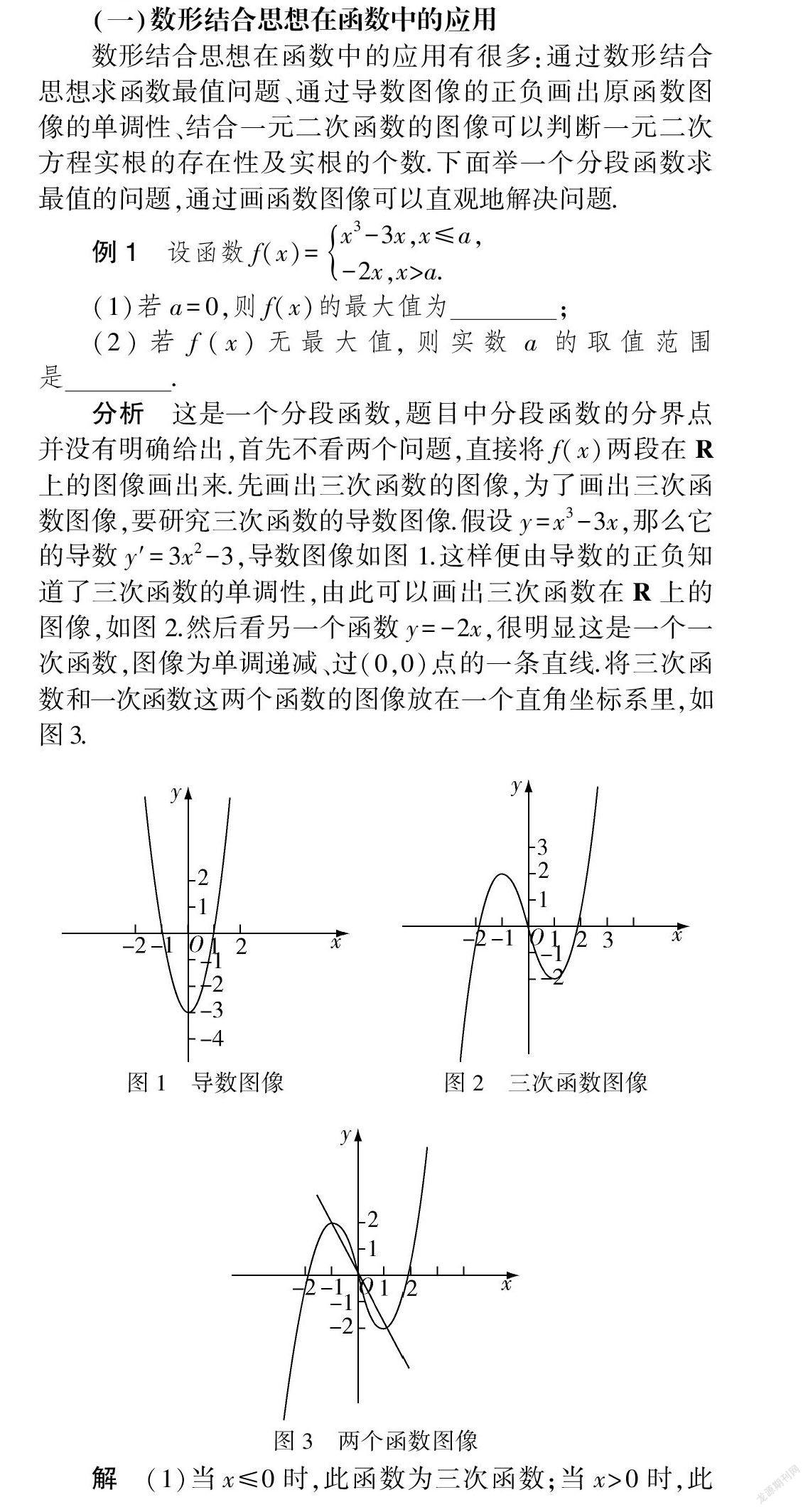
分析 這是一個分段函數，題目中分段函數的分界點并沒有明確給出，首先不看兩個問題，直接將f（x）兩段在R上的圖像畫出來.先畫出三次函數的圖像，為了畫出三次函數圖像，要研究三次函數的導數圖像.假設y=x3-3x，那么它的導數y′=3x2-3，導數圖像如圖1.這樣便由導數的正負知道了三次函數的單調性，由此可以畫出三次函數在R上的圖像，如圖2.然后看另一個函數y=-2x，很明顯這是一個一次函數，圖像為單調遞減、過（0，0）點的一條直線.將三次函數和一次函數這兩個函數的圖像放在一個直角坐標系里，如圖3.

解 （1）當x≤0時，此函數為三次函數;當x>0時，此函數為一次函數.由圖3可知，函數最大值在x=-1處取得，函數值為2.

（2）如果a<-1，結合圖3，最大值正常在一次函數上取，由于一次函數定義域是x>a，所以在一次函數上取不到最大值，滿足題意.如果a≥-1，根據圖3可知函數在x=-1時取到最大值，不符合題意. 所以實數a的取值范圍是a<-1.

（二）數形結合思想在集合中的應用

在集合的學習中，要求學生能夠理解韋恩圖所表示的集合，能夠說出集合間的基本關系.不等式的解集通常可以用數軸表示出來，將表示不等式的集合在數軸上畫出來，可以清晰地看出表示不等式的集合之間的關系.在這部分知識的學習中，需要用到數形結合思想.

例2 正確表示圖中陰影部分的是（? ）.

分析 本題要求學生用代數語言表示幾何圖形所呈現出的信息，陰影部分是在整個長方形中除去兩個橢圓，這兩個橢圓有公共部分，那么根據集合的并集和補集的定義即可求出答案.本題通過幾何與代數的結合考查了學生對集合基本運算的掌握程度.

解 用集合語言表示就是在全集U中扣除集合A和集合B的并集，即C選項的

例3 ?設集合A={x|1

分析 通過畫數軸可以直觀地看出，要使AB，那么a必須是大于2的數.然后考慮當a=2時的情況，由圖可得當a=2時，B={x|x<2}，剛好滿足AB.

解 由數軸可知，a的取值范圍是a≥2.

（三）數形結合思想在證明基本不等式時的應用

不等式是高中數學的一個重要的代數內容，基本不等式a+b2≥ab（a>0，b>0）的證明方法有很多，比如，用代數證明：

要證

ab≤a+b2，①

只要證

2ab≤a+b.②

要證②，只要證

2ab-a-b≤0.③

要證③，只要證

-a-b2≤0.④

要證④，只要證

a-b2≥0.⑤

顯然，⑤成立，當且僅當a=b時，⑤中的等號成立.以上的過程倒過來就是基本不等式的代數證明方法.

這樣的證明方法簡單易理解，但是如果和幾何圖形聯系起來證明，可以更加開闊學生的思維，發展學生直觀想象和邏輯推理的數學學科核心素養.下面是基本不等式的幾何證明方法.

如圖6，AB是半圓O的直徑，OC為半徑，F為直徑AB上的任意一點，令AF=a，BF=b，作EF⊥AB交半圓弧AB于點E，那么半圓半徑OC=a+b2.由于EF⊥AB，所以∠1+∠2=90°.由于點E為半圓弧上的點，所以AE⊥BE，即∠2+∠3=90°，所以∠1=∠3，即△AEF∽△EBF.那么有aEF=EFb，即EF=ab.

連接OE，在Rt△OEF中，斜邊OE大于直角邊EF，所以有半徑OC>EF，即a+b2>ab;當a=b時，Rt△OEF的斜邊OE等于直角邊EF，此時三角形變成一條線段，所以有OE=EF，即a+b2=ab.

于是a+b2≥ab（等號成立條件：a=b）得證.

（四）數形結合思想在立體幾何中的應用

在學習證明空間中直線與平面的位置關系、平面與平面的位置關系以及二面角的余弦值等問題時，可以根據題目情況建立一個空間直角坐標系，把所研究的立體圖形放在空間直角坐標系里，標出所需要的點的坐標，計算空間向量、方向向量等，把立體幾何問題轉化為代數的運算問題進行研究，有助于培養學生的問題解決能力.

例4 如圖7，四棱柱ABCD-A1B1C1D1的所有棱長都相等，AC∩BD=O，A1C1∩B1D1=O1，四邊形ACC1A1和四邊形BDD1B1均為矩形.

（1）求證：O1O⊥底面ABCD;

（2）若∠CBA=60°，求二面角C1-OB1-D的余弦值.

證明 （1）因為四邊形ACC1A1是矩形，所以CC1⊥AC，同理DD1⊥BD.

因為CC1∥DD1，所以CC1⊥BD，而AC∩BD=O，

因此CC1⊥底面ABCD.

由題設知O1O∥CC1，故O1O⊥底面ABCD.

解 （2）因為四棱柱ABCD-A1B1C1D1的所有棱長都相等，

所以四邊形ABCD是菱形，因此AC⊥BD.

又O1O⊥底面ABCD，從而OB，OC，OO1兩兩垂直.

如圖8，以O為坐標原點，OB，OC，OO1所在直線分別為x軸、y軸、z軸，建立空間直角坐標系O-xyz.

不妨設AB=2，因為∠CBA=60°，所以OB=3，OC=1.

于是相關各點的坐標為O（0，0，0），B1（3，0，2），C1（0，1，2）.

易知n1=（0，1，0）是平面BDD1B1的一個法向量.

設n2=（x，y，z）是平面OB1C1的法向量，則n2·OB1=0，

n2·OC1=0，即3x+2z=0，y+2z=0.

取z=-3，則x=2，y=23，所以n2=（2，23，-3）.

設二面角C1-OB1-D的大小為θ，易知θ是銳角，

于是cos θ=cos 〈n1·n2〉=n1·n2n1n2=2319=25719.

故二面角C1-OB1-D的余弦值為25719.

（五）數形結合思想在楊輝三角中的應用

楊輝是我國古代著名數學家，1261年楊輝所著的《詳解九章算法》中提出了由一組羅列的數組成的三角形，我們把它稱為楊輝三角.計數原理是高中數學重要的內容，這一章中的排列與組合和二項式定理與楊輝三角有著密不可分的聯系.

（a+b）n的二項式系數為Ckn（k=0，1，2，…，n），根據圖9可以發現，楊輝三角的第n行的第r個數可以表示為Cr-1n，第n行就是（a+b）n的展開式的二項式系數.而且二項式系數的對稱性、增減性、最大值等性質在楊輝三角的性質中都有體現.

觀察楊輝三角的規律可以發現，相鄰的兩行里除了最外邊的數，其余的數都等于它肩上的兩個數相加.也就是Crn=Cr-1n-1+Crn-1，根據組合數的性質，可以證明此式.

可見，楊輝三角的性質與二項式系數和組合數的性質有很多共同之處.這就是數學知識具有普遍聯系的體現，數形結合思想在此得到了完美的應用.在研究數學問題時，我們可以多角度出發，從不同方面研究問題.

（六）數形結合思想在方程與不等式中的應用

在初中階段，我們可以從一次函數的角度看一元一次方程、一元一次不等式.在高中階段，我們同樣可以借助二次函數來理解一元二次方程和一元二次不等式，通過函數圖像的交點情況來理解三者之間的關系.

例5 解不等式x2-12x+20<0.

分析 要想解x2-12x+20<0這個不等式，可以先觀察一元二次不等式x2-12x+20<0與二次函數y=x2-12x+20之間的關系.6431836A-566A-4583-9308-6E90413E5E21

如圖10，在平面直角坐標系中畫出y=x2-12x+20的函數圖像，函數圖像與x軸有兩個交點，這兩個交點的橫坐標就是方程x2-12x+20=0的兩個實數根，即x1=2，x2=10，所以二次函數y=x2-12x+20的圖像與x軸的兩個交點是（2，0）和（10，0）.實際上，x1=2，x2=10就是二次函數y=x2-12x+20的兩個零點.

根據函數圖像可以看出，二次函數y=x2-12x+20的零點將x軸分成三段.當210時，函數圖像在x軸上方，對應的x2-12x+20>0.

解 根據函數圖像可知，一元二次不等式x2-12x+20<0的解集是{x2

中學數學的思想方法有很多，數形結合思想是比較常見的一種思想.實際上，在中小學階段，學生就已經接觸到了這種思想.比如，在小學階段，我們解決工程中的單位“1”問題時，通常是畫一條線段，根據題意把線段分成若干份，進而更直觀地解決較難理解的代數運算問題;在初中階段，數形結合思想體現得更為直觀，比如動點問題，我們需要結合圖形中的情景進行邏輯推理與數學運算.總之，數形結合思想貫串學生數學學習的整個過程.本文簡要介紹了數形結合思想在高中數學中的應用.在高中數學的內容中，本文概述了函數、集合、基本不等式、立體幾何、楊輝三角和方程與不等式中體現出來的數形結合思想.除此之外，向量的三角形法則與平行四邊形法則用來計算向量的和與差，圓錐曲線中可以用方程的方法來描述某一點的軌跡，線性規劃通過函數圖像畫出可行域來求最值，數列的取值情況也可借助函數圖像來考慮，導數的幾何意義用切線的斜率表示，概率與統計中的幾何概型等，都體現了數形結合思想.這說明數學中的各個板塊之間的聯系需要在學習中深入研究，感悟其中蘊含的數學思想，領悟其中的解題方法.數學來源于生活，數學中解決問題可以從多個角度考慮，生活中的問題也是如此，思考問題時不能具有思維定式，要具有發散思維，要有創新意識.

【參考文獻】

[1]張連生.星推薦一本涂書（初中數學）[M].天津：天津人民出版社，2017.

[2]程曉亮，劉影.數學教學論：第2版[M].北京：北京大學出版社，2013.

[3]張茜. 高中數學中的數形結合思想研究[D].哈爾濱：哈爾濱師范大學，2019.

[4]宋佳瑋. 數形結合思想在高中數學解題中的應用探討[D].唐山：河北省唐山市第一中學高二18班， 2018.

[5]袁爽，顧洪敏，劉金英. “二次函數y=ax2的圖像”（第1課時）教學設計與點評[J].中國數學教育（初中版），2012（5）：20-24.

[6]孫義榮. 淺談數形結合思想在春季高考數學復習中的作用[J].新校園（下）， 2017（8）：59.6431836A-566A-4583-9308-6E90413E5E21