基于收益法的無形資產評估結果不確定性分析

■陳 靜 熊 袁

（1.文華學院，武漢 430074；2.武漢順海資產評估有限責任公司，武漢430060）

無形資產由于不能單獨發揮作用，且具有共益性、獨有性、累積性及復制無效等特性，使得無形資產的市場化程度較低。而隨著知識經濟的日益繁榮，越來越多的無形資產需要價值評估，在無形資產市場化程度較低的環境中，如何評估出無形資產合理的價值是比較困難和復雜的評估問題。一般的無形資產評估適宜采用收益法評估，但是收益法評估出來的結果會受收集的數據是否全面、收入預測的可實現性、評估人員選取的參數是否合理等因素的影響，導致評估結果具有較強的不確定性。如何對評估結果進行再分析，獲得一個更合理的評估值是本案例深入討論的問題。

一、理論陳述

（一）敏感性分析

敏感性分析多用于項目的可行性研究和項目評估，是分析項目投資、成交價、成本、產量以及工期等主要變量發生變化時，導致項目經濟效益的主要指標發生變動一種分析方法，一般的分析指標包括：項目內部收益率、凈現值、投資回收期等。通過敏感性分析，要在諸多的不確定因素中，找出對經濟效益指標反應敏感的因素，并確定其影響程度，計算出這些因素在一定范圍內變化時，有關效益指標變動的數量，從而建立主要變量因素與經濟效益指標之間的對應定量關系。敏感度分析一般使用的是單因素敏感性分析，在其他變量不變的前提下，選擇某一項變量作為不確定因素，對所選定的需要進行分析的不確定性因素，按照一定的變化幅度，如±5%，±10%等，改變其數值，然后計算出這種變化對經濟評價指標的影響數值，并將其與該指標的原始值相比較，從而得出該指標的變化率，可用公式表示：

依次計算出每一個變量引起的經濟評價指標的變動率，把所有的變動率進行對比，對引起經濟評價指標變動率大的因素即為最敏感因素。

（二）期望值理論

期望值理論是美國耶魯大學教授、心理學家弗羅姆（V.Vroom）首先提出的。弗羅姆的基本觀點是人之所以能夠積極地從事某項工作，是因為這項工作或組織目標會幫助他們達成自己的目標，滿足自己某方面的需要。運用在數學上，期望值也稱數學期望，指一個人對某目標能夠實現的概率估計，即：一個人對目標估計可以實現,這時概率為最大（P=1）；反之,估計完全不可能實現，這時概率為最小（p=0）。而大部分期望是隨機事件的各種變量與相應概率的加權平均值。不確定因素可能發生的變化值為隨機變量，其出現的可能性大小為隨機變量的概率。一系列隨機變量所發生的概率排序成為概率分析，一個事件發生的全部概率分布的總和為1，期望值就代表了不確定因素在實際中最可能出現的數值。

隨機變量可分為離散型隨機變量和連續性隨機變量。離散型隨機變量是指事件發生的可能性變化為有限次數，并且每次發生的概率值為確定的隨機變量。其期望值計算公式為：

式中：E（x）——期望值

Xi——隨機變量值

i——隨機變量的序數，等于1，2，3，…，n

P——隨機變量發生的概率

連續型隨機變量是指事件發生的可能變化在有限的區間內可以無限次數且其概率的總和為1 的隨機變量。其期望值計算公式為：

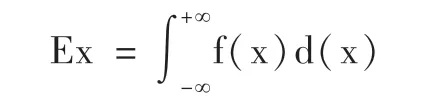
式中：f（x）——隨機變量的變化函數

得出評估結果后，將引用上述兩點理論，做敏感性分析及期望值的測算，結合評估實務操作，最終得出區間性評估結果及相關可實現概率。

二、應用示例

（一）案例基本情況

A 公司擬與B 公司共同投資組建C 公司，公司注冊資本200 萬元，為專業制作某電子運輸設備（系列產品）。根據出資協議，A 公司以技術出資；B公司以貨幣資金出資。B 公司要求引入評估公司對該項出資技術進行價值評估，要求評估報告在明確具體評估值后，給出區間評估的結果及實現概率。

本次評估對象和范圍為一項專有技術，且該專有技術為擬組建公司的唯一核心生產技術。根據評估人員收集的可行性研究報告表明，該擬組建公司與擬定評估基準日已具備生產能力，未來五年的收入預測分別為1 000 萬元、1 200 萬元、1 500 萬元、1 800 萬元及2 000 萬元。經評估人員收集相關市場材料及與投資人的溝通訪談，了解到該專有技術已經在原工廠實施運作，根據原公司已有客戶及擬組建公司的生產規模，認定預測收入能夠實現。折現率16%，技術使用提成率2.17%，所得稅稅率25%。

計算該專有技術的評估值，計算過程略，具體見表2-1。

表2-1 采用專利提成率法計算表 （單位：萬元）

因此，該專有技術評估值=14.03+14.51+15.64+1 6.18+15.50=75.86（萬元）

（二）對評估過程的分析

該項資產評估主要使用的收益法，影響評估結果的參數主要有預期收益、折現率以及獲益年限三項指標。

首先，由于無形資產不能單獨獲利，必須與其他資產共同發揮作用，即需要從使用無形資產獲得的權益中分離出無形資產獲取的預期收益，以上案例使用了提成率法，即用“收入預測×提成率”，這里的收入預測需要評估人員通過技術、市場、資產結構等方面去分析判斷得出的，受到評估人員的經驗和收集的數據有限的影響，結果具有一定的主觀性和不確定性。同時，提成率一般會參考國內外的統計數據，一般的數據均為一個區間值，如上例中電力行業的無形資產提成率為0.99%-2.97%（見表2-2），在具體計算時，取值2.17。這個取值也是評估人員根據自己的經驗進行判斷后選擇的數值，同樣具有不確定性。

表2-2 各行業無形資產銷售收入提成率

其次，無形資產收益折現率的估計，需要對無形資產轉化形成的產品和服務的市場風險、技術風險、經營風險、財務風險等特有風險的判斷及量化，具有較強的不確定性。

第三，無形資產收益年限也需要進行判斷估計。

綜上，由于無形資產獨有性及市場化程度低，這些參數的估計大都沒有源于有效市場的參考信息。因此，在評定估算中有較多和較大的不確定性，對評估結果的合理性判斷帶來了困難。而從本案例來說，無形資產的收益年限只計算5年，應該是充分考慮的無形資產的先進性以及合同約定的限制，因此不考慮其影響力。故本案例選取的不確定性因素為收入預測、提成率以及折現率三項。

（三）對評估結果的不確定性分析

1、敏感性分析

收入預測、提成率以及折現率三個可變因素在初始值的基礎上按±10%的變化幅度變動，計算相對應的評估結果的變化情況，得出結果如表2-3所示。

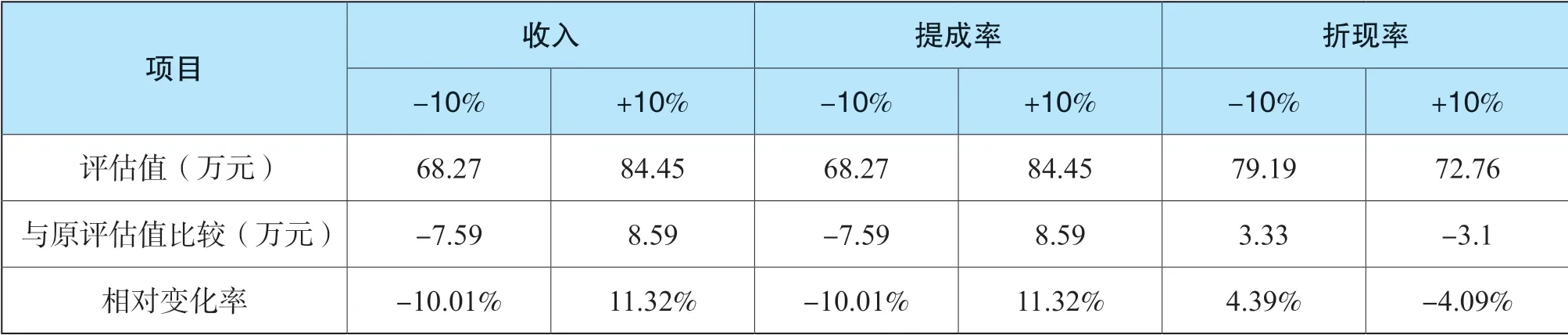
表2-3 敏感度分析表

由表2-3 可以看出，在各個變量因素變化率相同的情況下，收入和提成率的變動情況是一致的，每變動±1%，評估結果變動幅度為-1% ～1.13%，而折現率每變動±1 %，評估結果變動幅度為-0.41%～0.44%。

綜上分析，收入與提成率相對來說對評估結果敏感度較高，該評估值受收入及提成率因數影響較大。比較收入和提成率發生變化的可能性，一般情況下，未來收益的預測發生變化的概率較大，很多因素是不可控的；而提成率受當事人雙方的談判技巧影響，會有一定的變動區間，但是變化是可控的。因此，評估結果的使用者在參考評估結果時，應重點關注收入情況，一旦影響環境發生較大的變化時，需要對評估結果進行相應的變動。同時在后期風險預防中應關注收入的實現等相關問題并設計相關保證收入實現的風險防范措施。

2、期望值分析

期望值分析依舊可以選擇以上三個不確定因素來分析。設定不確定因素變化情況及發生概率，各事項發生概率及評估值，加權評估值計算見表2-4。

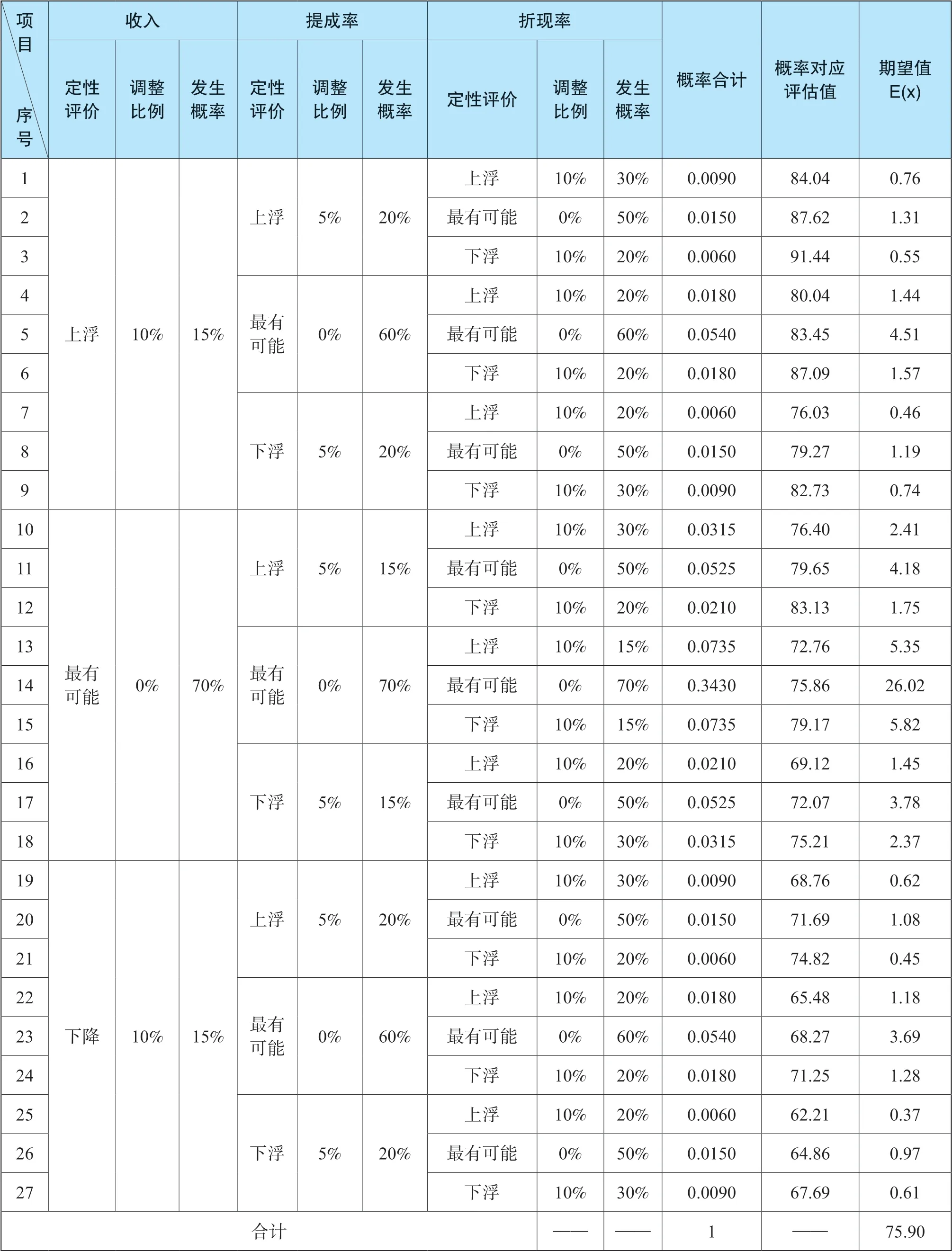
表2-4 期望值計算一覽表

標準方差的求取過程

=5.02（萬元）

在進行概率分析中，一般可根據期望值與標準方差確定其有效益水平及獲得這一水平的可能性：

E（x）±σ 的可能性為68.27%；

E（x）±2σ 的可能性為95.49%；

E（x）±3σ 的可能性為99.73%。

故，該項目評估的區間值及區間概率為：

70.87 萬元～80.92 萬元的可能性為68.27%；

65.85 萬元～85.94 萬元的可能性為95.49%；

60.83 萬元～90.96 萬元的可能性為99.73%。

變異系數U 為：

5.02÷75.90=0.0661

以上計算結果表明，評估值75.86 萬元的實現在可能性為68.27%區間范圍內，對于非技術投資方，建議將技術出資額控制在70.87 萬元以下，具有較高的可實行性。

三、結論

本文通過對無形資產常用的基本方法——收益法的相關基本參數取值全過程進行追溯和分析，發現未來的收入預測、無形資產提成率以及折現率三項因素的取值由于受到收集的數據全面與否、評估人員的經驗等因素所限，會影響無形資產最終評估值。

再通過敏感性分析得出收入預測對評估結果的影響最大，而通過期望值分析得出70.87 萬元為更合理的評估結果。在評估實務中，如果評估人員在報告中給出評估結論的同時，對評估結果進行敏感性分析和期望值分析，最終得出區間評估結果，有利于報告使用人更為理性的使用評估結果。同時，根據這一方法，評估人員也能夠通過可實現程度的概率評價，分析出更合理的評估結果。

本文提出對無形資產評估結果“再評估”的概念，對獲取無形資產合理的評估結果提供了一種技術解決思路，該技術思路中評估結果敏感性分析、期望值分析等技術要點也可以推廣用于評估計算中當評估參數不確定因素較多或較大的情形，如用收益評估其他資產及市場法、成本法的評估應用中。