巧用分數單位,讓深度學習真正發生
邵申華











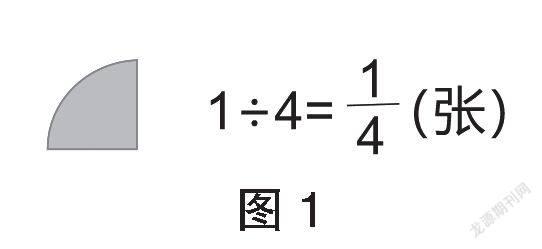




摘 要:深度學習,是一種深層次的學習模式,進行深度學習,不僅能讓學生真正參與學習,還能讓學生在深度學習的過程中體驗成功,獲得發展,提升自身的數學核心素養[1]。基于此,筆者以“分數與除法的關系”一課的教學為例,探討引領學生開展深度學習的過程,讓學生真正參與學習研究,完善學生對分數的認知,進而提高學生的學科素養。
關鍵詞:深度學習;分數單位;真分數;假分數
小學高年級的學生在口算練習中,遇到類似1÷2、2÷3、5÷4這樣的題,往往喜歡用小數來表示兩個數相除的結果,哪怕像2÷3計算結果除不盡,學生也喜歡用保留兩位小數的近似數。像5÷4這個算式,學生最容易接受的就是用小數來表示結果,如果用分數來表示,是一個假分數。在小學階段,學生對“分數是一個數”的意識還不夠強。分數對于學生來說并不陌生,學生從蘇教版教材三年級上冊就開始認識分數了,但到了五年級下冊才真正系統地學習分數。學生在相當長的一段時間內,更愿意把分數看作一種除法的運算,而忽視了分數是一個數的性質,并且在這個過程中,大多數學生對真分數有非常深刻的記憶,認為分子比分母小的數才是分數,對分數的意義出現片面性的理解。如何改變這一現狀?筆者以“分數與除法的關系”這一課為例,突破傳統的思維模式,充分利用分數單位的作用,體現分數單位的價值,讓學生更好地理解分數,使學生真正進入深度學習。
一、深度參與,初步感知分數與除法的關系
在五年級下冊第四單元《分數的意義和性質》的第一節課中,“分數單位”是這樣定義的:把單位“1”平均分成若干份,表示其中一份的數,叫作分數單位。但是,通過這個定義,學生們很難真正感受到分數單位存在的必要性,也不能真正理解分數單位的價值。在“分數與除法的關系”一課的
【教學過程】
師:將一張圓片平均分給4個同學,每人分得幾張?能列出算式嗎?
生:1÷4=0.25(張)
師:除了0.25,還有不同的表示方法嗎,誰來說說自己的想法?
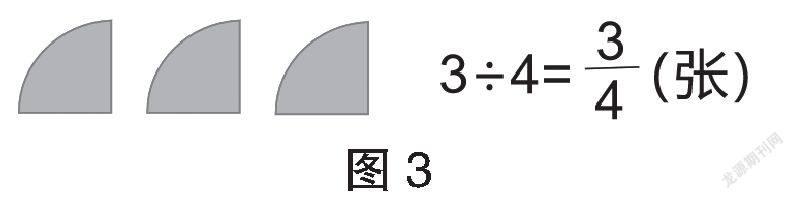
生:把一張圓片平均分成4份,其中1份是,每個人分得張。
二、深度體驗,體會分數與除法的關系
深度學習的核心是教師通過對問題情境與任務的細致設計,激發學生的認知沖突,并組織他們進行深入的探究學習。為此,筆者延續以上情境,既然一張圓片可以平均分,那么把幾張圓片平均分給4個學生呢?學生在情境的引導下,會舉出很多的例子。筆者有目的地將學生分成兩組:一組學生的信封里有3張圓片,學生需要研究如何把3張圓片平均分給4個同學;另一組學生的信封里有5張圓片,學生需要研究如何把5張圓片平均分給4個同學。面對3張圓片,學生會受到一定的思維沖擊,產生一定的認知沖突,他們一開始覺得不能分,再經過思考,一般會出現以下兩種情況。
【教學過程】
師:同學們,既然一張圓片可以平均分給4個同學,那么你們還能把幾張圓片平均分給4個同學呢?怎么列式?(學生舉例)
師:這個算式的結果是多少呢?下面大家2人一組,通過分圓片繼續研究。(研究算式3÷4)
師:給你3張圓片,請你介紹一下你是怎么分的?
(1)一張一張分
師:剛才他們是一張一張分的,還可以怎么分?
(2)三張一起分
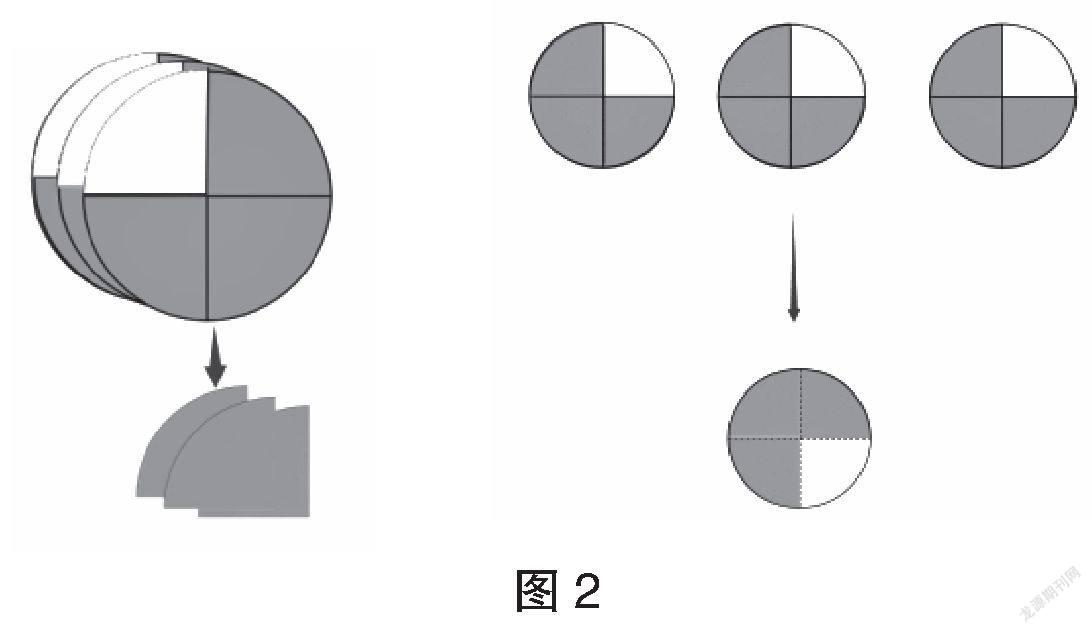
生:我把3張圓片疊在一起分,平均分成4份。每人分得其中的一份。
師:為了看得更清楚,請你用剪刀把三張圓片平均分成4份。
學生剪開圓片,將圓片平均分成4份。
師:你能拿出其中的一份嗎?
師:這一份是幾張?
師:這兩種分法有什么不同?
生:分法不同,一種是一張一張分,一種是三張一起分。
師:以上兩種情況分別可以把什么看作單位“1”?
生:第一種是把1個圓看作單位“1”,第二種把3個圓看作單位“1”。
師:它們有什么相同呢?
三、深度探究,自然感受假分數的產生
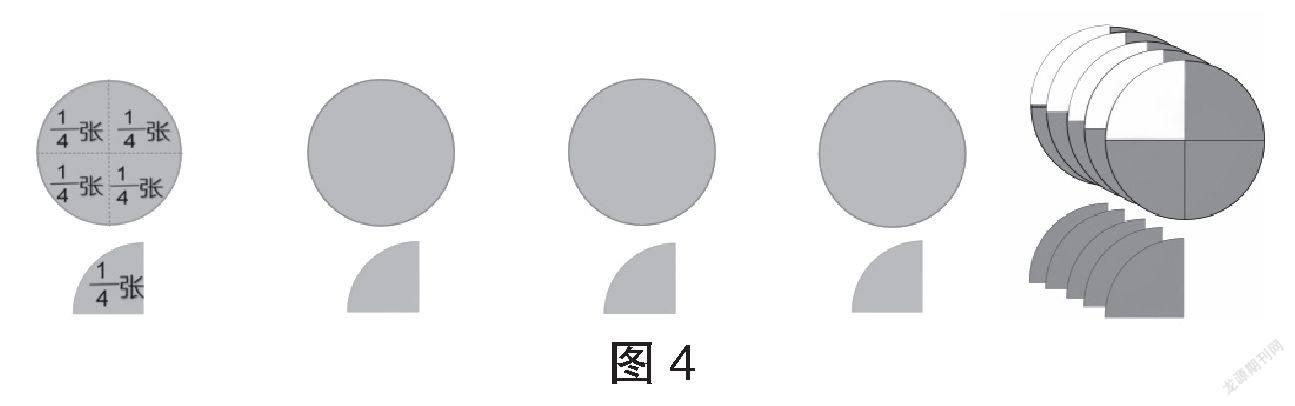
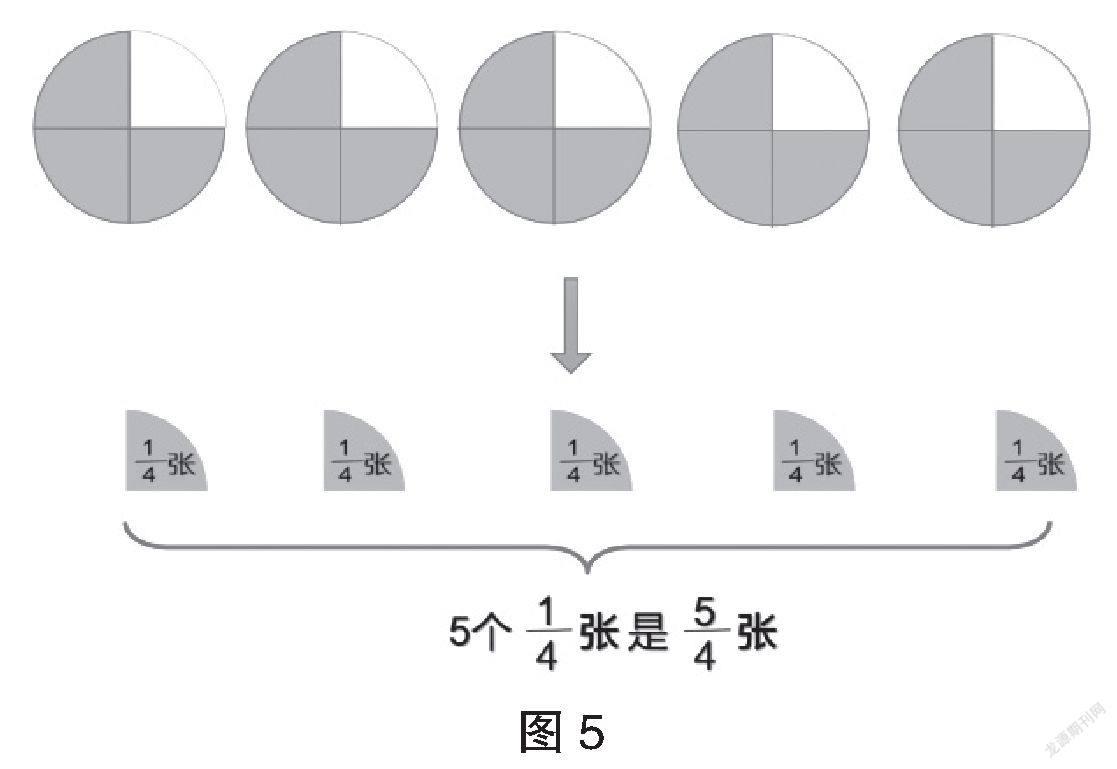
分數是由分數單位的累積而來,分數單位的累積是“N進制計數法”。當分數單位的累積超過1時,就自然而然地產生了假分數。在一組學生研究3張圓片平均分給4個同學的同時,另外一組學生把5張圓片平均分給4個同學。相比3張圓片平均分給4個同學,5張圓片的分法更加豐富。
【教學過程】
師:有研究算式5÷4的嗎?說說你是怎么分的?
四、深度運用,豐富學生對分數的認識
5除以4產生了假分數,在學生的認知里第一次出現了分子比分母大的分數,有的學生可能一時還不能完全接受。筆者再次和學生總結回顧,通過結合圖形,建立模型,讓學生想象分數單位的累積,知道任意兩個自然數相除的商都可以用分數來表示,可以是分子比分母小,也可以是分子比分母大,這樣就可以擴大分數的概念,并為研究分數和除法之間的關系提供了更多豐富的資料。
【教學過程】
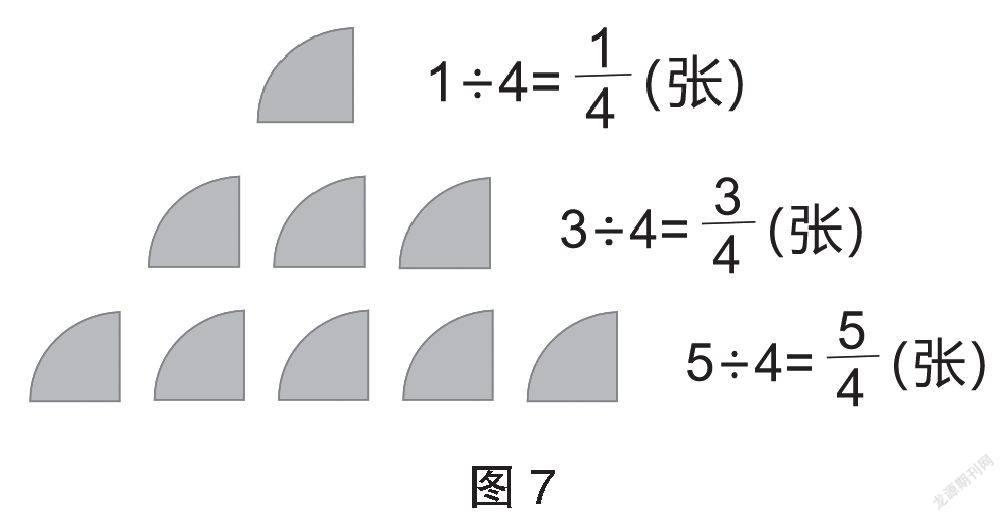
師:請你推想一下,7÷4=?9÷4=?
師:同學們,觀察這些除法算式,它們的商都可以用分數來表示。分數與除法之間有什么關系呢?
生:被除數相當于分數的分子,除數相當于分數的分母。
師:被除數÷除數的商是不是也可以寫成分數的形式呢?
生:可以。
生:b不能是0。
師:看來,兩個數相除的商,可以用分數表示。這就是分數和除法的關系。像這樣的例子,你還能繼續列舉嗎?
在深度學習中,遷移與應用是一種重要的學習方法。通過分數單位的累積,學生不用動手操作分一分,就能將方法遷移并運用到更多的除法算式中,從而直接口算出類似7÷4、9÷4這樣的算式的結果,這得益于教師在前面教學過程中的兩次舉例:第一次是讓學生根據1張圓片可以平均分給4個學生,舉例還能把幾張圓片平均分給4個學生,本例旨在探討兩個數相除的商是否能用分數表示,從而為抽象的分數與除法之間的關系提供具體資料,讓學生更容易理解;第二次舉例,學生在分數單位的累積的過程中,不僅掌握了真分數,還理解了假分數,填補了學生對于分數認知的空白。正如張奠宙教授所說:“由份數定義到商定義,是數系的擴充,這是一次跨越、一次升華,每個學生都必須面對。”[3]教師通過這一階段的教學,讓學生從運算的角度理解分數的必要性,并將除法運算和分數的數學知識聯系起來。
深度學習是由點到線再到面的綜合學習,在這節課中,筆者以分數單位的累積為基礎,幫助學生厘清分數和除法的關系。分數單位累積的過程中,筆者突破了單個知識點教學的局限,將教材中相關聯的知識進行了整合,由真分數自然而然地過渡到假分數,糾正了學生對“分子比分母小”的片面認識,使學生對分數有了更全面、更深入的理解,讓學生對分數的認識從“份數定義”向“商定義”轉變。在學生自主建構分數與除法的關系的過程中,自然而然地打通了學生學習與發展的內部轉換過程,推動了學生的知識探索,培養了學生的高階思維,提高了學生的學科素養,使深度學習真正在課堂發生。
[參考文獻]
馬云鵬.深度學習:走向核心素養(學科教學指南·小學數學)[M].北京:教育科學出版社,2019.
吳建芳.分數單位有什么價值:《分數與除法的關系》與《真分數和假分數》課時整合教學實踐[J].名師在線,2018(23):65-66.
張奠宙.話說分數(上)[J].小學教學(數學版),2007(6):46-47.

