融合多角度信息和圖卷積網絡的社交網絡節點分類模型

劉 超，梁安婷，劉小洋，黃賢英

(重慶理工大學 計算機科學與工程學院， 重慶 400054)

0 引言

當前各種在線交流分享平臺發展迅猛，產生大量社交網絡數據。這些數據蘊含著個體信息、個體活動及個體間的交互信息，能體現用戶的屬性與偏好，展示用戶之間的關系等。如何挖掘社交網絡數據中的信息，利用其價值一直備受研究者們關注。節點分類是將代表實體的節點進行類別劃分，是社交網絡的研究熱點之一，有著重要的實際應用價值，例如在交流分享平臺中(微博、抖音等)，對用戶進行精確分類，有助于后續為用戶推薦共同點更多的好友及可能感興趣的事件，增強用戶的使用體驗；在電商平臺中(淘寶、京東等)，精確分類買家有助于商家的把控和售賣，提高交易成功的概率。然而如何從節點自身屬性和網絡結構中提取更多的信息，有效融合這些信息，實現社交網絡節點分類任務依然是個有待研究的問題。

同質性(homophily)和共引規律(co-citation regularity)是社會科學中的2種重要性質，源于人與人之間的交流來往。社交網絡是人際網絡的延伸，已有研究[1-3]證明社交網絡同樣具備上述性質。研究者已經利用這2種性質對社交網絡問題進行了一些探索，如Getoor[4]對網絡數據的近似推理算法進行了比較，在社交網絡中，同質性是應用到鏈接分類的鏈接模式之一，并且鏈接到相同文檔的文檔很可能具有相同標簽；Bhagat等[5]在處理帶權邊的多重圖的標記問題時，分別利用同質性和共引規律提出了兩類算法，兩類算法在博客的標簽分配上分別取得了較好的效果。這些研究表明，在社交網絡的研究中，利用同質性和共引規律能提升解決相關問題的性能，遺憾的是，研究尚未應用到社交網絡節點分類，同時，在2種性質和節點自身信息及網絡拓撲結構的融合問題上，沒有相關文獻進行探討。為了利用2種性質更好地挖掘并融合網絡拓撲和節點自身屬性，在圖卷積網絡(graph convolutional network,GCN)的基礎上進行改進，提出能融合更多信息的模型，提高節點分類效果。基于同質性和共引規律，提取出同質型節點和共引型節點兩類節點。通過相似度度量算法，計算被分類節點與其他所有節點特征向量的相似度，找到相似度最高的前k1個節點作為該節點的同質型節點；計算被分類節點與其他所有節點的鄰接向量的相似度，找到相似度最高的前k2個節點作為該節點的共引型節點。對被分類節點與對應的同質型節點進行鏈接，構成同質矩陣空間，同理，對被分類節點與對應共引型節點進行鏈接，構成共引矩陣空間。分別在2種矩陣空間進行卷積，提取相應的節點信息，對被分類節點進行信息補充，提高分類精確度。

在Wang等[6]的研究基礎上，利用上述兩類節點，挖掘更全面的信息并進行融合，提出融合多角度信息和圖卷積網絡的社交網絡節點分類模型(a social network node classification model based on multi-angle information fusion and graph convolutional network,MAIF-GCN)。主要貢獻如下：

1) 提取蘊含著節點同質信息和共引信息的兩類關系型節點。①同質型節點：和被分類節點有著相似屬性(特征向量相似度高)的節點；②共引型節點：和被分類節點鏈接著更多相同節點(鄰接向量相似度高)的節點。提取兩類關系節點的信息，即挖掘被分類節點的隱藏信息，后續實驗證明，提出的兩類關系節點能對被分類的社交網絡節點信息進行更好地補充，對社交網絡節點分類有益。

2) 提出一種新的融合多角度信息和圖卷積網絡的節點分類模型MAIF-GCN。從鄰接鄰居、同質最近鄰和共引最近鄰多個角度挖掘被分類節點的相關信息，通過平均嵌入相加、注意力機制進行信息融合，實驗證明，該模型在傳統社交網絡數據集上取得很好的分類效果。

1 相關工作

Kipf等[7]和Defferrard等[8]提出的GCN能有效捕捉節點的相關信息，在節點分類問題上表現出很好的分類效果，是處理節點分類問題的常用方法。如Derr等[9]利用平衡理論來正確地匯總和傳播經過簽名的GCN模型各層的信息，使分類問題泛化至社交媒體中的簽名網絡(或既有正面鏈接又有負面鏈接的圖表)；Hu等[10]為了增加接收域，提出了一種新的深度層次圖卷積網絡(hierarchical graph convolutional networks,H-GCN)用于半監督節點分類；Lin等[11]提出了基于圖卷積網絡的結構融合，從多視圖數據的多圖結構中挖掘出更完整的分布結構，以半監督的方式提高引文網絡節點分類性能。

GCN的巨大成功部分歸功于它提供了一種基于拓撲結構和節點特征的融合策略來學習節點嵌入，然而，最近的一些研究揭示了GCN在融合節點特征和拓撲結構方面的某些弱點。例如，Li等[12]的研究表明，GCN實際上對節點特征進行了拉普拉斯平滑，使嵌入到整個網絡中的節點逐漸收斂；Hoang等[13]和Wu等[14]證明了特征信息在網絡拓撲結構上傳播時，拓撲結構對節點特征起到低通濾波的作用；Wang等[6]通過實驗證明，GCN對網絡拓撲結構和節點特征的融合能力與最佳甚至令人滿意的距離相去甚遠。

無法充分融合節點自身屬性和網絡拓撲結構來提取相關信息，可能會嚴重影響GCN在分類任務中的性能，為解決此問題，不少研究者在GCN的基礎上進行改進：Velikovi等[15]提出了圖注意網絡(graph attention network,GATs) ，他們為一個鄰域中的不同節點指定不同的權值，以此調整從鄰居節點接收的信息量，提高分類精確度；Abu-El-Haija等[16]提出了一個利用鄰接矩陣的多次冪的圖卷積層，通過堆疊高階卷積層獲取更多信息，達到提高分類精度的效果；Wu等[17]提出了一個名為DEMO-Net(degree-specific graph neural networks)的通用圖神經網絡模型，該模型根據節點的度值將特征聚合表達為一個多任務學習問題。這些改進方法都在一定程度上提高了節點分類的精度，在處理節點分類問題上起著不可忽視的作用，可見，更好地融合網絡拓撲結構和節點信息，更多地提取相關信息，是提高節點分類效果的先決條件，是解決節點分類問題的重要目標。

Bhagat等[18]在發表的社交網絡節點分類研究綜述中，提到社交網絡存在的2個重要特性：一為同質性，即個體之間的聯系與那些在本質上相似的個體相關；二為共引規律，即相似的人傾向于提及或聯系相同的事物。然而，對這2個重要特性的研究尚未應用到社交網絡節點分類領域。Wang等[6]就GCNs能否在信息豐富的復雜圖中最優地整合節點特征和拓撲結構進行研究，針對GCNs融合節點特征和拓撲結構的能力不夠理想的缺陷，提出了一種用于半監督分類的自適應多通道圖卷積網絡(adaptive multi-channel graph convolutional networks,AM-GCN)。其核心思想是同時從節點特征、拓撲結構及其組合中提取特定的和共同的嵌入，并利用注意機制學習自適應嵌入的重要性權重。在進行節點特征和拓撲結構信息融合的過程中，AM-GCN無意識地使用了同質性，受其使用方法的啟發，本文中從理論上證明為何該構建方法能夠對分類點信息進行補充，并進一步添加共引規律，構建能提取更多信息、融合信息更完整的分類模型。

2 提出的MAIF-GCN模型

2.1 問題描述

為研究社交網絡節點分類問題，在給定圖數據G= (A,X)的條件下，盡可能精確地將圖中的n個節點分為C類中的某一類，使用的符號定義即變量描述如表1所示。

表1 符號定義

為解決上述問題，提出了融合多角度信息和圖卷積網絡的節點分類MAIF-GCN模型，模型概覽如圖1所示。

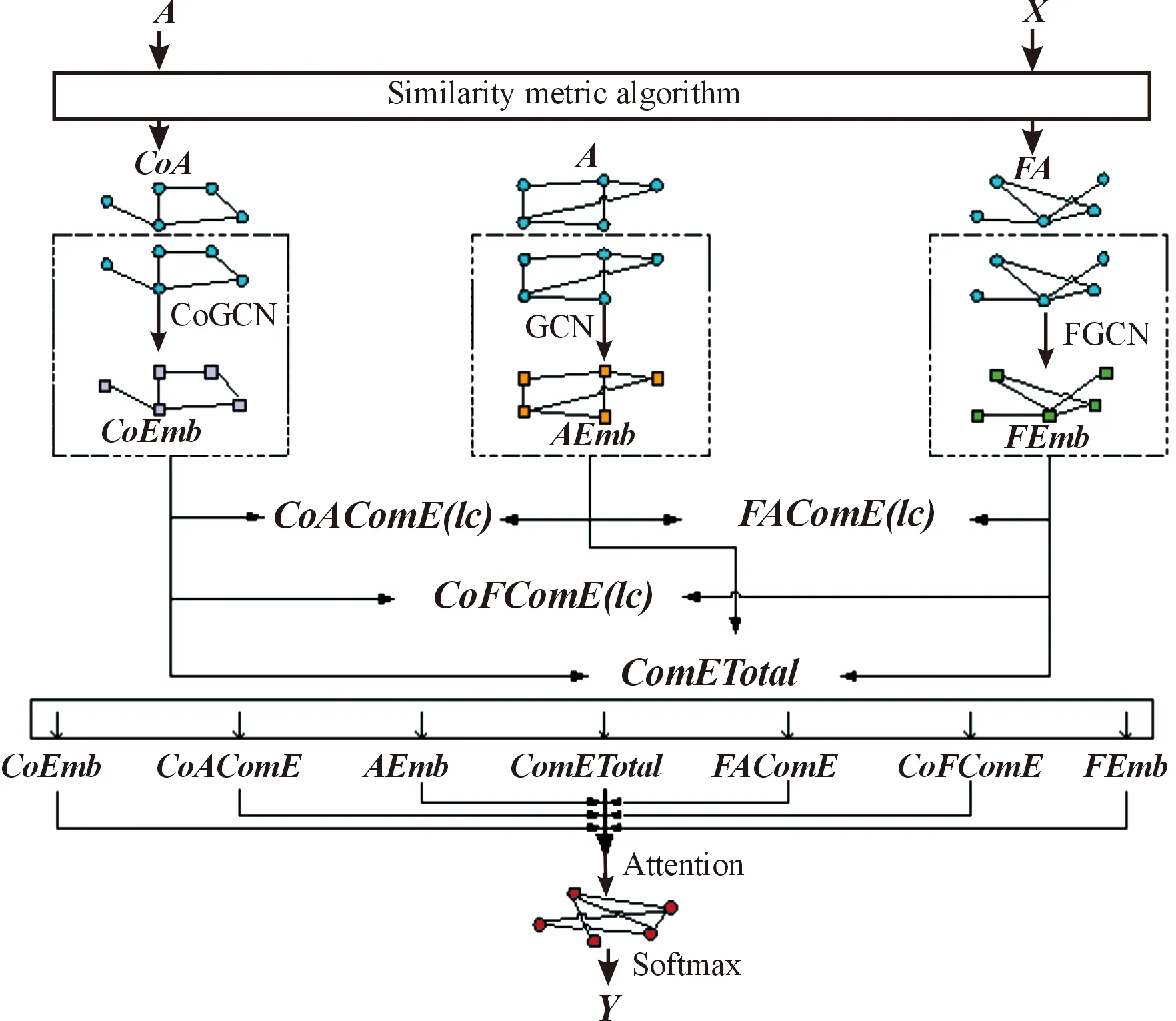
圖1 融合多角度信息和圖卷積網絡的社交網絡節點分類模型(MAIF-GCN)

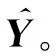
2.2 構造2個矩陣空間

為了提高社交網絡節點分類精度，基于社會科學中確定的2個可以應用于在線社交網絡的重要現象——同質性和共引規律，提出兩類能為分類節點提供有用信息的相關節點——同質型節點和共引型節點。為挖掘兩類節點信息，構造相應的關系矩陣空間，在構建好的關系矩陣空間中進行卷積操作，就能融合相應關系的節點信息。

X是特征向量矩陣，該矩陣每一行代表著一個節點的特征，將一行向量同其他所有行向量進行相似度的計算，便能求得這些其他節點同這個節點在特征即性質上的相似程度。通過對特征向量矩陣的每一行和其他行進行相似度的計算，得出和每個節點性質最相似的k1個節點。將“性質相似”這種聯系作為邊，相似度最高的k1個節點將產生鏈接，由此得出每個節點的同質向量FAi∈R1×n，將所有節點的同質向量拼接起來，得到同質矩陣空間FA∈Rn×n。

A是鄰接矩陣，該矩陣每一行代表著一個節點同其他節點的聯系，存在聯系則為1，否則為0。將一行向量同其他所有行的向量進行相似度的計算，便能求得其他所有節點同該節點偏好或傾向最相近的k2個節點。將“偏好或傾向相近”這種聯系作為邊，傾向相近度最高的幾個節點將產生鏈接，否則不鏈接，由此得出每個節點的共引向量CoAi∈R1×n，將所有節點的共引向量拼接起來，得到共引矩陣空間CoA∈Rn×n。

經過上述理論鋪墊發現，2種矩陣空間都是由求解向量間相似度獲取的。常見的相似度的計算有歐幾里得度量、皮爾遜相關系數、余弦相似度等。通過對比計算，幾種相似度度量算法對最近鄰的計算結果幾乎一致，此種算法的選擇不影響最終分類結果。本文中最終使用余弦相似度進行相似度的度量：

(1)

2.3 提出的融合多角度信息和圖卷積網絡的社交網絡節點分類模型MAIF-GCN

2.3.1獲取空間嵌入

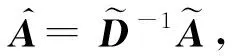
在共引矩陣空間進行圖卷積，提取并融合共引型節點的節點信息，得到共引矩陣空間卷積后的嵌入ZCo(CoEmb)， 其中，Wco是在共引矩陣空間進行學習的權重矩陣：

(2)

在鄰接矩陣空間進行圖卷積，提取并融合鄰居節點的節點信息，得到鄰接矩陣空間卷積后的嵌入ZA(AEmb)，其中，WA是在鄰接矩陣空間進行學習的權重矩陣：

(3)

在同質矩陣空間進行圖卷積，提取并融合同質型節點的節點信息，得到同質矩陣空間卷積后的嵌入ZF(FEmb)，其中，WF是在同質矩陣空間進行學習的權重矩陣：

(4)

2.3.2融合空間嵌入

不同社交網絡中，三類節點向被分類節點提供的信息的重要程度不同，有時可能只有單一類型的節點提供對分類有幫助的信息，但有時需要2種或3種關系節點共同提供信息。

鄰接矩陣空間、同質矩陣空間和共引矩陣空間3種單空間都經過了相同的預處理，因此在3種單空間進行卷積后的嵌入輸出格式一致，即矩陣大小一致，可以直接進行加減。 將單空間嵌入通過相加平均進行組合，節點會融合不同空間卷積后的信息，得到聯合嵌入。

將單空間嵌入、兩兩單空間聯合嵌入和3個單空間聯合嵌入共同放進注意力機制進行融合，得到最終嵌入，同時獲得各種嵌入的重要性。由上述獲取聯合空間嵌入的操作易知，單空間嵌入與聯合空間嵌入輸出格式一致。將所有嵌入在第二維上進行拼接，得到每個節點在不同角度上的多維表示。本文的注意力機制使用兩層全連接進行學習，再通過softmax函數，從每個節點在不同角度上的多維表示，學習到分類該節點時在每個角度，即每種嵌入上所占的比重。

1) 組合單空間嵌入(eg：共引與鄰接單空間嵌入組合ZCoA(CoAComE)，3個單空間嵌入組合ZTotal(ComETotal))：

(5)

(6)

2) 融合空間嵌入：

(αCo,αA,αF,αCoA,αFA,αCoF,αTotal)=

att(ZCo,ZA,ZF,ZCoA,ZFA,ZCoF,ZTotal)

(7)

將3種單空間嵌入和聯合嵌入共同放進注意力機制，通過注意力機制得到每個節點對應各種嵌入的重要性，使用該表示重要性的向量將各種嵌入融合起來，得到終極嵌入Z(Emb)：

Z=αCo·ZCo+αA·ZA+αF·ZF+

αCoA·ZCoA+αFA·ZFA+αCoF·ZCoF+

αTotal·ZTotal

(8)

2.3.3半監督多標簽分類

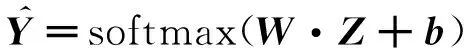
(9)

2.3.4約束和目標函數

1) 一致性約束

考慮到雖然提取信息的角度不同，但最終信息給予的對象是同一節點，因此，這些不同的信息會有些許相似或存在某種聯系。通過將不同關系矩陣空間中提取到的信息進行相互約束，使得挖掘到的信息更有利于分類。這種相互約束，就是提取出的信息的一致性約束。

各嵌入在正則化后乘以自身的轉置轉化為對稱矩陣，用對稱矩陣的最小二乘進行一致性約束。鄰接矩陣嵌入ZA正則化后表示為ZAnor，同理，同質矩陣嵌入、共引矩陣嵌入正則化后的表示為ZFnor、ZConor。正則化后的不同空間嵌入乘以自身的轉置轉化為對稱矩陣，分別得對稱陣如下：

(10)

以鄰接矩陣和同質矩陣為例，用最小二乘得此2種空間嵌入的一致性約束LCoA如下：

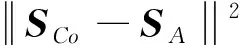
(11)

同理可得鄰矩和共引矩陣嵌入的一致性約束LFA，同質矩陣和共引矩陣嵌入的一致性約束LCoF。不同網絡對于矩陣空間的相似性要求不同，通過對一致性約束進行加權相加，得到總的一致性約束：

(12)

式中：α、β為超參數，不同網絡通過調節α、β來調整各空間嵌入的一致性約束。

2) 目標函數

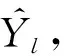
(13)

3) 綜合目標函數

結合一致性約束和目標函數，得到模型的綜合目標函數L：

L=Lt+θ·LCom

(14)

式中：θ為超參數，不同網絡的數據集在經此模型訓練時，通過調節此超參數對一致性約束的權重進行調整。

算法1模型算法流程。

輸入：社交網絡圖數據G=(A,X)，L個帶標簽的樣本節點；

1) 通過式(1)得到FA和CoA；

repeat：

3) 通過式(2)—(4)分別計算得到單空間嵌入ZCo、ZA和ZF，通過式(5)與式(6)獲取組合空間嵌入ZCoA、ZFA、ZCoF與ZTotal；

4) 使用式(7)獲得不同嵌入的比重(αCo,αA,αF,αCoA,αFA,αCoF,αTotal)，式(8)加權融合，得到最終嵌入Z；

6) 通過式(10)—(12)計算一致性約束LCom，式(13)進行交叉熵損失求和，得到Lt；

7) 使用式(14)得到綜合目標函數L；

8) 梯度下降法更新模型參數；

until 滿足訓練停止條件

3 實驗與結果分析

3.1 實驗設置

3.1.1數據描述

使用2個傳統社交網絡數據集BlogCatalog[19]和Flickr[19](數據集信息見表2)，以分類準確率(accuracy)與F1-measure作為度量指標，測試本文提出的MAIF-GCN模型。在BlogCatalog和Flickr數據集上，將本文模型與傳統的社交網絡節點分類算法及一些先進的GCNs變體模型進行對比，并結合試驗結果對模型進行分析。

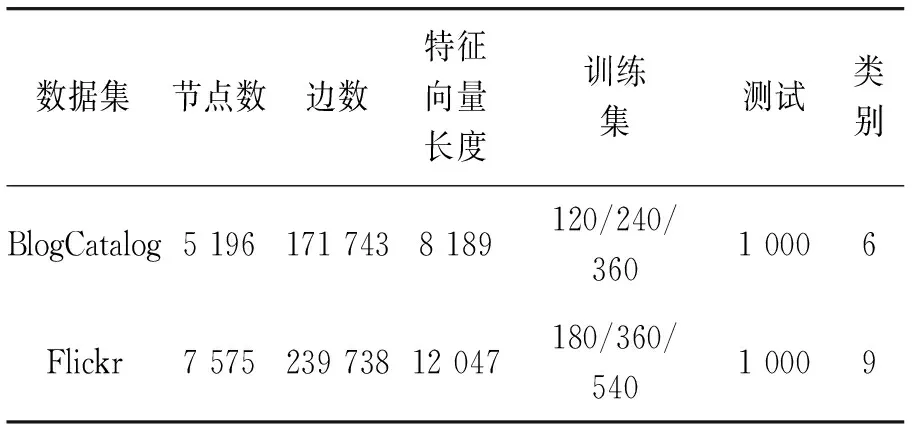
表2 用于模型測試的數據集信息

1) BlogCatalog數據集：一個社會關系網絡。節點屬性由用戶配置文件的關鍵字構造，圖是由博主和他(她)的社會關系(比如好友)組成，標簽代表作者提供的主題類別，所有節點劃分為6類。

2) Flickr數據集：Flickr是用戶分享圖片和視頻的社交網絡。節點表示Flickr中的用戶，圖是用戶之間的好友關系，標簽用于標識用戶的興趣小組，所有節點劃分為9類。

3.1.2對比實驗

將MAIF-GCN模型與6種先進且效果良好的圖神經模型進行對比，對比模型詳情如下：

1) GCN[7]：一種半監督圖卷積網絡模型，它通過聚合鄰居的信息來學習節點表示。

2) Chebyshev[8]：一種基于切比雪夫濾波器的GCN方法。

3) GAT[15]：一種利用注意機制聚集節點特征的圖神經網絡模型。

4) DEMO-Net[17]：一種用于節點分類的度數特定圖神經網絡。

5) MixHop[16]：一種基于GCN的方法，在一個圖卷積層中混合高階鄰居的特征表示。

6) AM-GCN[6]：一種用于半監督分類的自適應多通道圖卷積網絡。

3.1.3參數設置

如表2數據集所示，訓練集有3種標簽率(如BlogCatalog數據集存在120、240、360個標簽節點)，2個數據集都選擇1 000個節點作為測試集。所有對比模型都在他們相應論文建議的參數基礎上進行調優，以求更高的精度。除本文模型外，模型AM-GCN的分類結果都優于其他模型，為了方便對比，本文模型與AM-CGN模型共有的參數，取值與該模型一致，在3個不同的矩陣空間進行兩層圖卷積，2個數據集的隱藏層nhid1都是512，輸出層nhid2都是128；120個標簽節點的BlogCatalog數據集使用0.000 2的學習率進行Adam優化，180個標簽節點的Flickr數據集使用0.000 3，除此之外，2個數據集的其他訓練集都用0.000 5作為優化函數的學習率。一致性約束系數θ和所取同質型節點的個數k1及共引型節點的個數k2值將在后文進行討論，根據分析結果取值，最終設置BlogCatalog數據集的一致性約束系數θ為1，k1取值為5，k2取值為6；Flickr數據集的一致性約束系數θ為0.1，k1取值為6，k2取值為3。

3.2 實驗結果與分析

3.2.1實驗結果

社交網絡節點分類對比實驗結果見表3。由實驗結果可以得出，MAIF-GCN的準確率(Accuracy)與F1-measure在2個數據集上都優于所有對比模型。事實上，除卻本文中提出的MAIF-GCN，AM-GCN的準確率和F1-measure都是最高的， 已被提出者證明其信息融合能力的優越，而MAIF-GCN在此模型分類結果的基礎上，將BlogCatalog數據集的分類精確度和F1-measure指標提高3%及以上，將Flickr數據集的分類精確度提高3%及以上、F1-measure指標提高2%及以上，充分說明本文模型在引入社會科學中的2種性質后，具有更進一步的信息挖掘與融合能力，證明了提出的兩類型節點在解決社交網絡節點分類時具有積極作用。

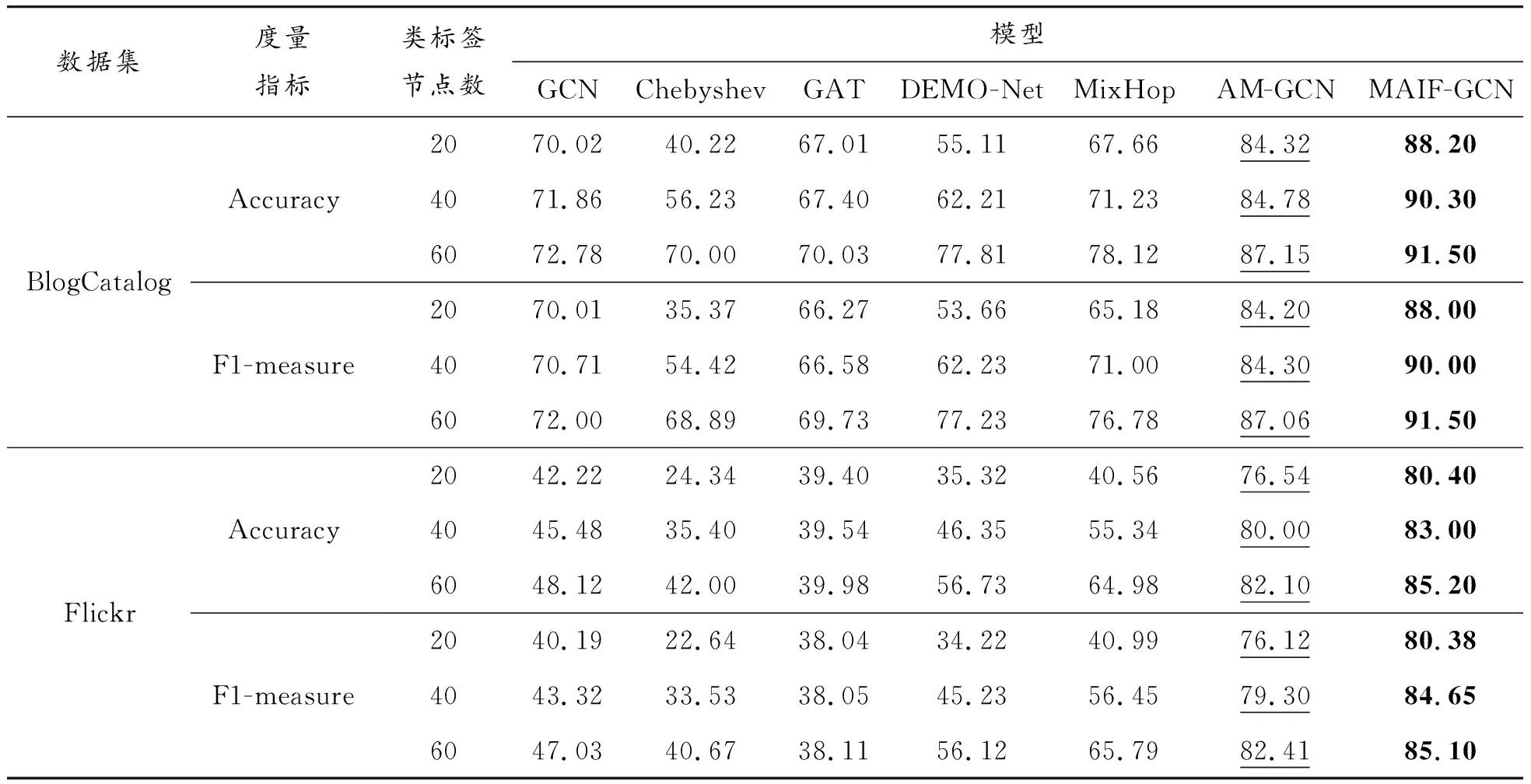
表3 社交網絡節點分類實驗結果

3.2.2嵌入分布分析

可視化各種嵌入方式的占比，直觀表示不同嵌入方式在分類時的占比情況，觀測提取的兩類型節點在社交網絡節點分類中的作用。單空間嵌入、兩兩單空間聯合嵌入和3個單空間聯合嵌入共同放進注意力機制進行融合，在得到最終嵌入的同時，獲得各種嵌入的重要性。下載訓練過程中各嵌入的注意力值，使用箱須圖進行繪制，得到嵌入分布分析如圖2所示。

Blogcatalog數據集上各嵌入方式(箱須圖橫軸從左往右)占比均值分別為：0.013，0.434，0.149，0.045，0.265，0.029，0.065；Flickr數據集上分別為：0.010，0.822，0.017，0.026，0.094，0.011，0.020。

從圖2和嵌入占比均值可以直觀地看到每種嵌入的分布情況，并且總結出以下結論：① 同質矩陣單空間嵌入在2種數據集中都占比最高，遠超傳統鄰矩，充分說明在社交網絡節點分類中，同質型節點對分類節點的正向作用；② 同質和共引矩陣空間的融合嵌入在2種數據集的嵌入中都占比次高，且在2個數據集的嵌入中，共引矩陣單空間嵌入都比鄰接矩陣單空間嵌入要高，這兩點證實了共引型節點同樣對被分類節點的精確分類有益；③ 單空間嵌入占比較大，但融合嵌入的比例同樣不可忽視，因此，在社交網絡節點分類時，要挖掘融合多方面的信息，才能對節點進行精確分類。

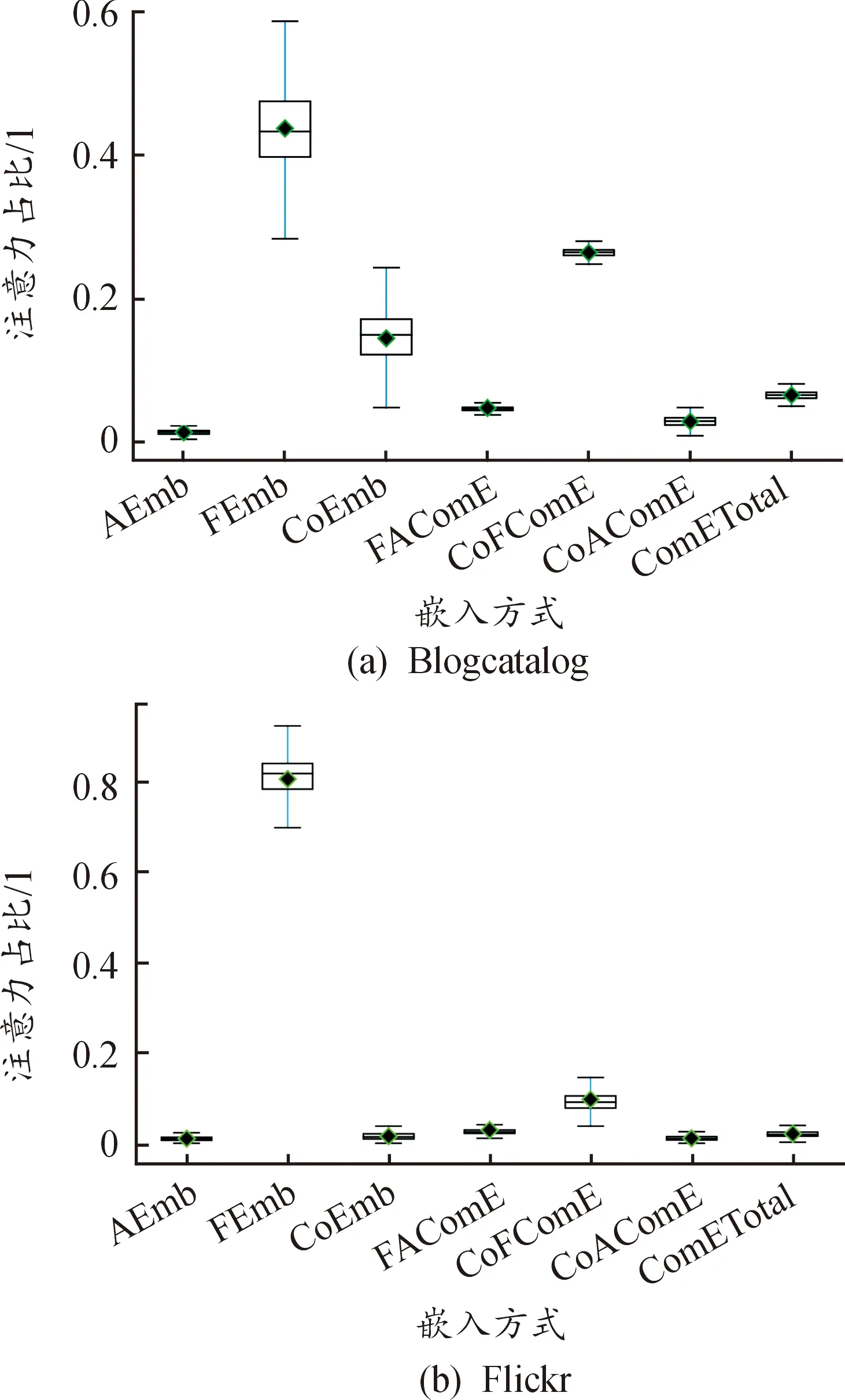
圖2 嵌入分布分析

3.2.3參數分析

本文模型的超參數有k1、k2、θ、α、β。參數k1和k2是獲取的：“近鄰”個數，這里的“近鄰”并非直觀意義上的位置相近，而是同質或共引意義相近。基于六度空間理論，k1、k2取值范圍以數字6為中心，分別測試兩類型的“近鄰”個數從2～9對分類產生的影響。圖3展示了k1取值(2～9)對節點分類精度的影響，圖4展示了k2取值(2～9)對節點分類精度的影響。

圖3 參數k1分析

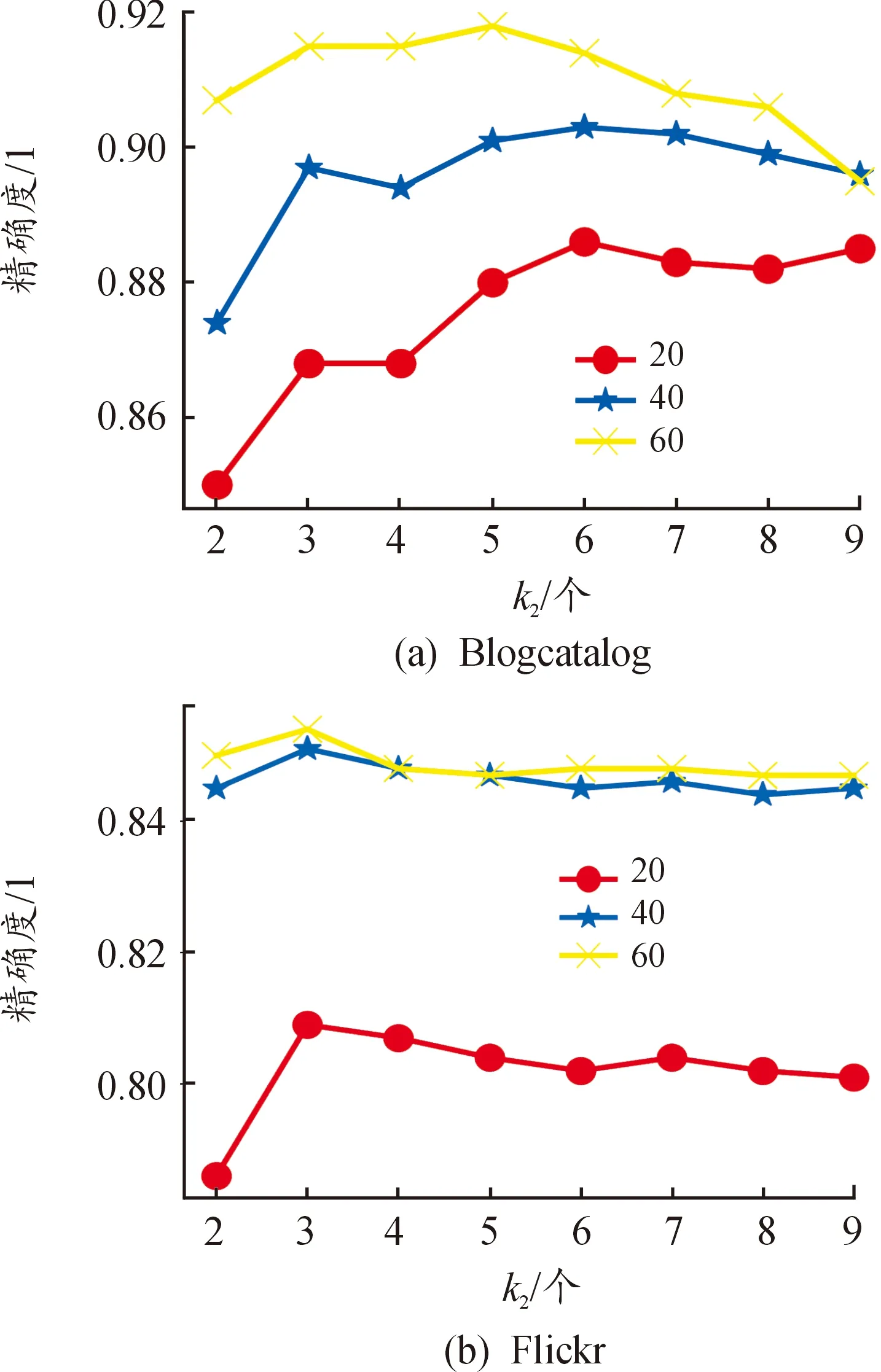
圖4 參數k2分析

參數θ是損失函數中共同一致性約束的系數，調整θ即改變一致性約束對節點分類影響的力度，圖5展示了θ取值(0.000 1～10 000)對節點分類精度的影響。

α、β是共同一致性約束中，2種單獨一致性約束的系數，調節α、β值，就能調整3種單獨一致性約束在共同一致性約束中的占比。3種約束的占比情況由α、β共同決定，2個參數的實驗數據單獨進行可視化不夠直觀，將每組α、β的實驗數據同時繪制，以便分析出更合理的超參數配比。圖6、圖7分別展示了α、β取值(0.000 1～10 000)對Blogcatalog、Flickr數據集節點分類精度的影響。

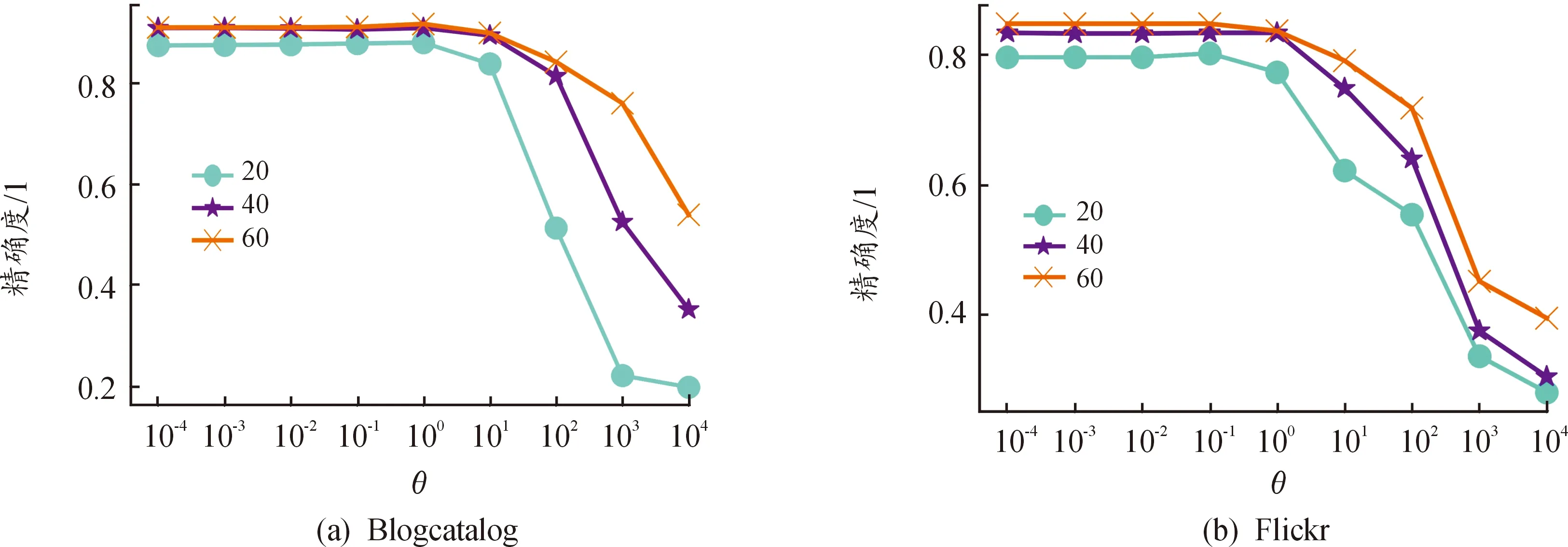
圖5 參數θ分析

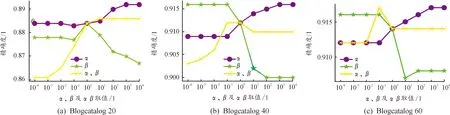
圖6 參數α、β分析(Blogcatalog)

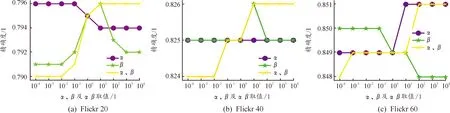
圖7 參數α、β分析(Flickr)

同質最“近鄰”參數k1的分析見圖3，BlogCatalog隨著k1值的增加，分類精確度先增加再減少，類標簽數為20、40、60的數據集分別在k1取5、8、4處獲得最優。這可能是因為BlogCatalog隨著圖變得更密集，特征平滑，而且更大的k1可能引入更多的噪聲連邊。而Flickr的精確度在中間存在小波峰，隨著k1值的增加，精確度先增大后減小再趨于平緩，它可能同樣受特征平滑和噪聲的影響，類標簽數為20、40、60的Flickr數據集都在k1取6或9處獲得最優。

共引最“近鄰”參數k2的分析見圖4。圖4中，BlogCatalog在類標簽數為20時，精確度隨k2的增加先增大后減小再趨于平緩，k2在6或9處取得最優；當標記數據增多，隨著k2值的增加，BlogCatalog的分類精確度先增加再減少，與k1情況相似，可能因BlogCatalog變得密集，特征平滑，或引入更多的噪聲連邊，類標簽數為40和60的BlogCatalog數據集分別在k2取6和5處獲得最優效果。Flickr的精確度波動小，同樣是隨著k2值的增加，精確度先增大后減小，原因與BlogCatalog數據集一致，類標簽數為20、40、60的Flickr數據集，都在k2取3時獲得最佳效果。

共同一致性約束θ的分析見圖5，2個數據集的精確度，都隨著一致性約束系數θ的增加，先非常緩慢的上升，而后，BlogCatalog數據集以1為拐點，Flickr數據集以0.1為拐點，精確度隨著θ值的增加下降。兩數據集分別在θ取1和0.1左右獲得最優效果。現象表明，2個數據集都不期望從3個空間中提取出太相似的信息。

一致性約束系數α、β分析見圖6、圖7。如圖6(a)所示，圓形標記實線是超參數α的消融實驗結果，此時β恒為1(第3種單獨約束系數一直為1)，反映α對應的單獨約束的占比對分類結果的影響；星形標記線是超參數β的消融實驗結果，此時α恒為1，反映β對應的單獨約束的占比對分類結果的影響；X形標記線是超參數α、β同時進行消融實驗的結果，此時第3種單獨約束仍為1，α、β取值的一致變化將改變第3種單獨約束的占比，反映了第3種單獨約束的占比對分類結果的影響，α、β取值越大，第3種約束占比越小。將每個數據集的3種單獨約束對分類結果的影響可視化到同一張圖上，觀測分析超參數α、β的配比。

圖6中，所有子圖中的圓形標記線大體呈上升趨勢，α取值大，分類效果較好；子圖(a)中除波峰，星形標記線大體呈下降趨勢，β取值較小，分類效果好；子圖(c)中除波峰，星形標記線大體呈上升趨勢，說明第3種約束占比小，α、β取值大于等于1(第3種單獨約束系數一直為1)。子圖(a)中，在類標簽數為20的Blogcatalog數據集中，圓形標記實線大體呈上升趨勢，在1 000處達到峰值，星形標記線在1處取得最大值，X形標記線在10處取得最大值，再往后對精確度沒有影響，說明α對應約束占比最大，第3種約束占比最小，β值對應約束較為折中取得最佳效果，但因X形標記線后面趨于平緩，α取值不適宜過大。綜上，α值取100左右，β值取10左右時，模型效果較好；在類標簽數為40和60的Blogcatalog數據集中，圓形標記實線呈上升趨勢，在1 000處達到峰值，星形標記線和X形標記線都在0.1處取得最大值，β對應約束應比另外兩約束小，α值取10左右，β值取0.1左右時，模型效果較好。

圖7中，3個子圖的圓形標記實線和星形標記線走向幾乎相反，說明在Flickr數據集上，類標簽個數對一致性約束占比有影響，需要逐個分析。圖7(a)中，圓形標記實線在0.1處取得最大值，星形標記線和X形標記線都在10處取得最大值，α值對應一致性約束占比小，β值對應一致性約束占比大，第3種約束占比小。綜上，在類標簽數為20的Flickr數據集上，α值取1,獲得的模型效果較好，β值取10左右模型效果較好。圖7(b)中，圓形標記實線不隨值的變化改變走向，星形標記線和X形標記線都在10處取得最大值，β值對應一致性約束占比大，第3種約束占比小，α值對應一致性約束的占比比β大，比第3種約束小，α值取5左右，β值取10左右獲取的模型效果較好。圖7(c)中，圓形標記實線在10處達到最大值，且取值再往上精確度不變，星形標記線在0.1處取得最大值，X形標記線在100處取得最大值，第3種約束占比最小。綜上，α值對應約束占比大，β值對應約束占比小，但比第3種約束占比大，α值取5左右，β值取10左右獲取的模型效果較好。

對不同數據集，給出的α、β近似值的模型的分類結果比取距離該近似值較遠的值高0.2%～0.8%，且分類精確度對α、β的取值不敏感，一定范圍(20左右)內變化非常小，可忽略不計。

3.2.4剝離實驗分析

為了進一步評估本文模型各模塊的有效性，進行剝離實驗，將MAIF-GCN及其4種變體在所有數據集上的分類結果進行比較。對比分類實驗結果見表4。

1) GCN：沒有同質矩陣空間和共引矩陣空間的MAIF-GCN模型。不存在同質矩陣空間和共引矩陣空間的嵌入，節點只在鄰接矩陣空間進行卷積操作，進而分類，模型退化為傳統的GCN模型。

2) MAIF-GCN-F：沒有同質矩陣空間的MAIF-GCN模型(只有鄰接矩陣嵌入、共引矩陣嵌入及兩者的組合嵌入)。

3) MAIF-GCN-Co：沒有共引矩陣空間的MAIF-GCN模型(只有鄰接矩陣嵌入、同質矩陣嵌入及兩者的組合嵌入)。

4) MAIF-GCN-cst：去掉一致性約束的MAIF-GCN模型。不對各單空間嵌入進行一致性約束，只通過模型訓練，將各種嵌入進行組合和融合，進而進行分類的MAIF-GCN模型。

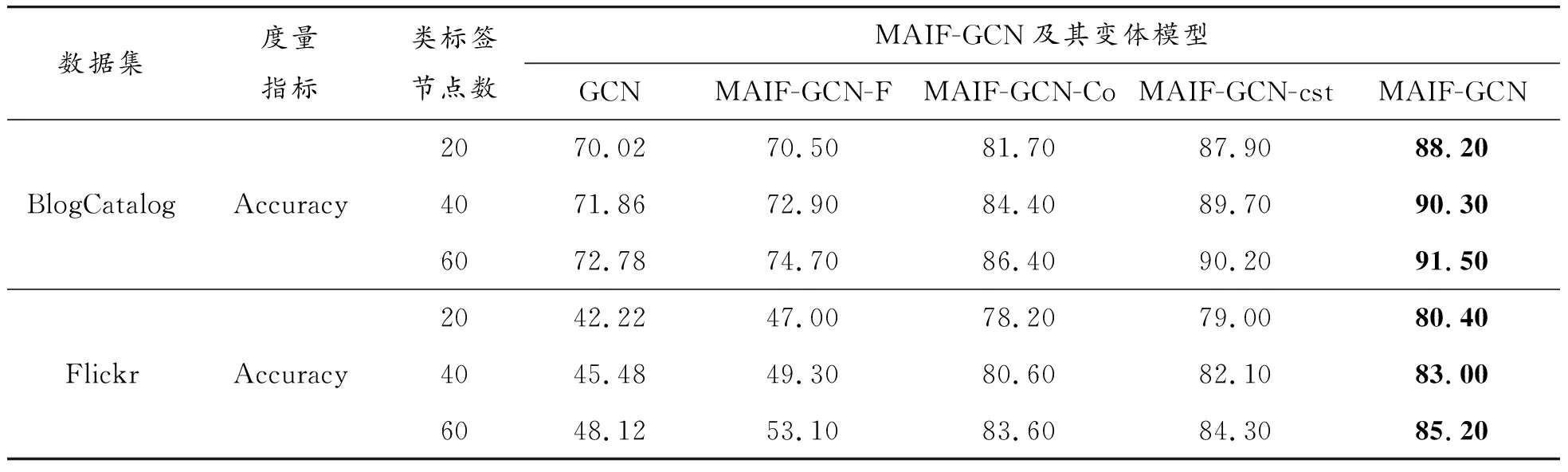
表4 MAIF-GCN及其變體模型節點分類實驗結果

分析表4，可以得出以下結論：① MAIF-GCN的結果始終優于其他4種變體，表明引入并結合利用同質矩陣和共引矩陣空間，進行3種單空間嵌入的一致性約束是有效的。② MAIF-GCN-F和MAIF-GCN-Co的分類精確度都比GCN的高，分別表明了共引矩陣空間和同質矩陣空間的有效性。③ MAIF-GCN-Co的結果比MAIF-GCN-F好，意味著同質性在本模型中起著更重要的作用。④ 對比MAIF-GCN-cst和表3中的其他實驗結果可以發現，MAIF-GCN-cst雖然沒進行約束，但仍取得了對抗baseline的非常有競爭力的表現。

3.2.5不同類型數據集驗證實驗

為了進一步驗證所提出模型的效性，驗證利用2種性質在解決社交網絡節點分類問題時真實有效，使用不同類型的數據集進行對比實驗分析。

將社交網絡數據集ego-Facebook[20]中的2個網絡進行處理，用于節點分類對比實驗。該數據集因收集的節點特征不同分為10個小網絡，取其中缺失標簽較少、節點個數較多，且類別較多的網絡0(后稱FaceNet_0)和網絡1912(后稱FaceNet_1912)進行實驗，清洗掉網絡中缺失特征或標簽的節點，進行數據規整化后進行分類，驗證模型在分類類別較多時的性能。同時，使用另一社區檢測數據集UAI2010和其他2個不同類型的數據集進行對比實驗分析，對比本文模型在不同類型數據集上的分類效果。驗證實驗數據集信息見表5。

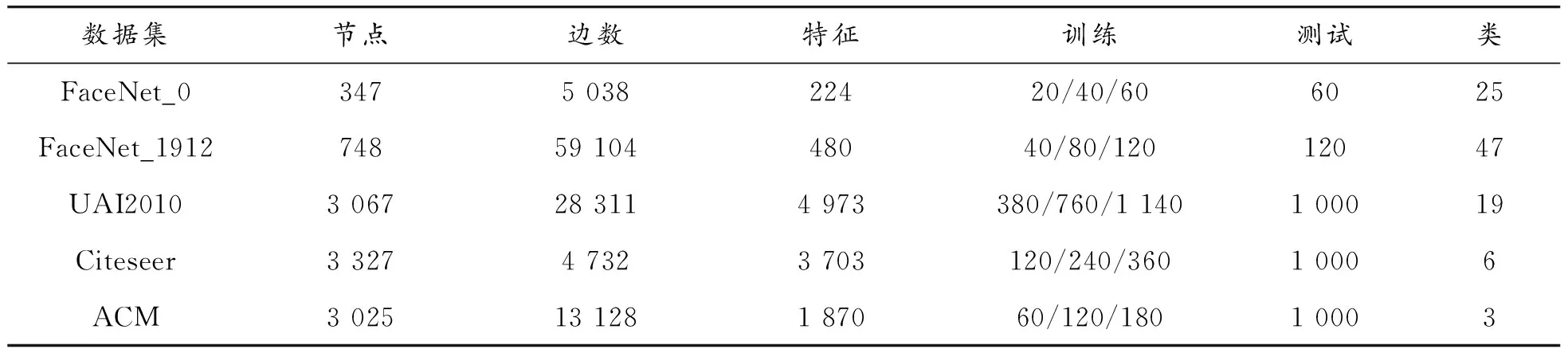
表5 用于模型驗證的數據集信息

1) FaceNet_0[20]：Facebook社交網絡小子集，節點特征為Facebook用戶的性別、生日等屬性信息，圖由用戶間的朋友關系組成，將用戶所屬的圈子作為類別，所有節點劃分為25類。

2) FaceNet_1912[20]：Facebook社交網絡小子集，節點特征為Facebook用戶的性別、生日等屬性信息(與Facebook_0不完全相同)，圖由用戶間的朋友關系組成，將用戶所屬的圈子作為類別，所有節點劃分為47類。

3) Citeseer[7]：引文網絡。節點代表文章，圖表示文章之間的引用關系，標簽用于識別文章所屬的類別，所有節點劃分為6類。

4) UAI2010[21]：一個已經在圖卷積網絡中進行了社區檢測測試的數據集，所有節點劃分為19類。

5) ACM[22]：從ACM數據集中提取，節點代表文章，特征是文章關鍵詞的詞袋表示，圖的連邊代表兩篇論文出自同一作者，所有節點劃分為3類。

不同類型的數據集進行節點分類的實驗結果見表6。本小節所有對比模型都在相應論文建議的參數基礎上進行調優，以求更高的精度。

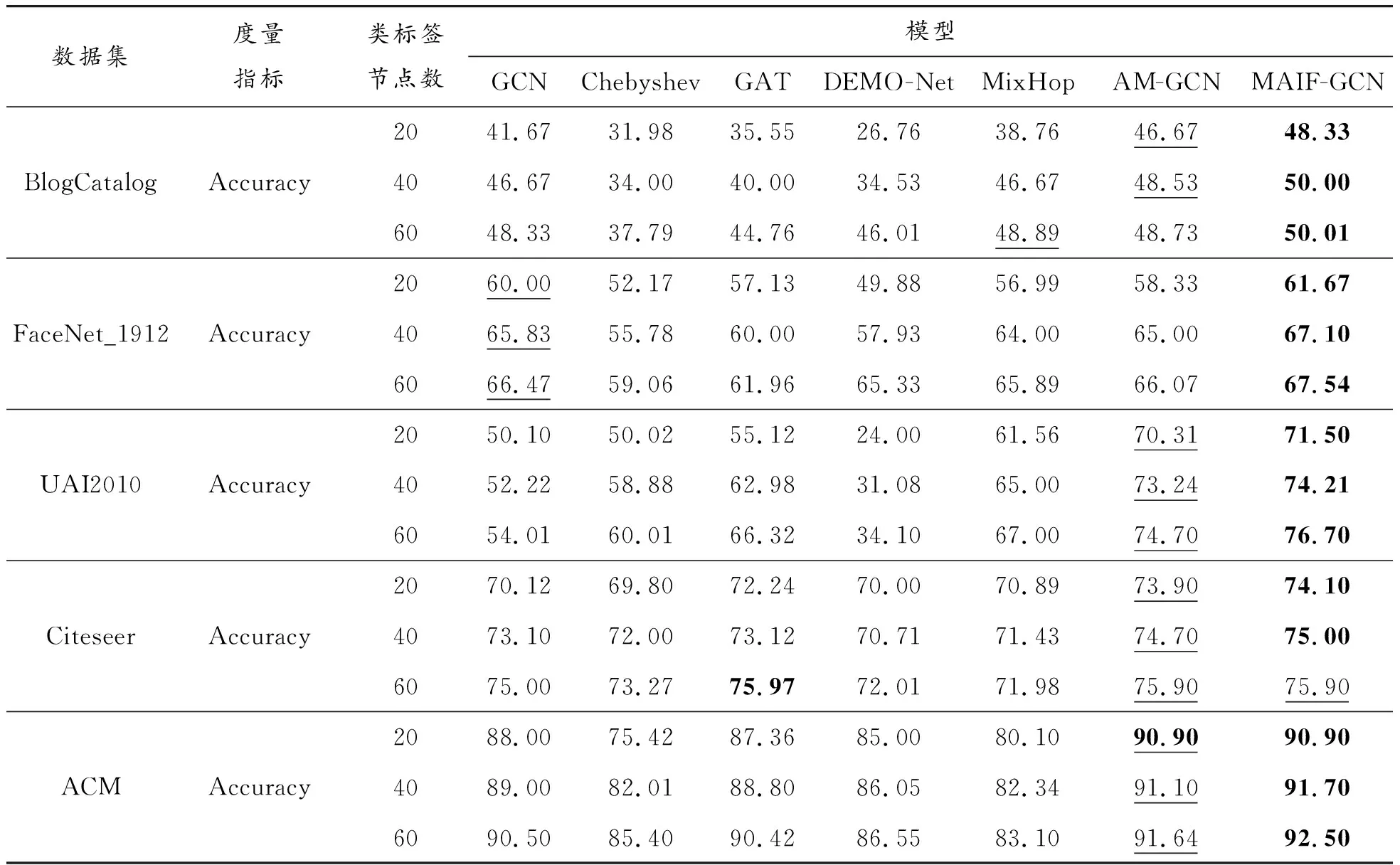
表6 不同類型數據集實驗結果

通過實驗結果可以看到：MAIF-GCN在前3個數據集上的分類結果明顯優于其他模型，提高1%及以上；MAIF-GCN作用于后2個數據集上時，鮮少有分類精度不變或降低的情況，有的數據集存在較小提升。前3個數據集是社交網絡數據集(UAI2010是用于社區探測的數據集，能夠歸為社交網絡一列)，網絡存在本文模型引入的2種性質，因此本文模型能夠產生效用，從對比實驗結果看也的確如此。后2個數據集不屬于社交網絡范疇，模型引入的2種性質不一定存在于后2種網絡，從結果也可以看出，后2個數據集分類精度雖提升卻有限，且存在不提升或略有降低的情況，但不提升和降低的情況極少，多數精度仍是提升的。由實驗結果分析得出：

1) MAIF-GCN在處理社交網絡節點分類的問題上具有積極作用；在不同的社交網絡數據集上總能取得較好的效果體現了MAIF-GCN的泛化能力。

2) 其他類型數據集上的分類精度不提升或降低的情況極少，展現了MAIF-GCN的優越性。

4 結論

根據社交網絡中存在的同質性和共引規律這2種性質，提取出兩類對社交網絡中被分類節點產生正向影響的節點：①和被分類節點有著相似屬性(相似特征向量)的同質型節點；②和被分類節點鏈接著較多相同節點(相似領域節點)的共引型節點。分別計算特征向量和鄰接矩陣中鏈接向量的相似程度，選取同質性相似度最高的前k1個節點和共引性相似度最高的前k2個節點，構建兩類型節點相應的同質矩陣空間和共引矩陣空間。在構建的2個矩陣空間進行卷積，融合相應類型的節點信息。為了更好地融合各角度提取到的信息，除了單獨在矩陣空間進行卷積，還將不同空間卷積的結果相加，通過注意力機制，將提取到的各類型信息進一步融合，最終進行分類，提高分類精度。

本文中提出的MAIF-GCN模型挖掘并融合了相鄰節點、同質型節點及共引型節點3種不同類型的關系節點，聚合了鄰接鄰居、同質最近鄰、共引最近鄰及三者組合的多角度的信息。在傳統社交網絡數據集上進行對比實驗，MAIF-GCN的分類精度比最先進的分類模型高，證明了提出的兩類型節點對社交網絡節點分類具有正向影響，證實了MAIF-GCN模型合理有效。