參照零模型的符號社會網絡嵌入性分析
李 紀,許小可
(大連民族大學 信息與通信工程學院, 遼寧 大連 116600)
0 引言
在現實世界的很多復雜網絡中,節點對之間存在著積極和消極2種關系,如朋友和敵人、合作和對抗、贊成和反對等[1-2]。若將這2種關系抽象為網絡連邊的符號屬性,讓正邊表示積極關系,負邊表示消極關系,這類具有正或負符號連邊的特殊網絡就被稱為符號網絡[3-4]。符號網絡的相關研究不僅可以為復雜社會系統的網絡演化、結構分析和動力學等提供豐富的理論依據,還可以為信息技術領域的個性化推薦、態度預測、用戶特征分析等提供實際的應用價值[5]。
在對符號網絡的研究中,通常需要考慮負邊信息的重要作用,并結合相關統計量來描述網絡的結構特征。例如,Kunegis等[6]提出使用節點的正負度之差來描述節點的相對重要性,使用聚類系數來描述網絡的凝聚性特征。由于不同的實證網絡在規模、類型和結構等方面具有較大差異,很多時候僅僅使用統計量的絕對數值對網絡結構特征進行定性或定量分析并不準確[7]。科學嚴謹的方法是引入該網絡隨機化后的零模型作為參照對象,基于統計性方法對比分析原始網絡和零模型網絡相同統計量的相對大小。例如,Maslov等[8]使用零模型作為參照對象研究蛋白質網絡拓撲結構的穩定性和特異性,這種研究方法對于符號網絡也具有很高的參考價值。
一個與實證網絡具有某些相同性質的隨機化網絡通常被稱為該實證網絡的隨機化副本,這類隨機化網絡在統計學上又被稱為零模型[9-11]。對于符號網絡零模型,最常見的是完全隨機置亂零模型和符號隨機置亂零模型。完全隨機置亂零模型是將原網絡的連邊符號和連邊位置都進行隨機化置亂,符號隨機置亂零模型只是隨機化置亂連邊符號,連邊位置保持不變。以上2種零模型均可在研究符號網絡結構特征時作為原始網絡的參照,與相關統計量結合就可準確分析出符號網絡的非平凡結構特征[12]。
“嵌入性”這一詞匯源自經濟學,在Granovetter[13]研究經濟行為與社會結構之間關系的文章中,對網絡嵌入性的概念做了較為全面的闡述。自此以后,嵌入性不論是在經濟學領域還是復雜網絡領域都得到廣泛的重視。在復雜網絡領域,針對符號社會網絡嵌入性的研究中,結構平衡理論提供了最基本的理論依據[14],像“朋友的朋友是我的朋友”這樣的推論已經成為了具有廣泛文化認同的格言。Leskovec等[3]利用共同鄰居節點數量來衡量節點對之間的嵌入水平,并驗證了嵌入水平高的節點對之間更有可能是正邊連接,該特性已被廣泛用于符號社會網絡的符號預測研究中。此外,Yuan等[15]和Wu等[16]都通過設置不同數值的嵌入水平,來檢測新提出的符號預測方法的性能。然而,針對大規模在線符號社會網絡的嵌入性特征分析結果并不全面,尤其是沒有結合零模型進行系統性分析。例如,Leskovec等[3]對符號社會網絡的嵌入性進行了初步分析,但其研究只分析了節點對之間的嵌入水平與正邊比例之間的關系,沒有探討負邊構成對于嵌入水平和網絡結構特征的影響。
為了更精確地分析正邊拓撲結構、負邊拓撲結構、連邊符號特征等對網絡嵌入性特征的影響,除使用經典的符號隨機置亂零模型和完全隨機置亂零模型外,又新提出3種更精細化的零模型:正邊隨機置亂零模型、負邊隨機置亂零模型和正負邊分別隨機置亂零模型,共5種零模型作為原始網絡的參照對象。結合本文中提出的正嵌入水平檢測統計量和負嵌入水平檢測統計量,分別對5個實證網絡的嵌入性進行分析。實證網絡分析結果表明,在符號社會網絡中存在:正嵌入水平越強,節點對之間的正邊比例越高;負嵌入水平越強,節點對之間的正邊比例越低的嵌入性特征。5種零模型分析結果顯示,前2種經典零模型的嵌入性特征與原始網絡有較大差異,而新提出的3種零模型卻與原始網絡具有相似的嵌入性特征。表明分別隨機化正邊或負邊拓撲結構,與獨立隨機化連邊符號對符號社會網絡的正負嵌入性特征的破壞是不同的。本文結論不僅有助于人們充分理解符號網絡嵌入性這類結構特征,還可以在符號預測和鏈接預測等方面發揮重要作用。
1 實證符號社會網絡數據集
本文中共使用了5個實證符號社會網絡數據集,分別是Bitcoin-Alpha、Bitcoin-OTC、Wiki-Rfa、Slashdot和Epinions符號網絡。其中Bitcoin-Alpha符號網絡和Bitcoin-OTC符號網絡都來自比特幣網上交易平臺,前者來自Alpha平臺[17],后者來自OTC平臺。在交易比特幣過程中,交易平臺為了防止普通用戶在不知情的情況下與劣質用戶之間進行交易,進而可能導致普通用戶利益受損,Alpha和OTC交易平臺都允許用戶之間相互標記為朋友和敵人關系,從而可以促成普通用戶多與優質用戶之間進行交易,并幫助普通用戶在交易時盡量躲避劣質用戶。
Wiki-Rfa符號網絡是一個維基百科管理員投票網絡[18]。維基百科在選取管理員時,每一位參與編輯維基百科的用戶都可以提出申請,成為維基百科管理員的候選人。后由候選人之間相互投贊成票和反對票,最后通過得票的多少選出新的管理員。Slashdot來自新聞網站Slashdot.com[3],Epinions來自符號網絡產品評論者網站Epinions.com[19-20]。這2個網站的用戶都可以發表自己的新聞或產品,并允許用戶間對各自新聞或產品給出喜歡或討厭的評價。
表1展示的是上述5個實證符號網絡的基本統計數據,包含節點總數、連邊總數、正邊比例和負邊比例。可以發現不同網絡的規模有較大差異,具體表現為節點和連邊總數從Bitcoin-Alpha網絡的幾千規模到Epinions網絡的幾十萬規模不等。基于該表也可以發現,所有實證符號社會網絡均表現出正邊比例遠高于負邊比例的統計情況。
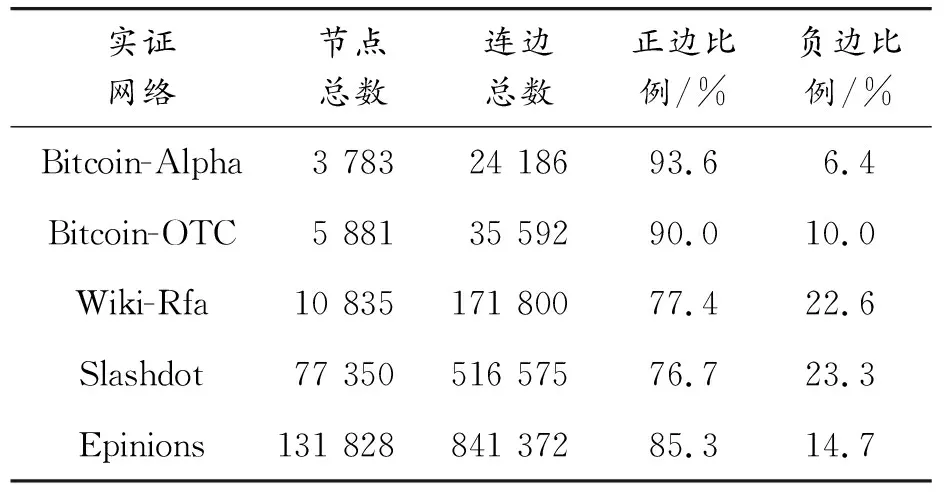
表1 實證符號社會網絡基本統計數據
2 符號網絡零模型的構造方法
復雜網絡零模型的構造方法主要有隨機置亂法和網絡模型法2種[21]。雖然網絡模型法構造的零模型有時可以很好地刻畫網絡的物理機制[22-23],但是在分析網絡內部更深層次的結構特征時,網絡模型法很難簡潔地構造出零模型作為參照,甚至很有可能無法構造出合適的零模型。隨機置亂法與網絡模型法的區別是,隨機置亂法并不是“從無到有”構造零模型,而是在原始網絡的基礎上,隨機化原始網絡的連邊位置或某些特定元素,簡潔地為原始網絡構造出合適的零模型作為參照。為了分析符號網絡內部更深層次的結構特征即嵌入性特征,使用的5種符號網絡零模型都是基于隨機置亂法構造的,分別是符號隨機置亂零模型、完全隨機置亂零模型、正邊隨機置亂零模型、負邊隨機置亂零模型和正負邊分別隨機置亂零模型。構造方法如圖1所示。前2種是在一般符號網絡中常用的零模型,后3種是新引入的零模型。
在圖1中,(a)表示一個擁有6個節點和7條邊的小型原始網絡,包含3條正邊(BC、DF、EF)和4條負邊(AB、AC、CD、DE);(b)表示原始網絡隨機置亂符號元素后形成的符號隨機置亂零模型。
符號隨機置亂零模型構造方法:在保持原始網絡連邊位置不變的基礎上,隨機選取一條正邊和一條負邊交換符號。例如將BC和DE交換符號,則BC變為負邊,DE變為正邊,就可以得到圖1(b)所示的符號隨機置亂零模型。需要注意,在構造符號隨機置亂零模型時,置亂符號僅限正邊和負邊之間,因為正邊與正邊、負邊與負邊之間置亂符號并不會讓原始網絡產生任何改變。
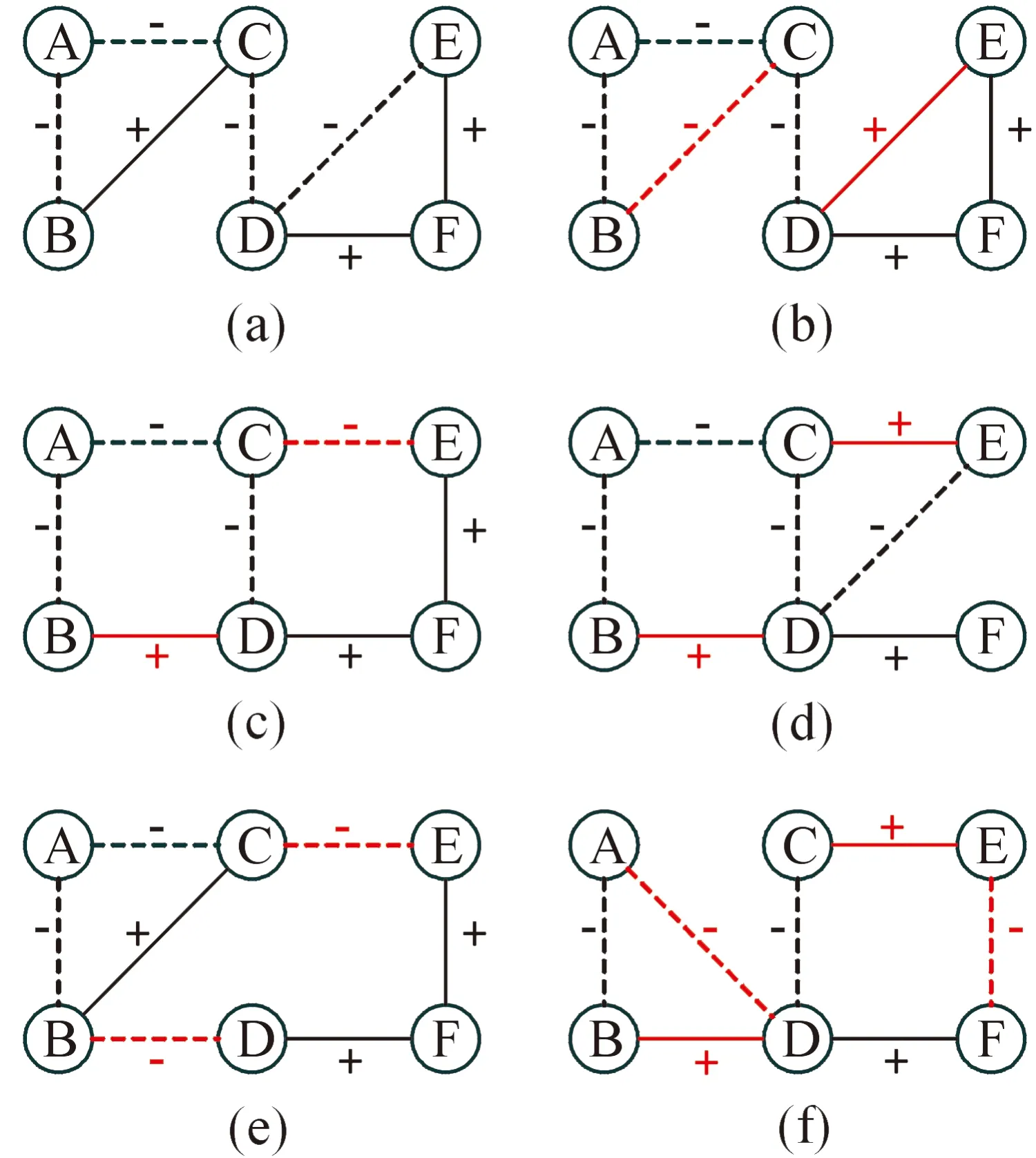
圖1 符號網絡5種零模型的構造方法
為更詳細展示符號隨機置亂零模型的構造過程,并將符號隨機置亂零模型構造方法運用到其算法中,設計如下偽代碼。其中布爾型變量result為成功置亂符號標記,整型變量nswap為成功置亂符號次數,整型變量max_tries為最大嘗試置亂符號次數。

符號隨機置亂零模型構造算法
輸入:原始網絡G,置亂次數N;
輸出:符號隨機置亂零模型。
方法:
result= False;
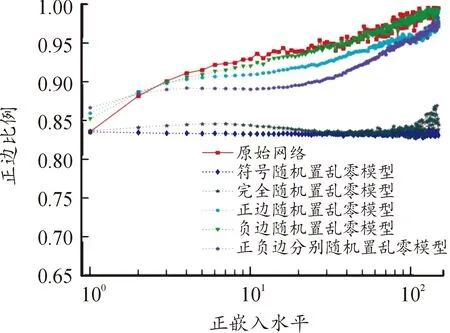
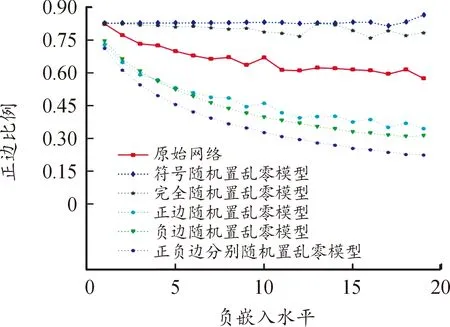
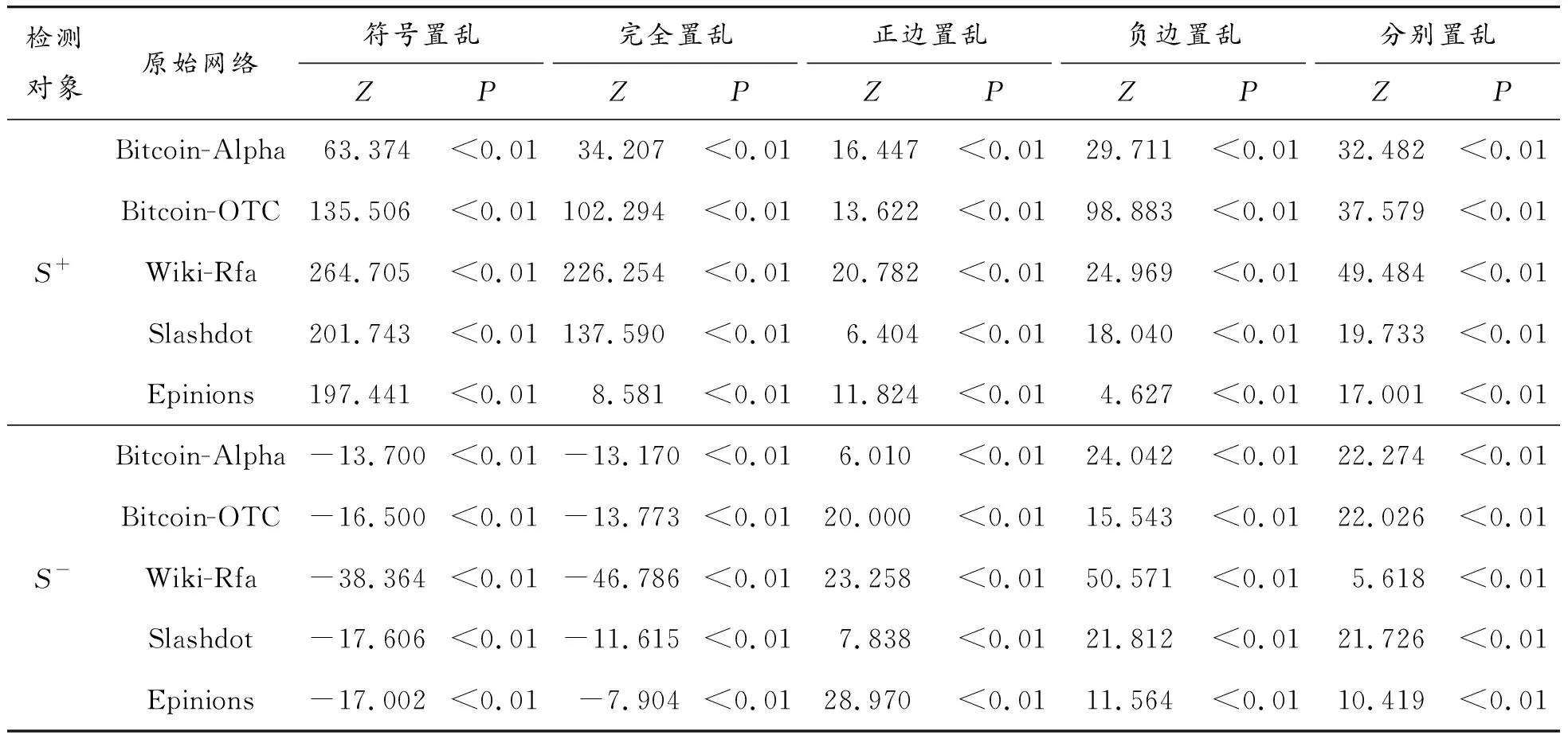
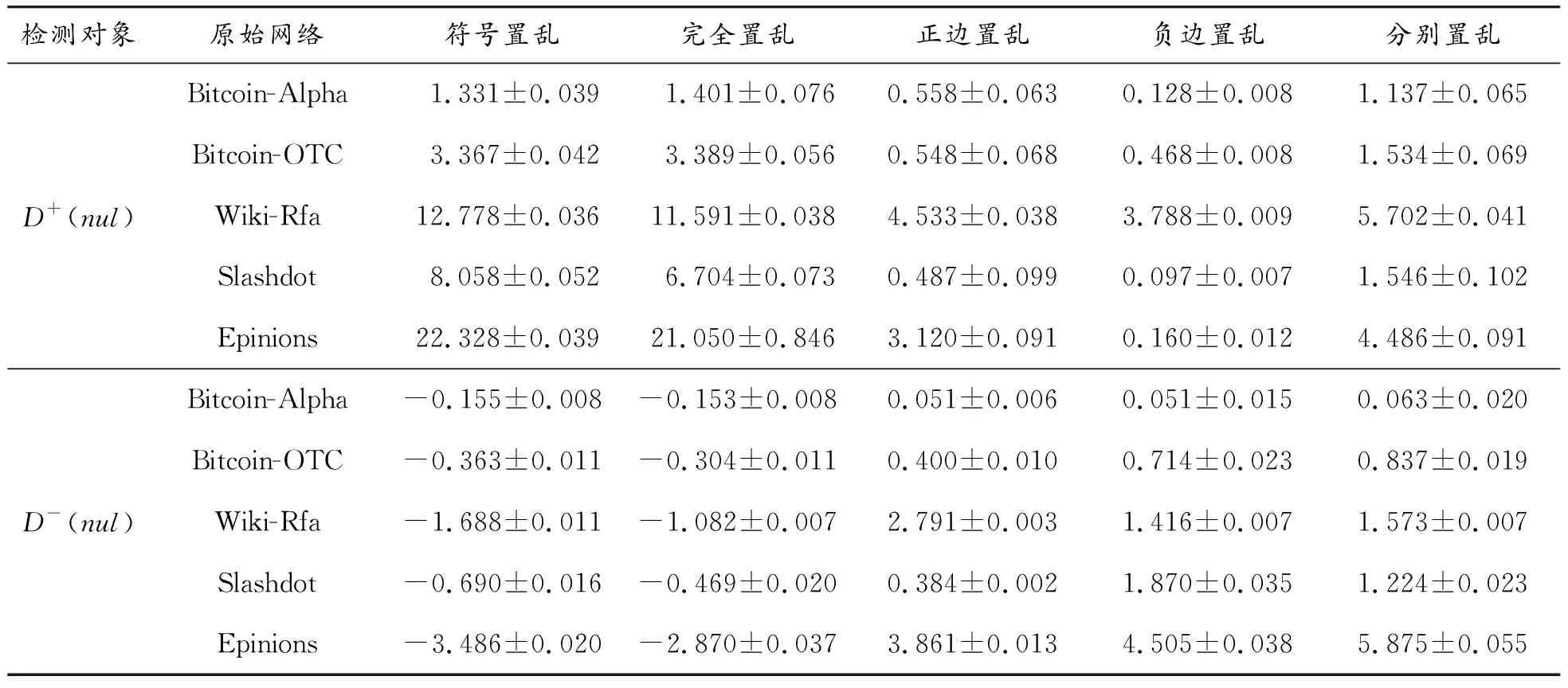
for (nswap= 0,max_tries= 0;nswap { 從G中隨機選擇2條邊em,n和ex,y; if (vm!=vn!=vx!=vy&&(em,n和ex,y的符號不同) ) 交換em,n和ex,y的符號; result= True; nswap++; endif max_tries++; if (max_tries> 5*N) result= False; break; end if } returnG 在圖1中,(c)—(f)都表示原始網絡隨機置亂連邊位置后形成的零模型。其中(c)是完全隨機置亂零模型、 (d)是正邊隨機置亂零模型、(e)是負邊隨機置亂零模型、(f)是正負邊分別隨機置亂零模型。它們的具體構造方法分別如下。 完全隨機置亂零模型構造方法:不考慮連邊的正負符號,只是隨機選取2條邊進行斷邊重連,并讓重連的2條新邊和斷開的2條原邊之間的符號保持不變。例如將BC和DE斷開,再重新連接成原始網絡中不存在的邊BD和CE,并讓BC和CE的符號相同,BD和DE的符號相同,就可以得到如圖1(c)所示的完全隨機置亂零模型。需要注意,由于完全隨機置亂零模型并不保證每個節點的正度值和負度值在置亂前后保持不變,因此隨機化程度在所有置亂連邊位置構造的零模型中是最高的。 正邊隨機置亂零模型構造方法:保持原始網絡的負邊連接關系不變,只是隨機選取2條正邊進行斷邊重連。例如將BC和EF斷開,再重新連接成原始網絡中不存在的正邊BD和CE,就可以得到如圖1(d)所示的正邊隨機置亂零模型。 負邊隨機置亂零模型構造方法:保持原始網絡的正邊連接關系不變,只是隨機選取2條負邊進行斷邊重連。例如將CD和DE斷開,再重新連接成原始網絡中不存在的負邊BD和CE,就可以得到如圖1(e)所示的負邊隨機置亂零模型。 正負邊分別隨機置亂零模型構造方法:若先對原始網絡進行正邊隨機置亂得到正邊隨機置亂零模型,再對正邊隨機置亂零模型進行負邊隨機置亂,就可以得到如圖1(f)所示的正負邊分別隨機置亂零模型。 需要注意,正邊隨機置亂零模型僅置亂了原始網絡的正邊拓撲結構,對負邊拓撲結構沒有影響,因此可以用來分析正邊拓撲結構對網絡結構特征的影響。同理,負邊隨機置亂零模型僅置亂了原始網絡的負邊拓撲結構,對正邊拓撲結構沒有影響,因此可以用來分析負邊拓撲結構對網絡結構特征的影響。正負邊分別隨機置亂零模型在構造過程中,正邊只和正邊置亂,負邊只和負邊置亂,并沒有進行正負邊之間的相互置亂。因此隨機化程度弱于完全隨機置亂零模型,但要強于正邊隨機置亂零模型和負邊隨機置亂零模型。 此外,需要說明的是,在圖1所示的零模型構造過程中,所有零模型都只進行了一次隨機置亂。若要生成足夠隨機化的零模型,實際實驗中都需要進行足夠多次數的重復置亂。在本文中,為了保證所有的零模型都足夠隨機化,設置的重復置亂次數都是原始網絡總邊數的5倍以上。 共同鄰居是目前最常用的檢測網絡嵌入水平的統計量。在無符號網絡中,共同鄰居對于檢測網絡的嵌入水平有著很好的效果。但在符號網絡中,忽略正邊和負邊的區別,直接使用共同正邊鄰居作為嵌入水平的檢測統計量,會造成負邊信息的全部損失。為充分利用符號網絡中特有的正邊和負邊信息,提出將符號網絡嵌入水平分為正嵌入水平和負嵌入水平兩類。其中正嵌入水平被用來分析正邊拓撲結構對符號網絡嵌入性的影響,負嵌入水平被用來分析負邊拓撲結構對符號網絡嵌入性的影響。 為了檢測符號網絡的正嵌入水平和負嵌入水平,對共同鄰居統計量進行改進,分別定義正嵌入水平檢測統計量和負嵌入水平檢測統計量。2個新統計量的公式為: (1) 在使用上述正嵌入水平檢測統計量,分析正邊拓撲結構對符號網絡嵌入性的影響時,可以繪制以正嵌入水平值為自變量,以該正嵌入水平值下節點對之間的正邊比例為因變量的函數曲線。函數公式為: (2) 式中:p+(k)表示正嵌入水平值為k的節點對之間的正邊比例;nk表示正嵌入水平值為k的節點對總數;mτ是一個常數,當第τ對節點對之間是正邊時,其值為1,否則為0。 同理,在使用負嵌入水平檢測統計量分析負邊拓撲結構對符號網絡嵌入性的影響時,可以繪制以負嵌入水平值為自變量,以該負嵌入水平值下節點對之間的正邊比例為因變量的函數曲線。函數公式為: p-(k)=1-p+(k) (3) 式中:p-(k)表示負嵌入水平值為k的節點對之間的正邊比例。 使用5種符號網絡零模型:符號隨機置亂零模型、完全隨機置亂零模型、正邊隨機置亂零模型、負邊隨機置亂零模型和正負邊分別隨機置亂零模型,共同作為原始網絡的參照對象。結合上文中提出的正嵌入水平檢測統計量和負嵌入水平檢測統計量,分別研究正邊拓撲結構、負邊拓撲結構、連邊符號特征等對符號網絡嵌入性特征的影響。 以Epinions符號網絡分析結果為例,其原網絡和5種零模型的p+(k)函數曲線如圖2所示。從圖2可以看出,隨著正嵌入水平的變化,節點之間存在連邊的比例是最高的,而且隨著嵌入性的增強存在連邊的比例也在增高。由于符號隨機置亂零模型和完全隨機置亂零模型中隨機化了不同連邊的依賴性,節點之間存在連邊的比例曲線都近似與X軸平行,說明這2個零模型中的一對節點之間是否存在連邊和網絡的正嵌入特征是無關的。剩余3種零模型的函數曲線與原網絡有著相同的上升趨勢,其中又以負邊隨機置亂零模型的上升趨勢與原網絡最為接近,但仍略低于原網絡。正邊隨機置亂零模型的上升趨勢略低于負邊隨機置亂零模型,完全隨機置亂零模型的上升趨勢在這3個零模型中是最低的。同時也需要注意,上述總結的函數曲線變化趨勢在較低的正嵌入水平值下并不顯著,甚至出現了相關的規律。 圖2 Epinions正嵌水平與正邊比例關系 不同零模型的函數曲線之所以表現出不同的變化趨勢,是由于相對于原網絡,5種零模型的隨機化程度不同。符號隨機置亂零模型和完全隨機置亂零模型在生成過程中,均完全打亂了原網絡的正邊相關性,因此看不出正邊拓撲結構對嵌入性的影響。剩余3種零模型,正邊隨機置亂零模型只是隨機化網絡的正邊拓撲結構,其負邊拓撲結構保持不變。負邊隨機置亂零模型只是隨機化網絡的負邊拓撲結構,其正邊拓撲結構保持不變。正負邊分別隨機置亂零模型只是分別隨機化網絡的正邊拓撲結構和負邊拓撲結構,并沒有讓正邊拓撲結構和負邊拓撲結構之間進行置亂。因此,剩余3種零模型的隨機化程度均低于符號隨機置亂零模型和完全隨機置亂零模型。在Epinions符號網絡中,負邊比例又明顯低于正邊比例,因此負邊隨機置亂零模型、正邊隨機置亂零模型和正負邊分別隨機置亂零模型的隨機化程度依次降低,它們的函數曲線上升趨勢也依次降低。 與分析正邊拓撲結構對符號網絡嵌入性的影響類似,同樣以Epinions符號網絡為例,展現負邊拓撲結構對符號網絡嵌入性的影響。其原網絡和5種零模型的p-(k)函數曲線如圖3所示。 從圖3可以看出,隨著負嵌入水平增強,原始網絡的一對節點之間的正邊比例降低,說明較強的負嵌入水平損害了節點對之間的正邊連接。符號隨機置亂零模型和完全隨機置亂零模型的函數曲線都近似與X軸平行,再次說明這2個零模型中的一對節點之間是否存在連邊和網絡的正嵌入特征是無關的。剩余3種零模型的函數曲線與原網絡有著相同的下降趨勢。但與分析正邊拓撲結構對符號網絡嵌入性的影響不同的是,這3種零模型的下降趨勢均強于原網絡,說明這幾種零模型對于網絡正嵌入性和負嵌入性的影響是不同的。 圖3 Epinions負嵌入水平與正邊比例關系圖 4.3.1量化分析指標 從定性上看,由于Bitcoin-Alpha、Bitcoin-OTC、Wiki-Rfa、Slashdot符號網絡的結果和Epinions在圖2、圖3中的結果是類似的,因此就不再一一展示。為了量化檢驗上述正邊拓撲結構和負邊拓撲結構對符號社會網絡嵌入性的影響模式,使用原始網絡的p+(k)和p-(k)函數值與不同零模型之差作為量化檢驗指標。2種檢驗指標的公式為: (4) 式中:D+(nul)指標被用來檢驗正邊拓撲結構對符號網絡嵌入性的影響模式;D-(nul)指標被用來檢驗負邊拓撲結構對符號網絡嵌入性的影響模式;S+(net)表示原始網絡的p+(k)函數與X軸差值累加;S+(nul)表示某種零模型的p+(k)函數與X軸差值累加;S-(net)表示原始網絡的p-(k)函數與X軸差值累加;S-(nul)表示某種零模型的p-(k)函數與X軸差值累加。式(4)中S+和S-計算公式都可以表示為: (5) 4.3.2嵌入性特征的統計檢驗分析 首先引入假設檢驗方法,分別推斷原始網絡S+(net)與零模型S+(nul)之間是否有顯著性差異、原始網絡S-(net)與零模型S-(nul)之間是否有顯著性差異。以S+為例(S-檢驗過程類似,因此不再敘述),可將原假設和備擇假設定為: H0:S+(net)=〈S+(nul)〉 H1:S+(net)≠〈S+(nul)〉 式中:〈S+(nul)〉為零模型S+(nul)的均值。可以構造差異檢驗統計量Z為: (6) 式中:σ+(nul)為零模型S+(nul)的標準差。 假設檢驗結果如表2所示,可以看出,所有P值均小于0.01,因此可以拒絕原假設H0,接受備擇假設H1。在統計學上說明原始網絡與5種零模型間的S+和S-均有顯著性的差異。為了進一步定量分析原始網絡與5種零模型間的差異程度,下面還需要使用D+(nul)和D-(nul)指標來衡量。 分別計算原網絡與5種零模型的D+(nul)和D-(nul)指標值,最終結果如表3所示。可見符號隨機置亂零模型和完全隨機置亂零模型的D+(nul)指標明顯大于另外3種零模型。說明符號隨機置亂零模型和完全隨機置亂零模型的p+(k)函數曲線與原網絡的相差較大,另外3種零模型與原網絡的相差較小。而在另外3種零模型中,呈現負邊隨機置亂零模型、正邊隨機置亂零模型和正負邊分別隨機置亂零模型的D+(nul)指標值依次升高,說明3種零模型的p+(k)函數曲線與原網絡的差異在依次增大。以上數據差異模式與Epinions符號網絡中正邊拓撲結構對符號網絡嵌入性的影響模式相符,從而可以說明,在本文使用的所有數據集中均存在與Epinions符號網絡相似的正邊嵌入性質。 同時,還可發現符號隨機置亂零模型和完全隨機置亂零模型的D-(nul)指標呈現負值,而另外3種零模型呈現正值。說明符號隨機置亂零模型和完全隨機置亂零模型的S-(nul)要大于原網絡的S-(net),因此它們的p-(k)函數曲線總體位于原網絡之上。新提出的3種零模型的S-(nul)要小于原網絡的S-(net),它們的p-(k)函數曲線總體位于原網絡的下方。以上差異模式基本與Epinions符號網絡中負邊拓撲結構對符號網絡嵌入性的影響模式相符,說明使用的所有符號網絡數據集中,均存在與Epinions符號網絡相似的負邊嵌入性質,也說明不同的零模型隨機化的拓撲結構性質對于網絡嵌入性的影響是不同的。 表2 實證符號網絡數據集假設檢驗結果 表3 實證符號網絡數據集量化分析結果 通過正嵌入水平下的節點對之間正邊比例函數,定性分析正邊拓撲結構對符號網絡嵌入性的影響,發現正嵌入水平越高的節點對之間正邊比例越高;通過負嵌入水平下的節點對之間正邊比例函數,定性分析負邊拓撲結構對符號網絡嵌入性的影響,發現負嵌入水平越高的節點對之間正邊比例越低。 符號隨機置亂零模型和完全隨機置亂零模型的嵌入性特征與原始網絡有較大差異,新提出的正邊隨機置亂零模型、負邊隨機置亂零模型和正負邊分別隨機置亂零模型卻與原始網絡具有相似的嵌入性特征。說明分別隨機化正邊或負邊拓撲結構,與獨立隨機化連邊符號對符號社會網絡的正負嵌入性特征的破壞是不同的。 使用零模型作為參照對象分析符號網絡嵌入性的方法還可以推廣到加權網絡、雙層網絡等其他類型網絡中,從而豐富網絡結構性質的研究方法庫。目前僅給出嵌入性檢測統計量來分析符號網絡的結構特性,分析角度有限,不足以全面刻畫符號網絡的結構性質,未來還可以引入更多的統計量,更全面地分析符號網絡的結構性質。
3 符號網絡嵌入水平統計量
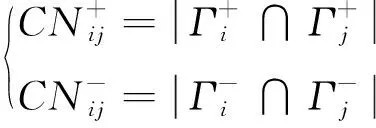
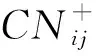
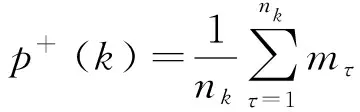
4 參照零模型的符號網絡嵌入性分析
4.1 正邊拓撲結構對符號網絡嵌入性的影響
4.2 負邊拓撲結構對符號網絡嵌入性的影響
4.3 參照零模型的嵌入性特征量化分析
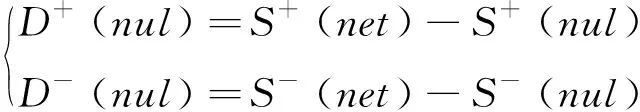
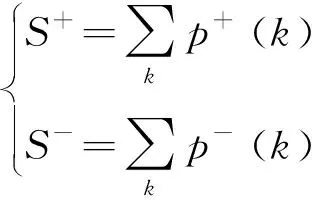
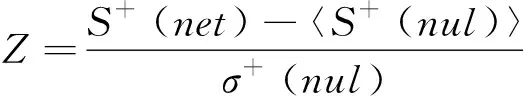
5 結論

