淺析七年級學生的負數(shù)學習困難與解決對策

謝小林

（重慶市巴南中學校，重慶 401320）

隨著負數(shù)概念的引入，七年級學生以前在自然數(shù)、分數(shù)和小數(shù)等數(shù)字學習中遇到的數(shù)學問題逐步得到解答，而負數(shù)的學習，不僅完善了數(shù)字的概念，也為下一步數(shù)軸的學習打下了基礎。然而負數(shù)的學習也給七年級學生帶了許多困擾，使他們在領會、理解、運用負數(shù)時出現(xiàn)比較多的數(shù)學錯誤，有的造成學生對數(shù)學學習的不良影響，以至嚴重影響到后繼的數(shù)學學習。對此，有必要分析其原因，提出數(shù)學教學的學習指導對策。

一、學生領會、理解、運用負數(shù)的困難

中國古代著名的數(shù)學專著《九章算術》最早提出負數(shù)運算法則，負數(shù)是指比正數(shù)與零都小的數(shù)，在生活中，負數(shù)代表與正數(shù)相反的數(shù)，如支出、減少、消費等內容，因此學習負數(shù)對學生更好地理解數(shù)學中的生活內容有重要的數(shù)學運用作用。然而，在中學數(shù)學教學過程中，學生領會、理解、運用負數(shù)時，表現(xiàn)出不同程度的障礙，如在“小王現(xiàn)在每個月的收入比以前增加了-522元”的實際問題中，學生對“增加了-522元”的出現(xiàn)感到不解，往往困惑于為什么增加了，增量卻是負數(shù)，認為每個月增加最少也應該是0元（即沒有增加）。實踐表明，學生領會、理解、運用負數(shù)的困難主要有以下幾種：

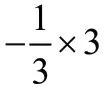
3.對數(shù)形結合時與負數(shù)有關的結論理解困難。七年學生在理解負數(shù)的相關結論時常常感到困難，例如，在負數(shù)大小比較時，對“絕對值越大的數(shù)反而小”不適應。尤其是在數(shù)形結合時，學生對“在數(shù)軸上原點左邊離原點越遠的點所表示的數(shù)反而越小”感到困惑。

4.數(shù)系擴充后對運算結果的考慮方式困難。由于負數(shù)的引入，在確定一個數(shù)時，我們要先定符號，再算絕對值。學生對這種新的考慮方式很不適應。尤其是七年級學習負數(shù)之初，學生常常在確定結果時，直接將符號問題撇開不管，只考慮絕對值部分；另一方面學生對有理數(shù)的加法法則、乘法法則、除法法則中關于符號的規(guī)定也不易理解。

5.解方程時存在移項易犯符號錯誤的困難。在解方程時，移項要變號，但是很多學生在移項時常常忘記變號。

6.對帶負號的式子的正負性判斷困難。比如有的學生面對式子“-a”的時候，始終認為這是一個負數(shù)。簡單的帶負號的式子理解起來是這樣，復雜的式子學生理解起來就更困難了。

7.負數(shù)認知活動中發(fā)現(xiàn)和理解情境中具有相反意義的量的困難。如用0表示參照標準和用負數(shù)表示參照標準兩端具有相反意義的量的困難，學生直線上的座位抽象出數(shù)軸表示的困難等。

二、學生領會、理解、運用負數(shù)困難的原因

1.前后認知沖突與思維定勢。《九章算術》最早提出的正負數(shù)加減法的法則是，正負數(shù)曰：同名相除，異名相益，正無入負之，負無入正之；其異名相除，同名相益。負數(shù)學習要求學生在概念、運算法則、運算律、與實際生活的聯(lián)系等方面進行重新構建，并與前兩個學段學過的數(shù)及其運算進行良好的對接。負數(shù)的出現(xiàn)突破了學生的原有認知：正數(shù)和負數(shù)表示具有相反意義的量，對0也需要重新認知：0不再僅僅表示沒有，它還是正數(shù)與負數(shù)的分界。學生的前后認知發(fā)生沖突，在心理上不能自然地接受負數(shù)概念的出現(xiàn)。同時受思維定勢的影響，學生在考慮問題時，仍然按照以前的思維方式和范圍來進行，常常只想到正數(shù)和0。比如當x2-4 ，求x的值時，學生往往想到的是+2，對-2的存在直接予以忽略。

2.學生受自身思維發(fā)展水平限制。七年級學生正處于從以具體形象思維成分為主向以抽象邏輯思維成分為主的轉折期，這種思維發(fā)展水平影響了學生在學習負數(shù)時做出正確的判斷，比如對前述式子“-a”的正負性的判斷，由于七年級學生的抽象邏輯思維能力相對較弱，他們往往習慣于所見即所得，認為式子“-a”的a前有一個“-”，所以就認為這是一個負數(shù)，對于“-a”的正負性依賴于a所代表的數(shù)的正負性，因這種認知比較抽象，所以一些思維發(fā)展水平較差的七年級學生便感覺難以理解，在做出判斷時犯錯的概率自然就增大了許多。

3.學生的學習習慣不好與學習方式不正確。一些學生養(yǎng)成了一些不良的學習習慣，對一些定義、定理、法則、公式的理解往往局限于背誦條文和模仿范例，而對其適用范圍、前提條件、具體要求往往選擇性忽略，缺少應有的思考；有的學生是因為上課聽講時的不良習慣和不正確的學習方式造成的，比如注意力不集中、不連續(xù)聽講，不看老師的板書、不動筆、只聽不練等；有的學生在書寫方面存在問題，例如，字跡潦草、書寫不規(guī)范。這些不良的學習習慣和方式也嚴重影響了學生對負數(shù)的學習。

4.負數(shù)學習本身的特點。歷史上人們對負數(shù)概念的接受經(jīng)歷了一個漫長的過程，負數(shù)概念給人們帶來了理解上的困難，如為什么“負負得正”，什么是“比沒有還要少”，甚至笛卡爾也認為負數(shù)是一個不合理的數(shù)。“-”號身兼三職：性質符號、運算符號、表示相反數(shù)，這雖然給數(shù)學學習和研究帶來了方便，但其產(chǎn)生的負面效應也不容小覷，尤其是負號與減號使用時的相互轉換，給學生的理解和運用帶來了很大的困難；當負數(shù)和相反數(shù)、絕對值、整式、去括號、一元一次方程等結合起來時，有的題目本身構成就顯得很復雜，需要較強的觀察、分析、計算、推理等多種能力，這些題目難度超出了學生能力范圍，使學生感到負數(shù)帶來的學習負擔之重。

5.教師教法和教學進度的安排。

（1）一些教師在處理涉及負數(shù)的問題時教法不當，給學生正確學習負數(shù)帶來阻礙。比如化簡式子3-2(3x-5)的過程中，對于2前面的“-”的處理，一些教師為訓練學生的發(fā)散性思維，一開始就介紹對2及其前面的“-”的不同處理，其中第一種做法是先把2前面的“-”當做減號，先用2與括號里面各項相乘，不急于去括號，然后再用去括號的法則去掉括號，第二種做法是將2前面的“-”當作性質符號，和2一起與括號里各項相乘從而去掉括號。這樣看似很科學的訓練方式卻造成學生頭腦里兩種解法糾纏不清；特別是第二種做法，學生要同時面對符號和絕對值的確定以及去括號法則的運用，這對學生的要求比較高，不少學生此時形成了認知混亂，出錯概率增大。

（2）教師在對學生進行訓練時提出了過高的要求。教師教學中提出的要求與學生的年齡特征和思維發(fā)展水平不相匹配，例如，在有理數(shù)的運算上，很多教師在學生接觸負數(shù)后不久，就在數(shù)字的復雜性、運算技巧、運算速度方面提出了過高的要求，許多學生在抽象思維能力相對薄弱的情況下被迫進入揠苗助長式的教學環(huán)境中，被弄得苦不堪言。

6.與數(shù)學相關的知識缺失。七年級學生因年齡相對較小，對外界事物接觸不多，對實際生活了解較少，這樣無形中造成他們對一些與數(shù)學相關的概念、專業(yè)術語不理解。比如對足球術語“凈勝球”，對股票術語“漲停、跌停”等，學生的認知缺失或不足導致他們對實際問題情境中哪些量具有相反意義并不理解，故而在運用數(shù)學知識解決問題時不能正確地運用正數(shù)和負數(shù)來表示相關的量或不能正確運用負數(shù)的相關規(guī)則進行運算、推理等。

7.學生數(shù)感、符號意識、觀察力薄弱以及畏難心理。七年級學生的數(shù)感、符號意識、觀察力沒有得到應有的發(fā)展，對負數(shù)的學習形成了一定的思維障礙和心理障礙，這些障礙不斷帶給學生挫敗感，造成學生無法順利建立學習自信，逐漸產(chǎn)生畏難心理，進而導致學生學習負數(shù)過程難以順利向前推進。

三、學生領會、理解、運用負數(shù)的有效方法

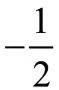
2.培養(yǎng)學生戰(zhàn)勝困難的意志品質和欣賞數(shù)學的心態(tài)。鼓勵學生戰(zhàn)勝負數(shù)帶來的困難。學習的過程，也是與困難進行較量的過程，優(yōu)良的意志品質對學生的學習帶來的促進十分重要。數(shù)學家杜賓斯基說過：“數(shù)學是困難的，不管用什么教學方法都無法改變這個事實。所以在數(shù)學的學習中，我們必須保持一種欣賞的心態(tài)來學習數(shù)學，只有這樣才能逐漸發(fā)現(xiàn)數(shù)學的美。”因此，對學生學習負數(shù)的心理和意志品質的培養(yǎng)也要給予足夠的重視，教師要運用自己的教學智慧，抓住七年級這個大好時機，培養(yǎng)學生對數(shù)學的欣賞心態(tài)和戰(zhàn)勝困難的意志品質，比如教師可以在課堂上介紹關于負數(shù)的相關數(shù)學故事，經(jīng)常表揚在負數(shù)學習時敢于戰(zhàn)勝困難的鮮活例子等。

3.教師在組織教學時循序漸進和遵循學生認知規(guī)律。教師在組織教學時，要循序漸進，遵循學生的認知規(guī)律。比如前文提到的化簡式子3-2(3x-5)的教學中，教師傳授的這兩種解法其實都沒錯，關鍵是傳授的時機不當。教師宜將第一種處理方式持續(xù)一段時間，待學生掌握得比較牢固后，再訓練學生采用第二種做法 ，這樣循序漸進、由簡到繁地推進教學進程，學生接受和掌握起來就容易多了。

4.充分利用數(shù)軸的形象直觀輔助學生對負數(shù)相關結論的理解。數(shù)形結合思想是非常重要的數(shù)學思想，數(shù)軸是數(shù)形結合的產(chǎn)物，借助數(shù)軸的形象直觀，可以有效地適應七年級學生當前的思維發(fā)展水平，加深對負數(shù)相關結論的理解，比如在理解-（-5）=+5時，可以讓學生利用數(shù)軸找出-5和+5在數(shù)軸上對應的點，直觀地體驗到這兩個點關于原點對稱，從而確信-5與+5互為相反數(shù)，而-5前面添上“-”也表示-5的相反數(shù)，所以自然得到-（-5）=+5。再比如，有的學生總是對兩個負數(shù)的大小比較有些認知模糊，教師不妨讓學生利用數(shù)軸來理解記憶，當遇到諸如-4.3和-3.4這種數(shù)的大小比較時，讓學生先習慣將這兩個數(shù)對應到數(shù)軸上，如圖：

然后在頭腦中形成-4.3對應的點在左，-3.4對應的點在右的具體形象，再根據(jù)數(shù)學規(guī)定，數(shù)軸上左邊的數(shù)小于右邊的數(shù)，這樣，學生對-4.3＜-3.4這個結論理解起來就容易許多。

5.放慢起始階段的教學進度。雖然七年級學生已經(jīng)在小學階段積累了一些數(shù)學基礎知識，但負數(shù)與他們從具體事物的數(shù)量中獲取的觀念并沒有共同點，他們正經(jīng)歷從具體數(shù)學向形式數(shù)學的第一次轉折，要想完全解決轉折中遇到的問題還需要高度的抽象能力，所以我們不能奢望七年級學生對負數(shù)的理解一蹴而就，教師此時需要耐心等待，當學生積累了大量的足夠多的經(jīng)驗后就會對負數(shù)逐步接受和理解。因此，教師在組織七年級學生學習負數(shù)時，一定要注意根據(jù)學生的掌握情況，放慢教學進度，留給學生足夠的消化和吸收時間。

6.充分發(fā)揮學習糾錯功能與榜樣示范引領。數(shù)學家杜賓斯基等人提出的APOS理論中提到以下教學理念：“要注意收集學生的想法、錯誤和成功之處，努力去理解他們。”所以基于這種教學理念，教師應在平時注意多收集學生在涉及負數(shù)的問題時常犯的錯誤，然后進行分類整理、剖析錯因；教師要采用換位思考的方式，矮化自己的思維水平，努力站在學生的角度去發(fā)現(xiàn)和思考他們在負數(shù)學習過程中遭遇的困境，然后思考切實有效的幫扶措施，進行及時的、針對性的、有效的強化訓練，將學生頭腦中的錯誤認知及時清除和改正過來，這樣做很關鍵，因為七年級作為初中學生的起始年級，他們對負數(shù)的掌握水平嚴重關切到后繼的數(shù)學學習興趣與學習自信。教師在處理學生學習負數(shù)暴露出來的負面情況的同時，也可收集自己任教班級中優(yōu)秀學生學習負數(shù)的成功經(jīng)驗，在學生中加以推廣，以榜樣示范引領，進行正向激勵，效果往往更好。

7.預判困難和提前防范。學生學習的過程也是一個不斷試錯的過程，作為教師，基于自身的教學素養(yǎng)，應對七年級學生學習負數(shù)時即將遭遇的困難做出預判，提前思考對策，防患于未然，比如教師可以在備課的過程中，結合自己學生的實際情況，充分思考學生在負數(shù)學習過程中即將犯錯的環(huán)節(jié)，教師提前在各個易錯環(huán)節(jié)上精心設計教案，在練習題的精選上下足功夫，提前預防，減少學生犯錯的概率，甚至讓學生不犯錯。

8.融合生活問題情境與引導學生關注社會生產(chǎn)生活。注意將生活中有關負數(shù)的問題情境融入平時的教學中，讓學生對負數(shù)知識日積月累，習以為常。同時，鼓勵學生多關注社會生產(chǎn)生活實際，增加閱歷，增強對現(xiàn)實生活的了解。這對學生的數(shù)學學習也是大有裨益的。