承上啟下，結好關鍵環——《認識千以內的數》教學設計

任霞

（江蘇省昆山市玉山鎮振華實驗小學，江蘇昆山 215300）

萬以內數的認識是小學階段數的認識教學中最重要、最關鍵的內容之一。一方面，我國的計數習慣是分級計數，萬以內的數是第一級（個級），學生掌握了萬以內數的計數單位、數位順序以及相鄰計數單位之間的進率，就能對十進制計數法形成正確而完整的認識，這也是進一步認識多位數的重要基礎。另一方面，萬以內數的順序、組成，數的讀寫方法，大小比較方法等都是整數認識中最基本、最重要的方法。千以內數的認識在這一學習序列中位處中間，是承上啟下的重要環節。

在學習本課內容之前，學生已經學習了“百以內數的認識”“百以內加、減法口算和筆算”“表內乘法和表內除法（二年級上冊）”，通過課前對學生的調查，發現學生對1 000以內數的認識并非零起步，大部分學生已經會讀、寫三位數，有部分學生已經知道10個100是1 000，這些都是學生學習本課的資源。

基于以上學情，把正確數出千以內的數，說出它們的組成，體會相鄰兩個計數單位之間的十進制關系作為本節課的重點，后者也是學生學習中最困難的地方。

帶著這些理解，筆者設計、執教了這節課，并取得了較好的教學效果。

【教學過程】

環節一：整理知識網絡，讓學生直觀感受到數數的方法及十進制的關系

學生雖然大部分都會數數，但大多都是零散的知識點，借助生活經驗的知識點，對于具體可以怎么數，如何選擇合適的方法數數沒有一個嚴謹的、科學的標準。從實物抽象到數字，數字又是怎么組成的？具體的數字又表示什么意思？數字與數字之間又有怎樣的關系？這些問題都需要老師一一幫學生理清，而不是單純的會數數，就結束了。因此，在教學前，選擇先帶著學生一起復習一下數數的方法，先一個一個數，滿十個，接著又可以十個十個數，滿一百個。從而引出，三百個小方框該如何數，學生自然而然就是想到要一百一百地數。

【片段1】

師：其實，除了這些比一百小的數，生活中還有很多比一百大的數，瞧，這臺電風扇的價格是300元，這個書包的價格是135元。這些數到底是怎么組成的？又該怎么數呢？今天我們就一起來認識千以內的數。（板書）

師：我們先從數小方塊開始，一個小方塊，1個一是一。接下來，我們跟著電腦老師一起數一數。

生：1，2，3，4，…，10。

師：這樣的一豎條表示10（板書）。

師：一個一個地數，10個1是10。（板書）

師：接著數。

生：10，20，30，…，100。

師：這樣的一板就表示100（板書）。

師：一百里面有幾個十呢？

生：10個。

師：一起來數一數，一十一十地數，10個十是一百。

師：這臺電風扇的價格300元，300個小方塊有多少呢？你打算幾個幾個地數？

生：一百一百地數。

師：那我們一起來數一數。

生：100，200，300。

師：一百一百地數，3個一百是三百。

環節二：借助工具，讓學生真正理解千以內數的組成。

二年級學生，抽象能力還是比較弱的，更多的需要借助工具，讓他們直觀地看到，這樣能更好地幫他們進行理解，教學中采用計數器和小方塊，讓學生更好地感知、感受數的組成，有助于學生了解千以內數的具體含義。直觀獲得的直接體驗能激發學生學習興趣，還能讓學生在過程中體會到成功，獲得學習的經驗。

【片段2】

師：討論：再搬來一個小方塊，一共有幾個了呢？你能用計數器來撥一撥、說一說嗎？

生情況1：直接把個位上9顆珠子退去，并在十位加1顆珠子（把滿十進一的想法放在了腦子里。）

師：你看懂他的做法是什么意思嗎。

生：他的意思就是個位滿十向十位進一。（板書：滿十進一。）

師：為了讓大家看得更明白一些，現在可以個位上撥10個，再全部后退，再在十位上撥一個。（邊說邊演示。）

生情況2：在個位上撥了10個珠子，再把他們全部退去，然后在十位上撥一個。

師：剛才他在個位上撥10個珠子，現在為什么要把他們全部退去，又在十位上撥了一個呢？

生：個位滿十，向十位進一。（板書：滿十進一。）

【片段3】

談話：你想嘗試一下在計數器上一邊撥珠子，一邊數數嗎？那我們就一起來動手、動嘴撥一撥、數一數。

出示要求：9個百（學生撥）問：在哪一位上撥了幾顆珠子？8個十（參照前面，交流反饋）。9個一。看一下，這個數是多少？

課件出示：一個一個地邊撥珠子邊數數。問：這次你打算在哪一位上撥珠子，每次撥幾顆？說說你的理由。明確：在個位上一顆一顆地撥珠子。

學生活動。交流，跟著電腦課件一起數。

師：和老師一起數一數。九百九十九里面有幾個百幾個十和幾個一？

師：九百九十九添上1是多少？先想一想，有困難可以小組討論一下。課件演示說明：九百九十九添上1是一千。

師追問：九百九十九添上1是多少？（九百九十九添上1是一千。）

師：同學們真了不起，認識了一個新的計數單位“千”，那么它在計數器上的位置呢？從右邊數，它是第幾位？

師：現在計數器上的這一顆珠子就表示一千。一千個小方塊有多少呢？你打算幾個幾個地數？一百一百地數，幾個一百是一千。（10個一百是一千。）

談話：現在掌握了幾種數數的方法，你覺得以后可以怎么數數？引導得出：數較少的數時，可以一個一個數，數較多的數時，可以十個十個地數，數更多數時，可以一百一百地數，如果小方塊的數量很多，我們還可以一千一千地數。

問：在計數器上，都能用1顆珠子來表示。看（點擊課件），這4顆珠子表示的意義一樣嗎？

師：我們在認數時，不僅要數對珠子的個數，還要看清珠子所在的數位。

環節三：在對比中發現規律，用規律來檢驗新知。

如何把學生零散的知識串成知識鏈，引導學生發現同類數之間的內在聯系，是本課設計過程中一直在思考的問題，常規的教學就是學完整百數，學幾百幾十幾，然后教學數的組成，一十一十地數，一個一個地數，最后數到一千，但這些，其實不上課，學生已經大部分都知道了，怎么在此基礎上突破，有沒有可以深挖的內容，基于以上的思考，有了如下的設計，分三個板塊，讓學生清楚認識整百數、幾百幾十、幾百幾十幾三類數的組成和數法。

【片段4】

認數整百數及整百數的組成。

過渡：剛才我們用三百個小方塊表示三百，聰明的小猴卻說，它只需要3顆珠子就行了。你知道它是怎么做的嗎？

師：你能在計數器上表示三百嗎？為什么百位上放3顆珠子就能表示三百呢？

師：這幾個計數器上表示的數你知道是多少嗎？說說你的理由。

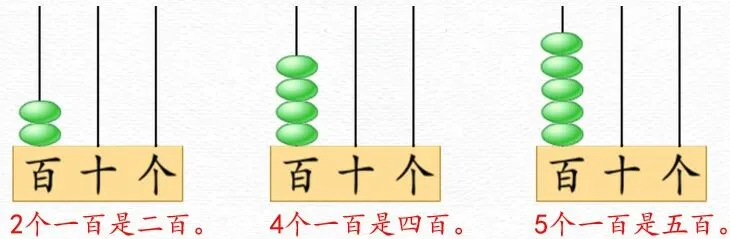
師：仔細觀察，你有什么發現嗎？（同桌討論。）

生：幾個一百是幾百。

【片段5】

認數幾百幾十幾及它們的組成。

這幅圖一共有幾個小方塊？你是怎么數的？（3個百，2個十和4個一，合起來是三百二十四。）

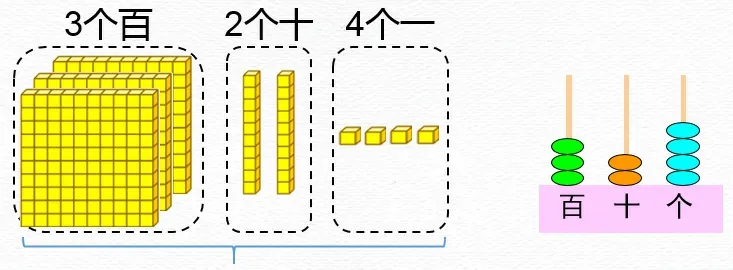
師：該怎么在計數器上撥出這個數呢？這些珠子分別表示什么意思呢？

鞏固訓練：

師：這幅圖中又有幾個小方塊呢？在計數器上該怎么撥？

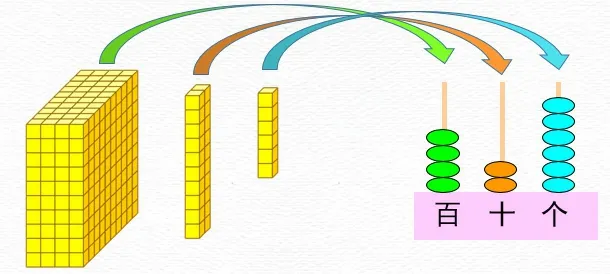
師：這幾個計數器上表示的數你知道是多少嗎？說說你的理由。

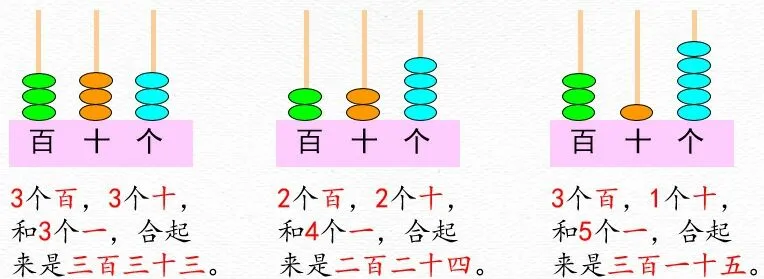
學生回答，并說說數的組成。

師：仔細觀察這幾個計數器上所表示的數，你有什么發現？

生：幾個百、幾個十和幾個一，合起來是幾百幾十幾。

【片段6】

認數幾百幾十及它們的組成。

這個計數器上表示的數是多少？（三百五十）誰能來介紹一下這個數？

出示要求：一十一十地數，該在哪一位上撥珠子？每次撥幾顆？說說你的理由。

明確：在十位上撥珠子，一顆一顆地撥表示一十一十地數。

師：跟著老師一起來數一數。

數到三百九十，追問，接下來是幾？說說你的理由？

明確：十位滿十，向百位進一。（板書：滿十進一）

師：沒有計數器，你也能一十一十地數一數嗎？

從七百六十數到八百三十。同桌互相數一數，指名數一數，集體數一數。

小結：從剛才的學習中，我們已經認識了幾百、幾百幾十、幾百幾十幾這些比一百大的數了。并且知道幾個一百是幾百；幾個百和幾個十合起來是幾百幾十；幾個百幾個十和幾個一合起來是幾百幾十幾。

環節四：及時鞏固練習，深化應用所學新知。

緊緊圍繞千以內數的意義這個重點，設計一內容豐富、層次鮮明、形式多樣的練習，引導學生通過具體的活動，進一步熟悉數數的方法，掌握數的組成，加深對數的順序和意義以及十進制計數法的認識，增強對數的實際大小的把握能力，重在培養學生的數感，發展學生的思維能力。

【片段7】

1.學生跟著課件一起數數

師：四百三十四，誰來介紹一下這個數，說說這個數的組成？

4個百，3個十，4個一合起來是四百三十四。

2.找規律填數

師：小方塊可以幫助我們數數，如果老師把小方塊拿掉，你還能數嗎？試試看。

師：你發現它的數數規律了嗎？

生：一百一百地數。（一十一十地數、一個一個地數。）

3.認一認，說組成

想想做做5

師：圖中有幾種面值的人民幣？你會統計它們各有多少張嗎？這些人民幣一共多少元？（）個百，（）個十，（）個一，合起來是多少？

生：指名學生回答。

師：一百三十五元，就是我們這個書包的價格。

想想做做6

師：你能看出這兩幅圖中有什么相同和不同的地方嗎？這兩個數分別表示的是多少？

生：四百七十，四百零七

師：這兩個數分別由4個幾和7個幾組成的？你能借助計數器完成嗎？學習單，想想做做6。獨立完成。

為什么這里的7表示的是7個十，而這里的7卻表示7個一呢？

生：7在十位上，表示7個十，7在個位上，表示7個一。

4.猜一猜

師：今天，小朋友們的表現真不錯，接下來我們進入游戲環節，放松一下，猜一猜。

（1）八百零一

我擺的數在七百八十六到八百零五之間。學生猜。根據學生猜測提示大小。

（2）一千

我擺的數是我目前認識最大的數。

猜猜我在計數器上是怎么擺的。千位放一顆，百位放10顆。

師：為什么兩種都能表示一千。

（五顆珠子擺一個三位數）

我擺的數比一千小，比一百大。任意猜。我擺的數用了5顆珠子。

生再猜。你敢挑戰獅子王，用5顆珠子擺出不同的三位數嗎？生嘗試在計數器上撥一撥。

師指名上臺交流匯報。適當分散教學難點，加強認數的直觀性，突出對數的意義的理解精心選擇學習素材，讓學生聯系生活實際認識千以內的數。這樣的一個設計旨在結好整個認數過程中的關鍵環，讓學生能夠利用本課所學的經驗，去更好地學習接下來的內容，用今天的方法去解決明天的難題，培養學生的數感、培養學生的數學思維，授之以魚不如授之以漁。