由描述性到形式化：中學函數定義的發展及其價值

劉 杰，韓繼偉，高 夯

由描述性到形式化：中學函數定義的發展及其價值

劉 杰，韓繼偉，高 夯

（東北師范大學 數學與統計學院，吉林 長春 130024）

函數概念是貫穿于初、高中數學教學的主線之一，兩學段教材中函數概念的定義內容發生了本質的變化．在對初、高中數學教材中的函數定義內容的異同點進行比較的基礎上，分析了從初中函數概念到高中函數概念發展的學科價值和教育價值，以及中學數學教材處理函數概念的合理性，并提出當前教材在兩個函數的相等和大小問題上仍存在值得討論的問題．

函數概念；對應關系；教材分析；中學數學

函數是數學的核心概念之一，更是貫穿初、高中數學的一條重要主線，但由于其內容的高度抽象性和復雜性，函數概念常常被視為中學數學中最難教和最難學的概念之一[1]．

函數概念是中學數學中少有的在初、高中階段均給出明確定義的數學概念，但對比兩個學段教材中給出的定義，將不難發現兩者之間存在著本質的不同，函數概念的定義由初中到高中的發展經歷了數學抽象水平不斷加深的過程[2]．但在實際教學中，兩個定義的差異似乎并未引起廣大師生的注意，例如有研究發現，當問及高中生函數概念的定義時，被試學生給出的各種答案中占比最多的仍是初中階段學習的定義內容[3]；當問及教師初、高中教材中的兩個函數定義的區別時，受訪教師中竟有很大一部分高中教師無法說清兩個定義的本質區別是什么[4]．由此可見為實現初、高中函數概念教與學的有效銜接，將十分有必要對中學函數概念的發展問題做出澄清．

盡管當前有關函數概念的歷史演變、教材設計、概念教學以及學生認知水平等方面多有研究[5–9]，也有研究者就初、高中函數知識的教學銜接問題展開了討論[2]，但針對初、高中函數概念定義內容的發展問題的分析卻少有涉及．因此，這里以人教版初中和高中數學教材為例，分析初、高中函數定義的發展特征以及函數定義發展的學科價值和教育價值，并對當前數學教材函數內容的處理展開進一步的討論，為中學函數內容的教學提供借鑒．

1 中學函數定義的發展

由初、高中函數概念的定義內容可見，中學函數定義的發展既有階段性也有連續性，階段性表現在函數定義的發展經歷了初中的描述性定義和高中的形式化定義兩個階段．連續性則表現在函數概念的描述性定義是形式化定義的基礎，從初中到高中，函數定義的抽象水平不斷加深．下面以人教版教材（由于中國的教材編制采取“一綱多本”的原則，目前使用的版本數量較多，但整體而言人教版、北師大版等版本的適用范圍較廣[10]，因此選擇適用范圍最廣的人教版數學教材為例進行分析）中所呈現的內容為例，來分析初、高中函數概念的發展．教材中有關函數概念的定義被安排在初中的八年級下冊和高中的數學必修1（A版）．

1.1 函數的描述性定義

直觀的自然語言表示、符號語言表示和公理化語言表示是中學數學概念的3種表示方式[11]，而用簡明、直觀的自然語言對數學概念的本質屬性進行描述的定義方式可稱為數學概念的描述性定義．

人教版八年級下冊數學教材中給出的函數概念的定義如下：

函數概念的本質屬性是元素與元素之間的對應[12]，這個定義用簡單清晰的自然語言直觀地描述出了函數概念的本質屬性，因此可將初中教材中給出的函數概念的定義視為函數的描述性定義．

1.2 函數的形式化定義

中學數學的形式化主要表現在數學符號的運用[11]，相應地，數學概念的形式化主要表現為對概念結構的符號表達．而用符號化語言對數學概念的本質屬性進行描述的定義方式可稱為數學概念的形式化定義．

人教版高中數學必修1（A版）數學教材中給出的函數概念的定義如下：

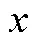
這個定義抽象出了函數的對應關系，并用符號化的語言對函數概念進行定義，因此可將高中教材中給出的函數概念的定義視為函數的形式化定義．

1.3 描述性定義與形式化定義的區別

由定義內容來看，初中的描述性定義是基于變量的依賴關系，定義內容強調的是用函數描述一個變化過程[13]．而高中的形式化定義則是基于集合間的對應，定義內容強調的是用函數描述一種對應關系或者是一個變化結果．

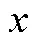
為使表達簡潔方便，下文將初中教材給出的函數概念描述性定義和高中教材給出的函數概念形式化定義分別簡稱為定義1和定義2．

2 函數由描述性定義到形式化定義的學科價值

2.1 形式化定義嚴格刻畫了函數的性質

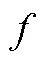
表1 初中和高中數學教材中函數單調性描述

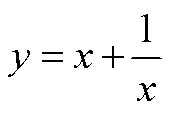
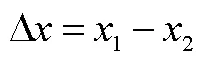
因此高中函數單調性的描述是基于推理和運算的，使定義1意義下的性質描述所產生的問題得以克服．數學教材中的函數概念由定義1向定義2的發展，使函數的性質得以嚴格的形式化表達，這是后續數學發展的基礎．

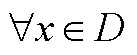
2.2 形式化定義擴充了函數研究的范圍

2.3 形式化定義改變了函數研究的方法

函數概念由定義1向定義2的發展不僅擴大了函數研究的范圍，函數研究的方法也得以拓展．初中研究函數的方法只能通過“描點作圖”先畫出函數圖象再根據圖象進行函數性質的分析，而高中對函數的研究不再局限于根據圖象分析性質這一條研究路徑，還可以先分析函數的性質再借助性質分析圖象，或者性質與圖象交互分析．

表2 高中數學教材中研究三角函數的方法

3 函數由描述性定義到形式化定義的教育價值

3.1 形式化定義有利于培養學生的抽象能力

抽象是數學學科的本質特征和數學學習的思維基礎，幾乎所有學科都離不開抽象，但抽象的價值在數學中表現得尤為淋漓盡致．抽象是個體在心理層面上從特定角度構建對象之間關系的過程[14]，學生的抽象能力與數學學業成績存在密切的聯系[15]，精通數學的學生必須具備較高的抽象能力，因此培養學生的數學抽象能力是提高學生學業成績和發展學生學科素養的重要舉措．

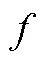
3.2 形式化定義有利于提高學生的數學建模能力

數學模型是數學應用的重要表現形式，通過數學模型使現實與數學這兩個不同的世界得以關聯[13]．所謂建模簡而言之就是用數學的方法解決實際問題，實現由現實進入到數學最終再回到現實的過程．經歷數學建模的過程能夠讓學生體會如何用數學的眼光觀察世界，如何用數學的思維思考世界以及如何用數學的語言表達世界，提升學生的數學素養[17]，因此培養學生的數學建模能力是數學教育的重要任務之一．盡管在不同研究中數學建模被賦予不同內涵，但無論是在建模過程的“四階段”“五階段”還是“七階段”劃分中[18]，建立數學模型始終是建模活動的關鍵環節，其本質特征便是從復雜的問題情境中抽取出相關變量并建立起變量間的函數關系．

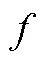
3.3 形式化定義有利于增強學生的數學運算能力

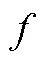
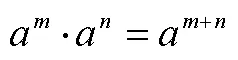
4 討論

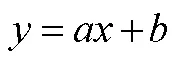
數學學科核心素養的養成是數學知識與思維相融合的結果[22]，有關初、高中數學教材對函數定義的設置問題，在初中教材中給出描述性定義的基礎上在高中階段進一步給出抽象水平更高的形式化定義，無論在數學學科教學還是數學核心素養培育上均具有重要意義．但不可否認的是，現行教材在函數概念的處理上仍存在幾點值得進一步討論與思考的地方．

[1] 史寧中，濮安山．中學數學課程與教學中的函數及其思想——數學教育熱點問題系列訪談錄之三[J]．課程·教材·教法，2007，27（4）：36–40．

[2] 鄧勤．新課程背景下初高中數學教學的有效銜接——從函數概念的教學談起[J]．數學通報，2011，50（2）：33–35．

[3] 任明俊，汪曉勤．中學生對函數概念的理解——歷史相似性初探[J]．數學教育學報，2007，16（4）：84–87．

[4] 林玉慈，史寧中．高中生對函數的認識與態度[J]．東北師大學報（哲學社會科學版），2018（3）：186–191．

[5] 劉思璐，沈中宇，汪曉勤．英美早期代數教科書中的函數概念[J]．數學教育學報，2021，30（4）：55–62．

[6] 呂世虎，王尚志．高中數學新課程中函數設計思路及其教學[J]．課程·教材·教法，2008，28（2）：49–52，86．

[7] 李吉寶．有關函數概念教學的若干問題[J]．數學教育學報，2003，12（2）：95–98．

[8] 賈隨軍．函數概念的演變及其對高中函數教學的啟示[J]．課程·教材·教法，2008，28（7）：49–52，72．

[9] 朱文芳，林崇德．初中生函數概念發展的特點[J]．心理科學，2000（5）：517–521，636．

[10] 胡典順．國際數學教育比較研究[M]．武漢：華中師范大學出版社，2016：145．

[11] 張奠宙，過伯祥．數學方法論稿 [M]．修訂版．上海：上海教育出版社，2012：86–91，93．

[12] 李祎，曹益華．函數概念的本質與定義方式探究[J]．數學教育學報，2013，22（6）：5–8．

[13] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2018：6–7，109，116–118．

[14] van OERS B, POLAND M. Schematising activities as a means for encouraging young children to think abstractly [J]. Mathematics Education Research Journal, 2007 (2): 10–22.

[15] SCHLEY D R, FUJITA K. Seeing the math in the story: On how abstraction promotes performance on mathematical word problems [J]. Social Psychological and Personality Science, 2014, 5 (8): 953–961.

[16] 王欽敏，余明芳．數學思維素養深度涵育：教學的進路與方略[J]．數學教育學報，2020，29（6）：56–60．

[17] 史寧中．數學思想18講[M]．北京：北京師范大學出版社，2016：14，218．

[18] 黃健，魯小莉，王鴦雨，等．20世紀以來中國數學課程標準中數學建模內涵的發展[J]．數學教育學報，2019，28（3）：18–23，41．

[19] 李敏，嚴忠權，莫曉輝．核心素養視域下對數學思想方法的思考——以函數為例[J]．教育觀察，2020，9（43）：56–59．

[20] 中華人民共和國教育部．義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2012：13．

[21] 沙振舜，鐘偉．簡明物理學史[M]．南京：南京大學出版社，2015：22–27．

[22] 武麗莎，朱立明．高中數學學科核心素養：生成機制與培養路徑[J]．數學教育學報，2021，30（4）：25–29．

From Descriptive to Formal: The Development of Middle Schools’ Function Definition and Its Value

LIU Jie, HAN Ji-wei, GAO Hang

(School of Mathematics and Statistics, Northeast Normal University, Jilin Changchun 130024, China)

Function concept is one of the main lines running through the mathematics teaching in middle and high schools. The definition of function concept in the textbooks for the two levels of schooling has undergone essential changes. On the basis of comparing the similarities and differences of the function concept’s definition in mathematics textbooks for middle and high schools, this paper analyzes the subject value and educational value of function concept’s development from middle schools to high schools and presents the rationality of processing function concept in mathematics textbooks for middle and high schools. This study also points out that there are still some problems worth discussing in the current textbooks on the equality and magnitude of the two functions.

function concept; corresponding relationship; textbook analysis; middle school mathematics

2022–02–13

2021 年度吉林省社會科學基金項目——教師評價素養的發展研究（2021B152）

劉杰（1992—），女，山東日照人，博士生，主要從事數學教育研究．

G632

A

1004–9894（2022）03–0001–05

劉杰，韓繼偉，高夯．由描述性到形式化：中學函數定義的發展及其價值[J]．數學教育學報，2022，31（3）：1-5．

[責任編校：周學智、陳漢君]