操作延展性練習教學——在兩種推理交互作用中發展數學新知識

顧麗英，鄧德巍

操作延展性練習教學——在兩種推理交互作用中發展數學新知識

顧麗英1，鄧德巍2

（1．無錫市新洲小學，江蘇 無錫 214112；2．淮安市洪澤實驗小學，江蘇 淮安 223100）

在宏觀背景和教育大環境相對不變的情況下，改進教學方法是提高教學質量的根本措施．各種教學方法層出不窮，其種類和定義也更加具體確切，更加專業．延展性教學就是一種．延展性是源于物質的一種物理屬性，指可錘煉可壓延的程度，這里把它擬人化地用于數學教學，以錘煉一個人的數學品質與能力，借以高標準地提高學生的數學核心素養．在回顧與分析這種教學方法的特點與模式之后，把它納入到認知心理學及教育學研究的“三象一作”數學認知過程，由無錫市新洲小學等學校展開延展性練習教學．教師精心設計教學過程，通過一些典型教例，把“語言傳遞、直接感知、實際訓練、引導探究、活動欣賞”等幾種常用方法融為一體，在合情推理與演繹推理交互作用中延伸與拓展數學思維活動，發展數學知識．通過統計分析，學生數學推理能力有顯著提高．實踐證明數學課堂的延展性教學這種教學方法在小學數學教學中是可行的和有效的．其努力方向是：針對不同學生的認知基礎和認識方式的差異，教學設計中還必須為學生提供和呈現多樣化策略的應用與選擇．延展性教學的進一步詮釋過程中，對數學教學的終極目標也作了一點思考．

“三象一作”過程；延展性練習教學；合情推理能力；邏輯推理能力；終極目標

1 問題提出

隨著現代學校教育教學理論和實踐的不斷深入與發展，人們對教學方法本質的研究趨于深刻，各種教學方法層出不窮，對教學方法的種類和定義也更加具體、確切，更加專業．其總目標都是為了提高教學效率[1]．因為教學的時間是固定和有限的，因此改進教學方法，調動學生好學上進的積極性，就是提高教學質量的根本措施．教學方法多種多樣，其性能和特點千姿百態．在實際教學時，教師能否正確選擇教學方法，就成為影響教學質量的關鍵問題之一．實踐證明，教師只有按照一定的科學規律，綜合考慮教學的各種因素，選擇適當的教學方法，并能合理地加以組合，才能使教學效果達到最優化的境地．延展性教學就是一種合理的新的教學方法與教學模式．依據“科學教育學之父”赫爾巴特的主張，在延展性教學中把學生的個性作為出發點，培養學生多方面的興趣作為終極教學目的的最近教學目標，使課堂教學作為經驗與交際的補充，關注學生“與教學相合拍的心理狀態”等．認為興趣標志著學生智力活動的特性，它可以通過教學激起，進而促進學生觀念體系的完善[2]．

近年來也有一些中小學在數學教學中開始研究與應用延展性教學方法，其中包括把數學知識與技能向課內與課外的延展等．“有效延展，促進內化”指出知識只有內化為學生自己的才是穩定的、有效的，為了促進知識內化，教學就不能灌輸，不能孤立地講解知識點，而應該注重知識的延展性．數學教師應根據不同的學習內容目標和學生的實際情況，給學生留下延伸拓展的空間、時間，指導學生獨自去思考、探究，從而培養學生的探究、創新能力．延展性教學對發展學生的數學素養，提升學生能力提出了具體要求，同時，也對廣大一線數學教師如何實施有效教學，提升學生能力方面指明了方向[3]．有2篇文獻主要介紹了小學數學教學中對延展性問題的思考．其做法是：一是延伸和拓展有價值的問題，其方法有反向提問法、條件演變法、操作驗證法、推廣變式法和知識遷移法等；二是關注課本習題，引導學生主動探究，延伸課本習題，組織學生交流經驗，拓展課本習題，鼓勵學生靈活運用，使“教·學·做合一”的思想真正落到實處[4–5]．

作為小數教材中任何一個章節的知識與內容本身具有延展性，它們都是整個數學科學知識系統中的一部分，它在客觀上都包含有比教學大綱規定要學習的多得多的數學思想和方法．但有時人們過分強調可接受性原則．教師不愿意其實是不善于把它納入某一知識系統中去考察．其實，就教學的可接受性原則而論，它也應包括3個方面：傳授的新知識應對學生現有的知識、以他們的生活經驗為基礎；學習的知識系統應有助于向更高的一般發展水平過渡，或為這種過渡造成明顯的趨勢；在具體的教學條件下，某一內容對于完成學生發展任務的必要性，應當是顯而易見的．例如，“用計算器探索規律”（課標蘇教版第八冊83–84頁）．借助計算器，探索并掌握“一個因數不變，另一個因數乘幾，積也隨著乘幾”的變化規律．通過實踐教學，許多老師都覺得這一課的內容比較單薄．發現在一節課內進行教學和相應的應用練習，時間還有多余，學生也似乎還有學習的余力．故對其進行了拓展延伸，教師可以有多種處理方式，比如增加練習，進而鞏固知識；又如適當地補充學習內容：（1）一個因數不變，另一個因數除以幾時商的變化；（2）兩個因數都有變化時積的相應變化，等等．從而拓展學生的數學思維，培養學生的數學能力．當然，這是對學有余力的同學而言．對于一般學生則可在今后的學習和練習中慢慢鞏固．這樣做不但有利于學生的發展和提高，還能有效地避免學生產生思維定勢．這是一個關于數學知識延展性教學的具體例子[6]．

這里所要研究的問題是基于這2個文獻．一是文獻[2]指出，教學中的首要任務是開拓學生的思路，培養學生正確的思維方式，讓學生盡快由形象思維方式轉換為抽象思維加邏輯思維的方式．以形態理解和想象為中心展開練習，旨在拓寬學生的思路和提升思維質量．同時，由于人類的思維方式和行為方式隨著社會的發展在不斷發生變化，一些曾被視為對立的概念諸如抽象與形象、感性與理性思維的方式，現在看來正變得融合和統一．在這樣的背景下，讓學生以靈活、新穎的方式和多維的角度探求事物運動內部機理的思維活動和知識構架、整體把握能力的培養就顯得特別有意義．通過綜合訓練使學生盡量能達到在遇到新的問題或情況時，會選擇解決問題的恰當辦法．長期的教學實踐證明，心象構成與抽象構成的相輔相成可以使學生進一步理解數學概念的基本內涵．

二是文獻“論一種緣自認知心理學及教育學研究的數學認知過程”．王名揚等提出了一種全新的教學認知過程——“三象一作”模式，即“數學現象、數學心象、數學抽象、操作階段”．這個模式指出：人們想獲得高度總結性的科學知識，一般來說總是要經歷數學現象→數學心象→數學抽象這樣的認知過程．但認知過程中還包含一個重要的階段，即“操作階段”．這是一個在對知識不斷運用和不斷認知中再提升的階段．具體來說“就是在合乎邏輯法則的條件上操作運用抽象的數學知識與數學方法（包括數學符號及語言）去處理數學問題，并進一步發展數學理論知識”[7]．

【研究問題】基于上述兩個文獻，并借鑒前面延展性教學的有關理論與實踐，學校組織教師在小學數學教學中進行操作延展性練習教學的探析研究活動，著重從“數學的現象到數學的心象，再到數學的抽象”的可操作階段中展開，使直覺、形象思維與邏輯、抽象思維，也即合情推理與演繹推理（下簡稱形象思維與抽象思維）這兩種推理交互作用發展數學新知識．把數學教學過程中的“語言傳遞、直接感知、實際訓練、引導探究、活動欣賞”等幾種常用方法融為一體．

2 形象思維與抽象思維交互作用發展數學新知識的延展性練習教學

其實所謂延展性是指物質的一種物理屬性，指可錘煉可壓延程度．易鍛物質不需退火可錘煉可壓延．可鍛物質，則需退火進行錘煉和壓延．脆性物質則在錘煉后壓延程度顯得較差．物體在外力作用下能延伸成細絲而不斷裂的性質叫延性，在外力（錘擊或滾軋）作用能碾成薄片而不破裂的性質叫展性．延展性也可形容一個人的品質與能力，某人延展性強是指他可塑性強，可以勝任多種角色或者多個工種．下面，嘗試給出延展性教學的一個界定，因為這里所感興趣的是數學教學的延展性．

首先指出，數學教學過程，是學生在教師的指導下通過自己的思維活動，學習數學知識、數學規律和數學思想方法，并不斷自我增進數學素養的過程．

【延展性數學教學的界定】所謂延展性數學教學，就是指對數學教學過程進行延伸與拓展的教學（內涵）．推廣、擴充或遷移數學知識，培養和發展學生的創造性思維能力，獲得廣闊的思維空間，找到新的方法與觀點，更好地解決數學問題，發展數學新知識．教學中，教師全面揭示數學思維過程，可能與必要時把數學思維活動過程的慢鏡頭展現出來，啟迪和發展學生思維，將知識發生、發展過程與學生認知的生理心理活動統一起來．把數學教學過程打造或錘煉成學生身心健康發展的良好的運動場（外延）．

推理是數學的基本思維方式．推理一般包括合情推理和演繹推理．合情推理是一種創造的思維活動，演繹推理是一種收斂的思維活動．以兩種推理互補應用到數學新知識的發展主要是指在“三象一作”的操作階段中，如何讓學生在交互應用演繹推理和合情推理兩種推理方式中，做到有機結合、相輔相成、優勢互補、相得益彰，從而去解決數學問題，并發展數學新知識的一種操作過程．

因為人腦是具有抽象本能的，但它需要通過不斷訓練逐步喚醒和增長這種抽象能力．所以在這一過程中，首先是運用性推理的奠基，是學生基于某一種問題，運用數學知識及方法進行推理活動，從而獲得問題解決．這一抽象水平是學生在操作階段進一步抽象發展的起點，沒有這樣的基礎性保證，進一步的抽象發展將成為無本之木，無源之水．其次，是想象性推理的發生．就是學生探索知識向更高水平的抽象層面發展，進行思維的攀爬，在一定的條件下想象，進行再推理，從學生的認知發展角度來講，就是他們認知結構中圖式的再豐富、認知過程的再深入環節．再次，是學生在推理過程中對自己獲得的知識經驗的創新運用，并經過抽象（推廣）對新的數學理論知識獲得發展．

練習是小學數學教學的一個重要組成部分，但是在實踐中，由于大部分教師對于數學知識的新授環節都能做到多角度深層次思考、多維度精細化設計，但是對于練習設計一般都是以“量”為主，而忽視了對練習“質”的思考，導致大量機械、重復、低效的練習．

延展性練習一般是在教學新知后，教師根據學生知識架構情況，有針對性地設計的包含豐富內涵的練習．在操作階段中，聚焦于學生在推理中發展新數學知識的抽象能力、內涵品質提升的延展性練習教學，其特點主要有以下3個．一是有基礎點，那就是這種練習教學要適應學生已有的認識經驗，能讓學生針對問題通過已有知識方法進行演繹性運用，并使問題得到解決，以獲得首次成功的喜悅．二是有觸發點，以首次成果為核心進行拓展，能為學生提供一定的事實條件和情境，以此作為學生營造合情推理的心理場域，并凝結成思維啟迪的動力，觸發他們去合情推理．三是有延展點，教師設計引導學生逐步從條件合情推理結果的指向問題，并富有一定的彈性力度和最近發展區水平．把問題吊在半空中，引著學生一步步向思維更深處漫朔．讓學生通過跳一跳摘到果子，獲得新的數學理論知識發展，即獲得再認識、再提升的發展．這里所說的延展性練習是通過兩種推理互補應用的延展性練習教學．

3 教例及剖析

3.1 操作數軸的延展性練習 在兩種推理互補應用中獲得對小數概念的新認識

小學五年級“認識小數”一課，新授環節中，在學生經過現象、心象，抽象概括出小數意義后，操作階段如何促使他們推理、發展新知識．

在小學數學教學中數軸是認識數的重要工具，它的出現，不僅可以讓學生對小數意義的認識更加深刻，而且可以使學生逐步感悟小數的特征，從而發展小數知識的內涵與外延．這里教師可以先設計讓學生運用已有的小數概念，在數軸上細分，對具體的小數形成深刻理解，再通過3個遞進層次的推理想象，讓學生感受小數的無窮性，以及去觸摸最小或最大的小數無限漸變并接近某一個極限的知識．具體如下所示．

首先選擇一個特定區間，也是最簡單的區間[0, 1]．有了學生對小數知識的基礎認識，要求學生運用小數概念在數軸上通過把0和1之間的一段平均分成10份，找到0.1的位置；再通過把0和0.1之間的一段平均分成10份，找到0.001的位置；繼續通過把0和0.001之間的一段平均分成10份，找到0.000?1的位置；通過直觀位置的對比，讓學生清晰地看到，這幾個小數中最接近0的小數是0.000?1，并且在0與0.000?1之間，通過把這一段再平均分成10份，還可以找出比0.000?1更小的小數0.000?01；在0和0.000?01之間，還可以推想出比0.000?01更小的小數……，最小的小數會漸近于0．

爾后是通過類比聯想，學生很容易就可以推想出既然在0與1之間，可以找到無數個小數．同樣，1和2之間、2和3之間也有無窮多個小數，最小的小數會漸近于1或2．這樣，通過觀察、想象和推理，學生可以知道在每兩個整數之間都存在著無窮個小數．并且得出“這些小數是漸漸變小，其中最小的一個會接近于某一個整數”的新發現．

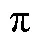
進一步再往深層次發展．數軸不斷向右延伸，學生在數軸上依次找到15.8，25.7，100.9，358.9，8?844.47……在數軸向右無限延伸的動態過程中，學生不僅看到了小數變得非常非常大，從而明白小數其實并不小，再加上學生的合理推想，就可以感受到小數也具有無窮大的特征，這一新的知識就是學生對小數概念的發展．

通過這樣逐步深入的延展性練習教學，讓學生在運用小數概念去理解某些具體的小數意義的基礎上，再為他們提供一連串的材料和情境，引導他們合情推理，感受無限，觸摸極限，并明白數軸上緊密排列著的每一個點都可以用不同形式的數來表示，這樣就在學生心中有效地發展了小數的內涵與外延，為他們的后續學習奠定基礎．

這就是“三象一作”中所說的，在對知識不斷運用和不斷認知中再提升的階段．也是一個應用了觀察、聯想、類比、猜測等合情推理的方法與合乎邏輯法則的條件上操作運用抽象的數學知識與數學方法（包括數軸這樣的數學符號及語言）去處理數學問題，并進一步發展數學理論知識的過程．

3.2 操作跳格游戲的延展性練習 在兩種推理互補應用中加深對列舉法的認識

數學教學既要生活化，又要不失“數學味”．在構造練習的延展性教學中，情景設計非常重要[8]．寓知識發展于情境之中，讓學生在情境中感悟數學萌芽、生長和變化的演繹過程，有效構建知識體系，提升數學能力．如教學“列舉策略”（蘇教版小學數學五年級上冊第96頁例2）．學生通過解決球賽中的場次等實際問題，建立了列舉策略的模型，為了讓學生對列舉策略有更進一步認識，教師可以設計這樣的延展性練習：小白兔玩跳格游戲，首先從外面跳到第1格，然后每次可以向前跳1格或2格，那么從格子外跳到第3格有幾種方法（如圖1）？格子數如果增加到4格呢？進而思考：如果格子數繼續增加到10、20甚至100呢？

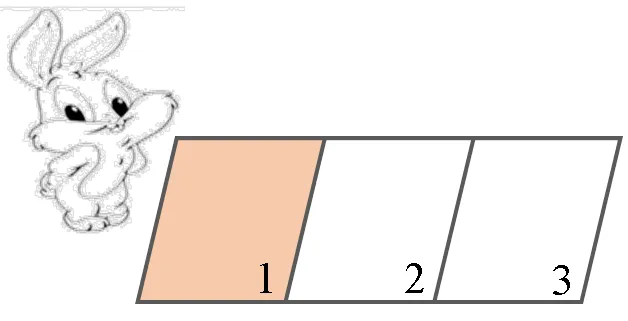
圖1 小白兔跳格游戲示意

展開時，可以運用多媒體模擬演示小白兔玩跳格游戲，讓學生厘清游戲規則，建立條件要素具象．進而引導學生運用已有的列舉方法，獲得從外面跳到1、2、3及4格的跳法種數．這樣的設計一改過去孩子們學習的被動局面，使他們對探索規律產生濃厚興趣，整個教學過程進入直覺與邏輯交融的主旋律中．下面只給出主要結果，具體教學過程略．

從外面跳到1和2，只有1種方法；跳到3可以一格一格跳，還可以從1直接跳到3，因此有2種；進而跳到4，有3種（動畫演示，如圖2）．上述列舉的結果，是學生在合情推理的基礎上運用演繹推理的成果．把這種連線法繼續有序地往下邊想邊推，還可以找到格子數是5、6、7……的所有跳法呢．（如圖3）

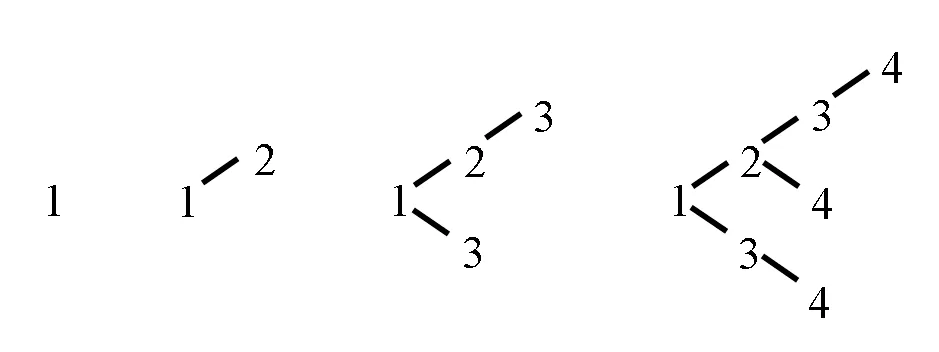
圖2 跳法種數示意

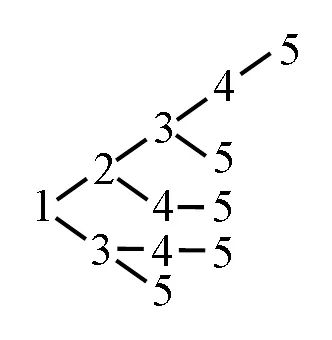
圖3 格子數是5的跳法

如果格子數繼續增加到10、20甚至100的時候，仍然用這種連線法，就會感到非常麻煩了．那么，這里面有沒有隱藏著什么規律，可以找到更簡便的方法來解決這個問題呢？這就要靠人們的智慧了．

歸納一下：跳到第一格有1種方法，跳到第二格也有1種，跳到第3格有2種，跳到第4格有3種，跳到第5格有5種……，列表標明方法的數量（見表1）．

表1 格子數與方法數

回憶一下（注：回憶舊知識也是一種延展）：從表中的方法數來看，很像以前學過的數列：1、1、2、3、5、……．

終于發現、找到規律：從第三項起，每一項等于前兩項的和．

那么，到底有沒有一個公式來計算呢？這個問題延展到課后去探索與思考．通過這套延展性練習，加深了學生對列舉法的認識．

3.3 確定基本形的延展性練習 在兩種推理互補應用中 實現了5種直線圖形面積公式的綜合建構

小學五年級學生已經經歷了長方形、正方形、平行四邊形、三角形、梯形等面積計算方法的推導及應用．在單元知識整理課上，教師設計了以“基本形”（當然它的選擇是相對的）為基礎，溝通5種直線圖形面積公式內在聯系的延展性練習教學．

復習整理5種圖形面積公式推導過程，把分散在各節課中學習的相關直線平面圖形的面積知識，按照一定的邏輯關系進行溝通，形成整體，這里的單元格是基本形．（如圖4）

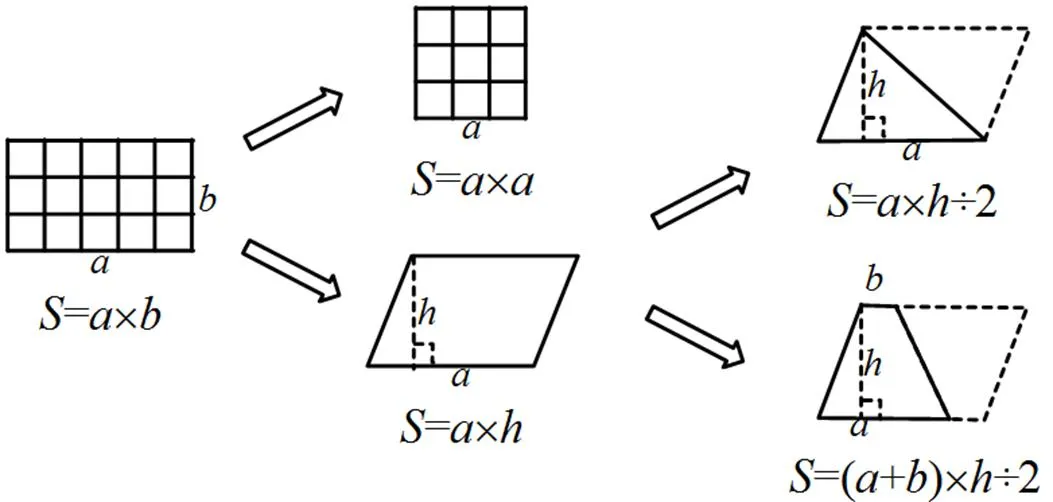
圖4 5種圖形面積公式

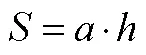
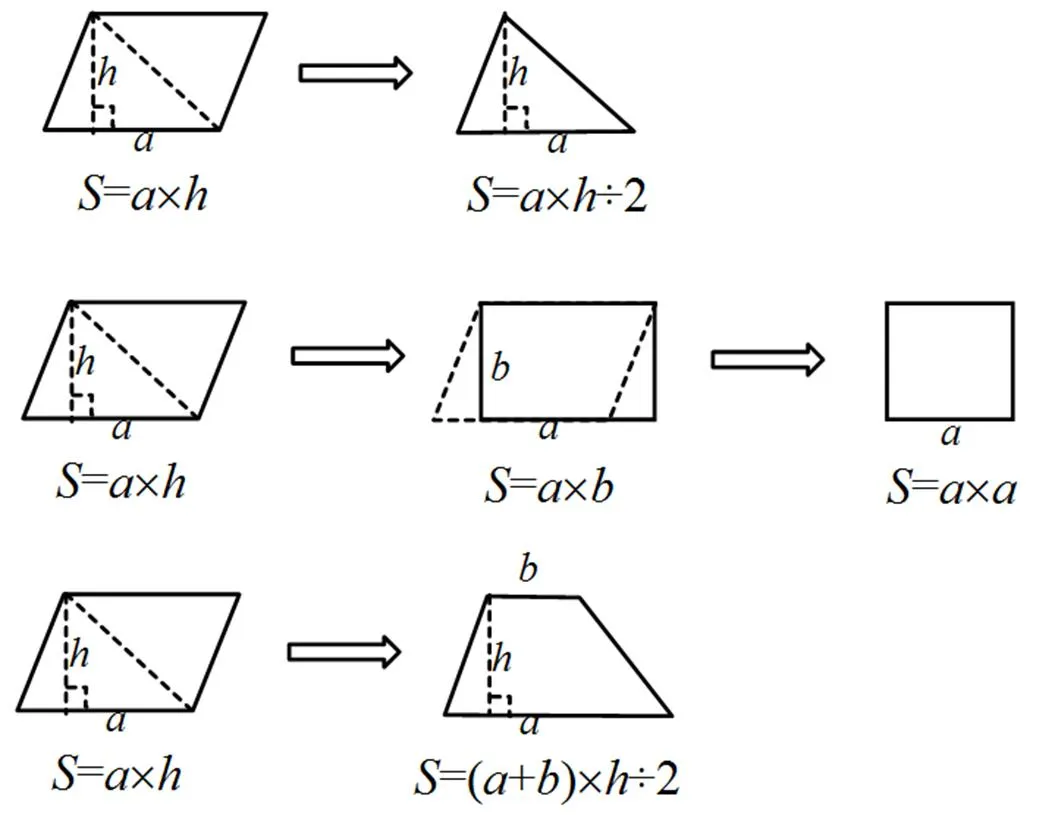
圖5 5種圖形面積體系

很顯然，這是學生在原有知識與方法的基礎上借助圖形變換進行合情推理，此刻已經獲得了溝通平面圖形面積之間聯系的一種新的結果．

教師再創設條件與情境，以梯形作為基本形，引導學生歸納分析直線平面圖形面積公式的共性．首先運用課件進行動態演示，將一個梯形的上底向一端逐漸縮短，一直縮到某個端點（如圖6），接著讓學生思考：上底可用什么表示？（0）此時，梯形變成了什么圖形？（三角形），然后教師用提問引發學生想象，直線平面圖形之間有著聯系，那么它們抽象的面積公式之間是否也存在聯系呢？引導學生用梯形的面積公式計算這個變化得來的三角形的面積：

這正好是三角形的面積公式．

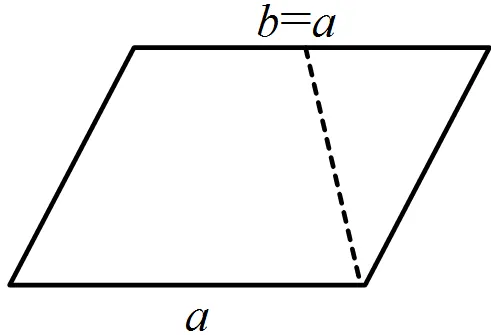
圖7 梯形變成平行四邊形

接著又演示梯形的上底（假設<）向一邊逐漸延伸，一直延伸到與下底同樣長（如圖7），這時候=，梯形就變成了平行四邊形．這時要求學生用梯形面積公式計算這個變化來的平行四邊形面積，從而得到平行四邊形面積公式：

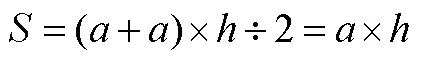
同樣地，再讓學生根據圖形動態變化，想象演變成長方形和正方形（如圖8、圖9），再用梯形面積公式推出長方形和正方形的面積計算公式：

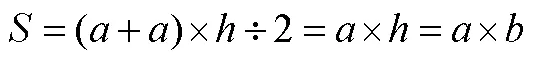
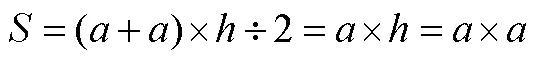
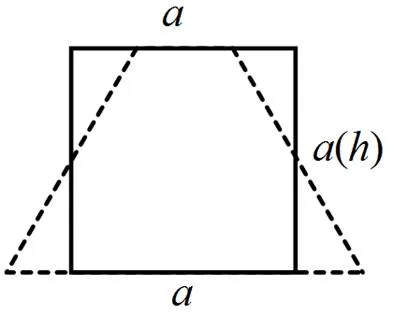
圖9 梯形就變成正方形

這樣的延展性練習教學，教師通過演示，引導學生想象，不僅發現5種直線平面圖形之間的聯系，而且抽象的直線平面圖形面積計算公式之間也有著聯系，這里可用梯形面積公式來統整，這樣的操作，把知識串線連片，結成了網絡，從而讓學生獲得直線平面圖形面積計算內在邏輯的全新知識．

【效果分析】通過諸如上述這些具有可操作性的延展性練習教學的設計與實踐，老師堅持把數學教學過程中的語言傳遞、直接感知、實際訓練、引導探究、活動欣賞等幾種常用方法融成了一體．學生在兩種推理交互作用中發展了數學新知識．為此，還專門請了有關研究人員對“中學生一般能力傾向測驗”中的“數學推理”這個項目作修改，把它改造成適合于小學生的測量工具，運用它對實施一年后的實驗班學生進行測試．在方差齊性的前提下，對平均數差數進行顯著性檢驗的結果表明：小學生在數學推理這個項目上，均極其顯著或顯著優于實驗初的水平（已考慮相關系數和系統誤差），如表2所示．學生在空間想象能力和計算能力方面的測量有待于進一步研究，不同年齡段的學生需要使用不同的測試工具和方法，因此打算先進行“設計研究”[10]．另外非智力因素對人的發展格外重要，更應該重視學生非智力因素方面的培養與提高．延展性練習教學也有助于學生非智力因素方面的建設．學生的意志、信念、合作精神等非智力因素都有所改變；反之，非智力因素的培養與提高對學生數學學習成績的提高也有著積極的促進作用．它們都是相輔相成的．只要編制適當的量表，還可以探究它們的相關度，即相關系數，求出非智力因素與智力因素這兩個變量之間的回歸方程，有興趣的讀者盡可參見“大中小學班集體建設的人機模型和統計分析”[11-12]．

4 延展性練習教學中兩種推理交互作用的進一步詮釋和關于數學教學終極目標的一點思考

延展性練習教學的目的是要高標準地提高學生的數學核心素養．當然其過程是逐步實現的，不能一蹴而就．需要反復進行訓練，延展與鍛造．俗話說數學是思維的體操，數學教育的目的是要培養學生學會“數學地進行思維”即數學推理，用數學的思想方法去考慮和處理問題．數學推理主要有兩種，所謂的合情推理與演繹推理，前者也叫似真推理，后者可叫邏輯推理．

數學內部的發展依賴的就是邏輯推理．愛因斯坦認為：“適用于科學幼年時代以歸納為主的方法，正讓位于探索性的演繹法．”[9]探索性的演繹法應該全面地理解為歸納基礎上的演繹，數學的理解鏈是：“直覺—嘗試—出錯—推測—猜想—證明．”其中的推測和猜想是合情推理的過程．而證明則是對推理的檢驗和論證．如果發現矛盾，則要重新提出猜想．可見，合情推理與演繹推理是數學鏈條中不可缺少的環節．演繹推理的特征是邏輯嚴謹，合情推理的特征是想象豐富，相互之間并不矛盾．相反，它們互相補充．直覺具有洞察力．萊布尼茨說過，人們依靠直覺洞察力，“往往一眼就能看出我們靠推論的力量在花費了許多時間精力以后才能找出的東西”．然而，這種直覺洞察力要以邏輯分析為“前奏”，又要以邏輯推理來“補臺”．過分強調直覺在科學發現中的作用，而低估邏輯發現的力量是一種短視的見解．直覺問題很復雜，直覺中有理性因素，也有非理性因素；有邏輯因素，也有非邏輯因素；要看到它們的辯證統一．將直覺看成是一個純粹的邏輯問題，顯然是不妥的；但是，將直覺看成是一個純粹非邏輯的心理因素，那也是不妥的．

徐利治先生把直覺與邏輯比喻為“眼睛和雙腿”，他說：“從事數學創造性研究如同人在迷霧中摸索前進那樣，需要用眼睛辨別方向，用雙腿邁向目的地．直覺好比眼睛，起向導引領作用．邏輯就是雙腿，沒有邏輯不可能達到目的地．”總之，直覺思維運籌帷幄，邏輯思維循規蹈矩，在數學的思維過程中兩者交相輝映[13]．因此，教學過程中應該既要重視合情推理，又要重視演繹推理．兩者不可偏廢．要引導學生經歷完整的推理過程，即發展學生合情推理能力與邏輯推理能力交融的數學綜合思維能力．

數學思維到了一定境界，思考和解決問題往往不是用公式和數字來運算，而是用思想來運算．這就是所謂的“用數學的思維想問題”．正是文獻[2]所指出的那樣，在赫爾巴特那里，教學總是使兩方面日臻完善——人的智力與道德．它是教學也應該是數學教學的終極目標．王梓坤院士在“今日數學及其應用”一文中指出：“數學中嚴謹的推理和一絲不茍的計算，使得每一數學結論不可動搖．這種思想方法不僅培養了數學家，也有助于提高全國人民的科學文化素質．它是人類巨大的精神財富．”[14]而教師通過數學教學培養學生用數學思維想問題的習慣，達到上述終極目標也就不遠了．在本質上，這樣的目標不是教師短時間內“教”出來的，而是學生悟出來的，是長期經驗的積累，是在一系列教學過程中慢慢形成的．《數學課程標準》把推理能力作為數學教學的重要內容之一，認為“推理能力的發展應貫穿在整個數學學習過程中”，并在“數學思考”的課程目標中明確要求：在參與觀察、實驗、猜想、證明、綜合實踐等數學活動中，發展合情推理和演繹推理能力，清晰地表達自己的想法．明確指出發展合情推理和演繹推理在數學教學中是密切聯系、相輔相成的．所以在教學中要根據不同階段和不同知識內容，去探索如何優化組合，互補應用，發揮其在認知發展中的最大效益．教師在設想過程性目標時，不僅要說“經歷什么”“探究什么”，還應該明確“得到什么”．教師備課不應局限于某一堂課，而應該把相對成邏輯體系的知識整合在一起，思考通過這些課程怎樣將學生自如地應用兩種推理思考數學問題的能力培養，落實到常態的教學中．只有這樣，讓學生養成用數學思維去想問題的習慣，才算是把開啟數學知識大門的鑰匙交給了學生．如果沒有達成這一目標，那么不算是獲得成功的教學．

【研究結論與討論】人們把物質的延展性這一物理屬性擬人化（指人的可塑性），老師抓住幾個典型案例，首先從學生感悟小數的特征建立數感[15]開始；接著操作跳格游戲，讓學生在情境中感悟數學的演繹過程，構建知識體系提升數學能力；最后教師引導學生共同演示直線平面圖形面積計算公式之間的聯系，把知識串線連片結成了網絡，實現了5種直線圖形面積公式的綜合建構，從而讓學生獲得了面積計算內在邏輯的全新知識．實踐證明數學課堂的延展性教學這種教學方法在小學數學教學中是可行的、有效的．通過延展性數學教學，對數學教學過程進行延伸與拓展，推廣、擴充和遷移數學知識，有利于培養和發展學生的創造性思維能力，獲得廣闊的思維空間，找到新的方法與觀點，更好地解決數學問題，發展數學新知識．尤其是把延展性教學與“三象一作”的數學認知過程結合起來，重在可操作性，把數學教學變得有血有肉，把抽象的數學知識形象化、具體化，數學已不再是一些數字和符號的堆砌，調動了學生的學習興趣和學習主動性，在“直覺—嘗試—出錯—推測—猜想—證明”等一些數學的理解鏈上，為學生在今后能自如地應用合情推理和演繹推理這兩種思維模式打好基礎．

討論：實際上，延展性數學教學與優智教育方案在下列幾個方面是接軌的．它意味著課堂教學內容在深度和廣度上的拓展，它實質上要提供給學生一個比正常課程內容層次更高的課程知識，它將給予學生更復雜的信息，涵蓋更密集的材料，對學生具有更大的挑戰性．它強調知識之間的聯系，上位知識和下位知識、新舊知識、課堂知識與生活實踐知識之間的聯系，重視對呈現效果的檢測與反饋．這樣的教學設計，通過典型事例激發學生的機智，促進學生認知過程的優化，提升認知水平與層次，為提高學生高層次數學認知能力打好小學基礎．

從上看到，研究與實踐在具操作過程中盡管也重視了數學知識的層次性和學生認識過程的層次性，也是由淺入深，由易到難，由簡單到復雜，尤其是與數學的認知過程，與元認知理論，與情感度相融通．但在某種意義上說，它還應該考慮到不同學生的認知基礎、認識方式的差異，必須為學生呈現多樣化策略的應用與選擇．因此有專家建議，如果“在延展性數學練習的界定或理論化過程中，能夠增強與相關理論體系（例如數學習題的層次水平）的關聯和比較”，那么就能使這種研究與實踐“更具開放性和推廣性”．因此，研究者今后將在延展性練習教學的數學習題設計上進一步下功夫．還可以把它與數學問題和習題教學中的變式訓練等結合起來．一線數學教師為此創造了許多有效的理論與方法．例如，從模仿型基礎訓練，到拓展型變式訓練，再到遷移型創新訓練，等等[16]．總之，既關注教材，更關注學生，也就是傳統教學中所說的“備兩頭”．數學課堂教學的關鍵是教學設計，只要首先抓緊和進一步完善這個重要環節，那么延展性練習教學必將別開生面．

致謝：無錫市大橋實驗中學楊錫偉先生審閱了文稿并給出了有關圖表，誠致謝意！

[1] WANG G. Characteristics of efficiency of mathematical instructional behavior [J]. Journal of Mathematics Education, 2013, 6 (1): 59–62.

[2] 劉萬海．真正教學的意味——基于赫爾巴特“教育性教學”思想的延展性思考[J]．全球教育展望，2011，40（9）：9–12，18．

[3] 孫華．有效延展，促進內化——高中數學延展性教學的幾點思考[J]．數學教學通訊，2017（7）：56–57．

[4] 王愛軍．對小學數學課堂中延展性問題的思考[J]．小學教學研究，2009（4）：26–27．

[5] 逯美玲．做數學課上的“有心人”——淺談數學課的延展性[J]．小學教學研究，2018（12）：76–78．

[6] 許光新．兒童數學思維的復雜性及對小學數學教學的啟示[J]．教師教育論壇，2016，29（4）：32–35，47．

[7] 王名揚，徐瀝泉，徐利治．論一種緣自認知心理學及教育學研究的數學認知過程[J]．數學教育學報，2013，22（1）：33–36．

[8] 章漢平．延展性數學情境設計與思考[J]．好家長·新教育，2007（8）：34–35．

[9] 沈三思．愛因斯坦的科研方法[J]．青年科學，2004（7）：4–5．

[10] 李卓，鮑建生．論設計研究：“內涵”“類型”“過程”與“應用”[J]．數學教育學報，2020，29（5）：2–57．

[11] 王光明，彭宇佳，李建．小學高年級學生數學學習非智力因素常模及其等級評價標準的建構與應用[J]．數學教育學報，2021，30（3）：52–58．

[12] 徐瀝泉．大中小學班集體建設的人機模型和統計分析[J]．統計學與應用，2013（2）：37–50．

[13] 徐瀝泉，孟勇．數學的旋律——直覺與邏輯交融[J]．自然雜志，2009，34（5）：239–244．

[14] 王梓坤．今日數學及其應用[J]．自然辯證法研究，1994，10（1）：3–17．

[15] 孫虎，張偉平，陳志輝，等．基于核心素養的六年級學生數感現狀調查研究[J]．數學教育學報，2021，30（4）：41–47．

[16] 袁保金．數學習題訓練的三個層級及其教學思考[J]．河北理科教學研究，2015（4）：31–33．

To Manipulate the Exercise Teaching of Ductility and Malleability: Developing New Mathematical Knowledge in the Interaction of Two Kinds of Reasoning

GU Li-ying1, DENG De-wei2

(1. Wuxi Xinzhou Primary School, Jiangsu Wuxi 214112, China;2. Hongze Experimental Primary School of Huai’an City, Jiangsu Huai’an 223100, China)

Under the condition that the macro background and educational environment remain relatively unchanged, improving teaching methods is the fundamental measure to improve teaching quality.Various teaching methods emerge in an endless stream, and their types and definitions are more specific, more precise, and more professional. Ductility teaching is one of them.Ductility is a physical property derived from matter, which refers to the degree to which it can be tempered and calendared. Here, it is used in mathematics teaching to temper a person’s mathematical quality and ability, so as to improve students’ mathematics competencies to a high standard. After reviewing and analyzing the characteristics and models of this teaching method, it was incorporated into the “three images and one work” mathematical cognitive process of cognitive psychology and pedagogy research. This ductility and malleability teaching practice was carried out by Wuxi Xinzhou Primary School and other schools. Teachers carefully design the teaching process, through some typical teaching examples, integrate several common methods such as “language transmission, direct perception, practical training, guided inquiry, and activity appreciation”, extend the interaction between plausible reasoning and deductive reasoning, expand mathematical thinking activities, and develop mathematical knowledge. Through statistical analysis, students’ mathematical reasoning ability has been significantly improved. Practice has confirmed that the teaching method of extension teaching in mathematics classroom is feasible and effective in primary school mathematics teaching.The direction of its efforts is: in view of the differences in the cognitive basis and cognitive methods of different students, the teaching design must also provide and present the application and selection of diverse strategies for students. In the process of further interpretation of ductility teaching, some thoughts are also made on the ultimate goal of mathematics teaching.

the process cognitive psychology (“three images and one work”); teaching of ductility and malleability; the plausible reasoning ability; logical reasoning ability; ultimate goal

2022–01–20

江蘇省教育科學“十一五”規劃重點項目——發生認識論與數學的抽象度分析法（C-c/2001/02/007）；江蘇省教學研究“十三五”立項課題——基于ELLI框架的多元文化背景下兒童學習力培養研究（2019JK13-L038）

顧麗英（1974—），女，江蘇無錫人，高級教師，主要從事小學數學教學研究．

G447

A

1004–9894（2022）03–0050–06

顧麗英，鄧德巍．操作延展性練習教學——在兩種推理交互作用中發展數學新知識[J]．數學教育學報，2022，31（3）：50-55．

[責任編校：周學智、張楠]