基于數學核心素養的新舊高考比較分析——以2021年新高考Ⅰ卷與2020年全國Ⅰ卷為例

李子瞻，胡典順

基于數學核心素養的新舊高考比較分析——以2021年新高考Ⅰ卷與2020年全國Ⅰ卷為例

李子瞻，胡典順

（華中師范大學 數學與統計學學院，湖北 武漢 430079）

新時期高考更加注重對學生數學核心素養的測量與評價．基于課程標準對數學核心素養水平的劃分及喻平對知識理解、知識遷移、知識創新三水平的描述，建立數學核心素養評價指標框架，并以此為依據對2021年新高考Ⅰ卷與2020年全國Ⅰ卷中考查的數學核心素養進行賦值．對賦值結果進行定量分析可知，新舊高考在數學運算、邏輯推理、直觀想象3類素養上的考查權重較高；新舊高考在單個素養的考查水平上各有側重，同水平在總體分布上沒有顯著差異，且偏向于對知識理解與知識遷移水平的考查；新高考不分文理，難度調控更為科學．基于分析結果得到如下啟示：高考命題應當堅持素養導向，穩步優化改革；教學應當適應考核形式，滲透數學思想．

數學核心素養；高考改革；新高考卷

1 問題提出

自1977年恢復高考制度以來，中國已初步形成相對完整的考試招生體系，并不斷圍繞“促進教育公平、提高選拔水平”進行完善[1]．國務院2014年頒布的《關于深化考試招生制度改革的實施意見》中提出，為更好地貫徹黨的教育方針，全面實施素質教育，有序推進高考改革，選擇有條件的地區啟動高考綜合改革試點[2]．至2021年，共有14個省市參與新高考．新高考試點使得不同地區的教育改革程度有所不同，2021年高考，教育部考試中心為對不同改革程度及不同教育水平的地區進行相對公平的考試招生，命制了包括全國甲卷（理科）、全國甲卷（文科）、全國乙卷（理科）、全國乙卷（文科）、新高考Ⅰ卷（不分文理）、新高考Ⅱ卷（不分文理）在內的6套考卷，其中新高考卷針對的是參與統考的試點地區．14個參與新高考的省市中，河北、湖北、湖南、福建、廣東5省是由2020年的全國Ⅰ卷過渡到了2021年的新高考Ⅰ卷．

2014年《教育部關于全面深化課程改革落實立德樹人根本任務的意見》中提出研究制定學生發展核心素養體系，并將核心素養落實到各學科中，提升學科的育人價值[3]．新時期高考改革的新目的、新要求就是突出對數學核心素養的考查，將目光放在學生未來的發展上，更好地發揮高考立德樹人、服務選才、引領教學的作用[4]．這里以2021年新高考Ⅰ卷數學和2020年全國Ⅰ卷數學（選做題不予考慮）為例，比較分析新舊高考對學生數學核心素養的考查情況．

2 研究方法

2.1 數學核心素養評價指標框架的建立

《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“2017年版課標”）指出，數學學科核心素養是具有數學基本特征的思維品質、關鍵能力、情感、態度與價值觀的綜合，是數學科育人價值的集中體現[5]．2017年版課標中提出，數學核心素養包括數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析六大成分[5]．數學抽象素養要求能夠把握事物的本質，歸納概括出一般的概念或命題，體現了學生的理性思維與抽象概括能力；邏輯推理素養是指從已知條件出發，依據一定的規則，驗證或得出結論的能力，彰顯了學生思維的嚴謹性、邏輯性；數學建模素養要求能夠對現實問題進行抽象，用數學語言表達問題，并用數學方法解決實際問題，體現了學生的模型思想和創新意識；直觀想象素養指的是能夠借助幾何直觀建立數與形的關系，體現了學生的空間想象能力與數形結合的思想；數學運算素養指的是能夠合理地使用運算法則進行正確的運算，它是解決數學問題的基本手段；數據分析素養主要指學生借助概率與統計的相關知識分析處理數據，獲得和解釋結論的能力[5]．這六大數學核心素養既相互獨立，又相互滲透，是一個有機的整體，以數學知識為本源，在學生學習的過程中逐步形成，為學生未來的發展奠定基礎[6–8]．

2017年版課標中還給出了核心素養的三水平劃分，喻平認為課標中的劃分缺少一定的依據與指導意義，他指出，核心素養的培養要以知識為載體，并進一步從知識學習方面入手將核心素養水平劃分為：知識理解、知識遷移、知識創新[9]．知識理解即理解知識的本質類屬及知識間的關系，并具備基本的運算、推理技能；知識遷移是指能夠將已有的知識或技能遷移到不同的情境中，解決不同條件下的問題，促進新知識的習得；知識創新是知識學習的最高水平，它是指學生已經形成了一定的數學思維和數學觀，能夠超越既定的知識，提出有建設性的看法，具備一定的探究意識、直覺能力、反思能力和批判性思維[10]．根據喻平對知識理解、知識遷移、知識創新的描述[10]，結合2017年版課標中數學學科核心素養三水平的劃分[5]，建立如表1所示評價指標框架．

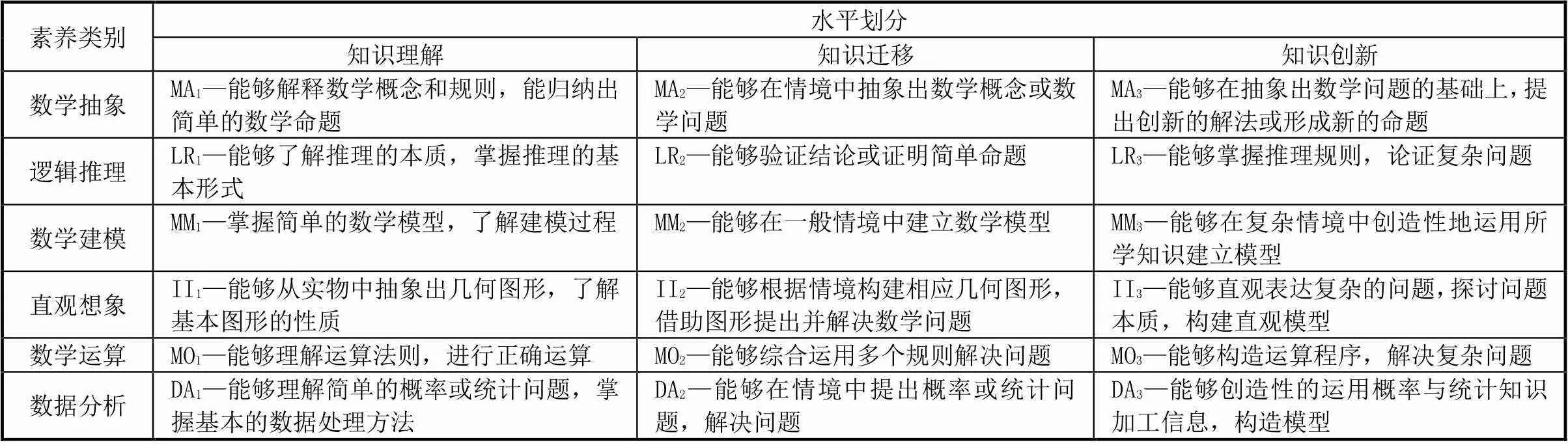
表1 數學核心素養評價指標框架

注：數學核心素養水平的命名采用六大核心素養的英文首字母，下標1、2、3分別對應3個水平，如MA1代表數學抽象的知識理解水平．

2.2 數學核心素養評價指標量化賦值

由于六大數學核心素養并非完全獨立存在，它們是互相補充、互相關聯的，具有一定的交叉性，因此一道題目中往往能夠考查學生的多種素養，但在不同的知識模塊中側重體現的素養類型又有所不同[11]．

為明確各題的考查情況，有必要對題目所含數學核心素養進行量化賦值．李華、胡典順基于喻平對數學核心素養水平的劃分，細化核心素養評價標準，對2019年高考全國卷賦值并分析[12]．張玉環等采用李華的評價標準對2015—2020年中法高考試卷進行比較研究[13]．這里的賦值模式同樣參考李華等人的研究，并在以往研究的基礎上進一步對評價標準進行了探索．依據表1中的評價指標框架，對2021年新高考Ⅰ卷與2020年全國Ⅰ卷試題中所含數學核心素養類別及水平進行劃分，并在此基礎上，結合參考答案與題目分值對試題所含各數學核心素養進行量化賦值．下面以2021年新高考Ⅰ卷第17題為例進行賦值說明．

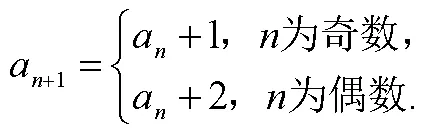
參考答案

3 研究結果

3.1 數學核心素養整體考查情況分析

由于題目量較大，不便一一列出賦值過程，為使評價更加準確，現對賦值結果進行整理，并將每套試卷中各水平各類型的數學核心素養分值轉化為占整份試卷總分的權重．以數學抽象素養為例，MA1的權重計算方式為整份試卷中數學抽象素養在知識理解水平上的考查分值除以試卷總分，其中2021年新高考卷總分為150分，不包含選做題的2020年全國卷總分為140分（以下將2020年全國Ⅰ卷理科簡稱為理科卷，2020年全國Ⅰ卷文科簡稱為文科卷，2021年新高考Ⅰ卷簡稱為新高考卷）．現將六大數學核心素養考查頻數及權重匯總如表2所示．

表2中列出了數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析六大數學核心素養在知識理解、知識遷移、知識創新3個水平上的考查情況．可以看出，3份試卷對于數學核心素養的考查都比較全面，六大核心素養都有所涉及．

根據表2整理出六大數學核心素養的考查水平分布，如圖1所示，權重最高的3項為數學運算素養、邏輯推理素養、直觀想象素養，這與張奠宙認為的數學素質應當包含數學運算能力、邏輯思維能力、空間想象能力三大能力相契合[14]．

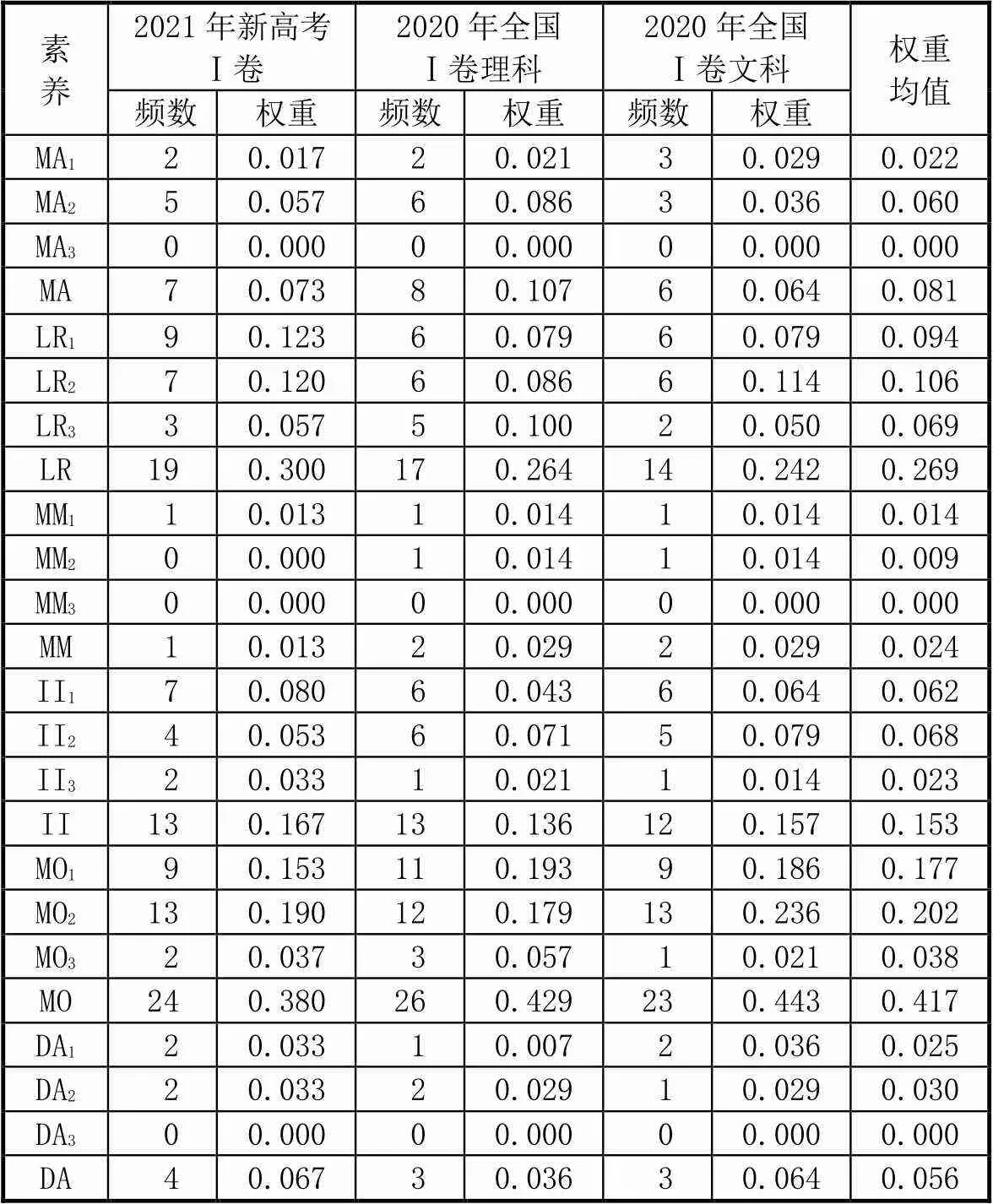
表2 新舊高考數學核心素養權重值匯總

注：結果均保留三位小數

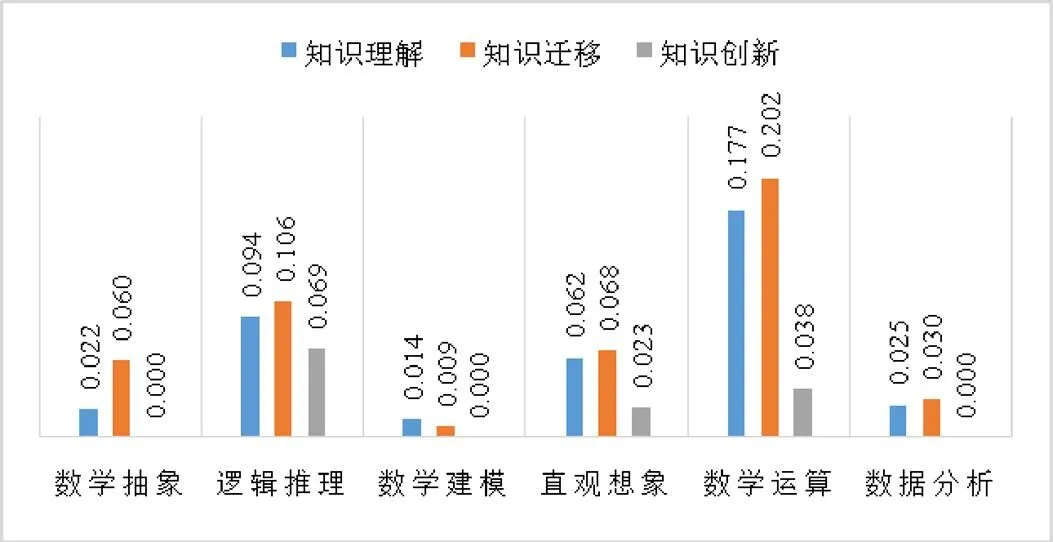
圖1 六大核心素養三水平考查權重分布

數學抽象素養和數學建模素養盡管所占權重值略低，但這兩者更加突出對學生理性思維的考查，理性思維在數學核心素養中起到非常重要的作用，對學生的要求也比較高．數據分析素養考查的大多是關于學生概率與統計方面的知識，每年考查的比重都較為穩定，但權重值也較低．各類核心素養在考查水平上總體傾向于對知識理解與知識遷移水平上的考查，對知識創新水平的考查較少．

3.2 數學核心素養考查水平對比分析

對于由2020年全國Ⅰ卷過渡到2021年新高考Ⅰ卷的5個省份來說，數學科最大的改變就是不再區分文理科，因此新高考卷的題目命制既要兼顧學生的不同水平，又要能夠較為全面地考查學生的各項能力，突出基礎性、綜合性、應用性、創新性的考查要求[15]．因此考卷中對核心素養水平的把控尤為重要，下面對新舊高考數學核心素養考查水平做進一步分析．

3.2.1 知識理解水平

知識理解屬于知識學習的一級水平，它指的是學生對數學概念和規則的認識以及對數學方法和技巧的理解[10]．圖2顯示了3份試卷中知識理解水平上的數學核心素養考查情況．該水平數學抽象素養的考查中，文科卷考查的權重較高，權重值為2.9%，理科卷考查的權重值為2.1%，新高考卷考查的權重值為1.7%，數學抽象素養需要學生有嚴謹的數學思維，但在該水平上對考生的要求不高，主要要求學生能夠解釋數學概念和規則，歸納出簡單的數學命題即可[5]．邏輯推理素養的考查中，新高考卷考查權重明顯高于理科卷和文科卷，權重值為12.3%，理科卷和文科卷考查的權重值持平，均為7.9%．邏輯推理素養在該水平上要求能夠了解推理的本質，掌握推理的基本形式[5]，體現了對學生理性思維的考查，新高考重視學生邏輯思維的同時又要兼顧其基礎性的考查要求，因此在知識理解水平上的考查權重較高．3份試卷對于學生數學建模素養的考查都比較少，該水平上文科卷和理科卷數學建模素養的考查權重均為1.4%，新高考卷為1.3%，數學建模是數學學科和學生實際生活之間的橋梁，知識理解水平要求學生能夠掌握簡單的數學模型，了解建模的過程．

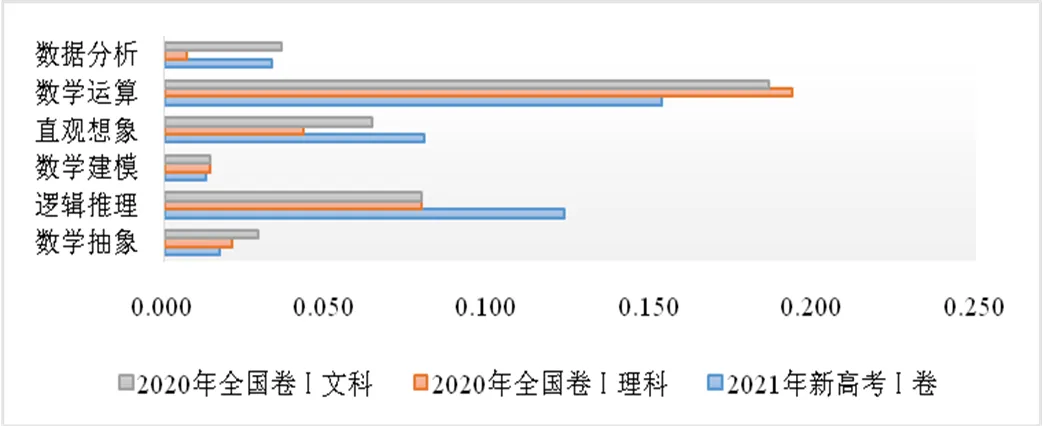
圖2 知識理解水平上六大核心素養的考查情況

該水平上直觀想象素養的考查中，新高考卷考查的權重較高，權重值為8%，文科卷考查權重為6.4%，理科卷考查權重為4.3%．直觀想象素養與學生的空間想象能力有著密不可分的關系，知識理解水平上要求能夠了解圖形的基本性質，從實物中抽象出幾何圖形，借助圖形認識數學問題[5]．數學運算存在于大多數的解題過程中，因此3份試卷對于數學運算素養的考查都比較多，理科卷考查的權重為19.3%，文科卷考查的權重為18.6%，新高考卷考查的權重為15.3%．數學運算素養的知識理解水平要求能夠了解運算法則，形成運算思路并進行正確運算[5]．該水平多體現在較為基礎的題目中，如新高考卷單選題第1題、第2題．數據分析素養每年考查的權重都較為穩定，該水平上文科卷考查權重為3.6%，新高考卷考查權重為3.3%，理科卷考查權重為0.7%，知識理解水平要求能夠了解簡單的概率或統計問題，掌握基本的數據處理方法，對學生的邏輯思維要求不高，因此文科卷的考查權重略高，新高考卷的考查權重介于理科卷與文科卷之間．

3.2.2 知識遷移水平

知識遷移在知識學習中屬于二級水平，該水平要求學生能夠將已有的知識或技能遷移到不同的情境中，解決不同條件下的問題，促進新知識的習得[10]．圖3顯示了3份試卷中知識遷移水平上數學核心素養的考查情況．該水平上數學抽象素養的考查中，理科卷考查的權重最高，權重值為8.6%，文科卷考查的權重為3.6%，新高考卷考查的權重介于兩者之間，權重值為5.7%．知識遷移水平上的數學抽象素養要求能夠在情境中抽象出一般概念或規則[5]，學生需要熟練掌握所學概念并具有一定的抽象能力，如文科卷的填空題第15題．對該水平上邏輯推理素養的考查中，新高考卷考查的權重最高，權重值為12%，文科卷考查的權重為11.4%，理科卷考查的權重為8.6%．要達到該水平，學生需要能夠靈活運用所學概念，證明簡單命題，并用數學語言表達推理過程．知識遷移水平上數學建模素養的考查中，理科卷和文科卷的考查權重均為1.4%，而新高考卷則沒有涉及到該水平上的考查．數學建模往往與實際情境相結合，如在理科卷的選擇題第5題中，通過對某作物種子發芽率的散點圖進行擬合，判斷其函數模型，讓學生體驗從實際情境中發現問題構建模型的過程．

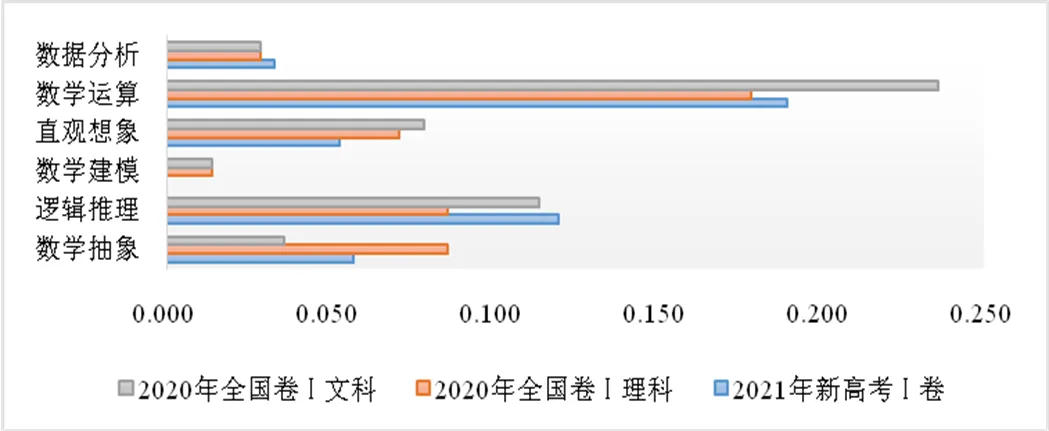
圖3 知識遷移水平上六大核心素養的考查情況

在知識遷移水平上直觀想象素養的考查中，文科卷考查的權重較高，權重值為7.9%，理科卷考查的權重為7.1%，新高考卷考查的權重為5.3%，知識遷移水平要求學生能夠借助圖形性質探索數學規律[5]，解決數學問題，充分考查了學生的數形結合思想，如新高考卷中多選題第11題．知識遷移水平上數學運算素養的考查仍然占據了較高的比重，文科卷考查的權重為23.6%，理科卷考查的權重為17.9%，新高考卷的權重值介于兩者之間，為19%．該水平上數學運算素養要求能夠選擇合理的運算方法[5]，綜合運用多個規則解決問題，在數學解題中的應用較為廣泛，如理科卷的第7題、第10題，文科卷第9題、第11題．知識遷移水平上數據分析素養的考查較為均衡，新高考卷考查的權重為3.3%，理科卷和文科卷均為2.9%．該水平要求能夠在情境中提出概率或統計問題，運用恰當的概率或統計模型解決問題[5]，如理科卷第19題、新高考卷第18題．

3.2.3 知識創新水平

知識創新是知識學習的最高水平，它是指能夠超越給定的知識，提出有建設性的看法，能夠形成自己的數學觀[10]．要達到該水平往往需要打破常規解法，另辟蹊徑，因此對學生的要求也比較高，但有一定難度的題目往往能夠顯著區分高層次考生，在選拔性考試中，此類題目的設置尤為重要[16]．圖4顯示了3份試卷中知識創新水平上的數學核心素養考查情況．在知識創新水平上數學抽象素養的考查中，要求學生能夠在抽象出數學問題的基礎上，提出創新的解法或形成新的命題[5]，該過程的難度較大，3份試卷均沒有涉及到這方面的考查．知識創新水平上邏輯推理素養的考查中，理科卷考查的權重最高，權重值為10%，文科卷考查權重為5%，新高考卷則介于兩者之間，權重值為5.7%．該水平主要考查學生掌握推理規則，論證復雜問題的能力，對學生的理性思維要求較高．知識創新水平上數學建模素養的考查要求能夠在復雜情境中創造性地運用所學知識建立模型[5]，學生不僅要能夠熟練掌握所學模型，還要能夠發現情境中的數學關系，創造性地建立模型，由于考試時間有限，學生在考場上完成這個過程的難度較大，3份試卷對此均未涉及．

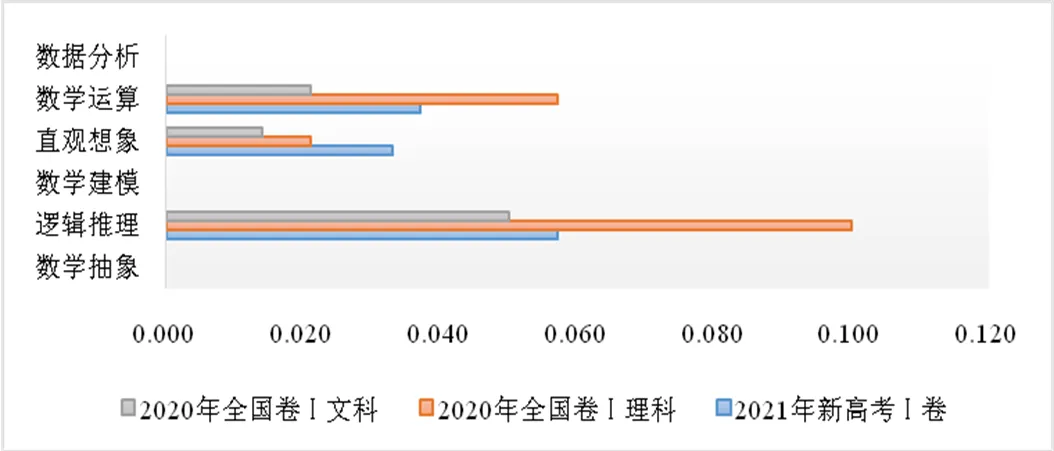
圖4 知識創新水平上六大核心素養的考查情況

在知識創新水平上直觀想象素養的考查中，新高考卷考查的權重為3.3%，理科卷考查權重為2.1%，文科卷考查權重為1.4%．容易看出，新高考卷考查的權重較高．該水平上的直觀想象素養要求學生能夠直觀表達復雜的問題，探討問題本質，構建直觀模型，如多選題第12題中選項C、D的考查．知識創新水平上數學運算素養的考查中，理科卷的考查權重較大，權重值為5.7%，文科卷考查權重值為2.1%，新高考卷介于兩者之間，考查權重為3.7%．運算能夠讓學生養成規范化的思考習慣和嚴謹的數學思維，該水平上要求能夠構造運算程序，解決復雜問題[5]．知識創新水平上的數據分析素養要求能夠創造性地運用概率與統計知識加工信息，發現統計規律，形成新的知識[5]．3份試卷對于數據分析素養的考查分布在知識理解與知識遷移水平，該水平上沒有涉及．

3.2.4 三水平總體分析

根據表2統計的權重值，將每套試卷中對6個素養在各水平上的考查權重匯總，如新高考Ⅰ卷中對知識理解水平的總權重為該試卷中MA1、LR1、MM1、II1、MO1、DA1的考查權重之和．得到如圖5所示的3份試卷在知識理解、知識遷移、知識創新3個水平上的考查權重．容易看出，這3份試卷在3個水平上的總體分布趨勢是一致的，均為知識遷移水平上的考查權重最高，知識理解次之，知識創新水平的考查權重最低．

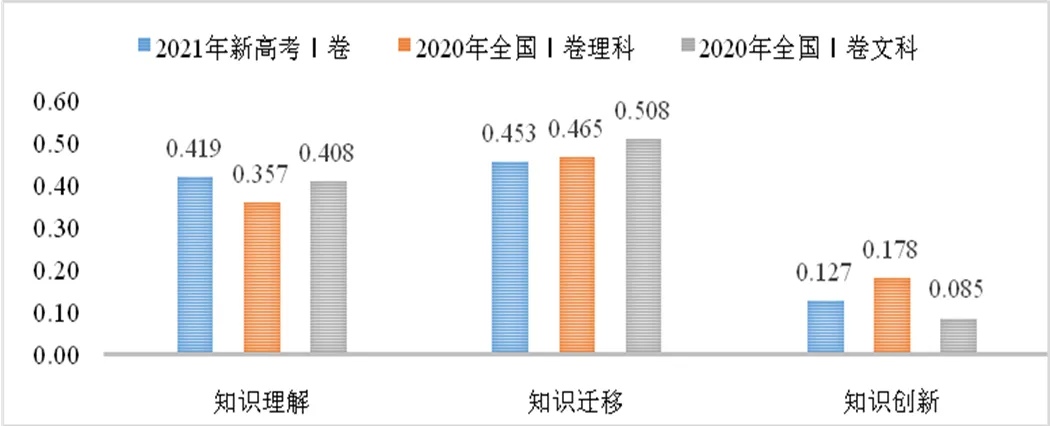
圖5 三水平權重分布

下面采用SPSS 27.0分析3份試卷中六大數學核心素養3個水平權重的總體分布是否存在顯著差異．根據數據特征，采用獨立樣本Kruskal-Wallis檢驗，在各個組之間自動比較分布．如表3所示，原假設為3個獨立樣本中三水平的分布無顯著差異．

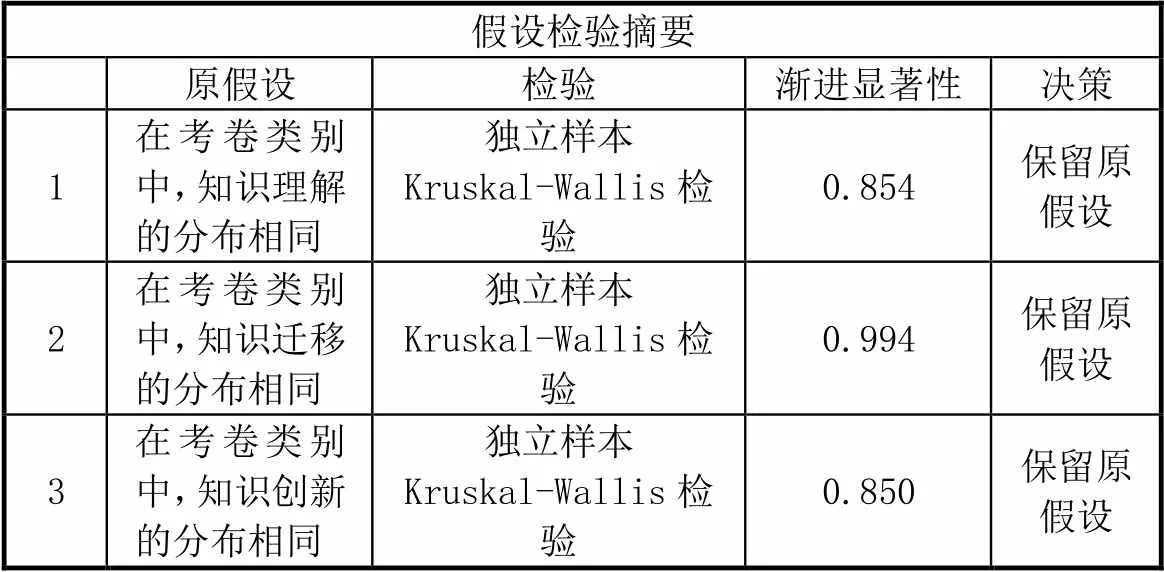
表3 3份試卷中3個水平權重分布差異的顯著性檢驗

表3中漸進顯著性均大于0.05，因此保留原假設，即3份試卷中，知識理解、知識遷移、知識創新三水平的分布沒有顯著性差異．即便新舊高考有著制度上的區別，但它們均以立德樹人、服務選才、引導教學為考查目的，也都遵守著基礎性、綜合性、應用性、創新性的考查要求[15]．因此，盡管細化到單個數學核心素養的每個水平時，3份試卷的考查不盡相同，但3者都能夠較為全面地考查到六大數學核心素養，同水平下的總體分布也沒有顯著性差異．由此可知中國高考的改革并非一蹴而就，而是注重循序漸進，逐步在學科中滲透核心素養，推進改革，引導教學．

4 結論與啟示

4.1 結論

高考以評價促進發展，愈發注重學生數學核心素養的培養．總體來看新舊高考對核心素養的考查都較為全面，根據對2021年新高考Ⅰ卷與2020年全國Ⅰ卷的分析可知，六大數學核心素養中考查比重較高的是數學運算素養、邏輯推理素養與直觀想象素養，平均權重分別為：41.7%、26.9%、15.3%，這3者是學生數學思維形成的重要基石，也是新舊高考考查的重點，多數題目中都會涉及到對它們的考查．

新舊高考對同水平數學核心素養的總體分布沒有顯著性差異．新高考卷中知識理解、知識遷移、知識創新三水平考查的權重分別為41.9%、45.3%、12.7%，文科卷與理科卷中考查的權重均值為38.3%、48.7%、13.2%，可以看出，新舊高考都是對知識理解和知識遷移水平的考查較多，知識創新水平的考查較少．知識理解和知識遷移水平的題目具有一定的基礎性，而知識創新水平的題目往往會要求學生提出創造性的解法，這個過程能夠很好地體現出學生對數學知識的把握，對數學學科的理解，同時對學生的要求也比較高，具有很好的區分度．

新高考卷注重在理科卷和文科卷之間取得平衡，科學把控難度．根據表2中的數據可知，在單個數學核心素養的考查中，新高考卷多處介于理科卷和文科卷之間，如在有一定難度的知識創新水平上，數學運算素養的考查權重分別為：理科卷5.7%、文科卷2.1%、新高考卷3.7%，邏輯推理素養的考查權重分別為：理科卷10%、文科卷5%、新高考卷5.7%．新高考對核心素養難度的設置更加合理，兼顧對不同水平和不同思維模式學生的考查，使評價合理有效．根據以上研究結論可以獲得如下對高考命題改革與教育教學方面的啟示．

4.2 啟示

（1）服務選才，堅持素養導向．

高考服務于高校選才，同時也肩負了育人功能．中國教育以立德樹人為根本任務，培養德智體美勞全面發展的時代新人，這必然要打破“唯分數論”，突出學生核心素養的培養．學生不僅要能夠運用所學知識解決卷面上的題目，更要能夠將知識轉化為解決現實問題的能力．因此在高考試題的命制中應當合理設置知識理解、知識遷移、知識創新三水平的考查權重，適當提高知識創新水平的占比，減少需要死記硬背的考查內容，以評價促進發展，推動落實對學生學科核心素養的培養．

（2）循序漸進，穩步優化改革．

教育部考試中心指出，新高考過渡時期的重點考試內容來自《高中實驗版數學課程標準》和《高中數學課程標準（2017年版）》中的公共部分[17]，因此在知識載體上，新舊高考的內容同宗．根據對新舊高考核心素養考查情況的分析可知，新舊高考對學生數學核心素養的考查都較為全面，且總體考查水平沒有顯著性差異．因此高考改革并非大幅度地改動考卷的內容和難度，而是基于課程標準，小步前進，創新的同時求穩，逐步優化試卷結構，科學而精準地對學生所積累的素養進行測量．

（3）因材施教，適應考核形式．

新高考貫徹“低起點，多層次，高落差”的調控策略[18]，創新題型設計，有效提高區分度．如新高考卷中多選題和結構不良題目的設置，多選題分值設置為全部選對得5分，部分選對得2分，選錯不得分．這種設計能夠更加準確地判斷考生對數學概念的掌握程度、對數學方法的熟練程度以及考生的核心素養水平，不同選項對核心素養的考查呈現出一定的梯度，既能夠讓低水平學生得到基礎分，又能夠區分出高水平學生．在這種趨勢下，教師要對學生的能力有全面的了解，因材施教，牢固低水平學生的基礎，提高高水平學生的做題速度．

（4）把握本質，滲透數學思想．

新高考注重平衡文理科卷，對難度的調控更加科學，相比于對高技巧性題目的考查，更加注重對學生數學思維的評價．日常教學中教師的知識及教法會對學生的學業表現及學習態度等方面產生較深的影響[19–22]，因此，為讓學生更好地應對新高考，教師應當深入理解高考改革的方向和重點考查的內容，注重對數學本質的把握，發掘教材中的核心素養元素，合理設計數學活動．教學中要注重數學思想方法的滲透，注重學生數學關鍵能力的發展，注重學生批判思維的形成，避免機械刷題，避免盲目加大或削弱學生日常練習的難度，培養學生的創新意識、探究意識和獨立思考的能力，落實數學核心素養的培養．

[1] 姜鋼．《實施意見》：我國新一輪高考改革的綱領性文件[J]．中國考試，2017（2）：1–4．

[2] 國務院．國務院關于深化考試招生制度改革的實施意見[EB/OL]．（2014–09–04）[2021–07–30]．http://www.gov.cn/zhengce/content/2014-09/04/content_9065.htm．

[3] 中華人民共和國教育部．教育部關于全面深化課程改革落實立德樹人根本任務的意見[EB/OL]．（2014–04–08）[2021–07–30]．http://www.moe.gov.cn/srcsite/A26/jcj_kcjcgh/201404/t20140408_167226.html．

[4] 任子朝，陳昂，趙軒．數學核心素養評價研究[J]．課程·教材·教法，2018，38（5）：116–121．

[5] 中華人民共和國教育部．普通高中數學課程標準（2017年版2020年修訂）[M]．北京：人民教育出版社，2020：4，100–106．

[6] 武麗莎，朱立明．高中數學學科核心素養：生成機制與培養路徑[J]．數學教育學報，2021，30（4）：25–29．

[7] 路江江，王亞妮．高中數學教育中如何培養學生的數學核心素養——王尚志教授訪談錄[J]．數學教育學報，2021，30（2）：67–70．

[8] 邵貴明，胡典順，柳福祥．論數學核心素養在高中數學課堂落地生根——以人教版高中“對數”教學為例[J]．數學教育學報，2020，29（6）：46–50．

[9] 喻平．基于核心素養的高中數學課程目標與學業評價[J]．課程·教材·教法，2018，38（1）：80–85．

[10] 喻平．數學核心素養評價的一個框架[J]．數學教育學報，2017，26（2）：19–23．

[11] 崔志翔，楊作東．義務教育階段一個數學核心素養的評價框架[J]．數學教育學報，2021，30（5）：47–52．

[12] 李華，胡典順．基于數學核心素養評價框架的試卷測評研究——以2019年高考全國卷為例[J]．數學教育學報，2020，29（2）：18–23．

[13] 張玉環，周俠，陳爽．核心素養視角下中法高考數學試題的比較研究——基于2015—2020年中國和法國高考數學試卷[J]．數學教育學報，2021，30（1）：42–48．

[14] 張奠宙，李士锜，李俊．數學教育學導論[M]．北京：高等教育出版社，2003：54．

[15] 于涵，鄭益慧，程力，等．高考評價體系的實踐功能探析[J]．中國考試，2019（12）：1–6．

[16] 任子朝，趙軒，關丹丹，等．圖形分析法在高考試題評價中的應用研究[J]．數學教育學報，2021，30（1）：37–41．

[17] 教育部考試中心．聚焦核心素養考查關鍵能力——2021年高考數學全國卷試題評析[J]．中國考試，2021（7）：70–76．

[18] 教育部考試中心．以評價體系引領內容改革 以科學情境考查關鍵能力——2020年高考數學全國卷試題評析[J]．中國考試，2020（8）：29–34．

[19] 郭衎，曹一鳴．知識與信念：基于學生表現的教師核心素養研究[J]．數學教育學報，2021，30（4）：1–5．

[20] 趙思林，潘超．中學數學教師核心素養及構成要素[J]．數學教育學報，2021，30（2）：48–54．

[21] 李保臻，馬登堂．基于小學生數學運算素養培育的課例比較研究——以“三位數乘兩位數”的同課異構為例[J]．數學教育學報，2021，30（2）：8–13．

[22] 范會敏，陳旭遠，張娟娟．基于精準框架的素養導向數學課堂教學評估——以全國小學數學（人教版）核心素養示范課教學視頻分析為例[J]．數學教育學報，2021，30（2）：20–25．

A Comparative Analysis of New and Old College Entrance Examination Based on Mathematical Key Competencies——Taking the 2021 New College Entrance Examination Volume I and the 2020 National Volume I as Examples

LI Zi-zhan, HU Dian-shun

(College of Mathematics and Statistic, Central China Normal University, Hubei Wuhan 430079, China)

The college entrance examination in the new era pays more attention to the measurement and evaluation of students’ mathematical key competencies. Based on the classification of mathematical key competencies level in the curriculum standards and Yu Ping’s description of the three levels of knowledge understanding, knowledge transfer and knowledge innovation, an evaluation index framework for mathematical key competencies is established. And based on this, the key competencies examined in the 2021 New College Entrance Examination VolumeⅠand the 2020 National VolumeⅠare assigned. Quantitative analysis of the assignment shows that the old and new college entrance examinations have higher weights in the three types of literacy: mathematical operation, logical reasoning, and intuitive imagination; they have different emphasis on the test level of single literacy, but there is no significant difference in the overall distribution of the same level, knowledge understanding and knowledge transfer level occupying a higher proportion; the new college entrance examination does not distinguish between liberal arts and sciences, and the difficulty adjustment is more scientific. Based on these results, the following enlightenment can be obtained: the proposition of the college entrance examination should adhere to the literacy orientation and steadily optimize the reform; the teaching should adapt to the assessment form and penetrate mathematical ideas

mathematical key competencies; college entrance examination reform; the paper of new college entrance examination

2022–02–01

教育部人文社會科學研究規劃基金項目——中小學核心素養測評的模型建構與實證研究（19YJA880012）；中央高校基本科研業務費項目——新高考分省市命題分學科質量評價指標體系研究（CCNUTEI2021-13）

李子瞻（1996—），女，安徽亳州人，碩士生，主要從事數學課程與數學教學研究．胡典順為本文通訊作者．

G632

A

1004–9894（2022）03–0026–06

李子瞻，胡典順．基于數學核心素養的新舊高考比較分析——以2021年新高考Ⅰ卷與2020年全國Ⅰ卷為例[J]．數學教育學報，2022，31（3）：26-31．

[責任編校：周學智、陳漢君]