高考概率與統計試題的統計與分析——以2021年全國課標卷為例

李亞瓊，潘禹辰，徐文彬，錢詣文，張海燕

高考概率與統計試題的統計與分析——以2021年全國課標卷為例

李亞瓊1，潘禹辰1，徐文彬1，錢詣文2，張海燕3

（1．南京師范大學 課程與教學研究所，江蘇 南京 210079；2．南京師范大學 數學科學學院，江蘇 南京 210023；3．赤峰學院 教育科學學院，內蒙古 赤峰 024000）

基于2021年6套課標卷中概率與統計試題的統計與分析，從情境設置、知識考查、統計素養、綜合難度4個維度進行定量和定性分析，研究發現：試題強調問題情境的創新融合，關注基礎知識的變式考查，滲透統計素養的應用考查，凸顯了概率統計的綜合考查．具體表現為，注重由實際問題抽象出統計概念，并能用統計數據進行分析，以此進行統計判斷；運用概率統計的視角去分析問題、構建模型、計算結果及依據結果提出決策，凸顯運用統計思維解決問題的能力．結合全國課標卷概率統計試題特點，基于高考對教學的導向作用，概率統計專題教學需要重視：關注新舊課標的變化，落實知識整體；兼顧情境設計與概念理解，適應趨勢要求；優化概率與統計教學，提升學生統計素養．

全國課標卷；概率統計；綜合難度；統計素養；統計與分析

1 問題提出

傳統概率統計教學中，往往重視概率統計的科學工具性價值，而忽視其文化內涵與育人功能[1]．《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱2017新課標）將“數據分析”作為高中數學課程目標中培養學生所必備的數學素養之一，這既凸顯高中課程中概率統計內容的教學價值，也是對概率統計的育人價值提出更高的要求．高考實行不分文理科的改革后，數學科考試中概率統計的定位、考查內容和形式以及考生群體和水平隨之發生變化，所以研究概率統計試題、試卷結構和難度要求等[2]對教學有較大的價值．結合試題研究回歸課標要求、落實教學目標、開展有效教學[3]，發揮新高考數學科新要求對中學數學教學起到積極導向作用．

已有研究基于2011—2020年10年全國卷，從考查總分、考查知識、試題特點和命題導向4個方面對概率統計試題特點進行了統計與分析[4]．這里將在前面研究的基礎上，結合2021年新課標I、新課標II卷、全國甲卷（文、理）、全國乙卷（文、理）共6套試卷，繼續對概率與統計部分進行統計分析，試圖梳理出2021年課標卷中概率與統計試題的特點，在回應前面研究的基礎上，批判性地再分析教學啟示部分．

2 分析維度

采用定性與定量研究相結合的研究方法，分別從情境設置、知識考查、統計素養、綜合難度4個維度[5]對試題進行統計分析，以期分析概率與統計試題的命題特點．

2.1 情境設置

新課標在劃分學業質量水平時，第一個考慮了“情境與問題”，可見對數學學科素養的考查需要在一定情境中進行[6]．通過對2021年課標卷中概率與統計試題的研究發現：試題重視情境創設和問題提出，這與新課標的要求相契合，也是接下來需要繼續關注的地方．依據2017年新課標中對情境的維度劃分（科學情境、數學情境、現實情境）[7]進行問題情境設置的統計與分析．

2.2 知識考查

對概率與統計知識的梳理有利于把握核心知識，明確考查方向．基于2019年高考考試大綱及2017新課標對概率與統計知識進行整理和歸納，將概率統計知識分為8個一級知識和22個二級知識，并對其進行編碼[5]（具體內容見表1）．如B3指的是考查樣本估計總體中的用樣本數據特征估計總體，G4指的是考查隨機變量中的正態分布．

2.3 統計素養

何為統計素養？李金昌教授認為，統計素養就是人們掌握統計基本知識的程度、統計理論方法的水平及運用統計方法解決現實問題的能力，包含統計知識、統計方法、統計思維等[8]．統計素養的內涵不僅包含由統計知識、統計觀念等知識技能；還包括統計判斷、統計推斷等統計思維；也還包含對概率的要求，統計素養的形成具有層次性．Gal對統計素養的界定是：（1）解釋和批判性地評估在不同背景下可能遇到的相關統計信息、有關數據的論證或隨機現象的能力；（2）討論或傳達對此類統計信息的反應能力，例如他們對信息的理解、對信息含義的看法，或是對給定結論的可接受性關注[9]．Watson提出統計素養的3層次結構：理解基本的統計術語；理解出現在社會背景中的術語；能夠質疑在脫離適當統計論證的背景下提出的主張[10]．

表1 概率與統計知識考查編碼

基于表2[11]對2021年課標卷中概率統計試題側重考查的統計素養進行分析．其中，表2中S1和S2對應“理解用于統計決策的術語”，S3和S4對應“解釋在背景中呈現的術語”，S5和S6對應“質疑在脫離適當統計基礎的背景中的陳述”．

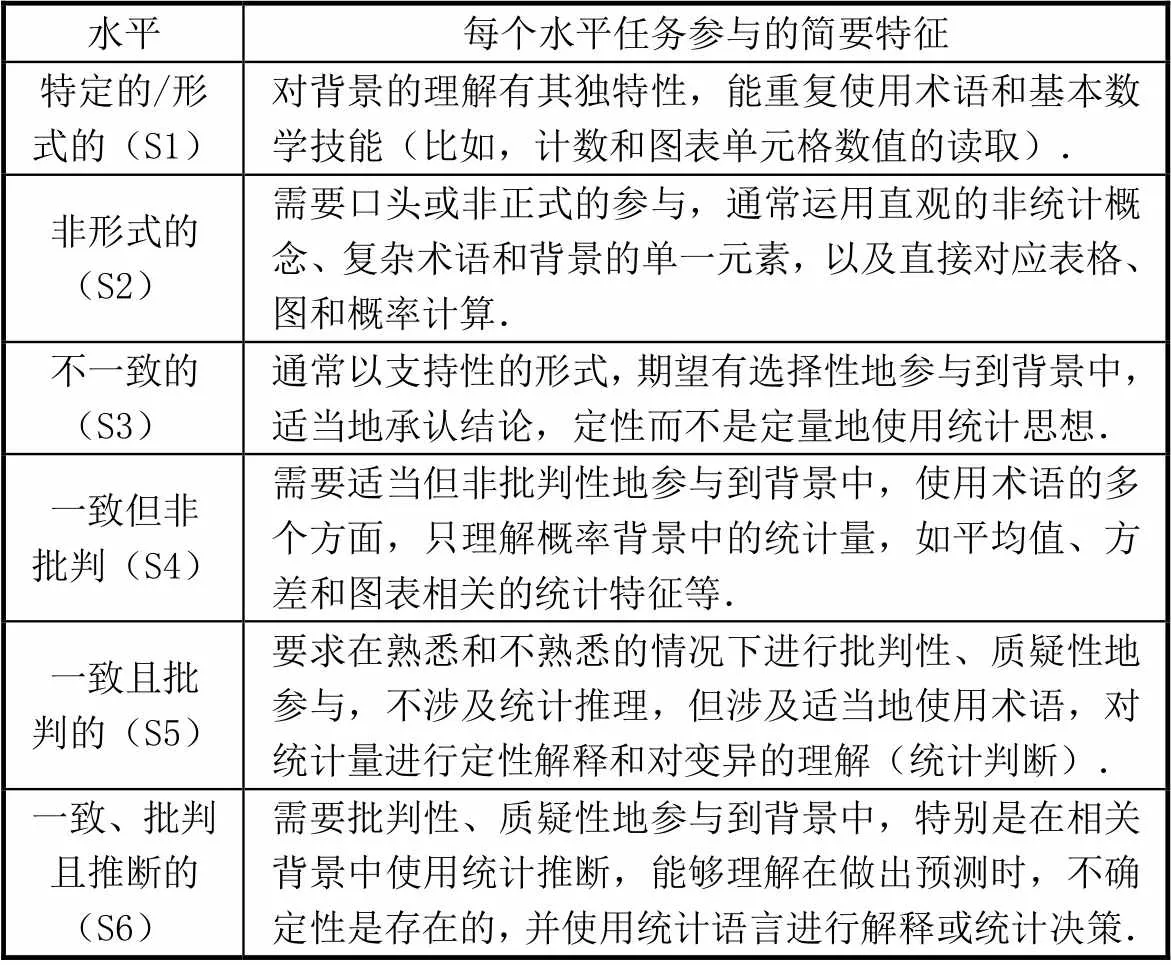
表2 統計素養水平劃分

2.4 綜合難度

高考試題難度是試卷評價的重要特點之一，對于試題難度的分析，較多學者采用鮑建生綜合難度模型，該模型包含“探究”“背景”“運算”“推理”“知識含量”5個難度影響因素[12]．在標準化測試中該模型應用效果需要改善，因此武小鵬和孔企平（2020）在此基礎上進行了改進，增加“是否含參”“思維方向”兩個維度，鑒于評級模型維度的合理性和全面性，采用武小鵬和孔企平構建的綜合難度模型對2021年課標卷概率與統計試題難度進行分析評估[13]．由于原模型是分析整套試卷的，基于此進行調整并應用于分析某道題的難度系數（具體詳見表3）．

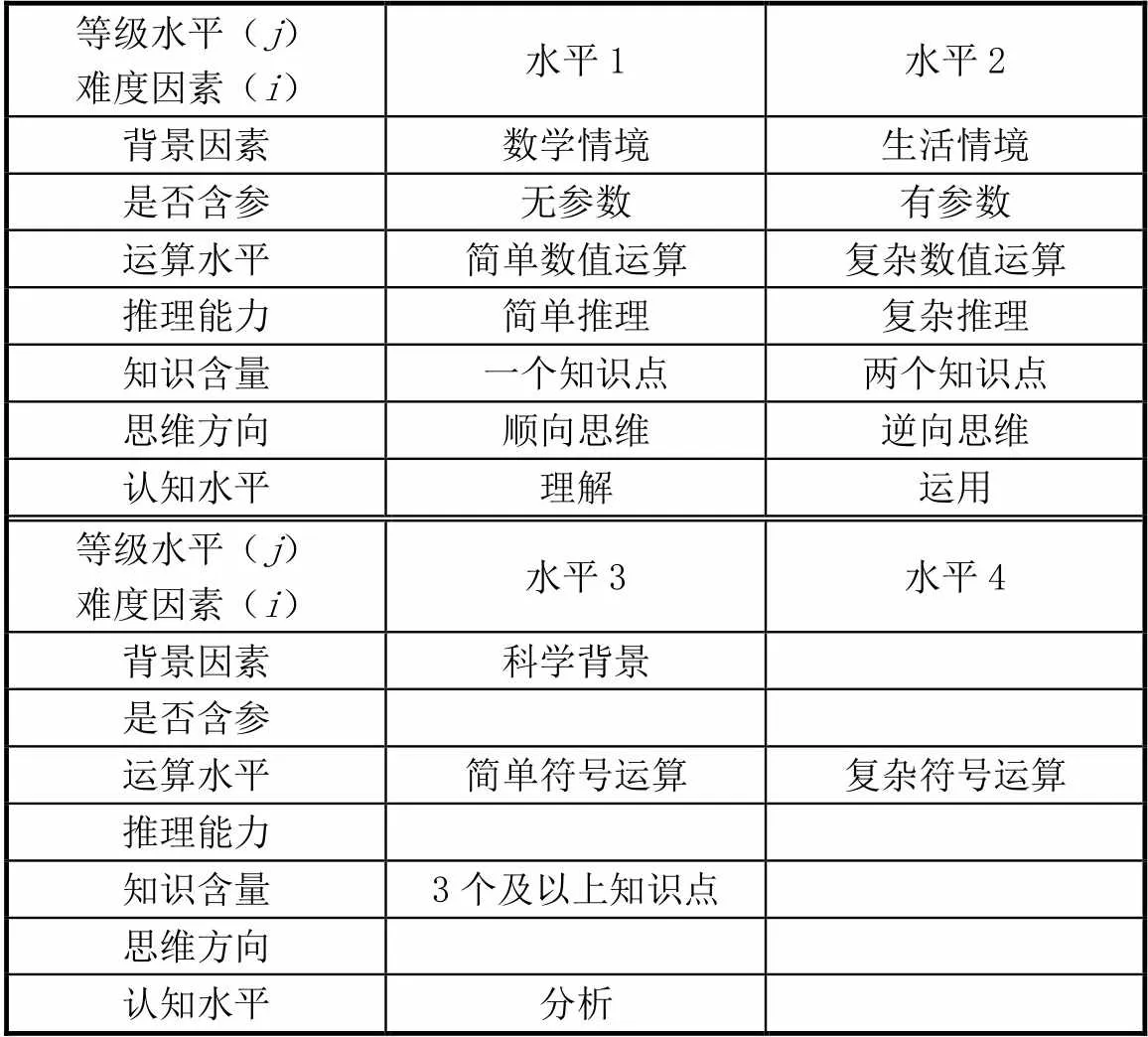
表3 難度因素等級劃分

注：記第個因素第個等級為，n為第個等級的權重，分別取1、2、3、4．則該題的等級難度系數為：

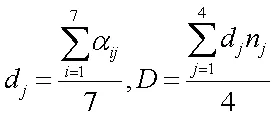
3 試題特點分析

2021年6套全國課標卷共考查16道概率與統計試題（文理卷中題目相同均重復計算），基于表3的分析框架，梳理出每道題的綜合難度系數（具體詳見表4）．總體來說（從表4中可以看出），概率統計考查題量為選填題考查1—2題（2021年課標卷中填空題均未考查概率統計），解答題考查1題，基本處于中檔題．除了新高考I卷概率統計選擇題處在第8題（即單選最后一題），新高考II卷中概率統計解答題在21題（處于解答題壓軸題），其余4套試卷中概率統計試題處于選填題（新高考I、II卷中，1—8題為單選，9—12題為多選）中檔位置，解答題位于17題或18題．總體來說，概率與統計試題情境設置綜合，試題難度適中，試題總體具有“基礎性、綜合性、應用性和創新性”的特點．

3.1 基于情境的創新融合 關注基礎知識的變式考查

這里分析的6套試卷16道概率統計題（由表4知）中，生活情境考查10次，科學情境考查2次，數學情境考查4次．可以看出選填題及解答題以生活情境為背景較多，主要考查學生能將現實背景抽象為統計語言，基于此去分析問題和解決問題，這也充分體現了概率統計與現實緊密相關．在大數據時代背景下，概率與統計的理論與應用研究更有價值．如，新高考I卷第18題以“一帶一路知識競賽”為情境，重視考查離散型隨機變量分布列及期望，關注學生的數學抽象及統計判斷的能力．新高考II卷第21題取材于微生物繁殖的問題情境，體現概率與統計在生命科學中的應用．該試題考查學生的數學抽象、數學建模、邏輯推理等學科素養，重點考查學生概率、數列、函數與方程等知識的綜合應用能力，體現概率統計試題重視問題情境的創新考查，凸顯試題具有“綜合性、應用性和創新性”的特點．

同時，全國卷對概率統計的考查重基礎知識、基本經驗、基本技能及基本方法．從知識維度來看（詳見表1和表4），概率與統計選填題一般只考查1～2個知識點，考查要求都以概念理解及簡單應用為主，部分題目融入了函數、不等式、幾何等知識點．比如2021年乙卷理科第8題利用線性規劃的知識建立圖形，再考查幾何概型的簡單運用．概率與統計解答題一般考查2個知識點及以上，對學生的應用和分析能力要求較高．高頻考查知識點一般集中于隨機變量和統計分析，偏重于考查學生在復雜情境中的數學抽象和數學建模能力．

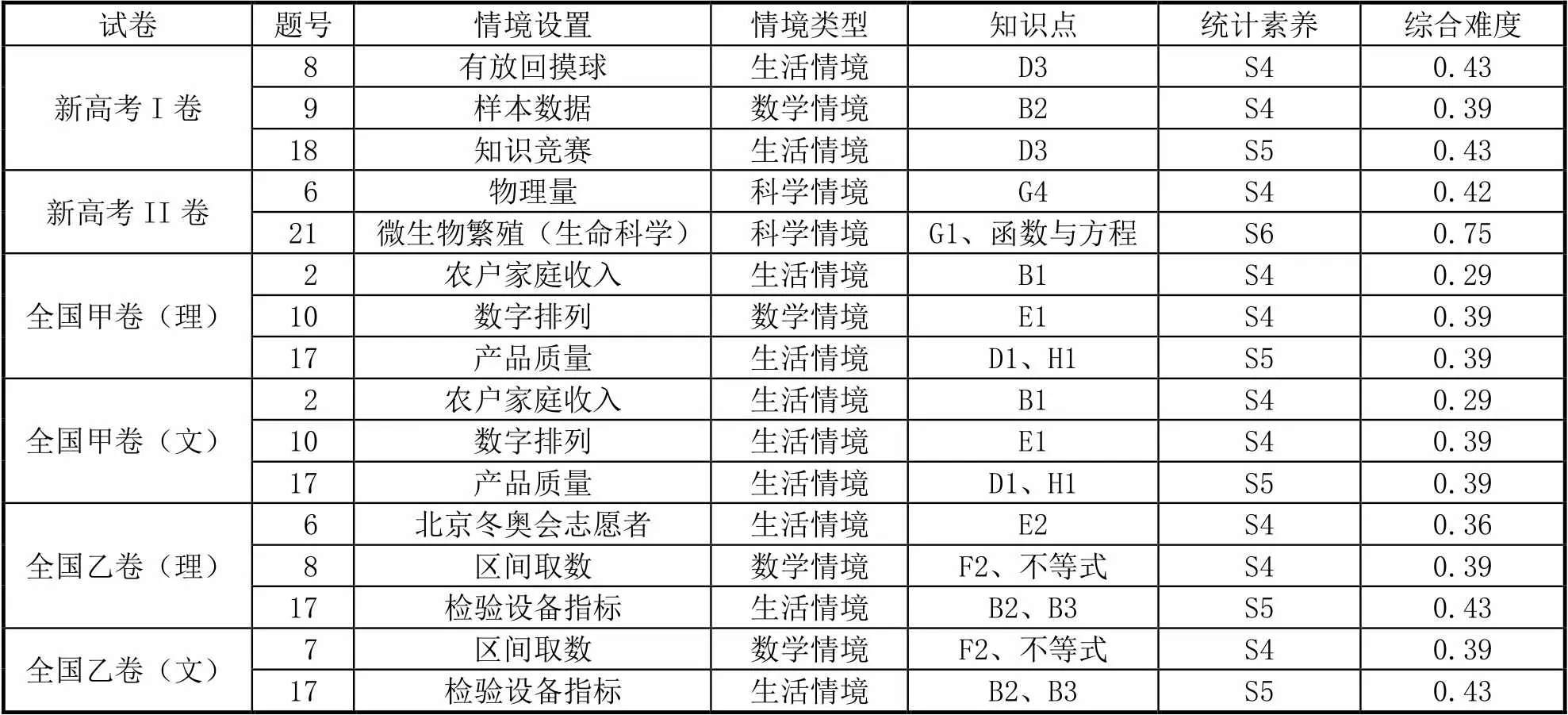
表4 2021年課標卷概率與統計試題（選填題及解答題）統計

試題基本貼近高中生的知識水平和生活體驗，在基本知識上推陳出新，體現命題源于基礎而又高于基礎的特點．比如，2021年新高考I卷第8題以有放回摸球為背景考查隨機事件的獨立性，該題在命題設置上雖屬于單選題最后一題，但試題難度適中．新高考II卷第6題以某物理量為背景考查正態分布基本概念的理解，體現基礎知識的靈活運用．2021年乙卷理科第6題以“冬季奧運會”為背景考查計數原理，2021年新高考I卷第18題以知識競賽為素材考查離散型隨機變量分布列及期望，2021年甲卷文理科第2題都是以“農戶家庭收入”為背景考查對頻率分布直方圖的分析，2021年甲卷文理科第17題是以“產品質量”為背景考查獨立性檢驗（2′2列聯表）……這些試題均通過對基礎知識的重新變式或拓展，賦予時代氣息，體現課標卷的設計理念，命題尊重了不同學生的思維差異，體現人文教育精神．

3.2 滲透統計素養的應用考查

學科思維是核心素養中的最高層[14]，所以統計素養可以理解為不僅含有數學層面的關于數據、概率等的思維，還應當包含指向現實意義的運用統計解決問題、理解世界的方面．那么高考題所要考查的應是學生能否用統計思維去思考和解決（現實）問題，以及基于此進行統計判斷或決策．而對統計的考查側重于用樣本數字特征對總體進行估計，考查樣本估計總體的統計思想[15]．2021年全國課標卷概率與統計試題注重考查學生能根據實際問題抽象出統計概念，并能用統計數據進行分析，以此進行統計判斷，將數學解答轉化成對現實對象的分析．

概率統計的知識與現實生活和科技發展緊密相關，具有較強的理論性和應用性，是數學模型的重要載體[16]．從統計素養維度分析來看（具體詳見表4），2021年課標卷中概率與統計試題對統計思維的考查主要側重于S4和S5水平．其中，16道題中考查S4水平的有10次，考查S5水平的有5次，新高考II卷第21題考查S6水平．由此可以看出，概率與統計試題強調，結合現實情境使用統計術語計算統計量并理解統計量，有時需要對統計量進行定性的解釋．比如新高考I卷第18題，需要學生從知識競賽的背景下，計算出相應的概率及數學期望，并要求學生去判斷“先答哪一類題”累計積分的期望最大，這其實是考查學生結合統計量進行統計判斷的能力．再比如新高考II卷第21題結合離散型隨機變量的數學期望表達式及函數與方程的思想去驗證結論，并利用計算結果去分析結論的實際含義及依據數據分析做出初步的統計判斷．在強調不確定性前提下，使用統計語言對結論進行解釋或統計決策，這其實是考查學生S6水平的統計素養．解答題或選填題多以現實情境為背景，運用統計視角分析問題、構建模型、計算結果及依據結果提出決策，這一過程考查學生運用統計思維解決問題的能力．

3.3 凸顯概率統計的綜合考查

由表3可以看出，2021年課標卷中概率統計試題的綜合難度系數都在0.5左右．需要說明的是，此處的綜合難度系數模型不同于一般意義上試題難度的考量標準，但能充分考慮到不同因素對測試試題考查因素的影響，其中n為第個等級的權重，分別取1、2、3、4，可能不同學者采用不同的賦值方式，但在同一賦值標準下計算出的綜合難度系數，從某種程度上可以對比出同一類型試題的綜合考查情況．

為了分析6套試卷概率統計試題的難度特征，對同一年的選填題難度取平均值（解答題不變），并繪制統計圖．由圖1可知，概率統計選填題的綜合難度在0.4左右，解答題的難度系數在0.5左右，而難度系數的偏度值為1.279，數據呈明顯的右偏態，這表明概率與統計試題難度偏低（與前5年全國卷概率統計試題綜合難度系數比較）[5]．其中新高考II卷的解答題（內容詳見例*）難度系數為0.75，其難度系數最高．該題位于解答題壓軸題位置，以生命科學中微生物繁殖為問題情境，情境容易理解，學生較容易抽象出統計概念，并計算出()．難點在于第二問，其運算過程含有參數，考查學生綜合應用概率、數列、函數與方程的知識和方法解決問題的能力．第三問需要結合得到的結論，再回到情境本身，運用統計判斷去解釋結論的實際含義，即一個微生物個體繁殖下一代的個數不大于1時，會臨近滅絕；個數大于1時，不會滅絕．這也強調了，對概率的考查不應只停留在計算的層面，需要能夠利用計算結果為決策提出關鍵性的依據驗證，并能為解決問題提供較為科學的決策建議，體現了概率與統計的綜合性和應用性的考查要求．

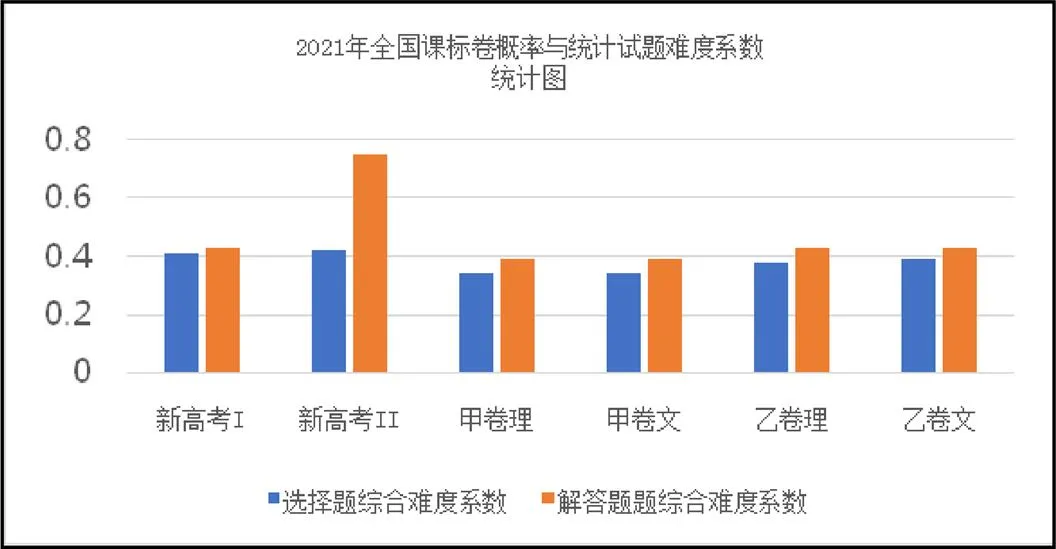
圖1 選填題與解答題綜合難度系數統計

例*：（新高考II卷第21題）一種微生物群體可以經過自身繁殖不斷生存下來，設一個這種微生物為第0代，經過一次繁殖后為第一代，再經過一次繁殖后為第2代……，該微生物每代繁殖的個數是相互獨立的且有相同的分布列．設表示1個微生物個體繁殖為下一代的個數，(=)=p(=1, 2, 3)．

（1）已知0=0.4，1=0.3，2=0.2，3=0.1，求()；

（2）設表示該種微生物經過多代繁殖后臨近滅絕的 概率，是關于的方程：0+122+33=的最小正實根，求證：當()≤1時，=1；當()>1時，<1；

（3）根據你的理解說明（2）結論的實際含義．

結合表3和表4可以看出，概率統計試題側重考查學生思維的靈活性，有時需要學生運用“正難則反”的逆向思維去解決問題．比如甲卷文理卷第10題中，求2個0不相鄰的概率，可以從對立命題去考慮2個0相鄰的概率，這樣可以優化解題過程，提高解題效率．當然，試題考查難度提升的標志之一便是題目中設有參數，如新高考II卷第21題第二問便增加了參數，這在一定程度上讓學生產生了恐懼心理．當然這樣的考查符合壓軸題的難度要求，同時也體現知識的交互性，需要學生結合多個知識點及思想方法去分析問題解決問題，體現了高考課標卷對概率統計考查的綜合性．

總體來說，全國課標卷對概率統計命題趨于綜合化，其重視情境的創新融入、基礎知識的變式考查和統計素養的應用考查．試題注重與情境相結合，突出概率統計在解決實際問題中的作用．知識點考查上，加大了學科間的知識融合命題，注重概率與函數、概率與不等式、概率與數列等交匯知識的融合考查．統計素養的應用體現滲透于隨機思想、抽樣思想、或然與必然思想[17]的理解及運用，側重用概率或統計模型來表達隨機現象的統計規律，用數據呈現的規律來解釋隨機現象及對抽樣方法的統計意義的理解．

4 教學啟示

結合分析維度的設置及試題特點的分析，剖析高考試卷的導向教學作用：教學中，需要結合新舊課標的變化，落實知識整體；需要兼顧情境設計與概念理解，適應趨勢要求；通過優化概率統計教學，提升學生統計素養．

4.1 關注新舊課標變化 落實知識整體

由表1的概率統計知識的梳理及表4中概率統計知識的考查情況可知，概率統計選填題和解答題的綜合難度系數在0.5左右，難度適中（詳見圖1），但對概率統計知識點的考查具有系統化、關聯性及層次性的特點．而這與2017新課標的理念不謀而合，其中提到，教師要以學科素養為導向，明晰學科素養在內容體系形成中表現出的連續性和階段性，引導學生整體上把握課程．教學建議中指出，整體把握教學內容，才能促進學科素養的連續性和階段性發展[7]．然而，高中概率統計知識分布于必修和選擇性必修中，知識內容分散與新課標的整體要求相矛盾．再者，學生認知能力的局限性，教材編寫時需要將知識分解到各個年段，教材編寫的限制帶來教學內容的分散性，而課時的限制又帶來教學過程的間斷性．但概率統計知識結構具有內在統一性，教師需要處理好概率統計知識的整體把握和學生的局部認識之間的矛盾，從而落實知識教學的整體性．

學生在答題時會出現符號表達不準確或概念理解不到位，其根本原因在于知識掌握不系統，這就需要高中概率統計教學中關注知識整體性，讓學生在理解概念的基礎上去掌握相關性質．李亞瓊、徐文彬（2021）提到，概率統計知識的結構層次不是概率和統計的并列式呈現，其橫向需要關注必修內容和選擇性必修內容的銜接，體現知識的螺旋式上升，縱向需要關注概率與統計知識的內在生成關系（具體詳見圖2）．比如，其中“整理、分析數據”和“表達與解釋”共同為研究“樣本估計”和“相關關系”作鋪墊[4]．了解知識整體結構圖是教師落實概率與統計整體教學的邏輯起點，教師需要厘清知識間的聯系以及同一部分內容中知識的關聯性和層次性，最后呈現出結構化知識體系，再用于教學實踐．

4.2 兼顧情境設計與概念理解 適應趨勢要求

由表4可以看出，概率與統計的情境設置注重生活情境的創新融入（其中生活情境考查10次，占比62.5%），蘊含時代性及多元文化性．結合2011—2020年全國卷概率統計試題情境設計的變化趨勢[4]及文中概率統計情境設置的分析，可以看出：如何引導學生從豐富的問題情境出發，運用概率與統計的思想與方法去解決問題，這是關鍵所在．即引導學生通過情境抽象出信息與問題，從而運用統計思維去解決問題．高中階段概率與統計的學習中，學生大多停留在簡單機械運用統計符號或統計概念解決問題，導致統計符號或概念的理解過程缺乏系統性和準確性．

統計目的是為了解決問題，而統計背后的基本概念（也被稱為“重要思想”）是教學重點．盡管對于“基本概念具體包括哪些”還存在爭議，且基本概念的表示形式也有所不同，但基本上都涵蓋了數據、期望、分布、樣本和抽樣等思想．統計學家陳希孺教授曾提到：“關于抽樣、數據、誤差、平均值、標準差、統計規律、統計相關性、大數律等內容，是與我們現實生活緊密相連的基本概念．”[18]Watson等人（2013）凝練出的5個與統計相關的重要概念，包括期望、分布、隨機性和非正式推斷，并強調了這些重要思想在整個統計中是緊密相連的[10]．2017新課標中加大了概率統計的教學學時，這不僅體現在高中必修選修內容中，也已經滲入義務教育數學課程（將“數據分析觀念”作為十大核心詞之一）．培養“學生的統計觀念”目標的課程發展理念，預示概率與統計的教學需要關注學生統計概念的理解，這也是對統計教育變化趨勢的回應．

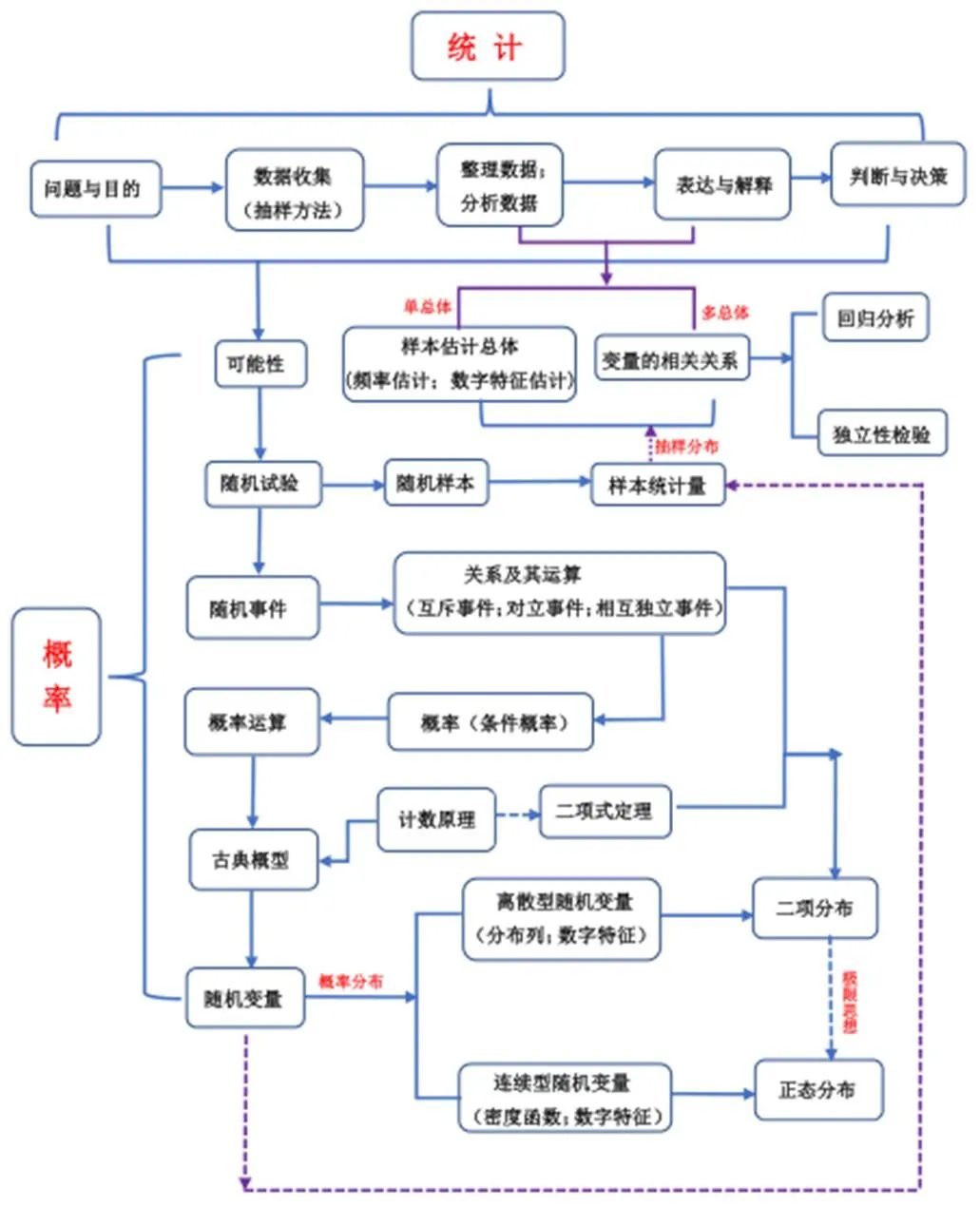
圖2 2017版課標中概率統計內容的整體結構

4.3 優化概率與統計教學 提升學生統計素養

從表2統計素養的水平劃分及表4中統計素養考查的數據可以看出，高考試題在概率統計知識設置上，關注對統計素養S4的考查，對S4考查有8次，占比50%（由表4可知）；側重對統計素養S5的考查，對S5的考查有5次，占比30%左右（由表4可知），重視理解概念背景下的統計量，關注考查對統計量進行定性解釋和統計判斷．這些數據表明，試題越來越關注統計概念本質理解及統計素養的培養．對高中生來說，他們需要明確統計概念，掌握系統的統計知識，培養有層次的統計素養，這就對概率統計教學提出更高的要求．伴隨著學生群體的多樣化，教師面臨著為不同知識和技能水平的學生提供差異化概率統計教學[19]．很多高中教授概率統計的教師并未系統學習過概率統計專業知識，如何讓這類教師做好統計教學的準備，是當前教師專業發展中一個迫切需要解決的問題．無論是滿足統計學習、教學的需要，還是促進教師自身的發展需求，概率與統計教學都應以統計素養為核心目標．Scheaffer等人在1998年曾提及中學培養學生統計素養的專題內容需包括：數感；理解變量；讀懂統計表和統計圖；設計調查或實驗獲取樣本，收集數據的方法，問卷調查的設計等；數據分析；概率與統計的聯系，顯著性檢驗的理論背景等；統計推斷等[20]．與此相比，中國統計教育內容在課程設計上偏重于書本知識的學習，忽視實踐應用知識的學習，忽視學習過程中常見認知錯誤的矯正，這樣的忽視必然會影響學生統計素養的培養[18]．

數學教材中的例、習題偏重于統計量的計算和圖表繪制和解讀這類基本知識的練習，而非側重于對統計判斷、決策、質疑等統計素養的考查．比如，通過設置適當的情境讓學生理解統計量對決策的作用，通過讓學生根據給定結論設計調查活動進行檢驗，從而培養其對現實數據的質疑與統計論證能力．此外，對統計實踐完整過程的重視沒有在評估試題中得以體現，一般為碎片式的局部考查，可以嘗試采用其它多樣化的評價形式，如調研報告、主題匯報等，這能給學生提供發現、提出、分析、解決統計問題的機會．目前教學中，統計素養尚未引起足夠的重視，且大多數統計教學評價仍限于借助筆紙測試來反映教學效果．

此外，教師需要多設計真實統計實踐融入教學，就統計實踐本身而言，每一個調查步驟的設計都應蘊涵著對學生統計素養的滲透．單就統計實踐的本質來說，為了體現統計學習的現實意義，需要把現實與統計學中的核心概念相關聯．另外，學生的統計表達也需要被重視，不能固化學生統計表達的呈現．比如新高考I卷第18題，其考查背景為知識競賽，一般學生都有類似經驗，所以理解起來并不困難．干擾學生的因素是如何使用合適的統計符號去準確表達．比如，在回答的可能取值并寫出相應的取值概率時，有學生呈現(=0)=0.2，(=20)=0.32，(=80)=0，(=100)= 0.48．離散型隨機變量的研究前提下，“概率為零”就意味取不到80．該生其實表達的就是的可能取值為0、20、100，這便是很好的研究契機．教學中，教師需要規范引導學生如何更準確理解“概率為0的事件”，并引導學生將自己的理解規范表達，做出準確的判斷．通過這樣的細節引導，可以遷移默化地滲透統計素養的培養．

5 小結

概率與統計教育教學的最終目的是實現公民統計素養的提升，學校教育正為未來一代的發展做好準備．基礎教育階段概率與統計的學習，試圖為高等教育階段的統計教育打下堅實的基礎與補充．如何優化當前基礎教育階段統計教育的質量也是未來研究需要繼續關注的．

[1] 藺云．哲學與文化視角下概率統計課的育人功能[J]．數學教育學報，2002，11（2）：24–26，102．

[2] 任子朝，陳昂，黃熙彤，等．高考數學新題型試卷質量分析研究[J]．數學教育學報，2019，28（1）：1–7，48．

[3] 張定強，裴陽．新高考改革背景下數學試卷與課標一致性研究[J]．數學教育學報，2019，28（4）：55–60．

[4] 李亞瓊，徐文彬．高考課標卷概率統計試題的特點及其教學啟示——基于2011—2020年全國課標卷的分析[J]．數學教育學報，2021，30（6）：13–19．

[5] 廖藝捷，朱展霖，胡典順．近五年高考概率與統計試題的統計與分析——以全國Ⅰ卷（理科）為例[J]．數學通報，2021，60（2）：56–62．

[6] 胡鳳娟．論“概率與統計”在高考中的定位與考查研究[J]．基礎教育課程，2019（15）：14–21．

[7] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2018：30–31．

[8] 游明倫．對統計素養及其培養的理性思考[J]．統計與決策，2010（12）：2，189．

[9] GAL I. Adults’ statistical literacy: Meanings, components, responsibilities [J]. International Statistical Review, 2002，70 (1): 1–51.

[10] WATSON J M. Assessing statistical thinking using the media [M] // GAL I, GARFIELD J B. The assessment challenge in statistics education. Amsterdam: IOS Press, 1997: 107–121.

[11] WATSON J, CALLINGHAM R. Statistical literacy: A complex hierarchical construct [J]. Statistics Education Research Journal, 2003, 2 (2): 3–46.

[12] 鮑建生．中英兩國初中數學期望課程綜合難度的比較[J]．全球教育展望，2002，31（9）：48–52．

[13] 武小鵬，孔企平．基于AHP理論的數學高考試題綜合難度模型構建與應用[J]．數學教育學報，2020，29（2）：29–34．

[14] 李藝，鐘柏昌．談“核心素養”[J]．教育研究，2015，36（9）：17–23，63．

[15] 周遠方，余錦銀．2014年高考“概率與統計、計數原理”專題分析[J]．中國數學教育，2014（7–8）：106–119，127．

[16] 趙軒，任子朝．高考概率統計試題考查目標的沿革與實現[J]．數學通報，2019，58（10）：39–43．

[17] 王雅琪．談高考中概率與統計的考查[J]．數學通報，2016，55（4）：42–46．

[18] 李俊．論統計素養的培養[J]．浙江教育學院學報，2009（1）：10–16．

[19] 張進良，李保臻．大數據背景下教師數據素養的內涵、價值與發展路徑[J]．電化教育研究，2015，36（7）：14–19，34．

[20] BEN-ZVI D, MAKAR K, GARFIELD J. International handbook of research in statistics education [M]. Springer International Publishing AG, 2018: 444.

Statistics and Analysis of Probability and Statistics Test Questions for College Entrance Examination——Taking the 2021 National Curriculum Standard Paper as a Case

LI Ya-qiong1, PAN Yu-chen1, XU Wen-bin1, QIAN Yi-wen2, ZHANG Hai-yan3

（1. Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210079, China;2. School of Mathematical Sciences, Nanjing Normal University, Jiangsu Nanjing 210023, China;3.School of Educational Sciences, Chifeng College, Inner Mongolia Chifeng 024000, China)

Based on the statistics and analysis of the probability and statistics test questions in the six sets of papers in 2021, the test questions are sorted out from the following four dimensions: situation setting, knowledge points, statistical literacy, and comprehensive difficulty. It is found that probability and statistics paid attention to the innovation of problem situations, focusing on the variant examination of basic knowledge, penetrating the application examination of statistical literacy, and thus highlighting the comprehensive examination of probability and statistics. Specifically, it focuses on abstracting statistical concepts from actual problems and can use statistical data for analysis to make statistical judgments; uses the perspective of probability statistics to analyze problems, build models, calculate results, and make decisions based on results, highlighting the use of statistics thinking to solve problems. Combined with the characteristics of the probability and statistics test questions in the national curriculum standard paper and based on the guiding role of the college entrance examination in teaching, the teaching of probability and statistics should focus on the changes between the old and the new curriculum standards, implement the overall knowledge. Teachers should take into account the situational design and conceptual understanding, adapt to the trend requirements, optimize the probability and statistics teaching, and enhance the students’ statistical literacy.

national curriculum standard paper; probability and statistics; comprehensive difficulty; statistical literacy; statistics and analysis

2022–02–08

江蘇省中小學教學研究課題——教師研究的理論思考與模式建構（2021JY14_L390）；江蘇省研究生科研與實踐創新計劃項目——高中數學整體教學設計的模式建構與實踐應用（SJCX22_0506）

李亞瓊（1983—），女，安徽巢湖人，博士生，主要從事高中數學課程與教學研究．徐文彬為本文通訊作者．

G632

A

1004–9894（2022）03–0020–06

李亞瓊，潘禹辰，徐文彬，等．高考概率與統計試題的統計與分析——以2021年全國課標卷為例[J]．數學教育學報，2022，31（3）：20-25．

[責任編校：周學智、陳漢君]