電容驅動型多級感應線圈炮模型簡化

郭燈華， 史鐸林， 關曉存， 管少華， 吳彪

(海軍工程大學 艦船綜合電力技術國防科技重點實驗室，湖北 武漢 430033)

0 引 言

電磁發射裝置將電能轉化為機械動能，利用電磁力推動彈丸加速[1]，提高了炮彈的出口速度，在新型武器系統研究中擁有重要地位。電磁炮按照結構不同分為軌道炮、線圈炮、重接炮[2-3]，其中感應線圈炮結構簡單、設計靈活[4]，通過驅動線圈與電樞之間的電磁力實現炮彈加速，發射過程中電樞與驅動線圈之間無物理接觸，且可控性強，不僅在武器系統中有廣泛應用，還在航天、航空領域擁有廣闊的發展前景[5-8]。

精確的感應線圈炮的控制模型十分重要，雖然感應線圈炮的結構簡單，但是發射過程中的線圈與電樞的耦合使得線圈炮的數學模型復雜。在國內外線圈炮的研究中，都是通過不斷地精確其模型來提升其發射效果。早在20世紀90年代，Sandia國家實驗室開發的WRAP-10[9]、SLINGSHOT[10]以及CEM大學的Axi-coil[11-12]程序建立了同步線圈炮的動態模型仿真以檢驗發射器的性能。除此之外，針對動態過程中各種可能影響發射性能的因素，也有諸多相關模型仿真研究。文獻[13]考慮線圈發射裝置中電樞結構受徑向磁場力的影響，建立了完整的磁流體力學模型，并以此計算出最優的電樞結構，實現了在高能量下使電樞形變最小。文獻[14]針對電樞捕獲效應的數學模型做定量分析，在模型中通過改變驅動線圈參數來減小電樞的捕獲效應，使發射效果最優。文獻[15]通過在驅動線圈中放置檢測裝置來評估線圈強度，通過測試與評估改進驅動線圈的結構。文獻[16]設計了一種非對稱的驅動線圈模型，為每一級線圈單獨設計結構以獲取更好的結果。

由于趨膚效應的影響，感應電流在電樞中的分布是不均勻的，電流絲法將電樞分為若干電流環，當細分足夠小時可以假設每個環上的電流是均勻的,以此來精確細化模型[17]。運動過程中,電樞受到的電磁力與電樞和驅動線圈間的互感梯度成正比,在建立的模型中,互感梯度需要得知運動中不同位置各電流環與驅動線圈的互感[18]，可以通過有限元軟件的靜態模型中計算，也可以通過互感計算手冊來查表計算[19]。相關研究對基于電流絲法建立模型已經有了比較成熟的方法，但是對于過程中未觸發的驅動線圈，必然會受到之前觸發線圈的影響[20]。回路中功率開關器件的存在使放電過程非線性化。觸發與未觸發的驅動線圈要做分開處理，不僅增加了模型復雜程度，而且計算時容易出現錯誤，模型要求高。

本文將基于電流絲法建立動態過程的完整模型，用開關函數以及虛擬大電阻等效驅動線圈回路晶閘管以及二極管的工作狀態，整合已觸發和未觸發的驅動線圈模型，簡化電路的數學模型。研究線圈的最佳觸發策略，并利用MATLAB/Simulink建立線圈炮的路模型，電流絲與驅動線圈互感通過Ansys有限元仿真軟件計算獲得，將結果導入到Simulink模型中，減少路模型實時計算工作量，提升仿真速度，將結果與有限元仿真結果進行比較，并在實驗平臺進行實驗，驗證模型的正確性。

1 電流絲法原理

1.1 線圈炮模型

為了簡化線圈炮的分析，作如下假設：

1)線圈是理想圓且所有線圈同軸；

2)電樞是理想圓柱筒，各處電導率和密度相同；

3)電樞位于線圈中心位置，且與線圈同軸；

4)忽略線圈外部弱導磁材料的影響。

基于線圈炮的軸對稱性，采用電流絲(current filament method，CFM)以電阻、自感、互感、電感梯度、電壓等位參數，將三維問題簡化為二維問題，建立線圈炮的電磁路方程。

電流絲法模型如圖1所示，由于電樞電流沿軸向分布，若將電樞劃分為m個同心圓環，則當圓環截面足夠小時，可以認為感應電流在截面上均勻分布，即用m個“電流絲”來等效電樞感應電流。這樣，線圈炮路方程可以表示為變系數常微分方程。

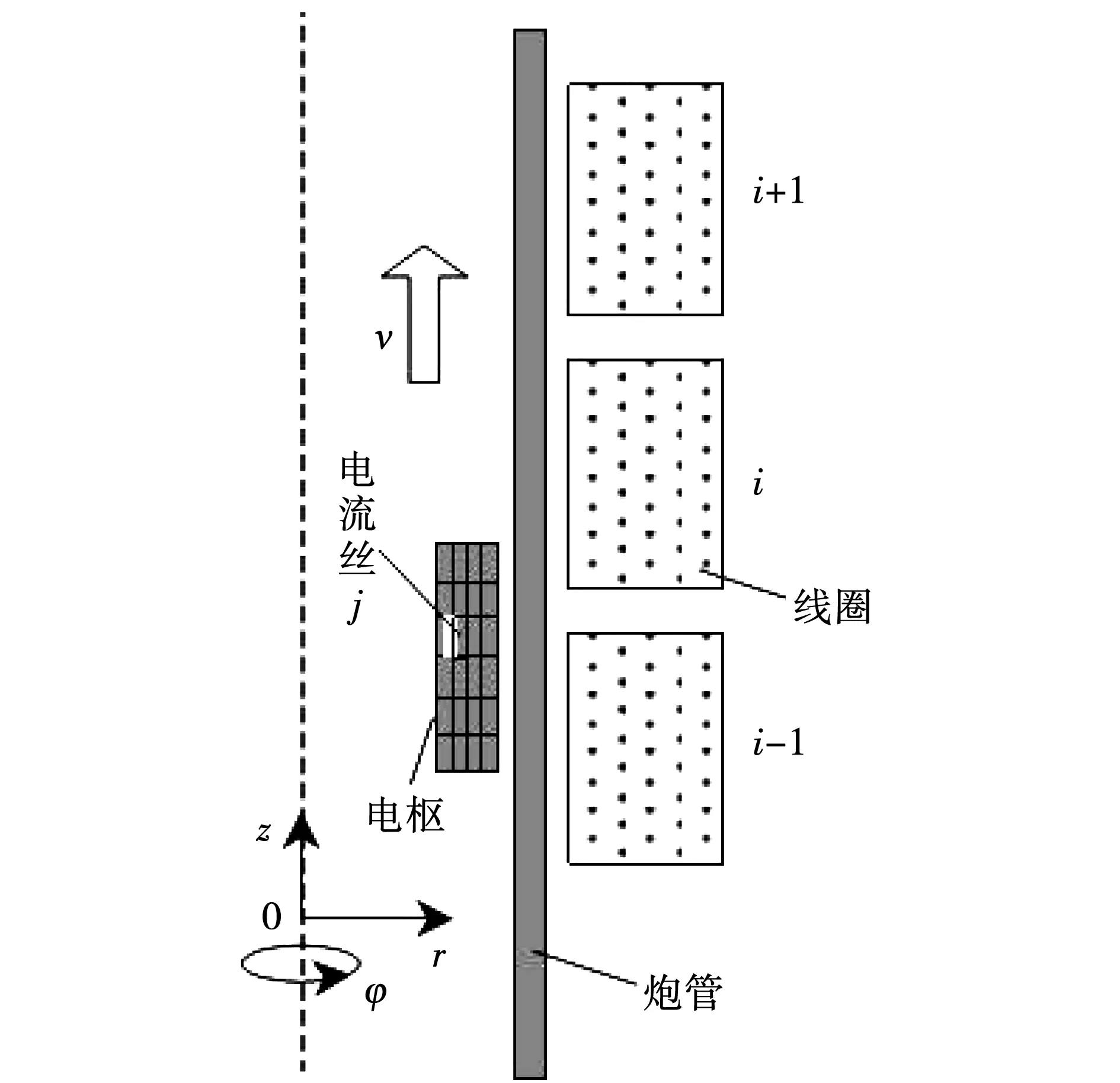
圖1 線圈炮電流絲法示意圖

線圈通常采用litz線繞成多匝結構，匝間彼此絕緣，可以忽略線圈導線渦流，因此，單個線圈中每匝激勵電流相等。假設激勵線圈有n級，根據基爾霍夫電壓定律，可以將電壓方程用矩陣形式表示為：

(1)

式中：Us表示線圈斷開電壓，是n維向量；φs表示線圈磁鏈，是n維向量；Rs表示線圈電阻，是n×n矩陣；Is是線圈電流，n維向量；φr是電樞環磁鏈，m維向量；Rr是電樞環電阻，m×m矩陣；Ir是電樞環電流，m維向量。

磁鏈方程為：

(2)

式中：Ls是線圈電感矩陣，n×n矩陣；M是線圈和電樞環互感矩陣，n×m矩陣；Lr是線圈電感矩陣，m×m矩陣。

電樞受到的電磁推力方程為

(3)

式中dM/dz表示沿電樞發射方向——軸向的互感梯度矩陣，是n×m維矩陣。

運動方程為：

(4)

式中：m是發射體質量；v是電樞速度；z是電樞位置。

1.2 電容驅動型電流絲法

電容通過高功率充電機恒流充電模式[21]，連接晶閘管、二極管以及負載組成脈沖形成網絡[22]。電容驅動型線圈炮電路如圖2所示，當晶閘管觸發時，電容向線圈釋放電壓，當電容電壓釋放至0，線圈電流再通過二極管支路續流，二極管支路串聯電阻可以減小續流時間，降低晶閘管和二極管損耗。

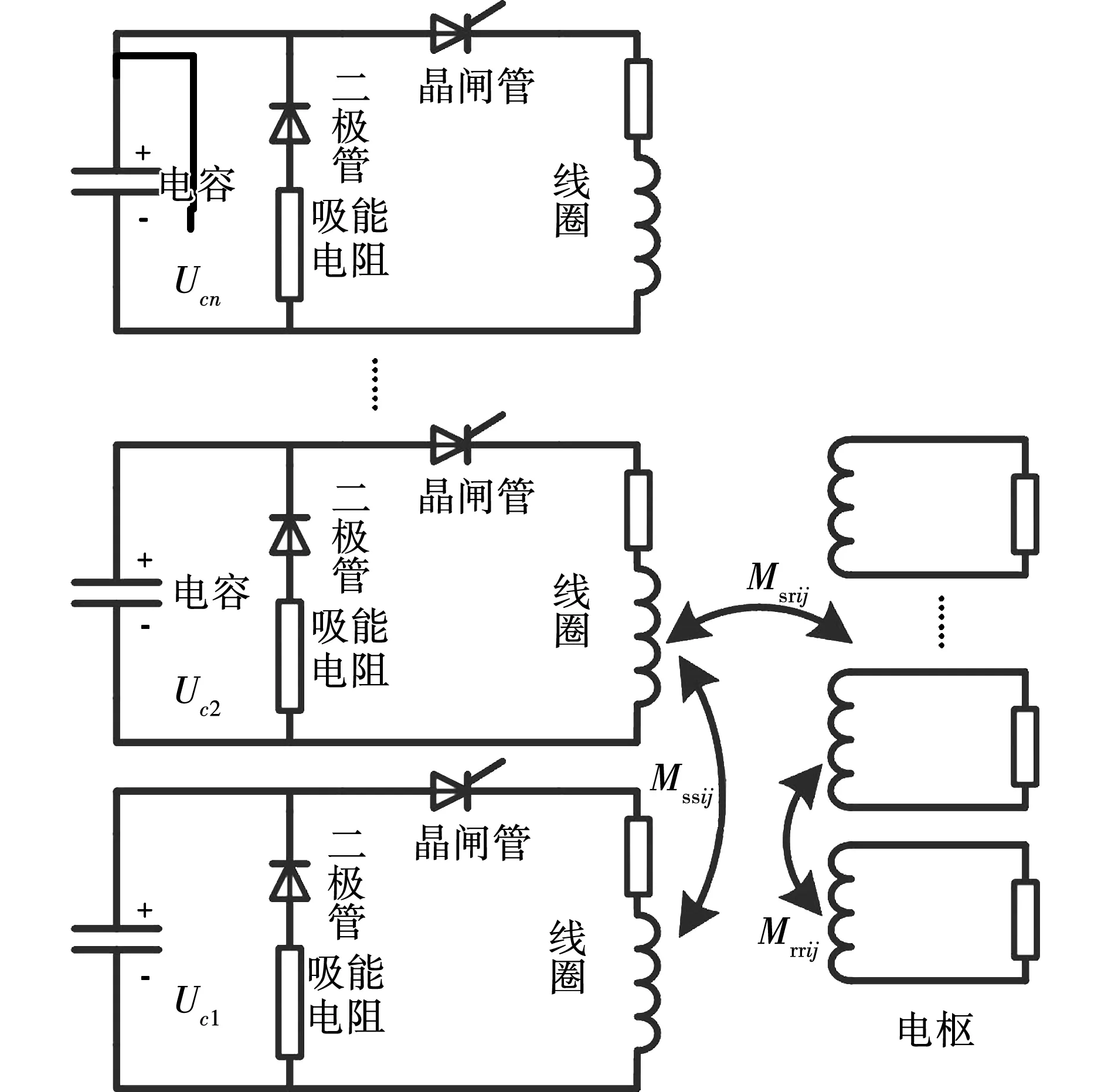
圖2 電容驅動型線圈炮電路圖

由于晶閘管和二極管的存在，造成供電回路的非線性，使得電流絲法建立的線圈回路方程復雜，分晶閘管觸發前和觸發后兩種情況。

根據式(1)和式(2)，晶閘管觸發前第i級線圈的回路方程為：

(5)

式中：usi和isi是第i級線圈電壓和電流；Mi1，Mi2,…,Mim是互感矩陣第i行。

晶閘管觸發后，第i級線圈的回路方程為

(6)

式中rs是線圈電阻。

電樞電流方程為

(7)

晶閘管觸發后，電容放電分兩個階段，第一階段通過電容向線圈放電，如圖3所示。

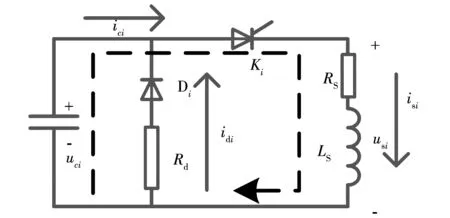
圖3 電容放電電路圖

電容放電回路方程為：

(8)

式中：C是電容值；uci和ici是第i級電容電壓和電流；idi是二極管支路電流。

當電容電壓降為0后，電容放電轉入第二階段二級管續流階段，如圖4所示。

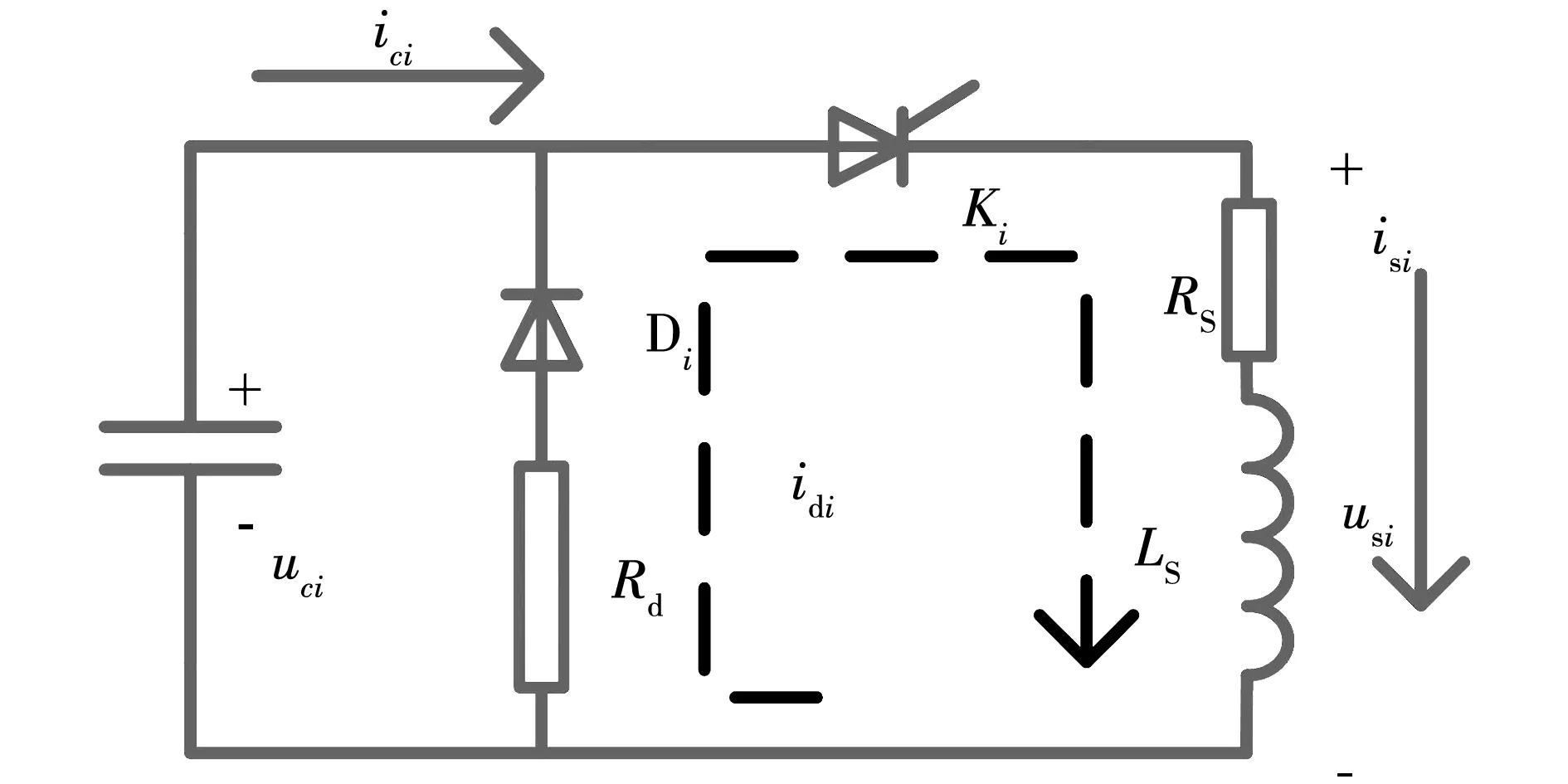
圖4 二極管續流電路圖

續流回路方程為：

(9)

式中rd是二極管支路電阻。

一般來說，多級線圈炮是按順序逐級觸發供電的，設第1～k級線圈已觸發供電，第k+1～n級線圈未供電，匯總前面的分析，此時線圈炮回路方程用矩陣形式表示為：

(10)

(11)

式中：v是電樞運動速度；下標1_k表示向量或矩陣取對應元素1,2,3,…,k；下標k+1_n表示向量或矩陣取對應元素k+1,k+2,…,n，例如Mk+1_n是(n-k)×m矩陣，形式為

2 改進型電流絲法

2.1 等效電阻法

原有電流絲法應用在電容驅動型線圈炮時，由于半控器件引入非線性，增加了分析困難。由式(9)所描述的回路方程可知，需要根據觸發情況，對n級線圈進行分段處理，已觸發的k級線圈和未觸發的n-k級線圈要采用不同的微分方程組。

為了解決這種情況，在線圈回路引入虛擬大電阻，如圖5所示。若晶閘管未觸發，則線圈支路串入大電阻；觸發后，大電阻變為0。

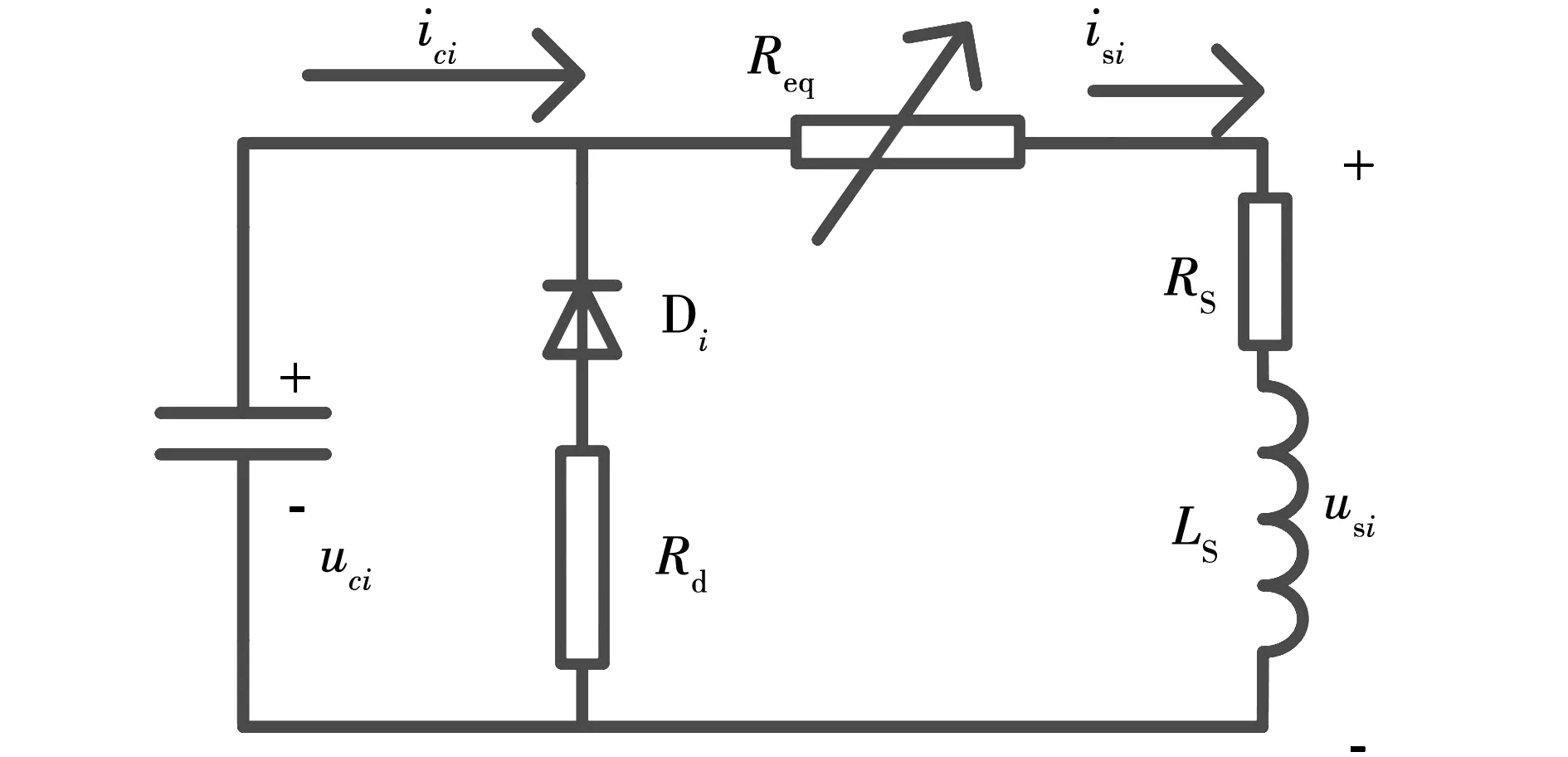
圖5 等效電阻放電電路

加入虛擬大電阻后，式(10)可以寫為

(12)

式中Req1_k是k×k對角矩陣，元素是req。當req足夠大時，Is近似相等為0，式(12)和式(11)具有相同形式，因此，將觸發與未觸發狀態線圈回路方程整合列寫為

(reqS+Rs)Is。

(13)

式中：req是虛擬大電阻，根據正常工況，電容儲存電壓值為6 000 V，若要使虛擬大電阻等效關斷時的晶閘管，需要考慮使其留過電流與該工況下的漏電流近似相等，已知晶閘管的漏電流一般小于10 mA，那么根據計算，虛擬大電阻的阻值可以是1 MΩ；S是開關對角矩陣，S=diag[0,0,…,0,1,1,…,1]，前k個對角元素是0，后n-k個對角元素是1，表示前k級線圈觸發，而后n-k級線圈未觸發。這樣，結合電樞方程，整個線圈炮改進電流絲法回路方程可以寫為

(14)

引入虛擬大電阻后，線圈炮路方程不必采用分段微分方程組形式，可采用統一形式，大大簡化分析計算。

相應地，電容放電回路也可以處理更簡單，不需要考慮本級是否觸發導通，直接采用式(8)和式(9)計算電容電壓，當回路存在大電阻時，計算出的放電電流近似為0，可以等效認為本級未觸發。

2.2 系數分析

分析式(13)，由于各線圈之間相對位置不變，電樞電流絲之間相對位置也不變，因此，Ls、Lr是定常矩陣，Rs、Rr也是定常矩陣。而M、dM/dz是變系數矩陣，是線圈和電樞之間相對距離的函數，電流絲與線圈的互感關系如圖6所示。

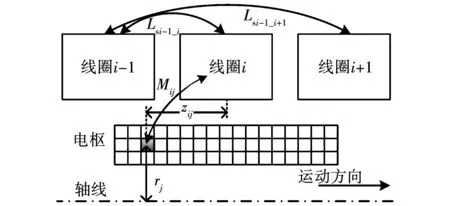
圖6 電流絲自感互感矩陣示意圖

由于M、dM/dz矩陣是隨電樞位置z變化的系數，使得式(14)是變系數微分方程，對其求解比較費時。對式(14)進行變換，令：

傳統農業植保工作的開展，以大型機械、人工操作為主導，前者具有作業效率高的特點，但卻存在設備成本高的缺陷；后者呈現耗時長、人力資源多的問題［2］。而在無人機技術的衍生下，植保無人機的使用改變了傳統植保模式，使植保工作更具快速性、高效性。植保無人機的優點具體如下。

(15)

則式(13)可以寫為

(16)

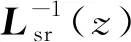
2.3 觸發控制

電容驅動的線圈在晶閘管觸發后，由于線圈時間常數較大，電流上升存在一定時間，當電樞速度較高時，上升時間內電樞會運動較長距離，而線圈和電樞耦合出力范圍較短，因此，需要考慮電流上升時間和電樞運動速度。

該觸發方式是在電樞運動至耦合出力點較大位置前，提前觸發線圈，當線圈電流達到最大時，電樞恰好運動到耦合出力點，使電樞推力達到最大。

觸發方式示意圖如圖7所示，觸發時刻電樞位置是z，第i級線圈和電樞最佳耦合位置是Zsi，電樞速度是v，線圈電流上升時間是Tr。則第i級線圈觸發在滿足下式關系時，可獲得較優觸發效果，有

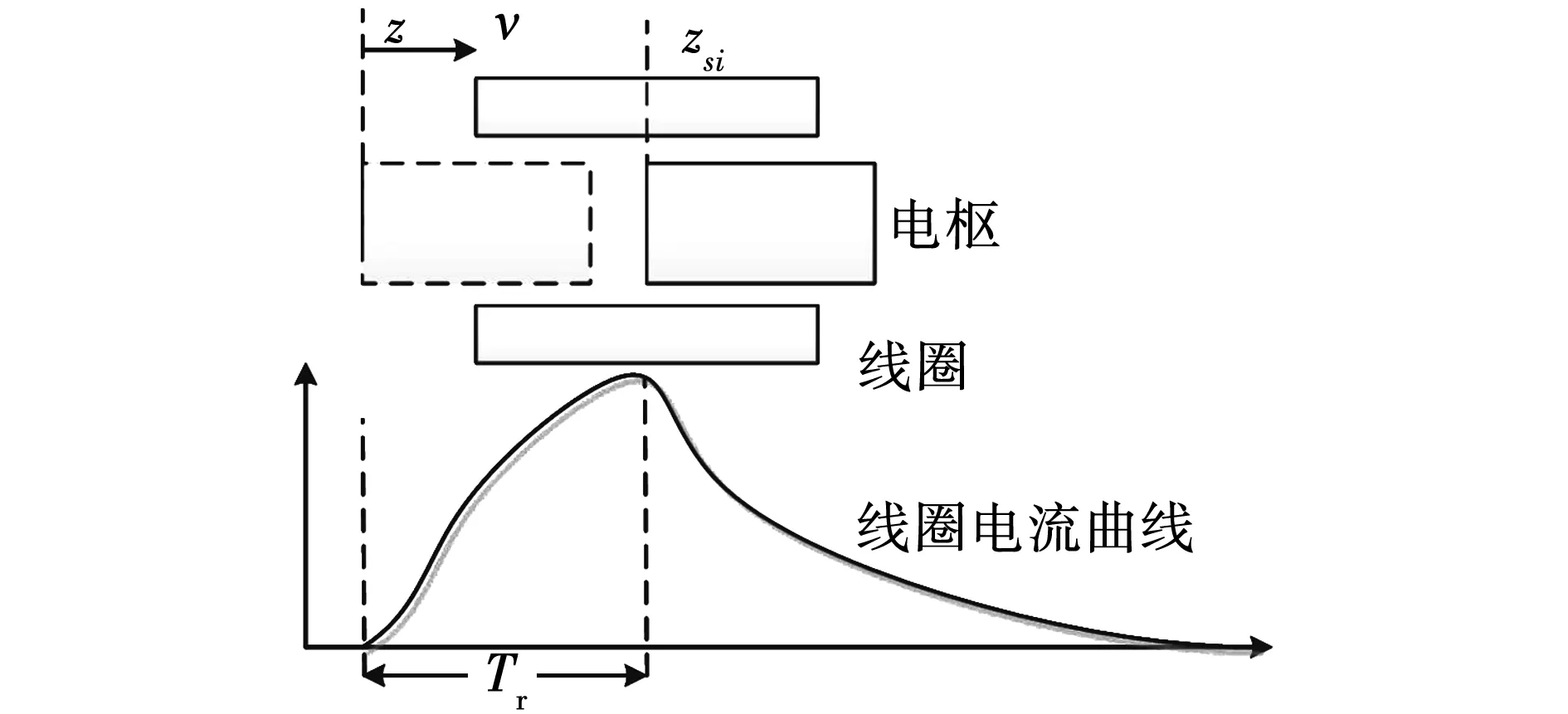
圖7 觸發方式示意圖

(17)

式中Si是第i級線圈的晶閘管觸發信號。在模型中，當某級線圈滿足式(17)的觸發條件，S矩陣中相對應的一位由1變為0，即從大電阻變成0。

3 仿真分析

采用前面分析方法，在MATLAB/Simulink中搭建電容驅動型多級感應線圈炮仿真程序，模型框圖如圖8所示。模型將脈沖回路中的晶閘管等效替換為大電阻Req，使用SFUNCITON模塊建立其數學模型，計算出電樞運動的電磁推力，使用Simulink中的積分函數得到電樞的速度與位移量，經過觸發策略單元，輸出虛擬電阻的S矩陣，構成了完整的系統仿真模型。

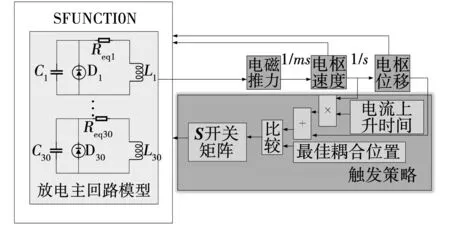
圖8 線圈炮仿真模型

線圈炮系統的參數如表1所示。

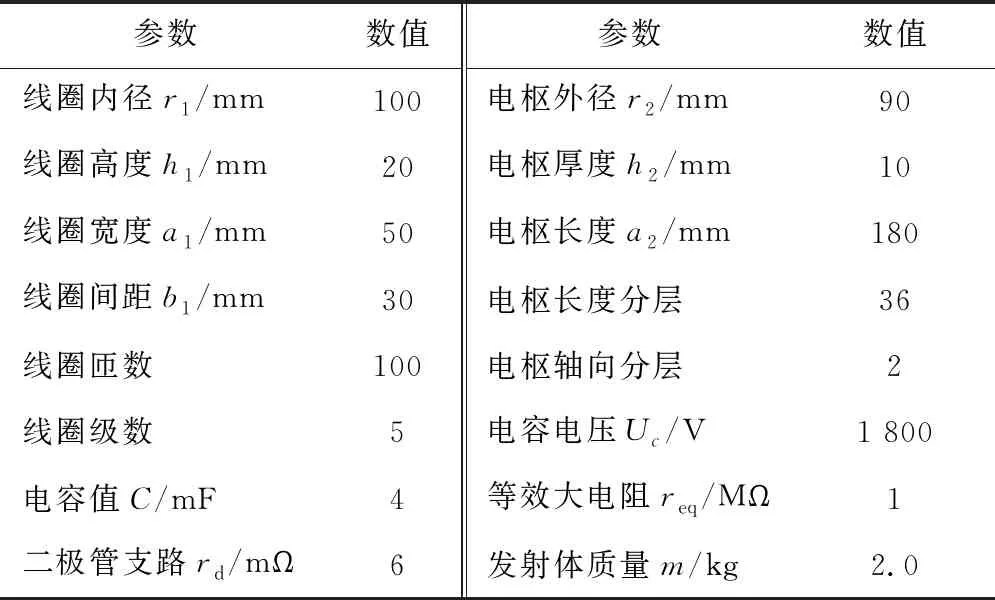
表1 線圈炮系統參數

采用有限元法提取電流絲法仿真所需的靜態參數，按表1參數，n=5、m=72,Ls是5×5矩陣，采用Ansys計算線圈自感和線圈之間互感，線圈自感為220 μH，相鄰線圈之間互感為75 μH，隔1個線圈之間互感為31 μH，隔2個線圈之間互感為15 μH，隔3個線圈之間互感為8.9 μH。

同理，Lr是72×72矩陣，由于參數較多，這里不再寫出，電流環軸向互感曲線如圖9所示。

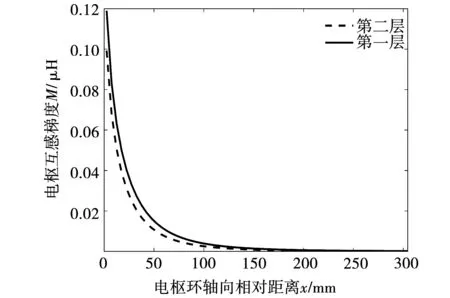
圖9 電樞互感曲線

計算單個電流環與單個線圈之間的互感和互感梯度曲線如圖10所示，其中，將線圈徑向從外到內劃分為4層計算。

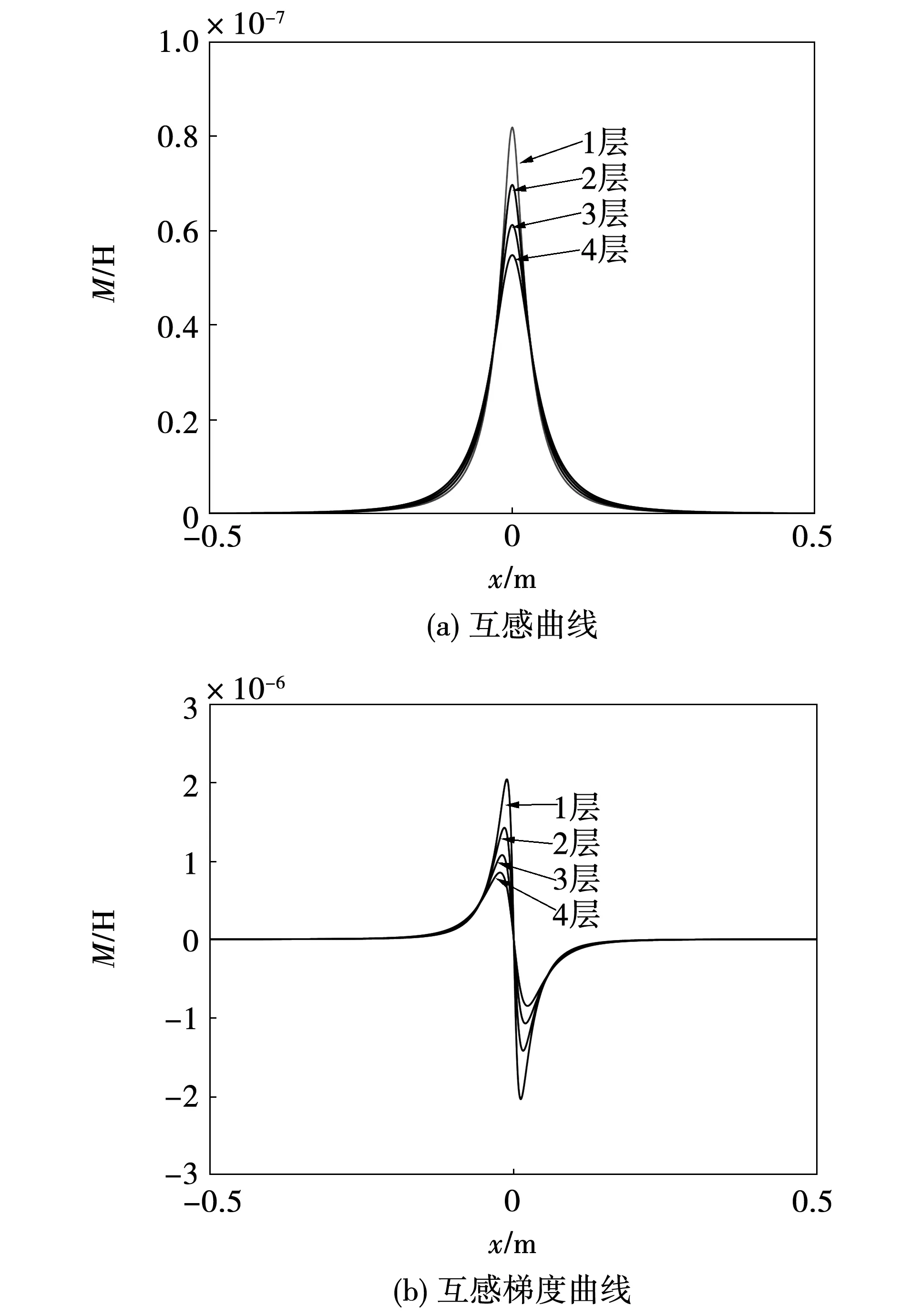
圖10 電樞電流環與線圈的互感與互感梯度曲線

當電樞電流環和線圈之間軸向距離超過200 mm后，互感和互感梯度可以忽略不計。

5級線圈總長度是400 mm，線圈長度80 mm，單個線圈耦合范圍在(-300,300)mm，因此線圈和電樞的互感和互感梯度矩陣只需考慮相對距離值(-380,430)mm時對應的互感及互感梯度值，將有限元中的互感結果導入到MATLAB數學模型中，直接利用矩陣進行計算，大幅減少了計算量，提升了計算速度。對整個發射過程進行仿真，并在MAXWELL有限元仿真軟件中建立同樣的場路耦合模型進行比較。采用式(15)改進電流絲法進行計算，觸發控制策略采用式(16)，根據現有裝置的轉換效率，預期出口速度在70 m/s。最終得到的仿真結果如圖11和圖12所示。

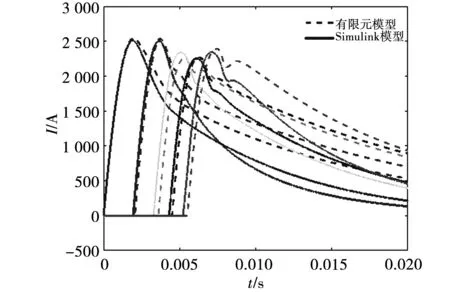
圖11 各級線圈電流曲線

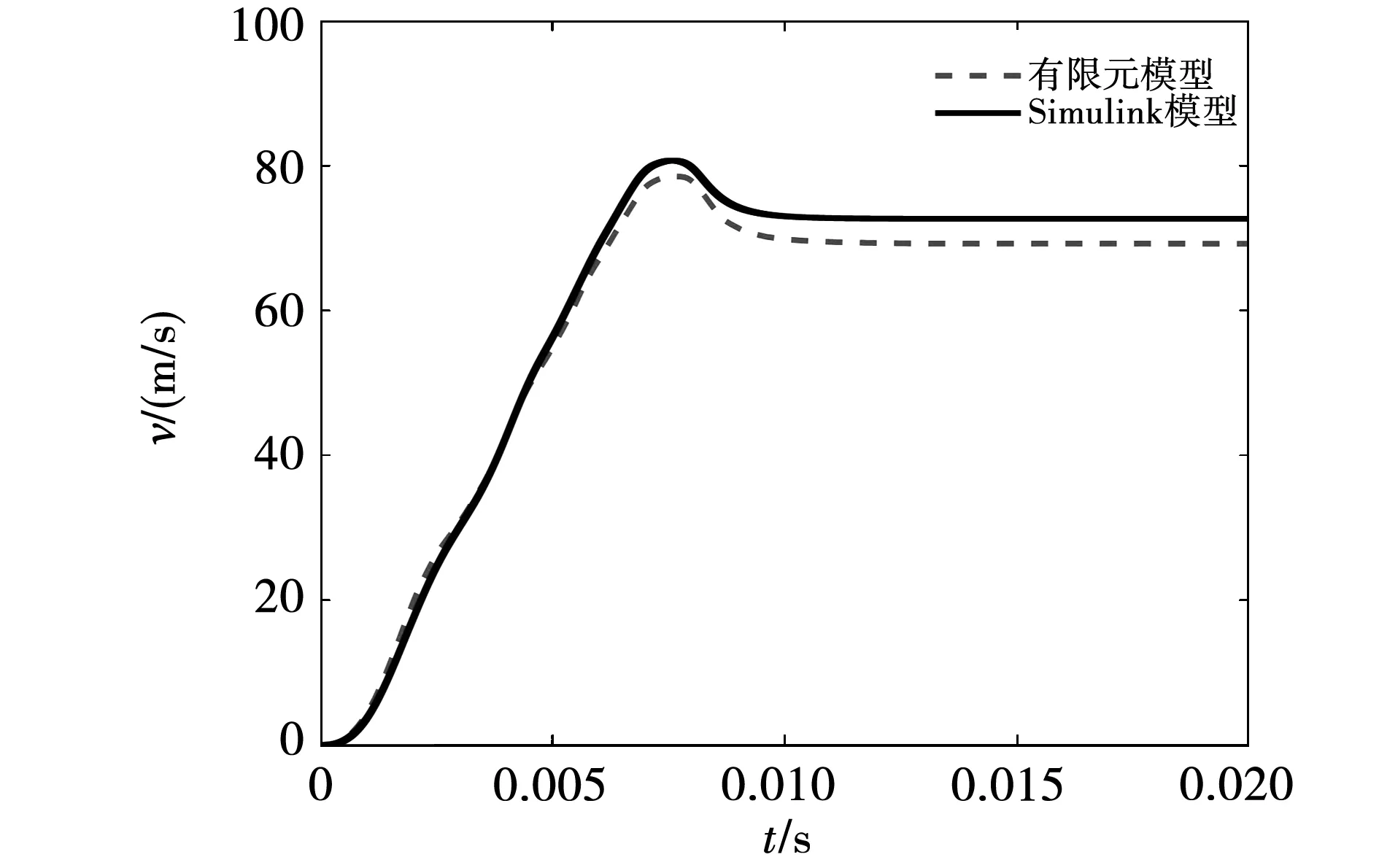
圖12 電樞速度曲線

對有限元仿真模型與Simulink模型進行比較，設置相同的目標時間，Simulink模型比有限元模型仿真速度快50%。且通過仿真可以看出，脈沖回路放電過程按照逐級放電的順序正常放電，有限元模型與Simulink模型的各級放電曲線的上升沿吻合度高，3、4、5級觸發時刻有細微差別，說明兩個模型中的電樞運動不是完全一致的，從圖12中也可以看出，兩個模型的速度曲線存在3%的誤差，經分析，由于在Simulink中的電樞環以及線圈參數都是固定的，其中電樞的電阻不能像有限元精細剖分，趨膚效應考慮得并不充分，所以電流曲線在下降階段會出現較大誤差。最終仿真的出口速度達到了71 m/s，仿真結果達到了預期分析的速度。

4 實 驗

通過圖13所示的五級線圈發射裝置實驗平臺對仿真模型進行驗證。

圖13 五級線圈發射裝置實驗平臺

在額定電壓下的各級放電電流曲線如圖14所示，并與有限元放電結果進行比較。可以看出，實際放電曲線與仿真相比，上升沿出現較大誤差，經分析是由于模型中的線圈參數是根據有限元中仿真計算得到，與實際線圈存在偏差，下降沿吻合度相較于兩個模型之間的吻合度較好。這說明有限元模型中的模型具有更好的參考意義，Simulink模型中存在誤差。

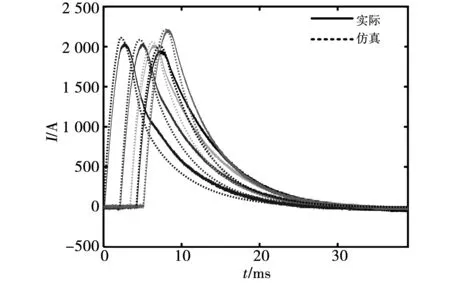
圖14 實驗平臺五級電流放電曲線

采用光電傳感器在出口測算速度，最終的速度為65 m/s，與仿真結果相差7%，存在一定誤差，是由于電流曲線決定了電樞運動受力，相對于仿真模型，實際電樞受力較小。

5 結 論

通過對多級感應線圈炮的電路方程以及運動方程進行分析，對模型進行了簡化，并在Simulink中搭建模型驗證簡化方法，結合實驗進行比較，得到以下結論：

1)探討了電容驅動型多級感應線圈炮的電流絲模型。引入等效大電阻使其合并為一個方程組，簡化了模型，優化了模型計算中的非線性過程，使其利于分析和仿真計算。同時將模型中互感矩陣部分做成查表形式，避免了整體計算求逆出錯的問題。與有限元計算方法相比提升了計算速度。

2)將Simulink模型與有限元模型進行比較。其中，放電電流的吻合度不高，經分析原因為兩種模型剖分方法不一致，導致電流曲線出現誤差，但是在連續脈沖形成的電樞受力曲線中，主要的影響因素是電流上升沿，所以兩個模型的運動曲線存在較小誤差。

3)通過五級線圈發射實驗平臺驗證了模型的正確性，結果存在一定誤差，但該模型對于電樞的運動分析具有一定的參考性，為之后系統提高性能、尋找最優觸發策略提供了新的模型參考。