一種磁鏈重構的雙三相PMSM分布參數建模方法

鐘再敏， 任舉， 尹星

(同濟大學 汽車學院，上海 201804)

0 引 言

近幾年來，具有效率高、轉矩密度大且脈動低等優點的多相電機在各個領域受到了廣泛的關注[1-2]。雙三相永磁同步電機(permanent magnet synchronous motor，PMSM)是一種非對稱六相電機，其不僅具有多相電機的眾多優勢，同時兼具PMSM穩定可靠、調速范圍寬等優點，因此被大量應用到低壓大功率驅動場合，其中最具代表的就是電動車輛和混合動力車輛的電驅動系統[3-5]。

然而，雙三相PMSM在實際運行過程中受氣隙磁場非正弦、磁飽和等非線性因素的影響，尤其是兩套三相繞組之間的耦合互感不能被忽略，導致反電動勢中含有空間諧波，進而引起相電流中含有較高的5、7次電流諧波[6]。這些電流諧波會增大系統的損耗，影響雙三相PMSM的實際性能，因此需要針對雙三相PMSM的諧波分析及抑制問題進行重點研究。傳統的PMSM數學模型是基于集中式參數建立的，這種建模方法需要眾多假設前提，與電機實際運行狀態存在較大差異，難以反映出真實電機運行過程中的非線性特性和諧波特性，也無法實現對電機的準確控制。

為實現對電機空間諧波特性的準確描述，Zhong Zaimin等學者提出了“分布參數建模”方法，通過基于磁共能重構的數值解析方法來重建有限元分析(finite element analysis, FEA)的仿真結果，獲得了三相PMSM的分布參數數學模型，根據仿真和實驗證明了所獲得的數學模型可以準確地描述電機的磁飽和情況和空間諧波特性[7-8]。分布參數建模方法的本質是將磁場非正弦和飽和引起的空間變化特性用統一的數學模型加以解析化描述[9]。本文將分布參數建模思想推廣應用到雙三相PMSM的建模中。

首先，本文利用有限元數值分析法分析雙三相PMSM的空間諧波特性并獲得磁鏈的數值解，根據磁鏈的周期性特性，利用傅里葉級數展開及多項式擬合，獲得能準確描述磁鏈變化的數值解析模型。結合虛位移原理，得到雙三相PMSM分布參數模型中的轉矩模型及電壓方程，并將分布參數建模結果與FEA仿真結果進行對比驗證。最后，搭建基于分布參數模型的雙三相PMSM矢量控制仿真系統，復現雙三相PMSM在實際控制中的電流諧波特性。

1 傳統集中式參數的數學模型

雙三相PMSM的結構如圖1所示，其定子由兩套在空間位置上互差30°電角度的三相繞組(ABC繞組、XYZ繞組)組成，繞組均使用星型連接，并采用隔離中性點的方式[10]。

由于實際電機運行過程較為復雜，在建立集中參數數學模型之前，需要對雙三相PMSM做出如下假設前提：轉子永磁體產生正弦分布的磁場；忽略定子齒槽對磁場分布的影響；不考慮永磁體的磁飽和；穩態運行時繞組中的感應電動勢為正弦波，同時忽略空間諧波對磁場的影響[11]。

基于上述假設，建立電機的集中參數數學模型。對雙三相PMSM而言，傳統基于集中式參數的建模方法可以分為基于雙dq變換方法和基于矢量空間解耦方法(vector space decomposition,VSD)[12-14]。基于雙dq變換的建模方法是利用傳統三相電機建模中的雙反應理論，對兩套三相繞組分別進行坐標變換，最終得到兩個三相之間存在耦合的數學模型[15]，其坐標關系如圖2所示。其中d1q1、d2q2軸在空間位置上重合，d1q1軸為ABC繞組對應的同步旋轉坐標系，d2q2為XYZ繞組對應的同步旋轉坐標系。

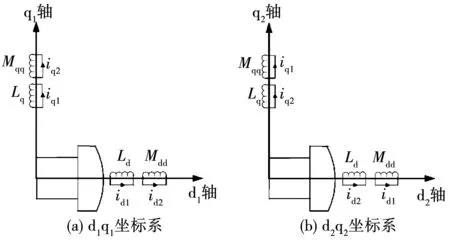
圖2 雙dq變換的坐標系

基于VSD的建模思路則是通過將電機的各變量分別映射到與機電能量轉換有關的D1Q1子空間和與機電能量轉換無關的D2Q2子空間中，最終獲得解耦形式的數學模型[16]。圖3為VSD變換的坐標系，其中，D1軸與永磁體軸線保持一致，Q1軸空間上超前D1軸90°，電機各變量的基波和12n±1次諧波被映射到D1Q1子空間中。D2Q2軸為諧波子空間，電機各變量的6n±1次諧波被映射到D2Q2子空間中。

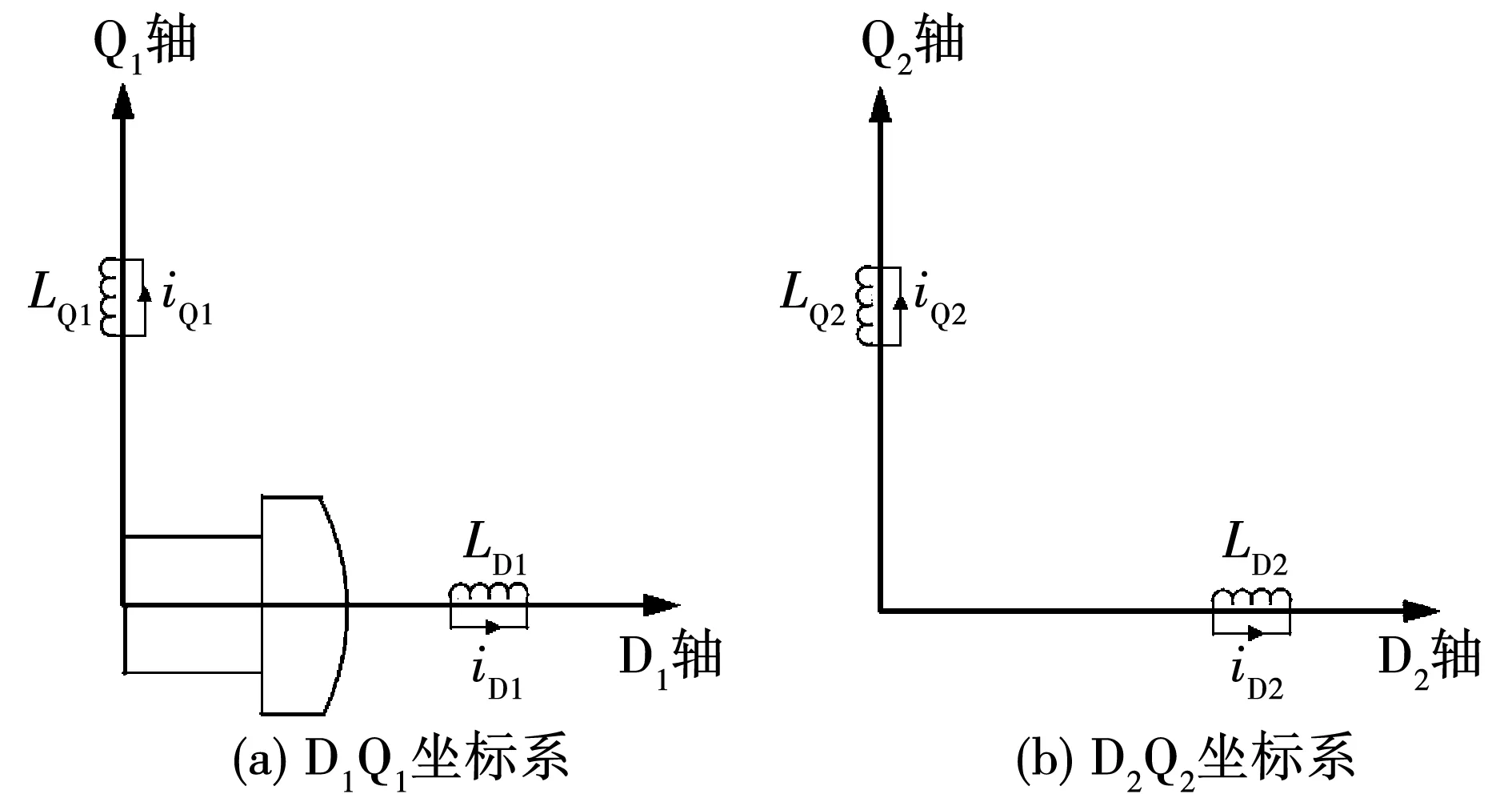
圖3 VSD變換的坐標系

基于雙dq變換和基于VSD的建模方法本質上只是坐標變換方法的不同，使得最終控制的電流分量不同，在實際應用過程中可以針對不同的需求進行選擇。由于雙dq變換坐標系的物理意義相較于VSD變換方法更加明確。因此在后續建模分析過程中通過坐標變換將靜止坐標系下的電磁參數變換到圖2的雙dq同步坐標系下，從而可以更加明顯看出電磁參數的空間諧波分布情況。而基于VSD的建模方法相較于雙dq變換方法解耦更加完全，且VSD控制結構可以對D2Q2軸的諧波電流進行獨立控制，其靈活度優于采用雙dq變換的矢量控制，因此，后續在控制方案上統一采用基于VSD的矢量控制結構。

然而，上述的雙三相PMSM集中參數建模方法都是在眾多假設前提下建立的，在雙三相PMSM的實際應用場景中為提高功率密度，電機鐵心一般工作在磁飽和狀態，電機氣隙磁場難以保證完全正弦分布。由于這些非理想因素的影響，隨著轉子位置的變化，電機的實際參數中必定包含空間諧波，因此以集中式參數建立的雙三相PMSM的數學模型無法準確描述電機實際運行過程中的空間諧波及飽和特性。

2 基于磁鏈重構的分布參數模型

為了能夠對電機實際運行過程中的磁飽和情況和空間諧波特性進行準確描述，考慮通過分布參數建模的方法建立電機的數學模型。首先通過FEA仿真獲取磁鏈的數值解，在此基礎上獲得磁鏈的解析模型并得到基于分布參數的電壓方程和電磁轉矩模型。

2.1 FEA模型建立及數值解獲取

FEA仿真可以真實的模擬實際電機的磁飽和、齒槽影響、以及各相繞組之間的耦合情況，獲得電機各個電磁參數隨轉子位置變化的分布波形。為了分析雙三相PMSM真實的空間諧波特性和非線性因素對電機的影響，采用某款車用雙三相PMSM為研究對象并建立如圖4的FEA仿真模型，其參數如表1所示。

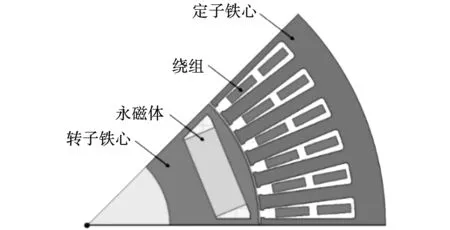
圖4 雙三相PMSM的二維FEA模型(1/8)

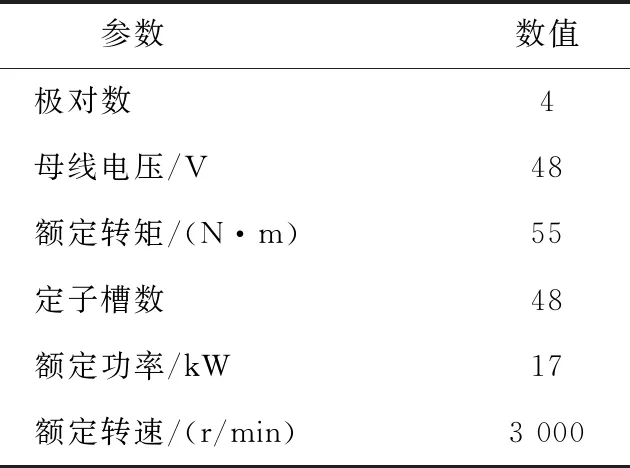
表1 雙三相PMSM有限元模型主要參數

考慮到實際的雙三相PMSM由于定子結構、磁飽和、漏磁所引起的非線性特性影響因素，磁鏈的變化往往比較復雜，綜合分析實際的影響因素，可以將磁鏈表示成

ψs=f(Is1,β1,Is2,β2,θr)。

(1)

式中：Is1為ABC三相電流幅值；β1為ABC三相定子電流矢量與d軸的夾角，即轉矩角；Is2為XYZ三相電流幅值；β2為XYZ三相定子電流矢量與d軸的夾角；θr為轉子位置角(見圖1)。當勵磁電流采用正弦電流激勵時，相應的工作點由(Is1,β1,Is2,β2)確定。

由圖2的雙dq變換坐標系可知，d1q1對應第一套ABC三相繞組，d2q2對應第二套XYZ三相繞組，通過將六相靜止坐標系下的電磁參數變換到雙dq同步坐標系下來觀察電磁參數的空間諧波分布情況。圖5和圖6顯示了Is1=Is2=108 A,β1=β2=120°工況下仿真得到的雙三相PMSM的磁鏈和轉矩FEA結果。圖中ψd1、ψq1為ABC三相磁鏈在轉子dq軸坐標的投影，ψd2，ψq2為XYZ三相磁鏈在轉子dq軸坐標的投影。

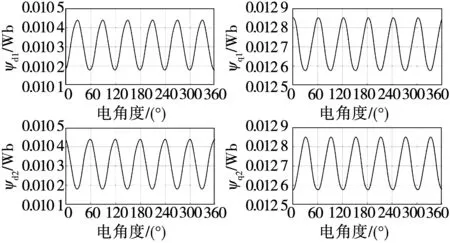
圖5 工況點(108 A,120°,108 A,120°)仿真的磁鏈數值解

圖6 工況點(108 A,120°,108 A,120°)仿真轉矩

從圖5的仿真結果可以看出，磁鏈隨著轉子位置呈周期性分布，其周期為π/3。圖6雙三相PMSM的電磁轉矩存在12、24次轉矩脈動，但整體的轉矩脈動幅值不大，最大僅為0.3 N·m，這也說明了雙三相PMSM較傳統三相PMSM的一個顯著的優勢就是其轉矩脈動小。

根據磁鏈與工況點的關系，為方便后續的建模，將磁鏈表達式的參考系由極坐標形式轉化為直角坐標形式，則最終磁鏈的表達式為

ψs=f(Is1,β1,Is2,β2,θr)=

f(id1,iq1,id2,iq2,θr)。

(2)

式中：id1、iq1為ABC三相定子電流矢量在轉子dq軸上的投影；id2、iq2為XYZ三相定子電流矢量在轉子dq軸上的投影，自變量的對應關系為：

(3)

2.2 磁鏈解析模型

根據磁鏈在轉子位置θr上的周期性，對所有工況點的磁鏈數據進行一維傅里葉級數展開。對于雙三相PMSM系統而言，其能量主要集中在基頻附近，因此傅里葉級數的階次可以縮小到有限的階次。以ψd1為例，展開的表達式為

(4)

式中：ak、bk為傅里葉級數的階數k所對應的系數；N為傅里葉展開的最高階次。

式(4)描述了磁鏈與轉子位置的關系，但對于不同工況點，由于電流不同，磁鏈ψd1的值也會發生變化，為了獲得磁鏈隨電流大小的變化情況，采用將傅里葉系數描述成隨電流變化的函數的方法，如下所示：

(5)

式中：Ak,Bk(k=0,1,…,N)為1×15的行向量，可通過使用最小二乘法獲得。并且考慮到雙三相PMSM兩套三相繞組之間的耦合以及磁飽和情況，選擇電流基函數為

(6)

為了簡化整個磁鏈解析表達式，將各向量用矩陣的形式表示為：

(7)

最終，d1軸磁鏈隨轉子位置和電流變化的表達式為

(8)

同理，d2、q1、q2軸磁鏈也可通過上述方法進行處理：

(9)

式中：Ax、Bx(x=d1,q1,d2,q2)為根據FEA結果(Ak,Bk)計算得到的維度為(N+1)×15的系數矩陣。每個磁鏈表達式均由三部分組成，表達式充分考慮了磁鏈隨轉子位置以及電流大小的變化情況。

為了驗證所建立的磁鏈解析表達式的準確性，在相同工況點下對重構的磁鏈模型與FEA仿真所得結果進行對比。考慮到復雜性與精確性之間的平衡，在所構建的磁鏈重構模型中，傅里葉級數系數為6，即N=6。圖7、圖8顯示了在某兩個工況點下，磁鏈解析模型所得結果與FEA仿真結果的對比，為便于展示細節，鑒于磁鏈的周期性，在此采用六分之一電周期的磁鏈進行展示。從圖中可以看出，所建立的磁鏈解析模型可以很好的描述磁鏈隨轉子位置的變化情況，同時與FEA所得結果有高度的一致性，驗證了所建立的磁鏈解析模型的準確性。

圖7 磁鏈解析模型與FEA結果對比(27 A,100°,27 A,100°)

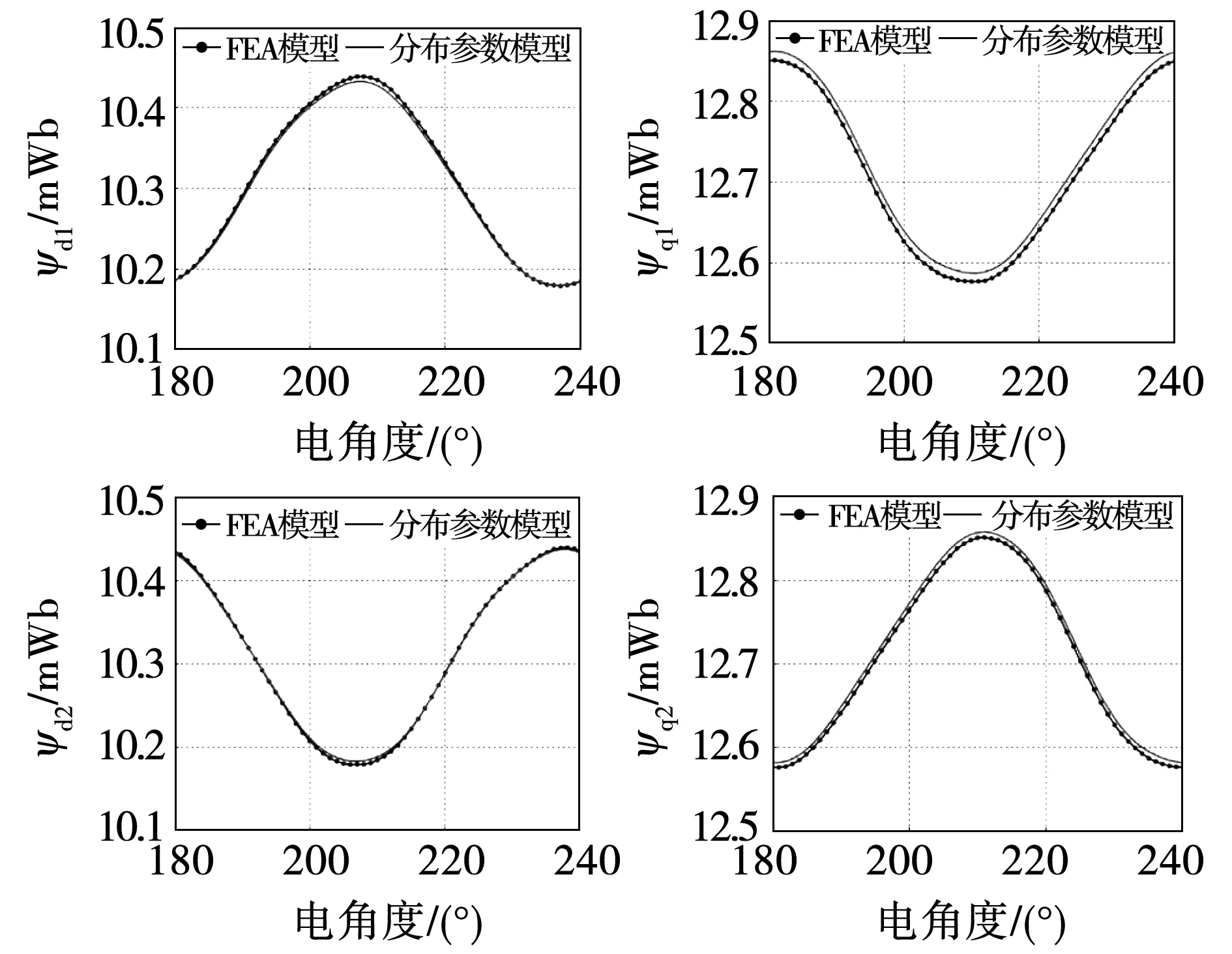
圖8 磁鏈解析模型與FEA結果對比(108 A,120°,108 A,120°)

2.3 電壓方程

根據磁鏈解析模型，可以推導出雙三相PMSM的電壓方程。在雙dq坐標變換下，雙三相PMSM的電壓方程如下：

(10)

式中：ud1、uq1為ABC三相定子電壓矢量在轉子dq軸上的投影；ud2、uq2為XYZ三相定子電壓矢量在轉子dq軸上的投影；Rs為定子電阻；ωr為轉子電角速度。該方程為雙三相PMSM電壓方程的一般表達形式，根據之前所建立的磁鏈解析模型，將磁鏈解析模代入電壓方程，就能得到能描述空間諧波特性的電壓解析方程，為簡化表達，令

P=diag(0,1,…,k,…,N1,0,1,…,k,…,N1)。

則有電壓方程為：

(11)

由式(11)可知，磁鏈直接體現在電壓方程中，從而磁鏈諧波可以間接影響電流諧波。因此下文在仿真和實驗的過程中通過電流諧波來直觀地表現分布參數模型對電機諧波特性的準確描述以及諧波前饋抑制算法的有效性。

2.4 電磁轉矩模型

為了得到電磁轉矩的解析模型，需從能量傳遞角度出發，電磁轉矩Te可以由磁共能對轉子位置角求偏導獲得

(12)

式中pn為極對數。磁共能Wc(id1,iq1,id2,iq2,θr)可以通過磁鏈對電流積分得到，即

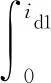
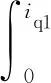
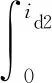
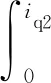
(13)

令id1=d1iq1,id2=d2iq1,iq2=q2iq1，選擇合適的積分路徑，可得磁共能的解析表達式為

(14)

式中

根據虛位移原理，磁共能Wc(id1,iq1,id2,iq2,θr)對轉子位置θr的偏導即為轉矩，即

(15)

根據式(3)，取id1,iq1,id2,iq2關于轉子位置θr的偏導：

(16)

將式(16)代入式(14)，可得電磁轉矩的解析模型為

(17)

式(17)為最終的電磁轉矩解析模型，該模型描述了轉矩隨不同電流，不同轉子位置的變化情況。轉矩公式由五部分組成，第一部分為磁共能對轉子位置求偏導所產生的轉矩脈動，主要包括齒槽轉矩等，后四部分則為傳統意義上磁鏈與電流作用生成的平均轉矩，但因為此時磁鏈為重構的解析模型，故平均轉矩也考慮了實際電機的空間諧波變化情況。

圖9展示了不同工況點下建立的轉矩解析模型與FEA模型的對比結果，可以看出轉矩的解析模型可以很好的描述轉矩隨轉子位置的空間諧波情況。

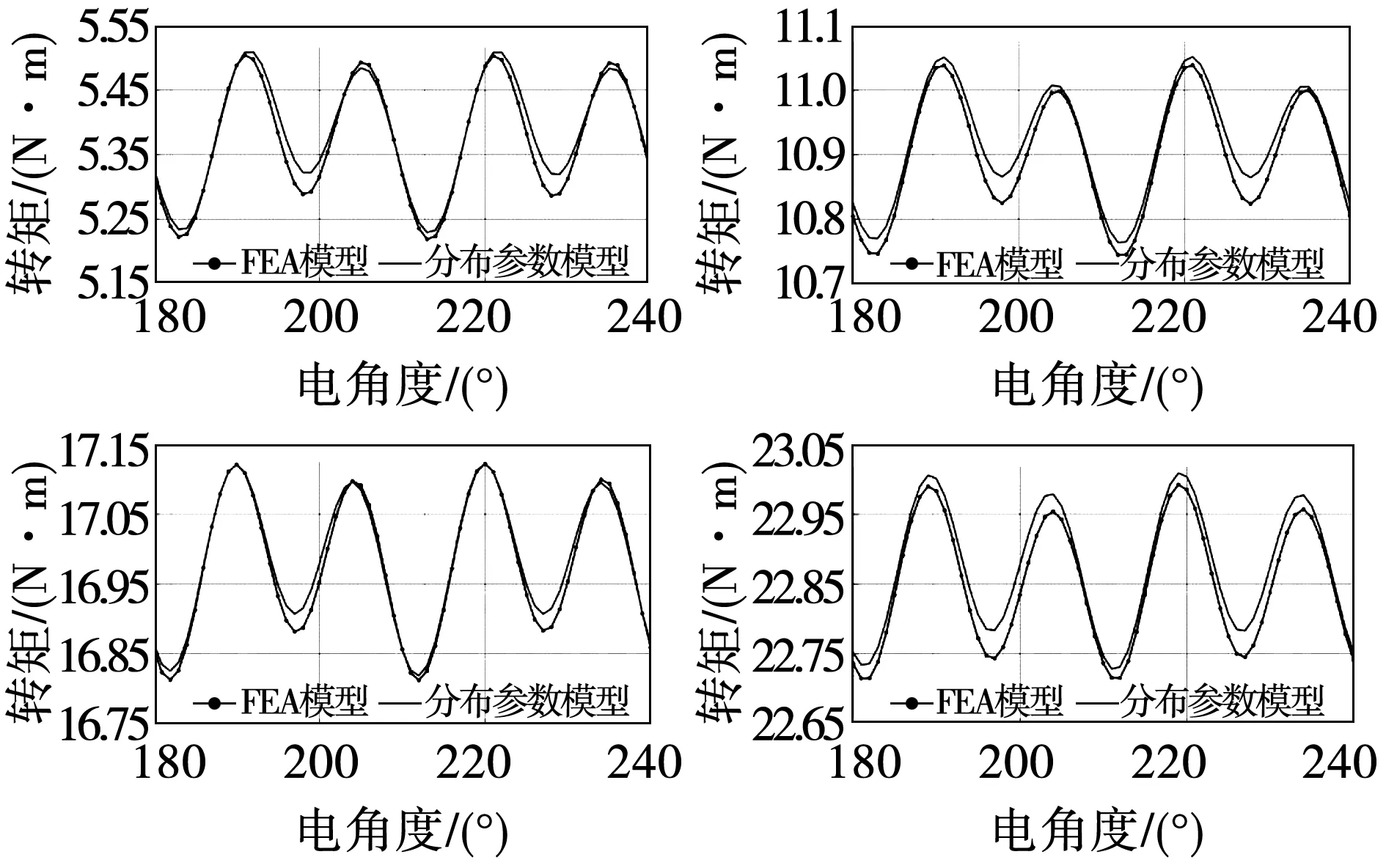
圖9 電磁轉矩解析模型與FEA結果對比

式(8)的磁鏈方程，式(11)的電壓方程和式(17)的轉矩方程表征了雙三相PMSM的空間分布諧波特性，構成完整的分布參數模型，至此，實現了將三相PMSM分布參數建模思想拓展應用于雙三相PMSM的建模。

3 仿真及實驗分析

為了將上述不同建模方法的實現效果進行對比分析，建立了雙三相PMSM的離線仿真系統。圖10顯示了VSD框架下的矢量控制框圖，通過VSD變換將電機電磁參數變換到參與機電能量轉換的D1Q1空間和不參與機電能量轉換的D2Q2空間。控制系統采用4個電流環分別控制D1Q1、D2Q2軸電流，由于D2Q2軸電流主要為諧波電流，因此在實際控制中將D2Q2軸的電流設定值設為0。

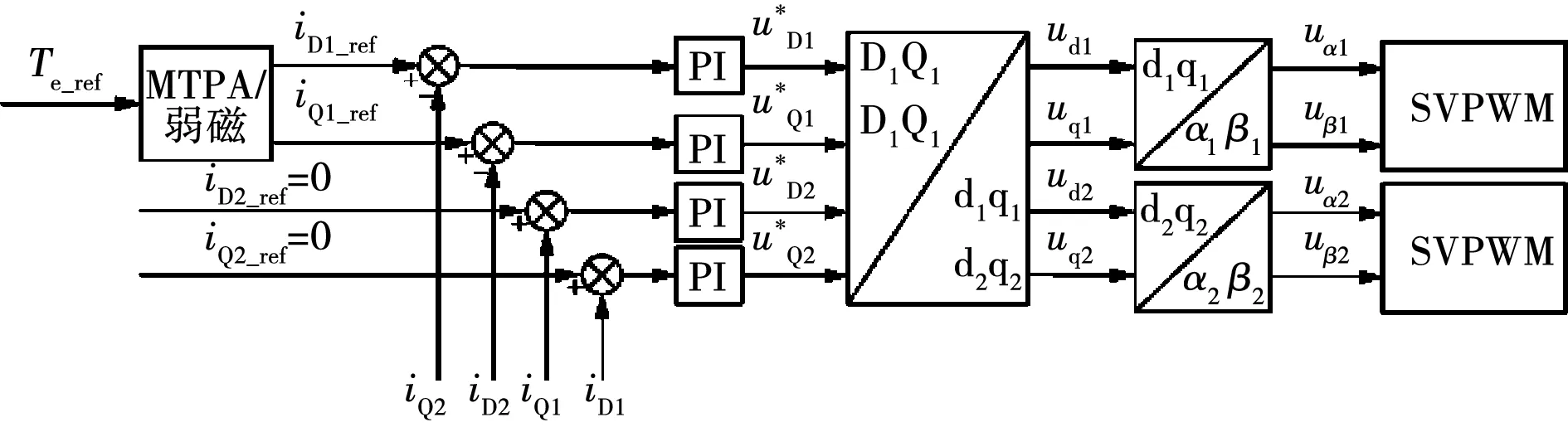
圖10 基于VSD的雙三相PMSM矢量控制框圖

同時，為了調制的方便，采用兩個獨立的三相SVPWM調制器來實現雙三相PMSM的調制，因此，需要將VSD形式下的電壓矢量變換到雙dq形式下，變換矩陣為

(18)

采用圖10的控制框架在MATLAB/Simulink中建立整個控制系統的離線仿真程序，仿真模型使用如表1所示的電機參數。設置電機母線電壓為48 V，FOC中電流環PI參數為：kp=0.03;ki=20;仿真基準步長為1e-7 s。下文中仿真和實驗工況均為：電機轉速為1 000 r·min-1;轉矩為10 N·m。

3.1 基于集中參數數學模型的雙三相PMSM仿真

圖11為基于集中參數數學模型的仿真結果。從相電流波形可以看出，相電流波形的整體正弦度較好，基本無諧波電流，轉矩波形也較平穩，無明顯的轉矩脈動。正如第一節中所述，基于集中參數建立的數學模型難以準確描述電機實際運行過程中的空間諧波及飽和特性。

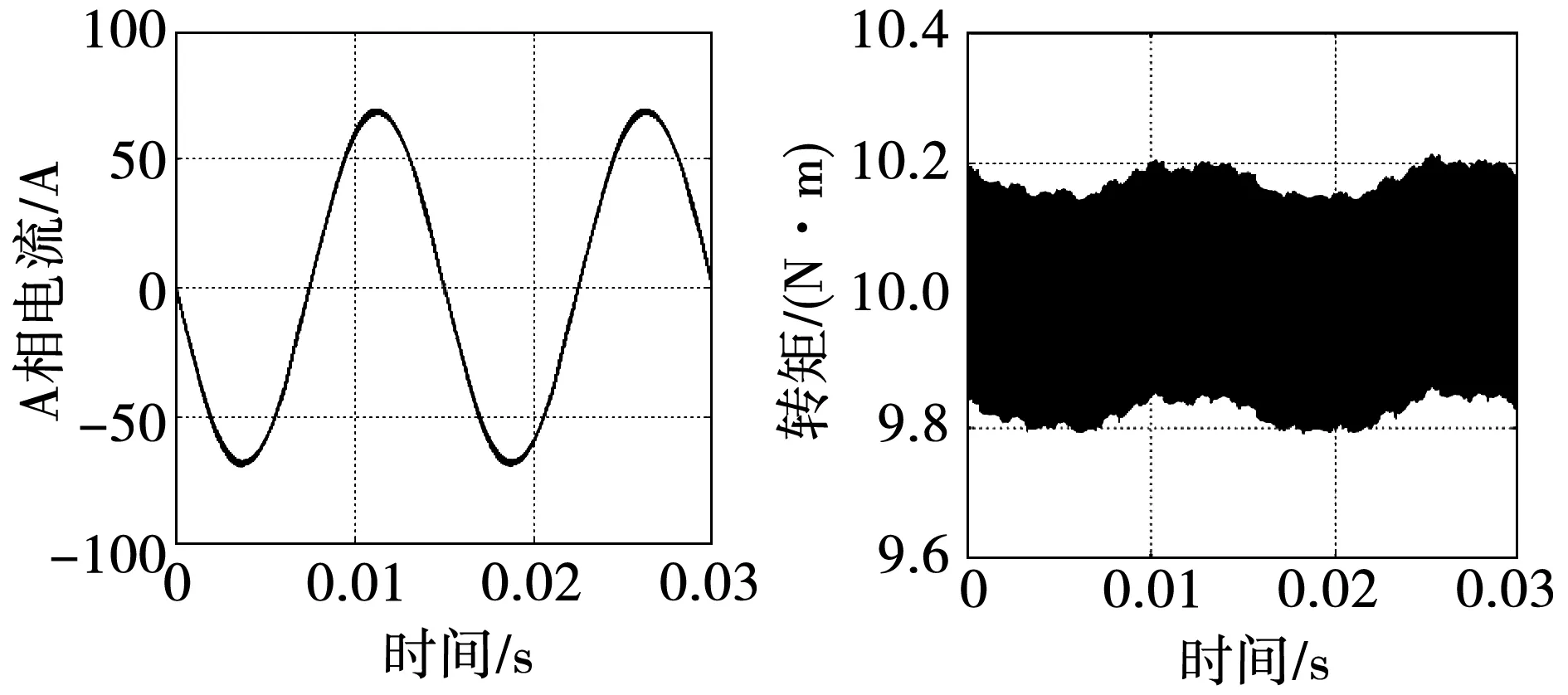
圖11 基于集中參數數學模型仿真的電流和轉矩波形

3.2 基于分布參數數學模型的雙三相PMSM仿真

圖12為基于分布參數數學模型的相電流仿真結果，對比圖11可以看出，采用雙三相PMSM的分布參數模型以后，相電流波形含有明顯的5、7次電流諧波，反映了實際電機的空間諧波特性。圖13為電磁轉矩波形及其FFT分析，從FFT分析可以看出，一個電周期內轉矩脈動以12、24次諧波為主，同時整體的轉矩脈動較小，因此在實際控制中可以忽略轉矩脈動的影響。

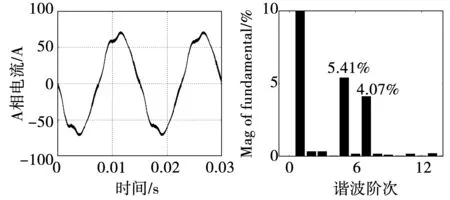
圖12 基于分布參數數學模型仿真的電流波形和FFT分析

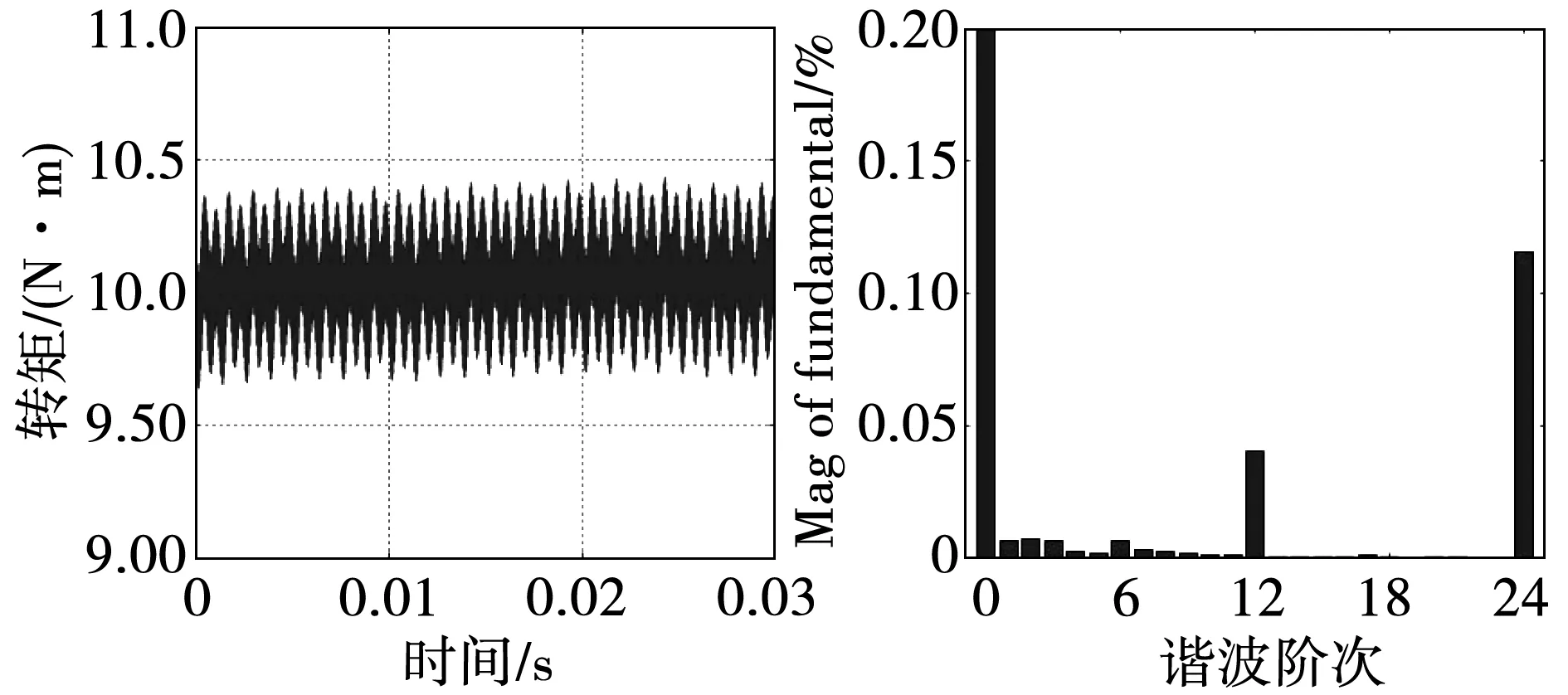
圖13 基于分布參數數學模型仿真的轉矩波形和FFT分析

3.3 實驗結果

圖14所示為雙三相PMSM實驗臺架。實驗電機參數與FEA模型一致(見表1)。逆變器以10 kHz的開關頻率工作，死區時間為5 μs。逆變器直流側電壓為48 V，控制信號采用基于TMS320F28335的DSP平臺產生，采樣頻率為10 kHz。此外，該控制方法不包括逆變器死區時間的補償算法。

圖14 雙三相PMSM實驗臺架

圖15是雙三相PMSM通過實驗得到的A相電流，可以看出電流波形與圖12中基于分布參數仿真獲得的A相電流波形較為一致，電流中都含有大量的5、7次諧波，證明了基于分布參數建立的數學模型能夠較為準確地描述電機實際運行過程中的諧波特性。由于仿真過程中未考慮逆變器死區的影響，使得仿真得到的電流中諧波含量比實驗所得諧波含量低。但總體而言，基于分布參數的數學模型對實際電機運行過程中的空間諧波特性的復現效果較好。

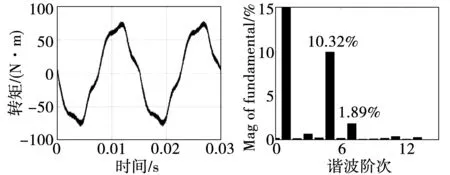
圖15 實驗所得A相電流和FFT分析

利用分布參數模型能準確描述電機的空間諧波特性的優勢，考慮通過前饋合適的諧波電壓的方法對電流諧波進行抑制。通過分布參數解析模型，可以準確計算需要前饋的諧波電壓。圖16為電機轉速1 000 r·min-1、轉矩10 N·m的工況下采用前饋諧波電壓抑制方法后的實驗結果，可以看出5次諧波含量由10.32%下降至2.08%，7次含量由1.89%下降至0.73%，抑制效果明顯。由于雙三相PMSM本身轉矩脈動相對較小，因此在不考慮對電機轉矩的影響下認為整體諧波抑制效果符合預期。通過諧波抑制的結果也進一步證明了分布參數數學模型對電機諧波特性描述的準確性。

圖16 基于前饋諧波電壓抑制方法的實驗結果

4 結 論

傳統基于集中參數的雙三相PMSM數學模型由于是在眾多假設條件下建立的，并不能準確反映真實電機的空間諧波特性，在離線仿真以及基于模型的控制算法開發上都有較大的局限性。因此，本文選擇利用分布參數的建模思想來建立雙三相PMSM的電機模型。

分布參數建模方法的本質是將磁場非正弦和飽和引起的空間變化特性用統一的數學模型加以解析化描述。本文通過重構磁鏈獲得了雙三相PMSM分布參數數學模型，將分布參數建模方法成功推廣應用到雙三相PMSM的建模中。通過將分布參數模型結果與FEA仿真結果進行對比，發現分布參數模型與FEA結果有著高度的一致性，可以準確反映雙三相PMSM的空間諧波特性。并通過仿真和實驗分析，證明了分布參數模型在表征雙三相PMSM空間諧波特性方面的有效性。