一種永磁電機齒槽轉矩測量方法

楊志堅， 張雨國， 喻桂華

(1.華南理工大學 機械與汽車工程學院，廣東 廣州 510640；2.廣州成揚科技有限公司，廣東 廣州 510640)

0 引 言

齒槽轉矩是在繞組不通電時，永磁體與電樞齒之間相互作用力的切向分量作用在電機轉子上所產生的波動轉矩[1]，其存在會引起轉矩脈動、轉速波動、電流諧波、振動噪聲等問題[2-6]。然而，在電機設計時，齒槽轉矩分析模型均建立在理想條件下，沒有考慮加工誤差等非理想條件。因此，即使設計時已使得齒槽轉矩達到性能要求，但實際中的非理想條件通常會使齒槽轉矩比設計時的大數倍且會引入其他頻率成分的齒槽轉矩，對電機控制性能造成不利影響。綜上，測量出電機齒槽轉矩諧波成分及其幅值大小對電機齒槽轉矩性能指標的評價、優化電機結構設計以及提升電機控制性能具有重要指導意義。國內外學者針對永磁電機齒槽轉矩的測量方法提出了多種方案，具體總結如下：從測量原理上主要分為三類：1)簡易測量法：電子秤法、砝碼法、杠桿測量法；2)扭矩傳感器測量法(直接測量法)：靜態傳感器、動態傳感器；3)電流電壓測量法(間接測量法)[7]。

簡易測量法主要是根據杠桿平衡原理來測量齒槽轉矩。文獻[8]提出杠桿測量法，測試時，用手拉動連接在力臂軸上的數字測力計，記錄力臂開始轉動瞬間力的大小值，再乘以力臂長度就可得到齒槽轉矩幅值。文獻[9]提出了砝碼法，在電機轉軸上裝支桿，砝碼通過輕質細繩懸掛在支桿的一端，定子上安裝刻度盤。測試時，轉動支桿到被測點的刻度，輕輕加掛砝碼，記錄支桿開始轉動時的砝碼質量，通過力矩平衡公式計算出齒槽轉矩。兩種方法都簡單易實現，但在齒槽轉矩大于摩擦轉矩時，轉子位置無法保持，無法測量。此外，兩者都忽視了摩擦轉矩的影響，拉力計精度、力臂長度、砝碼質量也影響著測試的誤差。所以上述兩種方法只適合齒槽轉矩比較大的電機，主要應用于定性測試分析中。為克服上面兩種方法的缺點，文獻[10]提出電子秤法，用可以精確控制轉動角度的裝置(如車床，步進電機)夾緊被測電機定子，在電機軸上加裝平衡桿，平衡桿兩端有支桿，通過調節電子秤高度使平衡桿保持水平，記錄電子秤示數并利用力矩平衡方程計算出齒槽轉矩。該方法原理簡單，但操作復雜，需要夾裝工具及多次重復測量，測試精度依賴于電子稱的靈敏度與夾裝定子裝置的步距角大小。

直接測量法通過轉矩傳感器來測量齒槽轉矩。文獻[11]提出步進電機靜態測試法，將被測電機、扭矩傳感器、步進電機緊固連接在同一軸線，控制步進電機旋轉一定角度后，利用步進電機自身的保持轉矩作為轉矩傳感器的一個固定端，可直接讀出作用在轉矩傳感器另一端的齒槽轉矩大小。文獻[12]提出動態測試法，通過控制器控制被測電機穩定轉動，電機通過聯軸器連接在傳感器一端，傳感器另一端也通過聯軸器與磁粉制動器相連，對傳感器采集的數據進行二次分析，得到齒槽轉矩。直接測量法原理與操作簡單，但都是需要高精度、價格昂貴的轉矩傳感，實驗系統的安裝要求較高。此外，靜態測量法需要配套高精度步進電機及驅動系統，動態測量法需要驅動器、磁粉制動器及配套電源系統且動態測量法忽視了驅動器及磁粉制動器引起的脈動轉矩。

間接測量法主要是通過檢測與齒槽轉矩有關的電壓、電流等參數，并從中提取出齒槽轉矩，文獻[13]提出測電壓法，該方法利用步進電機的矩角特性，通過檢測步進電機通直流電繞組上的感應電勢計算出被測電機的齒槽轉矩。該方法可在齒槽轉矩的一個周期內進行多采樣點測量，但方法復雜，操作繁瑣，步進電機感應電勢與力矩的曲線精度不高，測量誤差大。文獻[14]提出通過伺服驅動器驅動電機低速空轉，采集電機三相電流，提取出q軸電流，根據電機轉矩常數即可計算出齒槽轉矩。但是該方法忽視了驅動系統本身所引起的電流諧波，如逆變器非線性引起的q軸電流諧波。

綜上，目前永磁電機齒槽轉矩測量方法存在局限性、夾裝工具較多、操作繁瑣、需要配套高精度步進電機、轉矩傳感器等使得實驗成本高等問題。基于此，本文提出一種簡單的齒槽轉矩測量方法，直接利用電機自帶的編碼器、不需轉矩傳感器等額外器材，不需要搭建復雜的試驗臺、操作簡單、可行性高、成本低且測試精度也較高。此外，根據編碼器原理，其脈沖間隔在角域上是等角度間隔，而在時域上并非等時間間隔。本文實驗數據處理在角域進行，避免了角域轉換為時域時引起插值誤差。

1 齒槽轉矩特性

1.1 理想條件下的齒槽轉矩

當定轉子相對運動時，由于齒槽的存在，永磁體兩側面對應的一小段齒槽區域內磁導變化大，引起磁場儲能變化，從而產生齒槽轉矩，其表達式[1]為

(1)

式中：La為電樞鐵心有效長度；μ0是空氣磁導率；R1和R2分別為轉子軛外半徑和定子軛內半徑；Gn為有效氣隙磁導圓周分布函數；Br(nz/2p)為永磁體剩磁密度的平方沿圓周分布函數；z為定子槽數；n為使nz/2p為整數的整數；α為定轉子之間相對位置角。

齒槽轉矩以一個齒距為周期重復，只有當Gn和Brn諧波階次滿足nz/2p為整數時，才會產生齒槽轉矩，因此，齒槽轉矩的階次NL為槽數與極數的最小公倍數及其倍數，如下式所示，且階次越高，轉矩幅值越小，即

NL=LCM(z,2p)i。

(2)

式中：LCM表示極數與槽數最小公倍數；i為整數(i=1,2,3，…)；p為電機極對數。

從上述理論可知，從電機結構設計上減小齒槽轉矩可采取兩種方法：1)改變電機極槽配合來改變電機齒槽轉矩階次分布規律，使最小公倍數變大；2)改變電機定轉子結構減小Br(nz/2p)和Gn幅值，進而減小齒槽轉矩。

1.2 非理想條件下的齒槽轉矩

在電機加工制造、裝配過程中，定、轉子缺陷會產生附加的齒槽轉矩[15]。在電機設計階段主要通過有限元仿真在理想條件下優化電機結構來抑制齒槽轉矩，因此實際中非理想條件引起的齒槽轉矩得以凸顯且幅值可能大于理想條件下的齒槽轉矩。

1)定子缺陷產生的齒槽轉矩。

實際電機中存在定子鐵心偏心、橢圓、定子齒錯位、硅鋼片材料特性不一致以及嵌線過程中導致部分硅鋼片移位等缺陷會影響氣隙磁導的諧波成分，從而產生附加的齒槽轉矩諧波[16]。定子缺陷產生的典型的齒槽轉矩諧波次數(NAHCγi)為2p及其倍數次[17]，可表示為

NAHCγi=2pi(i=1,2,3，…)。

(3)

2)轉子缺陷產生的齒槽轉矩。

轉子缺陷主要是由于各永磁體的長度、寬度、厚度不一致，永磁體安裝位置與理想位置相錯位以及永磁體材料分布不均勻存在離散性等引起的。該缺陷會使得磁動勢分布不對稱、從而使永磁體磁動勢平方值諧波成分發生變化，產生附加的齒槽轉矩。轉子缺陷通常產生z及其倍數次的齒槽轉矩，可表示為

NAHCRi=zi(i=1,2,3，…)。

(4)

2 齒槽轉矩測試裝置

2.1 測試原理

圖1為所設計的齒槽轉矩測試系統示意圖，測試系統主要由圓盤、砝碼、電機及編碼器組成。測試時，選擇合適質量的砝碼使圓盤以盡可能較小的轉速轉動，進而帶動電機轉子同步轉動。

對整個測試系統進行動力平衡分析，在轉動過程中，施加在圓盤上的驅動力矩為

T=mgr。

(5)

式中：m為砝碼質量；g為重力加速度，取9.8 m/s2；r為圓盤半徑。

圓盤與電機轉子角速度相同，因此，電機轉動過程中，在電機轉子位置角θ處，動力平衡方程可表示為

(6)

式中：B為電機阻尼系數；J1為圓盤轉動慣量；J2為電機轉子的轉動慣量；Tcog為作用在電機轉子上的齒槽轉矩。

根據式(6)可得出齒槽轉矩表達式為

(7)

對于該測試系統，式(7)中砝碼質量m、圓盤半徑r、重力加速度g、電機轉動慣量J2、圓盤轉動慣量J1大小已知且恒定不變，其中J1可通過實際測試或通過軟件建模計算得出，電機轉子位置角θ可由編碼器采集得到，進而求得dθ/dt及d2θ/dt2。由于整個轉動過程中轉速相對較小，且電機本身的阻尼系數很小，因此可忽略電機阻尼系數B，即忽略式(7)中的阻尼力Bdθ/dt。至此，即可得到每個轉子位置處的齒槽轉矩。

由于在轉動過程中驅動轉矩大于齒槽轉矩與摩擦轉矩之和，所以電機是加速運動的。根據編碼器原理，其脈沖間隔在角域上是等角度間隔，而在時域上并非等時間間隔，因此，可在角域上利用階次濾波得到齒槽轉矩曲線和通過角域傅里葉變換得到齒槽轉矩所含諧波階次及幅值大小[18]。

2.2 測試系統

圖2為根據圖1所搭建的測試系統，其中圓盤半徑r=30 mm，轉動慣量J1為0.029 63 g·m2。在此，圓盤轉動慣量是通過軟件建模計算出其體積，測量加工后圓盤質量得到其密度，進而利用軟件計算而得。

圖2 測試系統

3 實驗結果分析

利用上述實驗方法對一臺8極12槽(2p=8，z=12)的表貼式永磁同步電機進行了實驗測試。電機參數如表1所示。

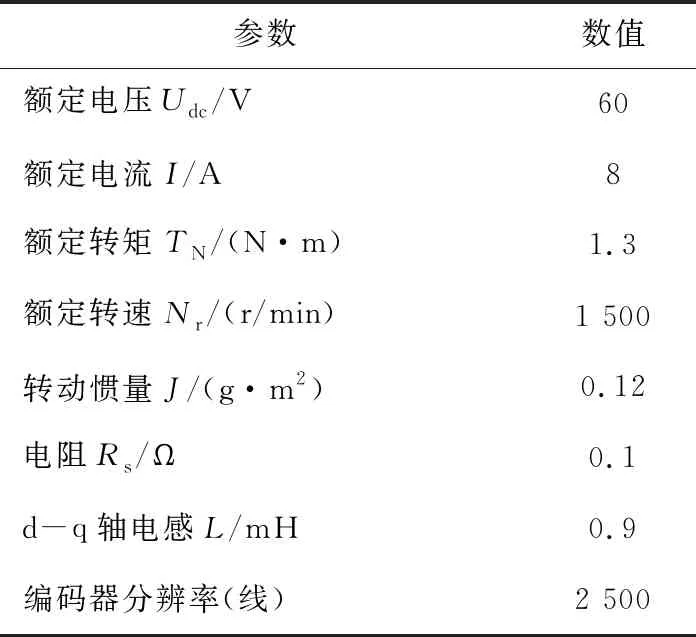
表1 電機參數

電機自帶的編碼器為增量式光電編碼器，分辨率為2 500線，電機轉動一圈輸出2 500個脈沖序列。此外，電機轉每一圈還會輸出一個脈沖序列Z，該脈沖對應電機的零位置，取點做角域傅里葉分析時，以該脈沖位置作為起始點，以保證每次取點時轉子初始位置角相同。

電機定轉子結構如圖3、圖4所示。電機定子采用開輔助齒方法來削弱齒槽轉矩[19]。整個定子在圓周方向上由不同材料硅鋼片制成的電樞齒與輔助齒相間拼接而成，因此容易導致定子不是一個理論上的圓而是橢圓。此外，拼接處的附加氣隙以及硅鋼片上的小孔等都是引起定子缺陷的主要原因。轉子缺陷主要是由于各永磁體之間參數差異以及永磁體在圓周上的安裝位置偏離理論位置。

圖3 電機定子

圖4 電機轉子

實驗所用砝碼質量m=62 g，將采集到的編碼器數據，以第一個電機零位置脈沖Z脈沖時刻作為轉子位置角起始零點與采樣時間零點，得到轉子位置角及其對應的脈沖時間點如圖5所示。

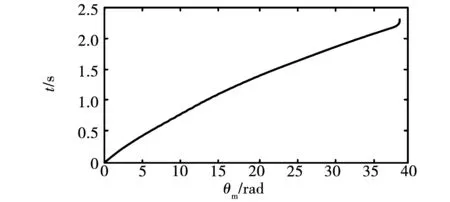
圖5 轉子位置角脈沖時間點

根據兩個角度脈沖之間的角度差及時間差，可得轉子角速度及角加速度如圖6、圖7所示。由于實驗所用電機齒槽轉矩比較小，為了減小測量誤差，電機轉速應盡可能小，因此砝碼質量也較小。剛開始放上砝碼時，輕輕撥動一下小圓盤使電機轉動，但砝碼質量小以及剛開始轉動時砝碼有輕微的擺動及轉動，因此從轉速圖中可以看出剛開始一小段時間內轉速波動偏大。

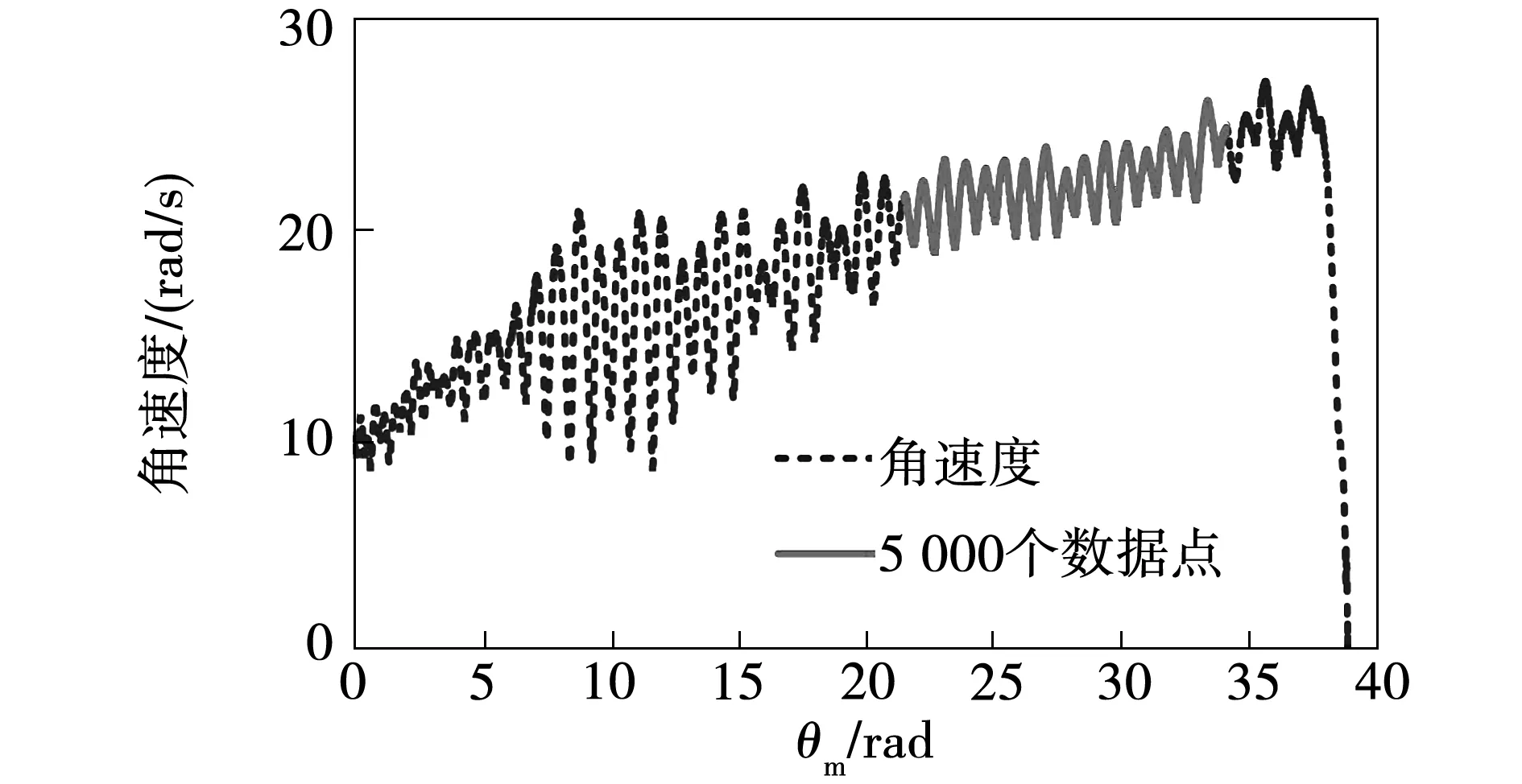
圖6 轉子角速度

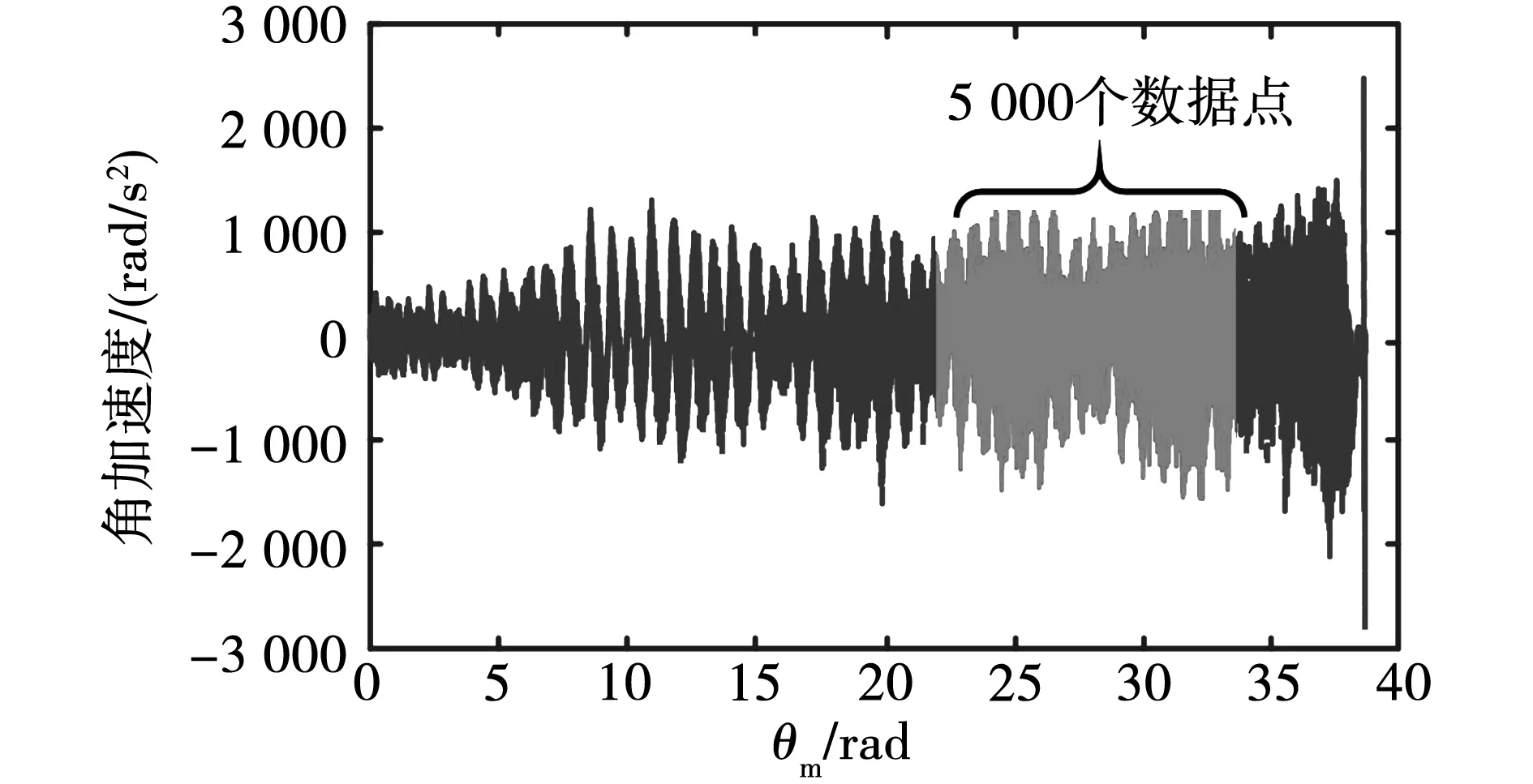
圖7 轉子角加速度

由此可由式(7)求出齒槽轉矩，由于轉速在剛開始時存在干擾因素使波動偏大，為減小測量誤差及后續的角域傅里葉變換，取圖6和圖7中砝碼下落過程穩定、轉速波動變化規律基本一致的兩轉數據(5 000個點)計算出的結果作為電機齒槽轉矩，得到的齒槽轉矩曲線如圖8所示。可以看出，齒槽轉矩含有高頻成分，結合圖7可知其原因主要是加速度是根據編碼器采集的脈沖角度差和時間差進行二階求導得到的，由于兩個脈沖時間間隔比較小，計算過程會引入高頻成分。

為去除高頻成分，得到齒槽轉矩曲線，對計算出的齒槽轉矩進行低通階次濾波，由理論可知齒槽轉矩階次越高幅值越小，根據電機參數，極數與槽數最小公倍數為24，為保留至少前48階齒槽轉矩，取濾波器截止階次為123階。濾波后取與圖8中相同數據點所對應的齒槽轉矩如圖9所示。

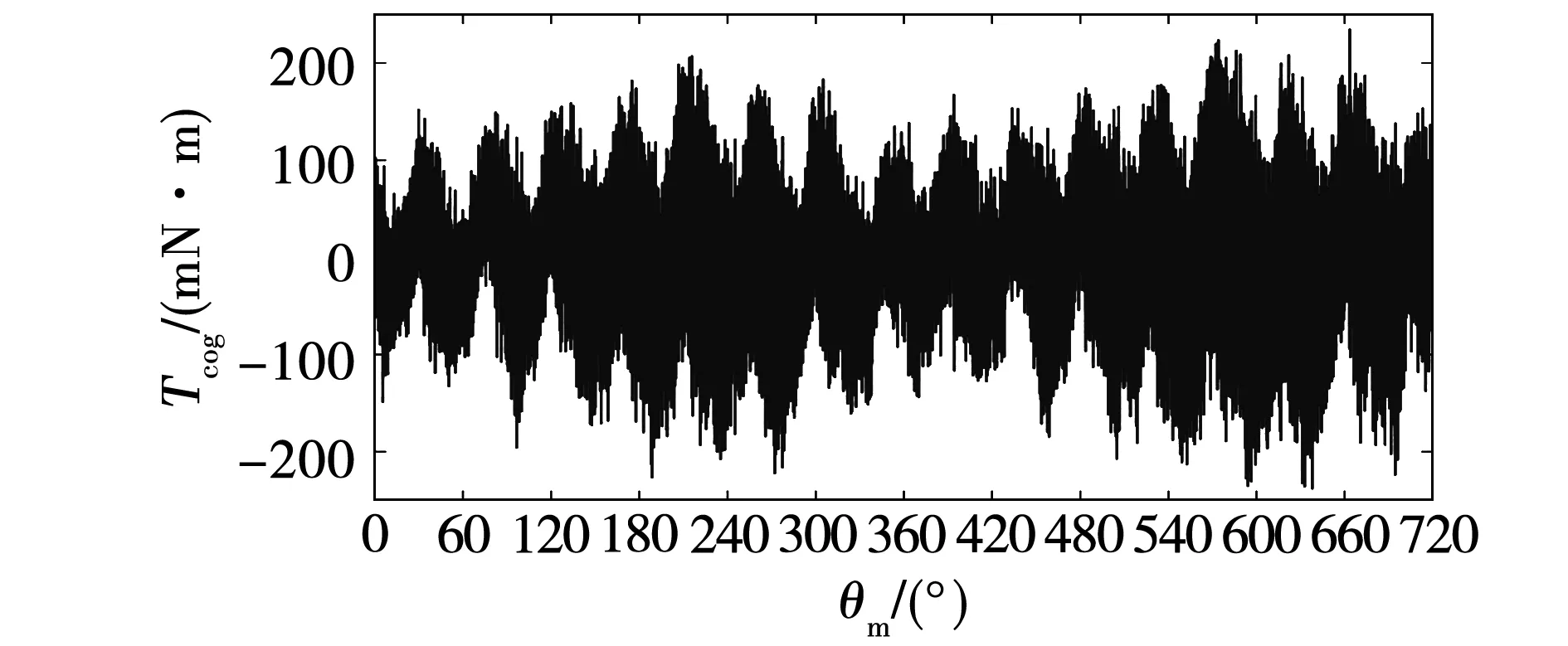
圖8 齒槽轉矩

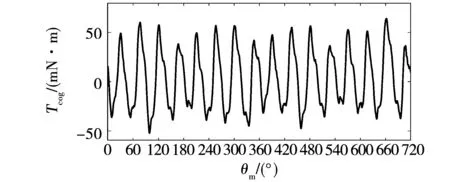
圖9 濾波后齒槽轉矩

圖9中的齒槽轉矩是兩轉的齒槽轉矩，由于齒槽轉矩大小只與轉子位置角有關，因此前后兩轉齒槽轉矩在相同位置角處大小應一致。圖10為圖9前后兩轉相同轉子位置處齒槽轉矩對比圖，可以看出，前后兩轉齒槽轉矩分布規律一致，只是在部分位置幅值存在很小的誤差，這主要是前后兩轉轉速大小不一樣，且計算過程忽視了阻尼系數引起的。

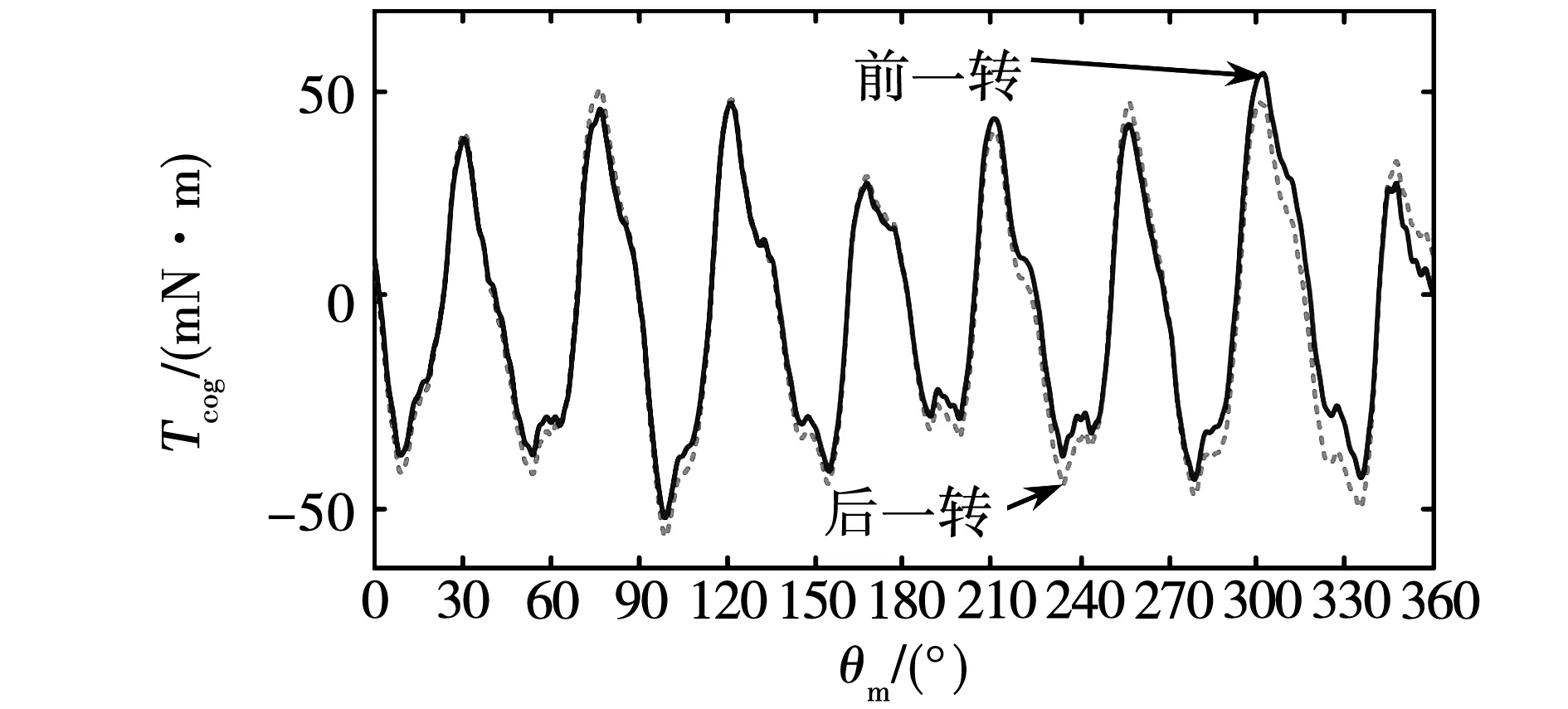
圖10 齒槽轉矩對比

對低通階次濾波后取出的5 000個數據進行角域傅里葉變換得到其階次譜如圖11所示，可以看出，齒槽轉矩諧波主要為定子缺陷引起的8及其倍數次、轉子缺陷引起的12及其倍數次，分別與式(3)、式(4)相對應，其中諧波幅值最大為第8階諧波的38.55 mN·m。但階次譜中還存在幅值稍大的6階，這主要是由于定子的6個輔助齒拼接處附加氣隙均不一樣，定子結構就會失去原有幾何對稱性，定子在整個圓周上幾何地重合6次，因此電機可被視為6個齒[20]，根據式(4)可產生6倍頻。其中同時滿足式(2)～式(4)的階次如24階為非理想條件下定子缺陷、轉子缺陷和理想條件下的齒槽轉矩共同作用引起的。此外，在低頻處還含有一些幅值較小的低頻成分，這主要是由轉子不對中、轉子偏心、磁漏等引起的。

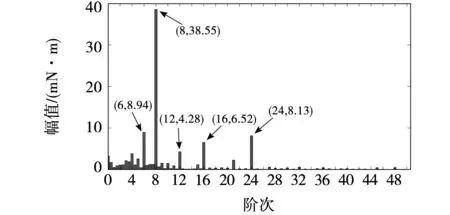
圖11 齒槽轉矩階次譜

為了保證實驗具有可重復性，在相同實驗條件下共進行5次實驗，此外，為觀察不同實驗條件下測量結果的變化，將砝碼質量由62 g換為65 g，再次進行5次相同的實驗。兩種砝碼質量下共10組數據，分別對其進行階次濾波和角域傅里葉變換，得到各次實驗主要階次幅值大小如圖12所示。

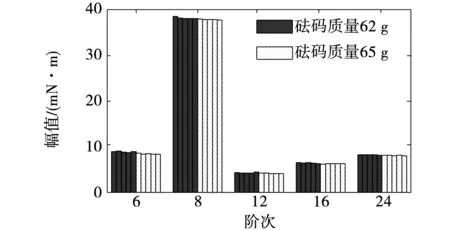
圖12 實驗結果對比

測試結果表明，該電機的齒槽轉矩諧波階次主要為6、8、12、16、24階，其中由定子缺陷引起的第8階諧波幅值最大，為38.55 mN·m。

由于計算過程忽略了阻尼力，因此取10組實驗中各階次最大幅值作為基準，得到砝碼質量分別為62、65 g時的各5次及總共10次實驗的最大相對誤差(rmax)如表2所示。由表可知，在相同實驗條件下和不同實驗條件下各階次幅值大小都會存在相對誤差且第6、12、16、24階相對誤差比第8階的大。此外，砝碼質量變大后，相對誤差也變大。造成上述誤差的原因主要是：1)相同實驗條件下每次實驗砝碼下落過程中的輕微擺動或轉動情況不一樣，導致轉速波動存在偏差；2)砝碼質量變大，轉速升高，阻尼力會變大，而根據式(12)計算齒槽轉矩時忽略了阻尼力；3)第6、12、16、24階幅值小，其相對誤差對幅值變化比較敏感。

此外，由表2可知，在砝碼質量為62 g時，各階相對誤差都不超過5%，因此選擇盡可能小的砝碼質量可減小測量誤差。

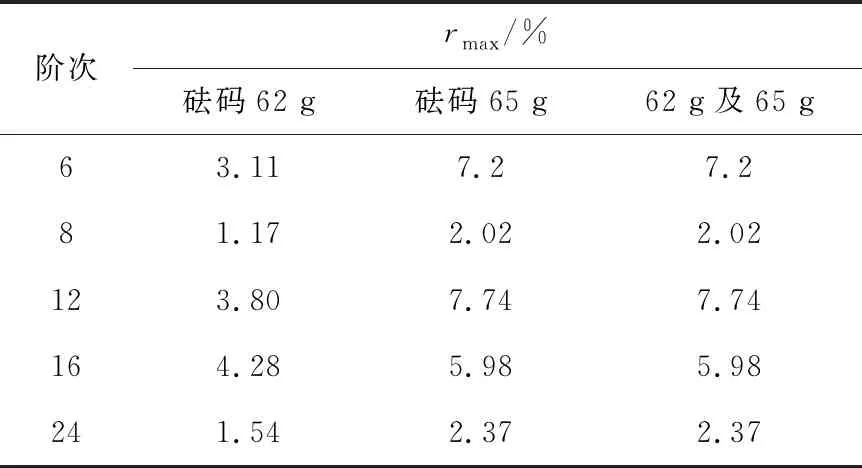
表2 最大相對誤差

4 測試結果驗證

當前齒槽轉矩測量方法中精度比較高的是直接測量法中的步進電機靜態測試法，但該方法需要高精度的扭矩傳感器及其數據采集分析系統、步進電機及其驅動系統，并且需要搭建安裝測試電機、扭矩傳感器及步進電機的試驗臺且安裝要求比較高。此外，當前沒有一個完全能夠精確測量出齒槽轉矩的方法，每種方法都會存在一定誤差，即使用同一種方法對同一個電機進行測量，所使用的傳感器靈敏度不同、試驗臺安裝不同，其測量結果也可能會產生比較大的誤差。綜上所述，加之時間及實驗條件有限，在此沒有與其他測試方法的測量結果進行對比，而是在矢量控制實驗平臺上采集電機的轉速進行諧波分析，并基于文獻[21]在MATLAB中建立與實驗平臺相對應的永磁同步電機矢量控制模型，以第3節中測量的齒槽轉矩諧波幅值及階次作為輸入，仿真得到同階次的轉速諧波幅值大小，并與實驗結果相比較，從而間接驗證所測齒槽轉矩階次的準確性及幅值大小的精度。

為了驗證第3節實驗所測的齒槽轉矩諧波階次的準確性，采集矢量控制下電機的不同轉速進行轉速諧波分析，并分析諧波階次組成、產生原因及與齒槽轉矩諧波的關系。

實驗平臺如圖13所示，為了排除負載波動及聯軸器不對中引起的轉速諧波，實驗時斷開了電機與聯軸器及磁粉制動器的連接，采集空載狀態下的轉速并做角域傅里葉變換得到階次譜如圖14所示。由圖11可知所測齒槽轉矩24階之后幅值很小，因此就只分析轉速階次譜的前24階。從圖14可以看出，不同轉速諧波階次主要為6、8、12、16、24階諧波，且第8階諧波幅值最大。此外，還有低于6階的幅值較小的諧波成分。

圖13 實驗平臺

實際控制中轉速諧波產生的主要原因有：1)逆變器死區效應及永磁體磁鏈諧波引起6kp次轉速諧波，實驗電機極對數p=4，死區效應及永磁體磁鏈諧波引起的轉速諧波階次為24及24的整倍數次；2)磁漏、轉子偏心及負載轉矩；3)齒槽轉矩。

由于轉速是在空載條件下采集的，因此沒有負載及軸不對中引起的轉速諧波，可知轉速譜中低于6階的諧波主要是由漏磁及電機轉子偏心引起的。綜上分析并結合圖11齒槽轉矩階次譜與圖14轉速階次譜，可得出結論：轉速諧波中的6、8、12、16次諧波由齒槽轉矩引起，并且齒槽轉矩幅值最大的第8階引起的轉速諧波第8階幅值也最大；24階諧波是由齒槽轉矩、逆變器死區、永磁體磁鏈諧波共同作用引起的。

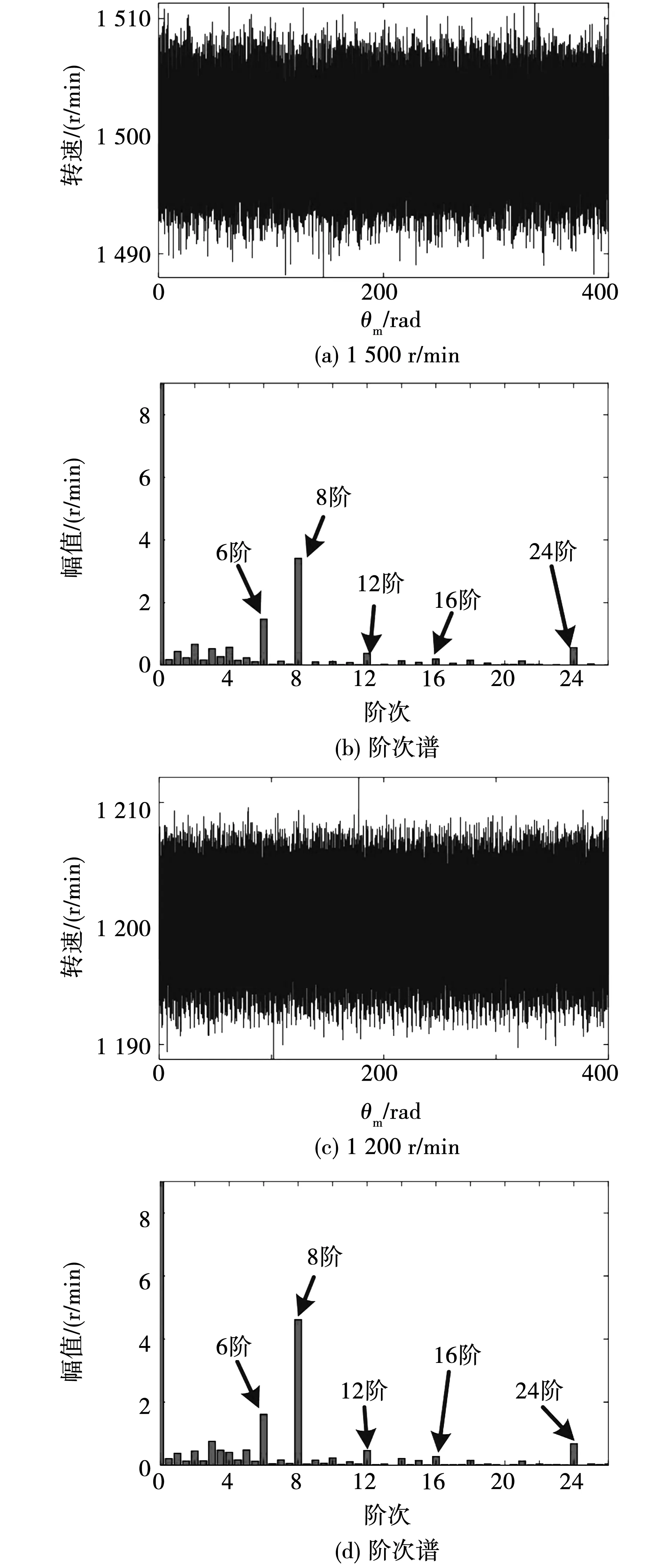
圖14 轉速及轉速階次譜

文獻[18]建立了矢量控制下永磁同步電機精確的傳遞函數模型，研究了死區效應引起的電壓誤差到d-q軸電流響應的閉環傳遞函數且理論計算、仿真和實驗結果一致。為了進一步驗證第3節所測齒槽轉矩諧波幅值精度，基于文獻[18]在MATLAB中建立與圖13實驗平臺相對應的永磁同步電機仿真模型如圖15所示，由于齒槽轉矩直接作用在電機轉子上，其作用等效于負載諧波，因此在仿真模型中把所測齒槽轉矩施加在電機負載輸入端，仿真得出相應的轉速諧波幅值，并與電機實際齒槽轉矩引起的轉速諧波幅值比較，從側面驗證所測齒槽轉矩與電機實際齒槽轉矩的誤差。

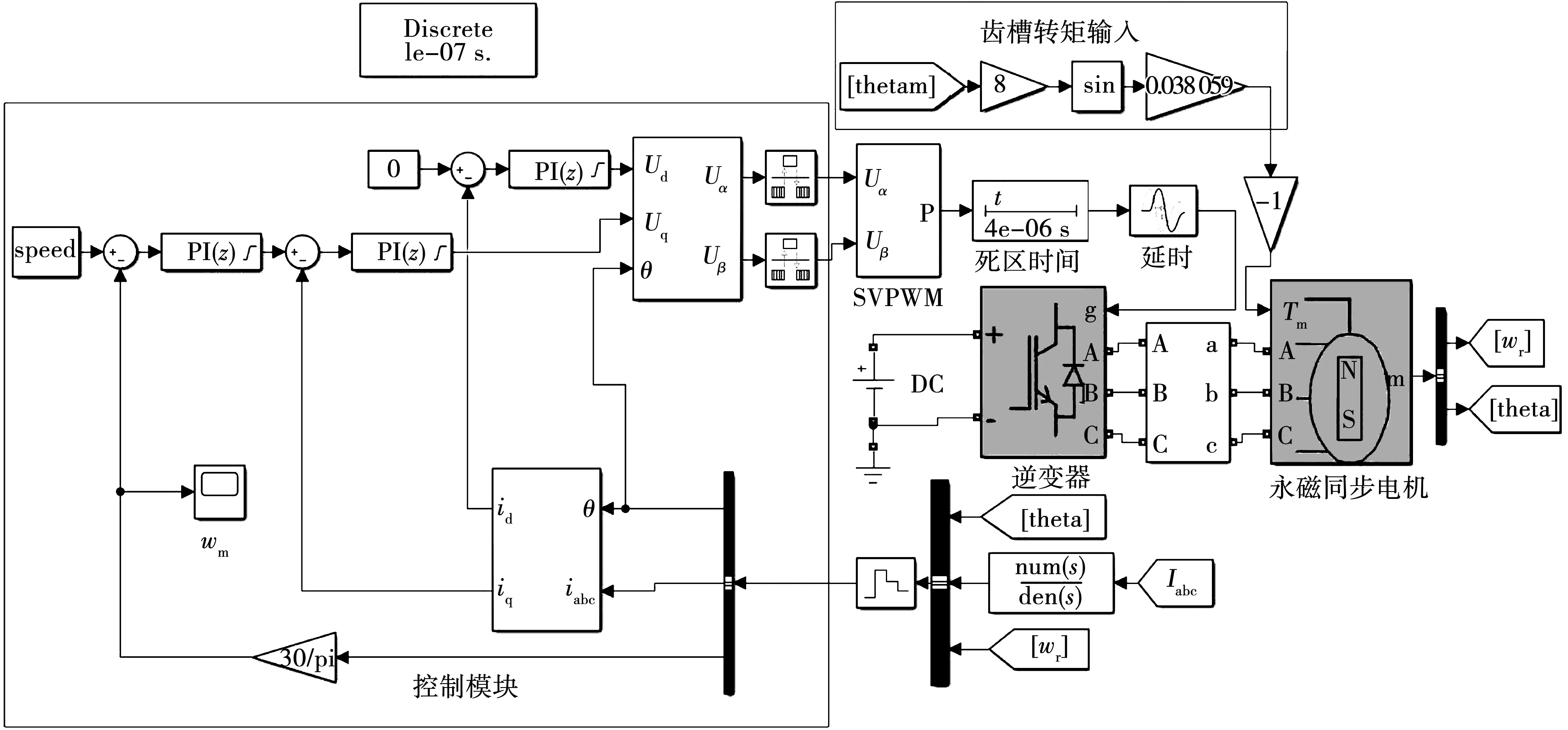
圖15 仿真模型

由于本文與文獻[18]中的實驗平臺為同一實驗平臺，電機也為同型號的電機，控制系統參數也一致，因此保證了仿真模型的準確性。

由圖11可知齒槽轉矩諧波第8階幅值最大，其他階次幅值均小于10 mN·m，且隨著諧波階次的增大，其對轉速諧波的影響也逐漸變小，在低頻部分轉速諧波會受到聯軸器對中的影響而產生轉頻的倍數次諧波，因此，為排除其他因素的影響，在此主要驗證第8階齒槽轉矩諧波幅值。首先以所測第8階齒槽轉矩諧波幅值平均值38.059 mN·m和其階次作為輸入，仿真得到同階次轉速諧波幅值，并與實驗得到的第8階轉速諧波進行對比。仿真和實驗的相關參數一致，運行工況如表3所示。

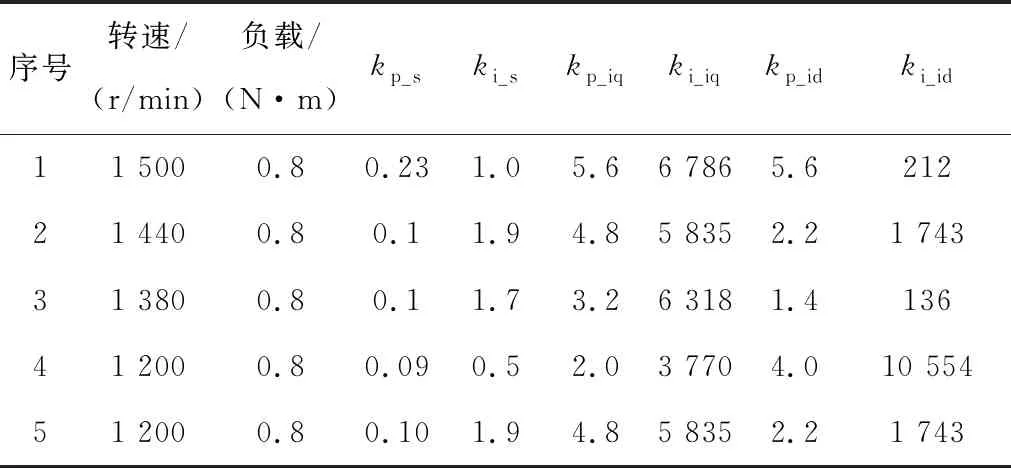
表3 運行工況及PI參數

圖16為表3中第1、2組工況仿真和實驗所得的轉速譜。實驗結果可以看出轉速在低頻部分存在轉頻的倍數次諧波，這主要是聯軸器對中不好引起的，但對中引起的轉速諧波在第4階以后幅值就很小，所以其對第8階的影響也可忽略不計。圖17為根據表3得到的仿真和實驗結果對比圖，二者結果相吻合，其中實驗和仿真的最大相對誤差為14.4%，最大絕對誤差為0.33 r/min，對應第1組結果，該組相對誤差較大的原因主要是該組轉速諧波幅值相對較小，因此相對誤差就凸顯得比較大。引起絕對誤差的主要原因是測量的齒槽轉矩和實際齒槽轉矩之間存在誤差及仿真所用電機參數與電機實際的參數也存在一定誤差，因此在不同轉速和不同PI參數下會引起不同的轉速誤差。綜上可知，本文所提的齒槽轉矩測量方法具有較高的精度，可滿足實際工程應用。

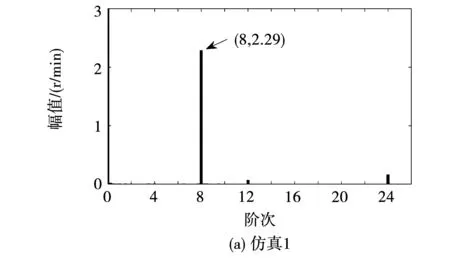
圖16 仿真與實驗結果

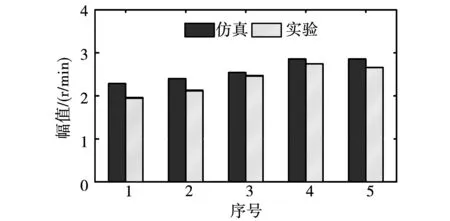
圖17 仿真和實驗結果對比

5 結 論

首先，分析了永磁電機齒槽轉矩在理想與非理想條件下的頻率特性；其次，從設計原理出發，提出了一種簡單快捷、成本低的永磁電機齒槽轉矩測試方法，并對一臺8極12槽永磁同步電機進行實驗測試，對計算出的齒槽轉矩進行低通階次濾波得到齒槽轉矩角域波形，利用角域傅里葉變換獲取其階次成分及幅值，得到其主要階次為6、8、12、24，且第8階幅值最大為38.55 mN·m，并結合理論及實驗電機定轉子結構分析了各階次產生的原因。此外，通過分析實驗的相對誤差可知，合適的砝碼質量可以減小測量誤差；最后，通過對比仿真和實驗結果，得出所測齒槽轉矩和實際齒槽轉矩引起的轉速諧波幅值最大絕對誤差為0.33 r/min，表明所測齒槽轉矩具有比較高的精度。

該研究成果可測出電機齒槽轉矩諧波成分及幅值大小，進而用于：1)評價實際電機理想與非理想條件下齒槽轉矩性能指標；2)在大批量制造前，對同種型號的電機結構進行優化以減小理想與非理想齒槽轉矩；3)測出輸入電機控制系統的齒槽轉矩諧波階次及幅值，進而可通過控制方法如諧波注入等來減小齒槽轉矩引起的轉矩、轉速諧波等。