淺析數形結合思想在小學數學教學中的應用

付紅波

摘 要：數形結合既是一種重要的數學思想，又是一種常用的數學方法，在小學數學教學中廣泛應用，本文介紹相關概念并結合人教版小學數學教材，初步整理了數形結合思想方法在各教學領域的滲透與應用。

關鍵詞：小學數學;數形結合

數形結合思想是小學數學中的一種重要思想。它是在數與形之間的本質聯系上，以“形”直觀的表達數，以“數”精確的研究形的思想方法。在數形優勢互補的基礎上，把抽象的數量關系與直觀的圖形結構結合起來，使數量的精確刻畫與空間形式的直觀形象巧妙、和諧的結合在一起。充分利用這種結合，尋找解題思路的一種思想。利用數形結合思想可以解決許多數學問題。數學家華羅庚說：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔離分家萬事休”。利用樹形結合能使“數”和“形”結合起來。以形助數、以數輔形，可以使許多數學問題變得簡單化。那么如何在教學中有效滲透數形結合的思想，下面就結合我的教學實踐談一些粗淺的認識。

一、以形助數，化抽象為直觀

1.刻畫概念本質

例如：在教學《義務教育教科書》（人教版）三年級數學上冊《倍的認識》這一課時。可以利用圖形直觀的呈現兩個量之間的倍數關系，讓學生在兩組圖形的觀察比較中由“幾個幾”轉化為“倍”，借助幾何直觀把復雜的數學問題變得簡明、形象，使學生對“倍”的認識由淺入深，對“倍”的感性認識上升到理性認識，最終建立“倍”的概念。

再比如四年級下冊《小數的意義》的學習中，小數是一個十分抽象的概念，它與分數相比更加抽象。我們同樣是通過數與形的結合，幫助學生理解掌握小數的意義、小數的大小、小數的性質。通過1米=10分米，讓學生理解1分米=0.1米，并類推出1厘米=0.01米，1毫米=0.001米;通過數與形完美的結合——數軸，讓學生理解小數的組成、小數大小的比較、小數與整數的關系等。總之，這種數形結合直觀的幫助學生進行對比、理解，使學生在自我思維里清晰的刻畫了概念的本質。

2.明晰數量關系

數形結合不僅是一種數學思想，也是一種很好的學習方法。把數量關系和空間形式結合起來去分析問題、解決問題，這就是數與形結合思想。教學中引導學生應用數形結合的思想可以把復雜問題簡單化，把抽象思維具體化，把數量具體化、清晰化、量與量之間的關系就更清晰。

例如：畫圖解決分數應用題

新人教版數學六年級上冊第16頁練習三

第5題：雞的孵化期是21天，鴨的孵化期比雞長。鴨的孵化期是多少天？

要解決這個問題，需要理解雞和鴨孵化期的數量關系，但單憑文字，數量關系就比較抽象，這個時候借助畫圖可以化繁為簡、變抽象為直觀，明晰了兩個量之間的數量關系。

如圖：

雞的孵化期：

鴨的孵化期：

從圖上直觀的看出鴨的孵化期是雞的，解決雞的是多少就是鴨的孵化期。通過這樣的畫圖分析，使學生明了了兩個量之間的關系，并輕松的解決了這樣難以理解的問題。以后學生可以利用這樣的方法，分析問題并解決問題。

又如：新人教版數學三年級上冊有關倍的內容

小強買7本筆記本，用去了35元。買9本同樣的筆記本，一共需要多少錢？

解決買9本需要多少錢，對于邏輯思維差的學生來說，是難以解決的。這個時候借助畫圖，能讓學生清晰的看出把35元平均分成7份，每份就是一本的價格，根據一本的價格從而解決9本多少錢這個問題。

從圖中可以看出7本一共35元，1本就是5元，那么求9本多少錢，其實就是就9個5是多少。通過畫圖，使學生直觀的看出要先解決單價，才能明晰求9本多少錢其實就是求9個5也就是5的9倍是多少。

3.直擊問題本質

數形結合能把抽象性問題清晰化，便于觀察，并直擊問題的根源和本質，運用數形結合的思想來解決問題，揭示問題的本質，可促進學生形象思維和抽象思維的協調發展，更能促進學生的可持續發展。

例如：“植樹問題”。在一條20米的小路上植樹，每隔5米植一棵，可以植多少棵？

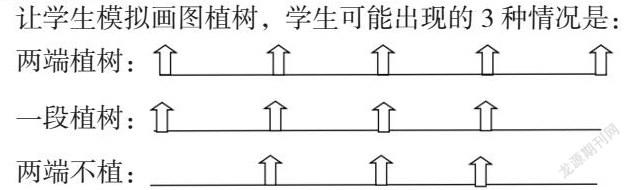
讓學生模擬畫圖植樹，學生可能出現的3種情況是：

兩端植樹：

一段植樹：

兩端不植：

學生通過圖形的觀察建立了棵數和段數之間的聯系，并通過理解探索出棵數和段數之間的聯系——歸根結底就是一一對應的關系，既棵數和段數一一對應。兩端植樹就是棵數和段數一一對應后，還剩一棵樹，棵數=段數+1。只植一端就是棵數和段數剛好一一對應，棵數=段數。兩端都不植段數和棵數一一對應后，段數比棵數多1，棵數=段數—1。通過數形結合這樣的方式，揭示了問題的本質，使學生更易理解，樹立了學生的數學自信，提高了學生的邏輯思維能力。

二、以數輔形，拓展思維

“形”的優勢是直觀形象，但缺少“數”的精準刻畫，就難以準確表達。所以以簡潔的數學描述、形式化的模型才能更好的體現數學抽象化和形式的魅力。

比如對幾何圖形的判斷：比較周長相等的長方形和圓，哪個圖形的面積大？如果僅僅圖形的對比很難辨別出哪個的面積大，這個時候就需要“數”的精準刻畫。假如兩個圖形的周長都是20厘米，那么正方形的面積等于（20÷4）2=25平方厘米，圓面積等于3.14X（20÷6.28）2≈31.8平方厘米。比較31.8>25，由此得出圓的面積大。這樣通過具體的數量之間的對比由此得出正方形和圓在周長相等的情況下，圓的面積大。所以正如數學家華羅庚說：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔離分家萬事休”。只有“數”與“形”有機的結合，才能詮釋其數形結合的魅力。

總之，數形結合思想是將抽象的數學語言與直觀圖形結合起來，使抽象思維與形象直觀結合起來，讓數學思維直觀的表達，更便于理解、分析、解答問題。所以數形結合不僅能使概念本質化、解題過程簡單化、學生學習主動化，還能發展學生的空間觀念和形象思維，更好地展現知識的建構過程。教師在教學中有機的滲透數形結合思想，能激發學生的學習興趣，提高學生的數學思維能力和數學素養，促進學生情感、態度、價值觀的發展。

參考文獻：

[1]林麗靜. 淺析數形結合思想在小學數學教學中的應用策略[J].2021.

[2]何麗巖. "淺析數形結合思想在小學數學教學中的應用."（2019）.