岸邊集裝箱起重機有限元建模與模型修正*

李益波 肖炳林 何威譽 劉嘉輝 秦仙蓉

1廣州港集團有限公司 廣州 510100 2廣州港股份有限公司南沙集裝箱碼頭分公司 廣州 511462 3同濟大學機械與能源工程學院 上海 201804

0 引言

岸邊集裝箱起重機（以下簡稱岸橋）是集裝箱碼頭前沿裝卸集裝箱船舶的重要設備，長期遭受環境侵蝕及循環荷載作用，獲取結構狀態并進行健康監測對維護岸橋結構安全顯得尤為重要。通常結構健康監測系統通過采集監測數據得到岸橋結構響應，而隨著集裝箱港口自動化和船舶大型化的發展，對岸橋結構特性也有更高的要求，需要建立精準的有限元模型校核岸橋性能。由于建模過程中的簡化和假設，以及材料、施工等眾多不確定性因素，使得有限元模型計算的結構響應與監測數據獲取的結構響應存在一定的偏差，需要利用監測數據對有限元模型進行修正[1]。

目前，常見的模型修正方法主要分為2類：按修正對象主要分為矩陣型修正法和參數型修正法；按修正的試驗依據分為基于靜力的模型修正法和基于動力的模型修正法[2]。結構監測領域中，通過監測數據分析得到結構頻率，以此為修正目標修正有限元模型的材料參數，使基于動力模型修正方法得到了廣泛應用。李曉婭等[3]基于中小跨徑混凝土梁式橋梁監測數據，提出了適合中小跨徑混凝土梁式橋有限元模型修正的技術。李元吉等[4]對復雜桿系拱橋結構進行有限元建模，提出基于監測數據的系桿拱橋有限元模型修正方法。徐志強等[5]建立某桁架拱橋初始有限元模型，基于振動監測數據對其初始模型進行修正。閆濤等[6]建立了上海長江大橋斜拉橋的有限元模型，基于長江大橋主航道斜拉橋健康監測系統的監測數據對有限元模型進行修正。

參考上述基于監測數據的有限元模型修正相關文獻，本文以某港口岸橋為例，建立其初始有限元模型，基于監測數據識別岸橋模態頻率，并以有限元計算頻率與識別頻率殘差為修正目標對建立的岸橋初始有限元模型進行修正。結果表明修正后模型的頻率更加接近實測頻率，具有工程實用價值。

1 基本理論

1.1 靈敏度分析方法

靈敏度是結構物理參數變化引起結構模態參數變化大小的度量。假設N個自由度的結構動力方程為[7]

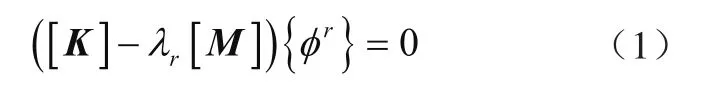
式中： [K]為剛度矩陣，[M]為質量矩陣，λr為第r階特征值，｛r｝φ 為第r階振型。根據式（1）對設計參數Pi(i=1，2，…，n)求偏導，并結合[K]、[M]的對稱性以及正交條件，可得特征值的一階靈敏度為[8]

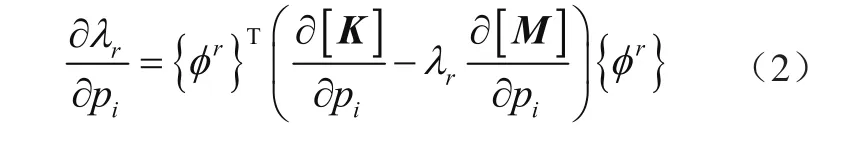
對式（2）求解，則第i個特征向量對參數Pi的偏導數可表示為特征向量的線性組合為

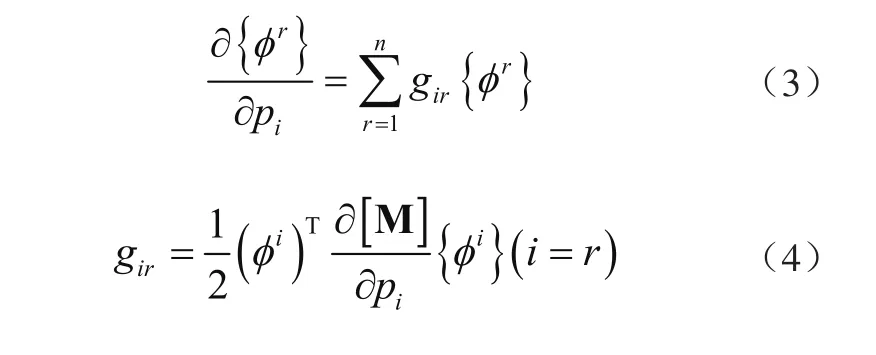
式中：系數gir為模態振型對參數Pi的解析靈敏度。

1.2 頻域分解法模態參數識別

頻域法參數識別是由傅里葉變換而不斷發展起來的，具有直觀、處理效率較時域法更高、且受噪聲的影響較小等優點。其中頻域分解法（Frequency Domain Decomposition，FDD）應用廣泛，該方法可有效地識別系統的固有頻率和模態振型，對密集模態具有較高的分辨率。

假設激勵為白噪聲激勵，系統的輸入、輸出功率譜密度 GXX( jω)與 Gyy( jω)滿足[9]

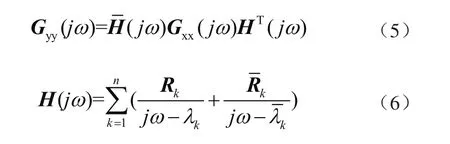
式中：H ( jω)為頻響函數矩陣，n為模態階數，λk為第k階極點，Rk為第k階留數矩陣。

將式（6）代入式（5）為

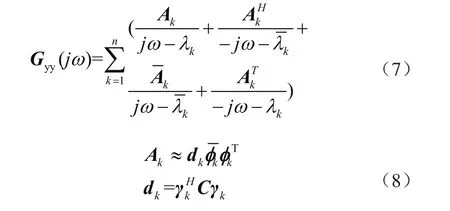
式中：Ak為相關的留數項，在小阻尼情況下，第k階模態附件的表達式。dk為常數項，φk為第k階模態振型矩陣，rk為模態參與向量。

因此，對于小阻尼系統，其響應的PSD可表示為

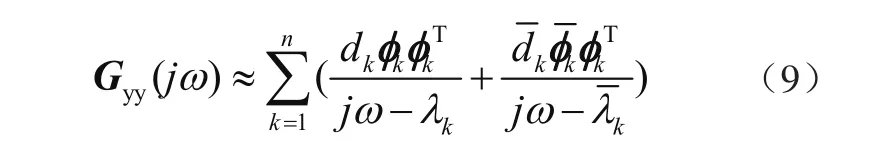
FDD法首先對監測數據進行譜估計，然后在離散頻率點對譜估計進行奇異值分解為

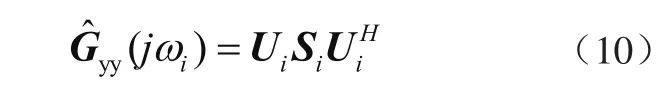
將系統頻率的功率譜矩陣進行奇異值分解后，第一個奇異值的峰值位置為該系統第k階的固有頻率，該奇異值對應的奇異值向量矩陣即為第k階模態振型。

2 基于監測數據的有限元模型修正方法

建立岸橋初始有限元模型，對初始有限元模型進行修正。設待修正的岸橋結構目標函數為，目標函數的選取指標有很多，通常頻率、振型及模態柔度等指標較為常用。頻率能反映結構整體動力性能，可選取監測數據識別頻率與有限元計算頻率的殘差作為目標函數fr，則有限元模型修正目標可表示為

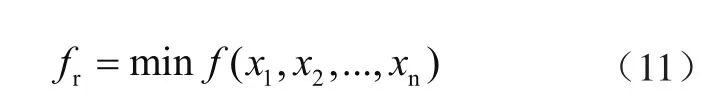
式中：x1,x2, ...,xn為待修正的設計參數變量，模型修正方法流程如圖1所示。

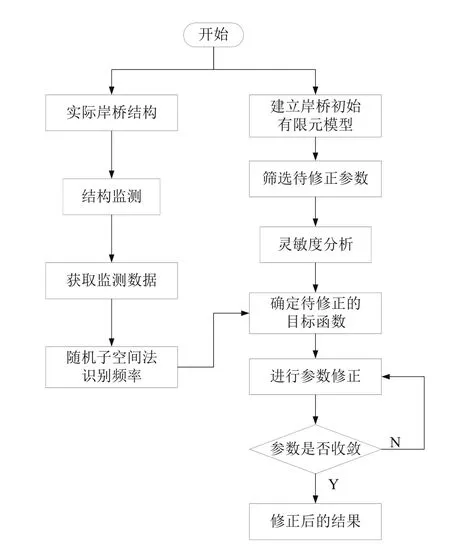
圖1 基于監測數據的模型修正流程

3 岸橋有限元建模與模型修正

3.1 岸橋初始有限元建模

以某港口岸橋為例，整機高約84 m，前大梁長約76 m，后大梁長約32 m，對實機岸橋結構進行有限元建模。岸橋的主體結構采用梁單元Beam 189建模；門框撐桿、拉桿系統采用桿單元Link 10建模；小車及吊具、機器房等構件以集中質量點單元Mass 21的方式分別添加在大梁及聯系橫梁相應位置，模型如圖2所示。

圖2 岸橋結構有限元模型

對建立的有限元模型進行模態分析，取岸橋前4階頻率及振型，結果如表1所示。按照前文模型修正流程，獲取岸橋結構監測系統中各個振動測點的監測數據，利用FDD法識別得出岸橋模態頻率，并結合表1結果計算出誤差（（分析值-實測值）/實測值），如表2所示。

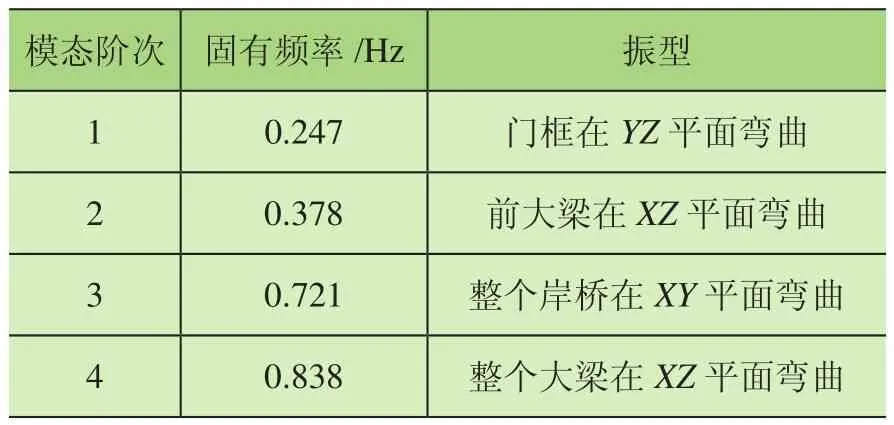
表1 岸橋模態分析結果

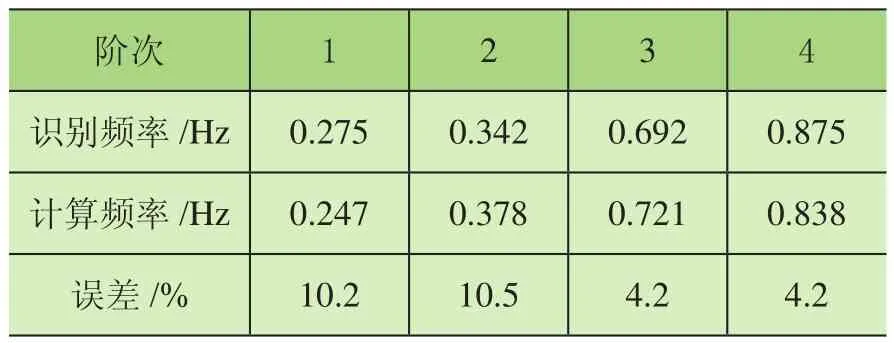
表2 岸橋實測頻率與計算頻率對比值

由表2可知，有限元模態分析結果和監測數據識別結果的各階振型相關性較高，這表明建立的有限元模型較準確，但也反映出相應模態頻率的誤差最高超過10%，且均為負值，說明材料特性建模不準確。以表2中的頻率值作為岸橋有限元模型修正的目標函數對岸橋有限元模型進行修正。

3.2 修正參數選擇

根據實際工程經驗，初步選擇岸橋13個參數進行靈敏度分析：1為前大梁的彈性模量，2為密度，3為陸側立柱截面長度，4為陸側立柱截面寬度，5為海側立柱截面長度，6為海側立柱截面寬度，7為前大梁長度，8為前大梁截面寬度，9為后大梁截面寬度，10為陸側上橫梁截面寬度，11為海側上橫梁截面寬度，12為海陸下橫梁截面寬度，13為門框聯系橫梁截面寬度。對所選的13個參數做靈敏度分析，如圖3所示。

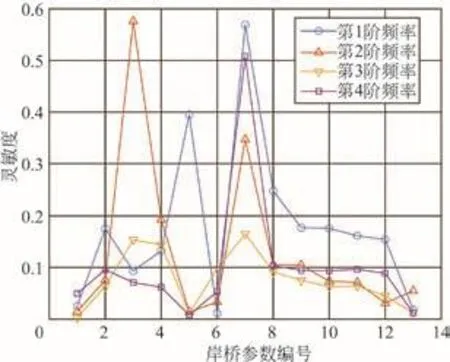
圖3 岸橋各階模態頻率對結構參數靈敏度

由圖3可知，序號3，4，5，7，8參數靈敏度較大，故選擇這5個參數作為優化變量，如表3所示。由表1可知，岸橋結構前四階的振型主要為前大梁和門框的彎曲，故選擇岸橋模型的優化變量是合理的。

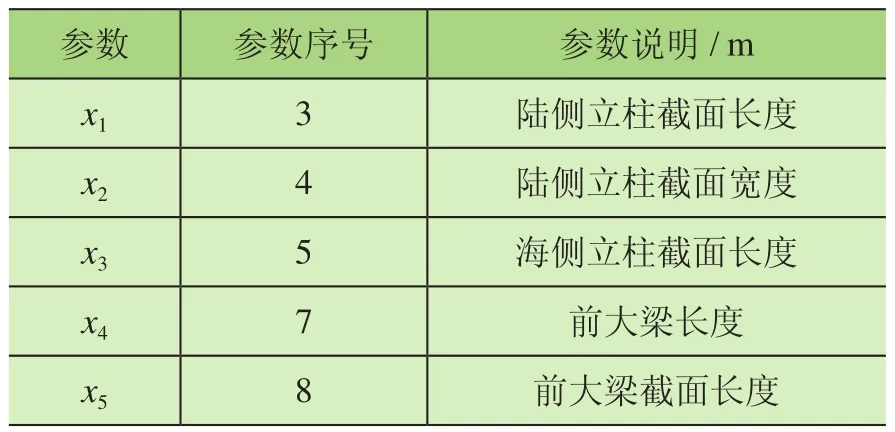
表3 岸橋有限元模型待修正優化變量

3.3 模型修正結果

使用Matlab中的Fmincon函數對岸橋有限元模型進行修正。修正前對所選擇的5個參數進行歸一化處理，參數的變動范圍限制在，修正的收斂曲線如圖4所示。由圖4可知，在修正過程中的收斂曲線在第13次迭代時收斂，5個參數修正值如表4所示。由表4可知，岸橋5個參數的修正率較為接近，僅x2參數修正率略大，可表明文中所提出修正方法的可行性，修正后的頻率值如表5所示。

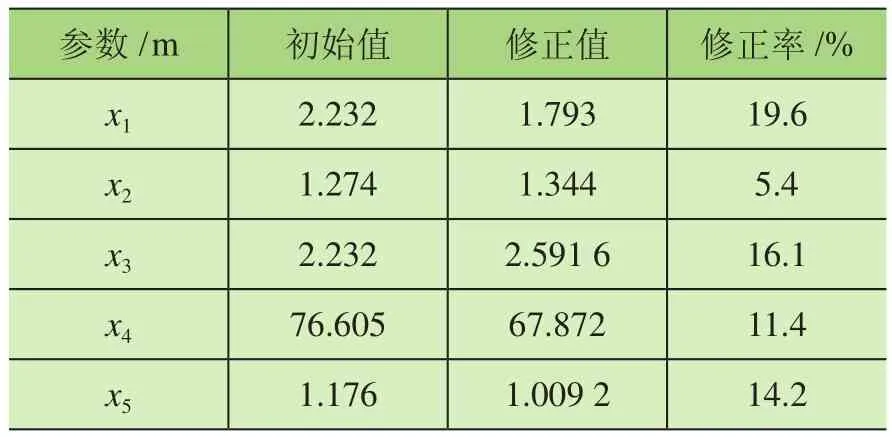
表4 岸橋修正前后設計變量結果對比

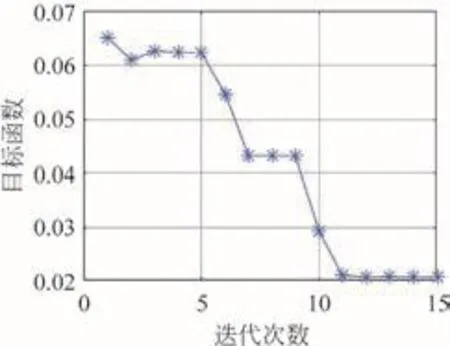
圖4 修正收斂曲線

通過表5和表2對比可以看出，修正前岸橋結構前4階模態頻率與真實值的誤差較大，最大頻率誤差達到了10%以上。通過模型修正后，前4階頻率的誤差均降低至2.6%以下，修正后的模型精度明顯提高，表明有限元模型進行修正的可行性和有效性。

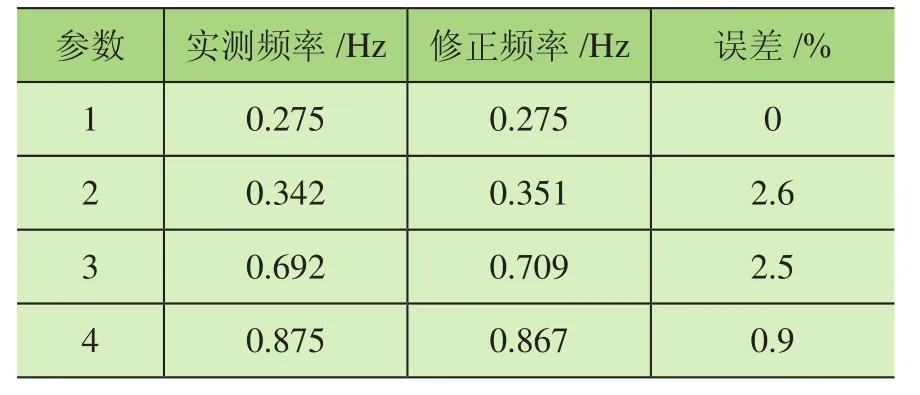
表5 模態頻率修正前后結果對比

4 結論

本文以某港口岸橋為例，首先建立了岸橋的初始有限元模型，對初始有限元模型進行模態分析；其次根據監測數據的識別模態頻率，在此基礎上對各模型參數進行頻率靈敏度分析，選擇對頻率影響大的參數進行模型修正；最后以計算頻率與識別頻率的殘差為修正目標對模型進行迭代優化，得到修正后的各參數值。結果表明經過修正后的模型各階頻率與實測值相比誤差明顯減小，模型精度明顯提升，修正后的模型可進一步用于健康監測后續分析及應用。