關鍵問題：有效備課的新探索

文|杜麗麗

一、“關鍵問題”有效備課的內容

“三備教學設計”由備教材、備學生、備自己三要素構成，“關鍵問題”有效備課設計的“三備教學設計”新模板充分體現生本理念，聚焦“關鍵問題”，推進課堂變革。從如何設計“關鍵問題”備課導引，形成備課新理念和如何破解“關鍵問題”，構建備課新策略入手，形成“關鍵問題”有效備課的新方法和新架構，促使教師真備課、備真課、真思考、真研究。

二、“關鍵問題”有效備課的實施策略

1.確定“關鍵問題”的技術路徑。

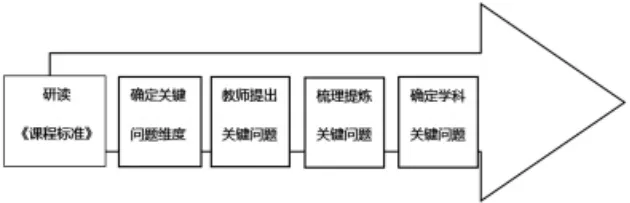
在教學設計中，根據關鍵問題設計相應的學習活動。

2.梳理“關鍵問題”的內容。

確定數學關鍵問題的維度，結合《數學課程標準（2011年版）》內容中闡述的十大核心詞，提煉梳理數學核心素養十大內容的關鍵問題。見下表。

3.提煉“關鍵問題”的新策略。

（1）前置作業設計提煉關鍵問題。

項目組開展了前置性作業設計與關鍵問題提煉的實踐與思考。以五年級上冊第六單元《多邊形的面積》整理與復習一課為例：

前置性作業核心：

適當的量——體現減負提質

適當的度——追求低入高出

維度 數學關鍵問題數感1.如何在現實情境中培養學生數感？2.如何讓學生通過操作和探究培養學生的數感？3.如何讓學生在具體問題解決中鞏固和深化數感形成？符號意識1.如何在具體情境中滲透符號意識？2.如何喚醒學生的符號意識，體會符號優越性？3.如何在解決問題過程中逐步建構符號模型體系？空間觀念1.如何引導學生在觀察的基礎上引導學生概括和表述？2.如何引導學生把幾何知識運用于各種具體問題中？3.如何引導學生進行有效操作達到培養學生的空間觀念？幾何直觀1.如何借助實物、模型、圖形及多媒體等手段幫助學生積累豐富的幾何表象？2.如何調動學生多感官參與對幾何形體的研究，增強學生的幾何直觀能力？3.如何在聯想和想象中拓展學生幾何直觀思維空間？數據分析觀念1.如何通過數據收集，分析判斷體會數據中蘊涵的信息？2.如何對同樣的數據分析選擇合適的方法？3.如何通過數學分析體驗隨機性和規律？運算能力1.如何培養學生運算的算理和合理簡潔的運算能力？2.如何幫助學生深刻理解各種數的內涵？3.如何幫助學生深刻理解四則運算的意義？推理能力1.如何有機的融合在四大領域教學之中？2.如何借助熟悉的生活情境，發展學生的推理能力？3.如何關注推理能力的層次性和差異性？模型思想1.如何從多側面、多層次的現實問題原型為載體建立數學模型？2.如何在建模過程中對數學思想方法的提煉與體會？3.如何變換情境，引導學生運用模型解決問題？應用意識1.如何利用數學的概念、原理和方法解釋現實世界的現象？2.如何讓學生認識到現實生活中蘊涵著大量與數量和圖形有關的問題？3.如何把生活中的問題抽象成數學問題并用數學的方法予以解決？創新意識1.如何創設寬松、開放的教學環境激活學生的潛能？2.如何創設適當的問題情境培養創新意識？3.如何靈活應用知識解決問題，培養學生的高階思維？

前置性作業在鞏固共性的基礎上分享了差異。例如基于本單元“平行四邊形轉化成長方形，三角形轉化成平行四邊形，梯形轉化成平行四邊形”的學習路徑，多數學生會選擇記“平行四邊形”的面積公式。也有不少學生選擇了記“長方形”并清楚解釋了多邊形的面積計算都是以長方形面積計算為基礎。還有不少學生選擇“梯形”，他們對梯形的萬能計算公式十分感興趣，知道梯形的面積公式可以計算其他四種圖形的面積。

適當的點——圍繞關鍵性問題

本節課我們確定的關鍵性問題：如何引導學生進一步明晰面積公式推導過程，探究各種圖形的內在聯系？如何理解梯形面積公式為什么是萬能公式？

前置性作業的設計為本課提煉這兩個關鍵性問題而服務，打通了平行四邊形、三角形、梯形及組合圖形的內在聯系。

適當的線——鏈接課堂教學

教師以前置性學習作為課堂教學的啟動環節，引領學生找尋本節課的關鍵問題。分層次反饋：記“長方形”的——記“平行四邊形”的——記“梯形”的，在反饋中整理單元知識脈絡，使碎片化的知識整合融通，順利過渡到理解萬能公式、運用梯形公式快速比較五個圖形的面積。

從而引出整理復習課的練習環節：

挑戰一：你能有幾種方法求出涂色部分的面積。

挑戰二：下面哪幅圖的涂色部分可以用這個算式計算（ ）。

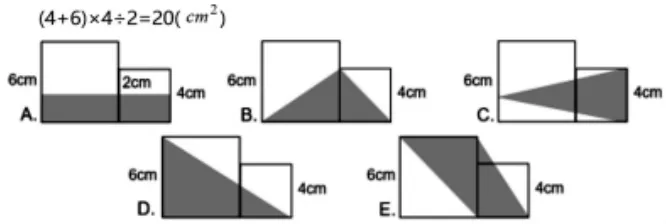
挑戰三：用這個算式計算的圖形還可以怎么畫？

（2）思維導圖提煉關鍵問題。

運用思維導圖“清序”

思維導圖備課以學生為出發點，圍繞“算、看、背、動”四個字對教材的知識結構進行重組，對知識的生長點進行定位。

以《筆算進位加法》為例：

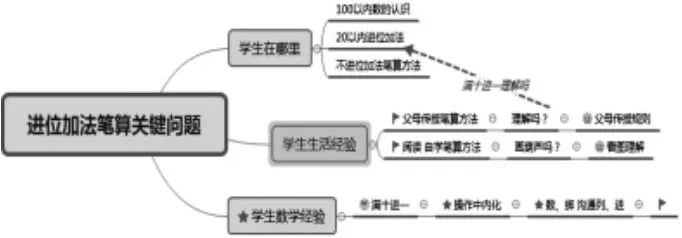
課前慎思：學生帶著什么知識來？又帶著什么知識離開呢？

思維導圖：基于生活經驗盤活——如何實現對“滿十進一”的理解。

解決策略1：擺小棒呈現5+7=12時，有什么辦法讓小伙伴一眼看出你擺了幾根小棒？通過將10根小棒扎成一捆，就自然而然地誕生“滿十”。這一捆應該放到哪里呢？水到渠成地解決了“進一”的問題。

解決策略2：設計五個層次的活動，調動所有感官讓“滿十進一”的過程吸收、內化。①動手擺；②動嘴說；③仔細聽：位值板上擺圓片過程；④動筆列；⑤回憶擺小棒、擺圓片的過程。通過這五個層次的多感官活動，幫助學生深刻理解“滿十進一”。

思維導圖：基于數學經驗——如何體驗先算個位再算十位的合理性。

解決策略:出示學生先算十位再算個位的錯例，讓學生猜測為什么該學生在十位進行涂改？讓學生感受進位加法時，先算十位，再算個位，對于“進一”的計算非常麻煩，進而認識到先算個位，再算十位的合理性。

運用思維導圖“盤活”

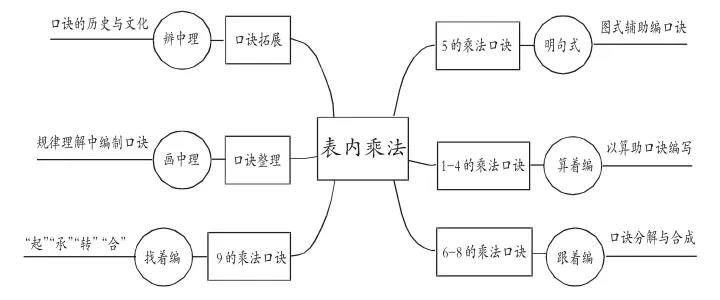
利用思維導圖聯結單元，豐厚對教材的解讀。以“表內乘法”為例，我們制作了這樣的思維導圖，分析整個單元知識前后關系。

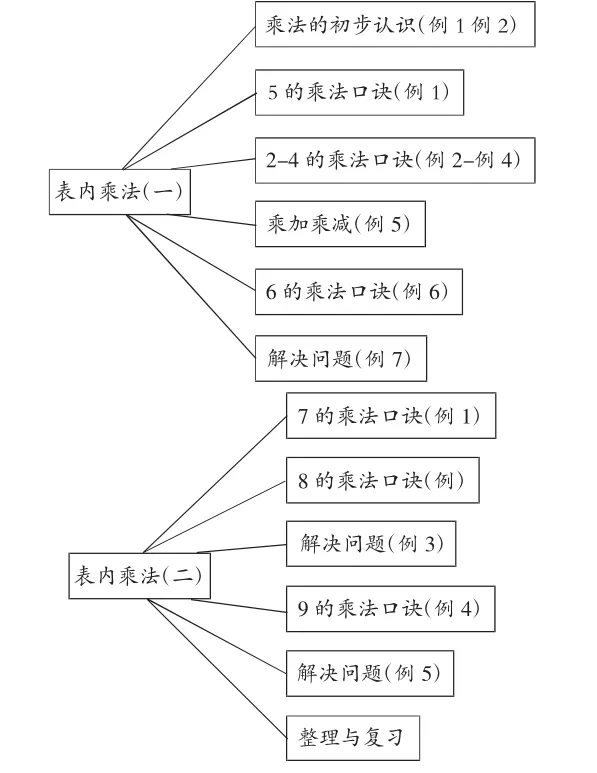
從思維導圖中我們發現教材是分單元進行編排。教材的口訣課時劃分實際上是對口訣表進行了橫向劃分。不同教材版本對比，人教版與蘇教版以橫向編排為特色，浙教版與北師大版是縱向編排，都是為了減輕學生記憶口訣的難度。

教材把乘法口訣內容安排在二年級上冊第四單元和第六單元，重構后我們通過一個單元完成“表內乘法”的全部教學。那么，重構后如何整體把握教學目標呢？我們首先羅列關于“表內乘法”兩個單元的教學目標，再以數學課程總目標為準則，根據重構后的單元教學內容和學情進行系統設計及完善。

運用思維導圖“立序”

備學生尤其要注意了解學生的“最近發展區”，找準數學教學的真實起點。以《圓》教學為例，讓學生自學課本，找出生活中的圓，并做一個簡單的思維導圖。

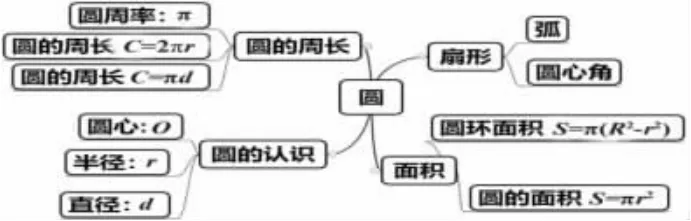
從思維導圖的整理中，學生清晰地梳理出整個《圓》單元的知識內容，并以平行結構羅列了知識點。從思維導圖中分析學生學情，形成課時教學難點、重點。

（3）微課助力設計關鍵問題。

過程探究微課，助力變教為學。在設計微課時要注重前后新舊知識之間的聯系，找準“新”“舊”之間的銜接點，將舊知作為新知學習的“臺階”，充分利用《導學單》，在微課中設置交互式練習，并指導學生展開操作，做到學生自主構建。

案例分享：在教學《平行四邊形面積》的時候，在介紹用轉化法求面積時，從圖形的平移入手，貫穿轉化的本質。

①回顧四年級學過的有關平移的知識，將不規則圖形轉化為長方形。

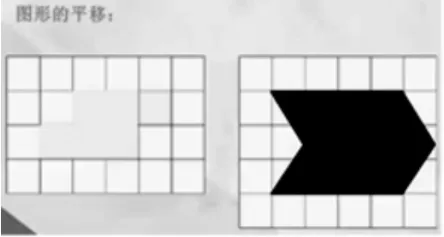
②暫停微課，動手操作，嘗試將平行四邊形通過平移變成長方形。

③展示課前調查的學生操作，并動畫演示。

④思考并操作：除了這種轉化方法，你還有不同的轉化方法嗎？將自己的方法記錄在《導學單》上，帶回到課堂交流。

方法展示微課，助力問題解決。在微課設計中需要充分利用生活中的常識、思維方法，甚至是跨學科的知識,運用技術手段和策略,將重難點的難度弱化，把抽象的數學概念轉變成具體的表象,提高微課學習的實效性。

案例分享：人教版三年級上冊《歸一問題》的微課。微課借助動態演示，把解決問題轉化為畫圖分析歸一問題的變式問題。

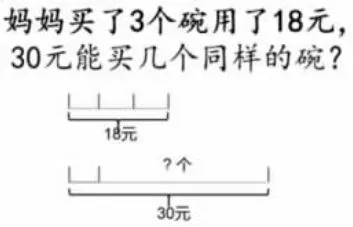
在教學設計中我們從以下四方面突破關鍵問題：

活動一：課前調查，畫圖解決問題。

活動二：補充信息，放手解決問題。

活動三：微課學習，變式練習對比。

活動四：數形結合，模型練習鞏固。

思維拓展導學，提煉思想方法。拓展微課設計是在課堂學習的基礎上，利用數學知識的練習，經過分析、歸納、總結、提升，達到思維的延伸和思想方法的滲透。借助拓展導學微課，學生能夠及時解決練習中的問題，同時更好地提煉和感悟數學思想方法。

案例分享：在《分數乘法簡便計算》教學中，學生已經有整數乘法簡便計算、小數乘法簡便計算的基礎，學習本課知識點不會太難。因此設計了拓展導學微課，簡便計算：，學有余力的學生經過自主解決之后，可以繼續觀看微課，自主學習。首先，觀察數據特點。然后利用數形結合的思想來分析解決。

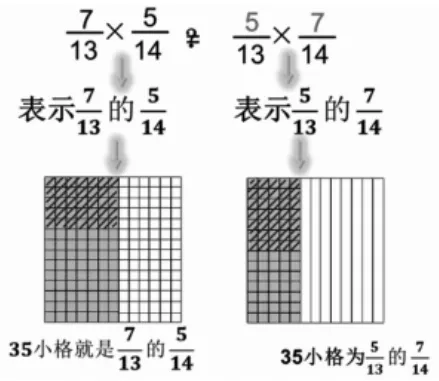
因此，本節課定義關鍵問題：在數形結合下，理解分數乘法簡便計算的意義，這樣學生對于的理解就水到渠成，不僅能夠鞏固分數乘法所表示的意義，同時今后再遇到這樣的簡便計算也能夠快速找到方法，深刻體會數形結合思想的意義，為初中的學習做好鋪墊。