基于FCE-AHP的雙螺桿壓縮機綜合性能研究

宋健忠， 何雪明*， 范海港， 盧立新， 林自東

(1．江南大學 江蘇省食品先進制造裝備技術重點實驗室， 江蘇 無錫 214122；2.山東碧海包裝材料有限公司， 山東 臨沂 276600)

雙螺桿壓縮機因其突出的性能優勢得以在各大工業部門中廣泛使用。而對壓縮機的性能影響最直接的便是雙螺桿壓縮機轉子型線的設計。但針對雙螺桿壓縮機對設計出的轉子型線性能指標仍然未實現統一的計算標準，這將會導致國內外技術交流上產生矛盾和分歧，嚴重阻礙了壓縮機行業技術水平前進的步伐[1-2]。目前，國內外的研究學者一直以單一的轉子型線性能參數：幾何特性參數、熱力學性能以及能效功率等參數作為對壓縮機的整體性能的評判指標，這樣的定性評價往往伴隨著不全面性[3]。為了避免單一的轉子型線性能指標評估引起的片面性和不完全性，雙螺桿壓縮機綜合性能的研究必須要建立一套專門用于其綜合性能的多因素評判體系，以突破當下的困境[4-5]，為中國工業4.0做出一點貢獻。

針對雙螺桿壓縮機的性能評估中難以定量分析的問題，課題組提出了一種基于模糊綜合評判法[6-7]和層次分析法[8]的綜合性能計算方法。

1 模糊綜合評判理論

1.1 模糊綜合評判法的定義

模糊綜合評判法(FCE)一般是指通過模糊變換原理和最大隸屬度原則，就受到多種因素影響的目標作系統全面的考慮，同時對其給予評估分析[9-11]。其基本原理是通過已被確定的被評判對象的評判集和因素集，將模糊評判矩陣和權重矢量[12]加以確定后結合2因素作歸一化處理[13]，借此得到模糊綜合評判的結果。

而對于綜合評判而言，則必須將諸多因素囊括其中，假設選取了n個和被評判對象相關聯的因素，此時記因素集為U,則有：

U={u1,u2,…,un}。

(1)

式中n表示指標因素的數目。

如果對其中任何一個因素的評判根據等級情況進行表征，此時可假設系統對指標因素做了m種不同級別的評判結果，此時其評判集

V={v1,v2,…vm}。

(2)

所以，選擇模糊綜合評判法解決問題時最為關鍵的還是如何建立一個從因素集到評判集的模糊變換法則，建立

R=U×V。

(3)

對U里面的任意因素都做一個重要性判斷，變換詳細過程如圖1所示，得到模糊判斷矩陣

(4)

式中:rij為隸屬度；i=1,2,…，n,表示第i個因素；j=1,2,…,m,表示第j級別評判結果。

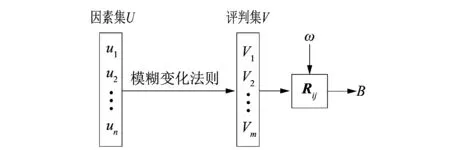
圖1 模糊綜合評判法Figure 1 Fuzzy comprehensive evaluation method

1.2 多級模糊綜合評判法

多級模糊綜合評判較為特殊，是一種基于層次評判的方式，可以較為全面的將被評估的綜合指標加以反映出來，進而從整體來看有效提升了評估的效果。這可以將其應用在雙螺桿壓縮機性能評估中，具體如圖2所示。圖2中列出了雙螺桿綜合性能指標和相關因素的關系情況。

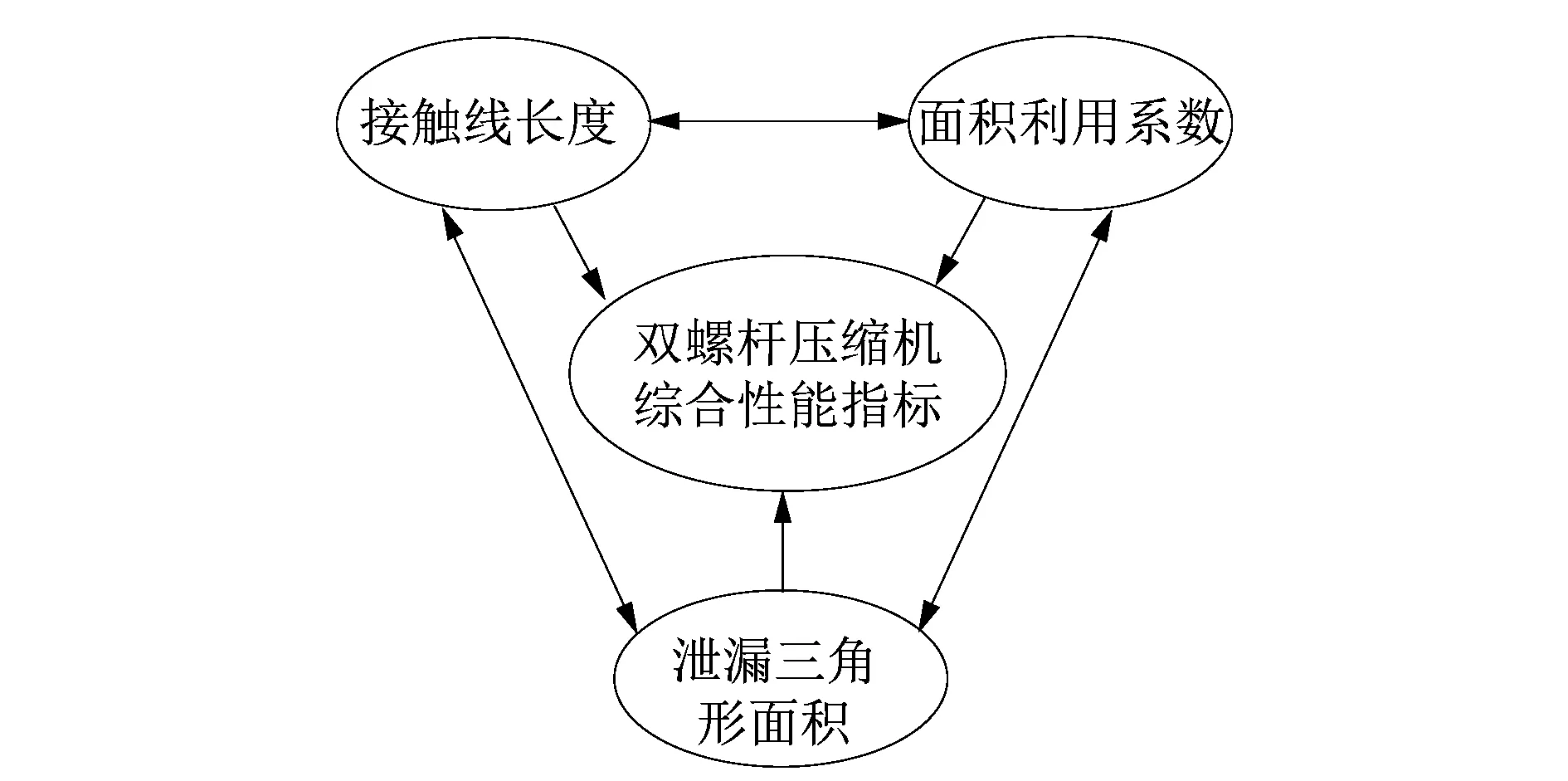
圖2 雙螺桿綜合性能指標多級因素關系示意圖Figure 2 Multi-level factor relationship diagram of comprehensive performance index of twin screw

已知評判集V和因素集U的情況下，根據模糊變換法則計算得到一個相對應的模糊評判矩陣Rij，如果需要將全部因素的綜合影響考慮其中，需要對Rij里面的元素進行求和：

(5)

在所求解的Rij里面一般都選擇通過對每一項Rj進行權重系數的分配，來表征因素集U里面每一個因素對綜合性能指標重要程度的影響。

為體現每個元素重要程度大小，每個因素需要賦予合適的權重系數，得到集合ωi被稱之為權重集。

ωi={ω1,ω2,…,ωn}。

(6)

故模糊綜合評判集可由下式得到：

B=ωi·Rij=[ω1,ω2,…,ωn]·

(7)

式中：B為模糊綜合評判集合，bm為雙螺桿壓縮機轉子綜合性能指標的評判結果。

2 雙螺桿壓縮機綜合性能評估指標體系及權重的擬定

2.1 螺桿壓縮機綜合性能評估指標體系

課題組基于各項參數的研究構建了雙螺桿壓縮機綜合性能評估指標體系如圖3所示，將綜合性能指標和影響因素，以及因素與因素之間的內在聯系直觀的呈現出來。

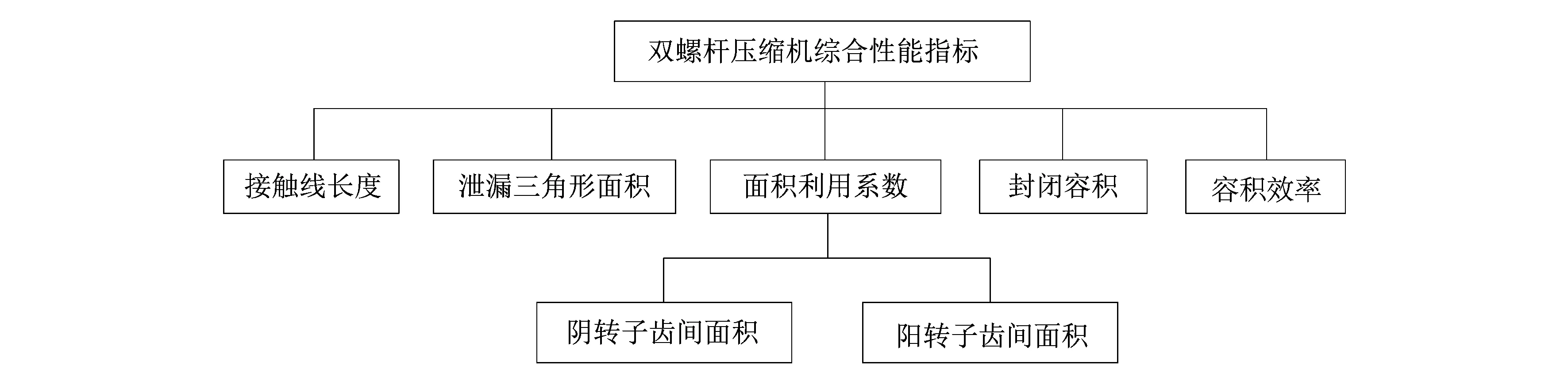
圖3 雙螺桿壓縮機綜合性能評估體系Figure 3 Comprehensive performance evaluation system of twin screw compressor

2.2 評估指標體系的權重

為確保整個評估體系的結果更有說服力，需要對每個因素的權重分配進行充分的考量并賦予合適的權重系數。表1中對常見權重確定方法的優缺點進行了分析。由表1可知層次分析法具有系統性，能夠定性定量分析，計算較為簡單，下面將以層次分析法進行計算。

表1 常見權重確定方法比較

2.2.1 層次分析法的基本原理

層次分析法AHP最早可追溯到美國Saaty教授。為了對各因素占比進行定量分析，盡可能減少主觀意識不確定性的影響，一般可將被測對象劃分為不同的因素，然后以AHP對同一層級因素做兩兩對比，構建判斷矩陣。接下來，通過對應特征向量的歸一化處理和最大特征值的計算可求解得出理想的權重矢量。最后，通過對結果進行一致性檢驗，分析權重分配的合理性[14]。

2.2.2 層次分析法的操作步驟：

1) 評判因素集的確定

評判因素集U={u1,u2,…un}。

2) 判斷矩陣的構造

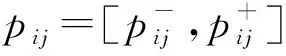
(8)

3) 權重向量的擬定和計算

為了便于計算且文中對精度要求較為寬松，故采用N次方根法求解其特征向量。

①判斷矩陣各行元素之積。

(9)

式中，Mi表示判斷矩陣各行元素之積。

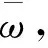
(10)

③為了下一步的一致性檢驗，還需要計算判斷矩陣的最大特征根

(11)

式中向量Pω的第i個元素用Pω,i來表示。

4) 一致性檢驗

由式(10)得到權重系數，但權重的分配是否合理需要進行判斷。所以必須對判斷矩陣進行一致性檢驗，根據已有的檢驗公式(11)可得：

CR=CI/RI。

(12)

式中：CR為矩陣的隨機一致性比率；CI為矩陣的一般一致性指標，其數值可通過公式(11)求得；RI為矩陣的平均隨機一致性指標，具體取值可見表3。

(13)

式中:λmax表示矩陣的最大特征根；n表示因素集中元素的總數。

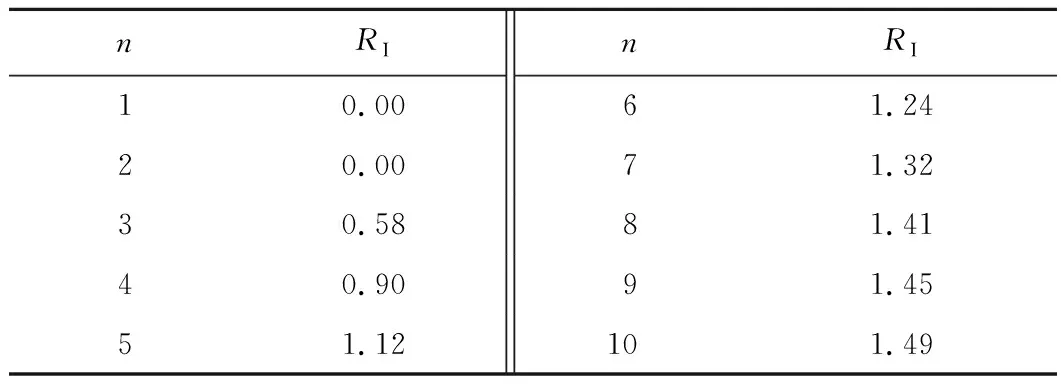
表3 隨機一致性指標RI

若最終求解的判斷矩陣的隨機一致性比率的數值CR<0.1時，那么便認定此矩陣滿足一致性，同時也表明了權重系數的分配是合理的。

3 基于雙螺桿壓縮機綜合性能指標的嚙合線研究

3.1 雙螺桿壓縮機綜合性能評估指標求解

課題組以雙螺桿壓縮機作為研究對象，以模糊綜合層次法進行螺桿壓縮機權重系數與綜合性能指標的求解。而密封性能作為壓縮機最為關鍵的一種指標，其中面積利用系數M、泄露三角形面積S以及接觸線長度L對其影響最為顯著，所以選擇這3種因素用作雙螺桿壓縮機綜合性能的評估。

為便于表達，課題組用K代表綜合性能指標，用L表示接觸線長度，S表示泄露三角形的面積，M表示面積利用系數，建立壓縮機綜合性能評估體系的因素集U={L,S,M}。

1) 構造模糊判斷矩陣

由于判斷矩陣基于互反性1～9標度規則建立而成的。因此根據表2，以各因素的隸屬度為行，可以構成模糊判斷矩陣P=(pij)n×m。雙螺桿壓縮機綜合性能指標隸屬度如表4所示。

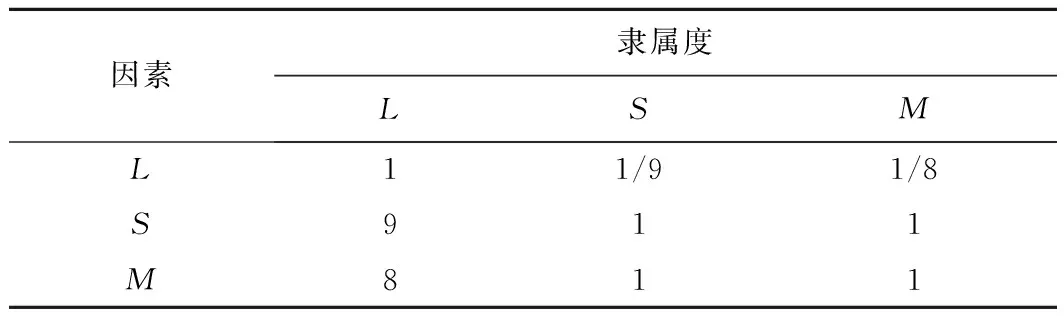
表4 雙螺桿壓縮機綜合性能指標隸屬度

由表4可知模糊判斷矩陣

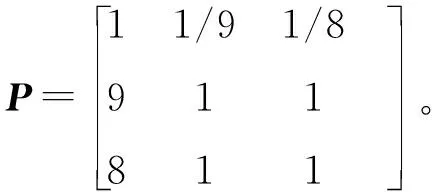
(15)

2) 求解特征向量

課題組在保證精度前提下，采用方根法求解其特征向量。首先計算N次方根

(16)

然后作歸一化處理，其結果為：

(17)

將公式(17)的結果代入公式(11)，得到判斷矩陣的最大特征根

λmax=3.001 5。

(18)

3) 一致性檢驗

已知最大特征根λmax=3.001 5，又m=n=3，根據已有的檢驗式(13)可得到判斷矩陣的一般一致性指標

(19)

根據表3可知，當n=3時，RI=0.58。將CI和RI代入式(12)，得到：

CR=CI/RI=0.000 77/0.58=0.001 3?0.10。

(20)

則符合要求K的關系式可表示成：

(21)

3.2 雙螺桿壓縮機綜合性能分析

課題組用1條6次的NURBS擬合的復盛嚙合線作為原始嚙合線，然后對其進行優化設計，并重點計算每次調整前后的綜合性能指標值[15]。

復盛嚙合線作為一種典型的雙螺桿壓縮機型線，可以依照雙螺桿壓縮機轉子型線計算公式計算得出M，S，L和K的值分別為0.454 2，4.258 8 mm2，148.146 0 mm和1.183 8。

同理，將嚙合線劃分為5個部分：AB，BC，CD，DE和EF。以AB段和DE段最高點H和J和EF段最低點P為界可將AB，DE和EF劃分為左右2段，具體如圖4所示。

圖4 嚙合線分段及對應轉子型線Figure 4 Meshing line segments and corresponding rotor profiles

然后將嚙合線分段并將線段進行調整，分別計算得到如表5所示的接觸線長度L，泄露三角形面積S，面積利用系數M以及綜合性能指標K。

根據表5可知：

1) 當JE段向內調整時：L增大，S不變，M減小，這個結果是不期望看到的，且K=1.188 4>1.183 8。

2) 當JE段向外調整時：L減小，S不變，M增大，這個結果是期望看到的，且K=1.179 5<1.183 8。

3) 當PF向內調整時：L增大，S不變，M減小，這個結果是不期望看到的，且K=1.194 0>1.183 8。

4) 當HB段向內調整時：L增大，S增大，M幾乎不變，這個結果是不期望看到的，且K=1.194 5>1.183 8。

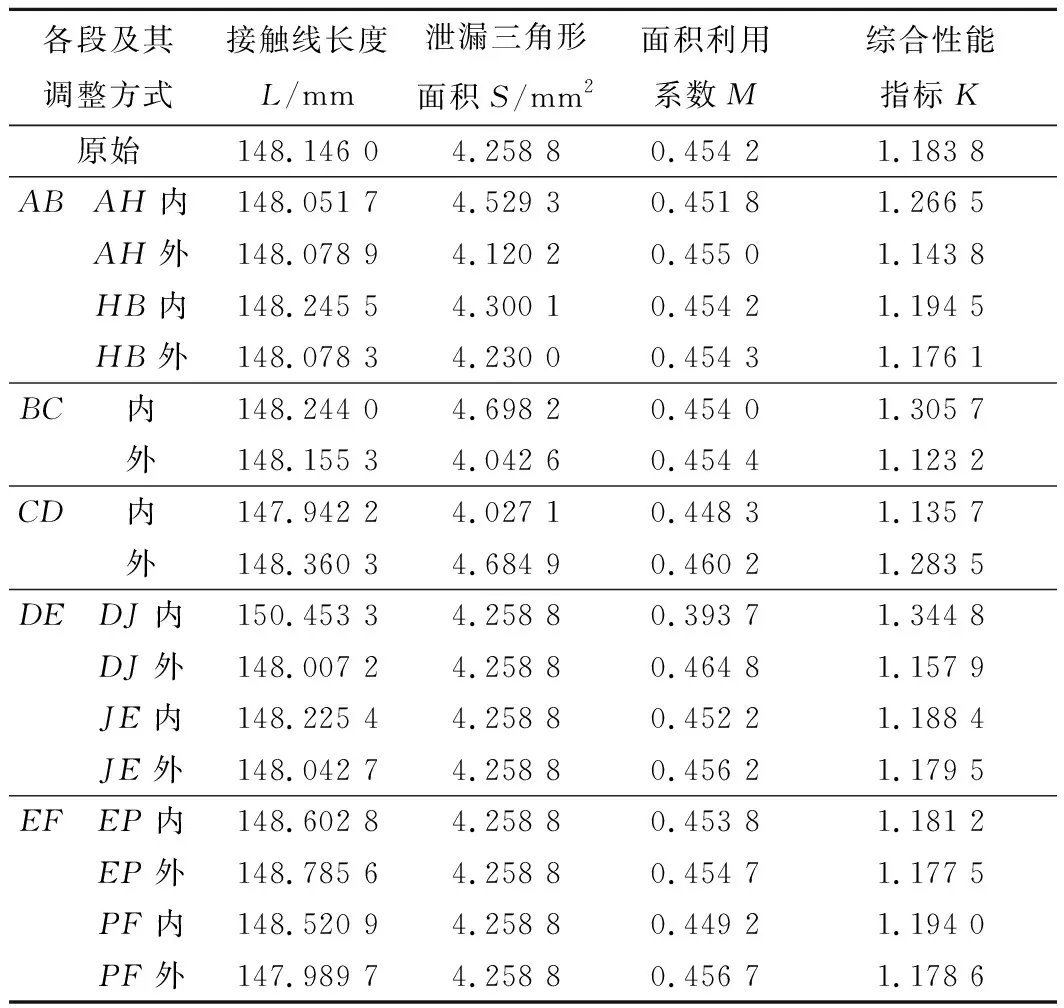
表5 嚙合線各段調整對綜合性能指標的影響

分析表5中數據可知：當嚙合線往性能變好得方向調整時，綜合性能指標K減小；往性能壞的方向調整時，K增大。

能夠使型線性能向更好的方向發展的各段調整方式為：AH向外，HB向外，BC向外，CD向內，DJ向外，JE向外，EP不變，PF向外，詳細調整的方向如圖5所示。

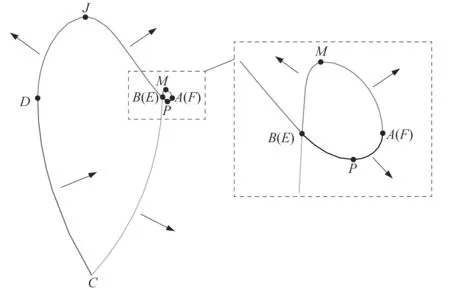
圖5 嚙合線各段優化方向Figure 5 Optimization direction of each section of meshing line

根據圖5的調整方法，將表5中各段的優化調整后的各段型線整合成一條完整的嚙合線，并根據該嚙合線生成一條優化型線，原始型線與優化型線性能參數對比如表6所示。

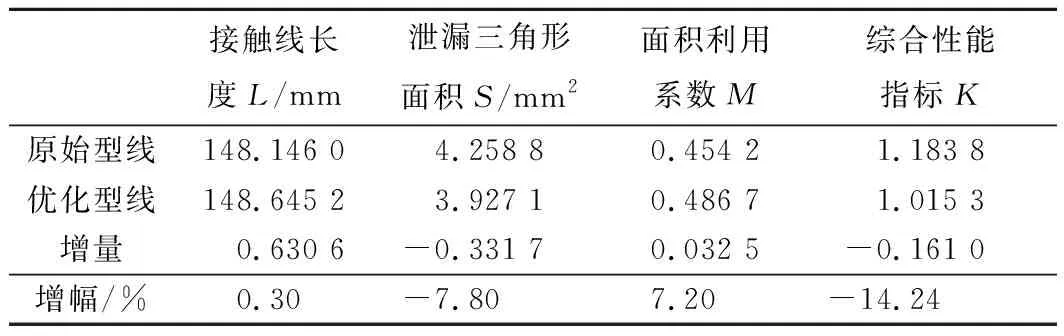
表6 原始型線與優化型線性能參數對比

由表6可知，與原始型線相比，優化型線的接觸線長度略有增加，僅增加0.630 6 mm，相對增加了0.30%；泄露三角形區域面積減小了0.331 7 mm2，相對減小了7.80%；面積利用系數增大了0.032 5，相對增加了7.20%；綜合性能指標相對降低了14.24%，即優化了14.24%，驗證了綜合性能指標表達式作用，能夠有效的表征所設計轉子型線經過優化之后性能指標的改變。

4 結論

針對雙螺桿壓縮機的性能評估中難以定量分析的問題，課題組提出了一種基于模糊綜合評判法和層次分析法(FCE-AHP)的綜合評估解析方法。首先分別對模糊綜合評判法和層次分析法的基本原理以及計算步驟出了詳細的說明；然后建立了雙螺桿壓縮機綜合性能指標的評估體系，并分析了綜合性能指標與各因素之間的關聯性。接下來對比了幾種常用的權重確定方法的優缺點以及適用情況，利用層次分析法分別求解了綜合性能評估指標的權重，并基于多級模糊綜合評判法得到了雙螺桿壓縮機綜合性能指標K的表達式。最后，以1條6次擬合的復盛型線為例，計算其每次調整后的綜合性能指標值，通過分析綜合性能指標K來表征所設計轉子型線優劣變化，證明了所求的綜合性能表達式K可行性，避免了采用幾何特性參數、熱力學性能以及能效功率等方面作為對壓縮機的整體性能的評判指標的片面性與效率低下等問題，對以后轉子型線設計具有借鑒意義。

在后續研究中不僅應考慮最重要的因素，還應增加考慮其他有影響的因素，其中解決運算量較大的問題等尤需繼續探索。