芻議問題導(dǎo)向教學法在初中數(shù)學教學中的應(yīng)用

武放軍，景曉東，卜秀娟

芻議問題導(dǎo)向教學法在初中數(shù)學教學中的應(yīng)用

武放軍，景曉東，卜秀娟

（寧夏銀川市三沙源上游學校，寧夏銀川750001）

問題導(dǎo)向教學法是新課程改革的產(chǎn)物，對于加快初中數(shù)學教學模式轉(zhuǎn)型，提升課堂教學效果具有“四兩撥千斤”之功效，值得教師投入更多時間與精力展開深入探索。筆者現(xiàn)結(jié)合初中數(shù)學教學實際情況，分析問題導(dǎo)向教學法的優(yōu)勢與教學實踐存在的問題，并針對優(yōu)化策略展開探討，以期提升初中數(shù)學教學活動有效性，助力學生數(shù)學核心素養(yǎng)的提升。

初中數(shù)學；問題導(dǎo)向教學法；教學模式

數(shù)學是一門研究數(shù)量、變量、結(jié)構(gòu)等形式科學的學科，由問題構(gòu)筑而成。數(shù)學教學活動是發(fā)現(xiàn)、分析、解決與應(yīng)用各類問題的過程。但是在應(yīng)試教育理念之下，初中數(shù)學過于重視問題的表征結(jié)果，而忽視問題本質(zhì)規(guī)律的探究，導(dǎo)致學生問題意識淡薄、思維定式傾向嚴重、創(chuàng)造能力不足等弊端日益凸顯，課堂教學深陷低效泥潭，師生疲態(tài)盡顯。在此背景之下，以問題為導(dǎo)向的探究式教學方法應(yīng)運而生，受到廣泛關(guān)注，為初中數(shù)學教學轉(zhuǎn)型帶來新的契機。如何充分發(fā)揮問題導(dǎo)向教學法的優(yōu)勢改變教學現(xiàn)狀，成為廣大一線教師需要實踐探索的首要問題。

一、問題導(dǎo)向教學法對于初中數(shù)學教學的意義

相較于傳統(tǒng)講練式教學而言，問題導(dǎo)向教學法更符合初中數(shù)學學科本質(zhì)與素質(zhì)教育理念要求，對于學科發(fā)展與學生成長展現(xiàn)出獨特的優(yōu)勢。第一，有助于提升課堂教學效果。問題導(dǎo)向教學法打破了傳統(tǒng)教學模式下知識自上而下的單項灌輸，而是將數(shù)學知識融入特定問題情境，引導(dǎo)學生通過獨立思考與合作探討，提煉重要知識點。提出問題與解決問題的過程增強了師生之間的有效互動，使學生成為數(shù)學課堂的主人，喚醒主體自覺性，促使學生重新燃起對于數(shù)學學習的欲望，積極主動地參與教學活動。此外，學生對于數(shù)學問題的理解形成了課堂教學的實時反饋，使教師能夠及時掌握學生的思維動態(tài)與學習成果，將以學定教落到實處，提升教學指導(dǎo)的針對性。第二，有助于培養(yǎng)學生的思維能力。問題是實現(xiàn)學生思維可視化的有效途徑，問題導(dǎo)向教學法在初中數(shù)學教學有效運用，能夠促使學生思維時刻保持活躍狀態(tài)。在問題的引導(dǎo)之下，通過聯(lián)想、推斷、分析與論證一系列探究活動剖析數(shù)學知識內(nèi)涵，掌握潛藏在知識表征背后的數(shù)學思想方法，促進數(shù)學思維走向深刻化、靈活化。這樣不僅能夠?qū)崿F(xiàn)對于數(shù)學知識的深層次理解，而且有助于培養(yǎng)學生舉一反三的意識、融會貫通的能力，提升解題能力。

二、問題導(dǎo)向教學法在初中數(shù)學教學中的應(yīng)用現(xiàn)狀

在新課程改革的加持之下，初中數(shù)學教學逐漸向素質(zhì)性、人文性與開放性轉(zhuǎn)變，教師樂于嘗試各類新型教學模式，為問題導(dǎo)向教學法的順利實施提供了有利條件。但是在現(xiàn)行中考機制之下，新舊理念處于膠著狀態(tài)，問題導(dǎo)向教學法的應(yīng)用情況并不樂觀。

（一）問題設(shè)置存在局限性

雖然教師對于問題的育人價值達成了普遍共識，但是在課堂教學活動中的問題設(shè)置卻差強人意。具體而言，存在以下方面的問題。第一，重視問題數(shù)量而忽視質(zhì)量。初中數(shù)學的問題導(dǎo)學法應(yīng)以學生的認知需求為出發(fā)點，以培養(yǎng)學生的數(shù)學思維能力為落腳點，問題應(yīng)做到精準有效，但是在實際教學過程中卻存在本末倒置的情況。一些教師存在為了提問而提問的情況，對于學生數(shù)學思維推進需求考慮不足，導(dǎo)致課堂設(shè)問過于頻繁。過于密集的一問一答，看似是在帶動學生思維，實則大多為無效問題，并未對學生認知層次與思維能力起到促進作用。此外，一些教師并未對提問目的與提問對象進行精準分析，隨機性的提問方式導(dǎo)致真正需要鍛煉的學生未能獲得回答機會。同時，對于學生而言，過難或是過于簡單的問題反而起到反作用效果，影響學生的思維活躍性。第二，問題類別過于單一。目前一些教師設(shè)計的教學問題單純地指向解析計算，帶有濃厚的嚴肅、刻板色彩，使本就對數(shù)學存在畏難情緒的學生徒增心理壓力，一定程度上削弱了學生深入探究問題的欲望。此外，初中數(shù)學課堂的問題設(shè)計缺乏啟發(fā)性與開放性，大多指向基本概念、基本知識以及基本解題方法，其教學功能更加傾向于知識的傳輸載體，而并非學生思維的延展支點。固化的問題設(shè)計使學生盲目地追求結(jié)果的準確性，對于問題中蘊含的知識規(guī)律以及數(shù)學思想方法的探究不夠深入，影響學生的進一步探索。

（二）問題分析存在淺薄性

對于問題導(dǎo)向教學法而言，分析與解決問題的過程是整個教學模式的核心，一定程度上決定了課堂教學的廣度與深度。但是就目前而言，問題分析環(huán)節(jié)的設(shè)計與實施差強人意，對于問題的分析過于淺顯，教與學并未形成相互作用的良性互動。第一，從教師角度而言，未能充分發(fā)揮主導(dǎo)作用。教師不僅是問題的提出者，更是帶領(lǐng)學生解決問題的引導(dǎo)者，需要認真觀察學生的課堂反應(yīng)，分析表征行為下的認知阻礙，但是在初中數(shù)學實際教學過程中，其實踐并非如此。教師把握不住誘導(dǎo)時機的情況普遍存在，導(dǎo)致為學生提供的幫助指導(dǎo)存在“過”與“不及”的問題，不論何種情況都對于學生自主分析與解決問題能力的發(fā)展產(chǎn)生不利影響。此外，問題自主解析時間設(shè)置較短，預(yù)留給學生的回答時間較匱乏，導(dǎo)致學生尚未理清解題思路，教師已然宣布正確答案。此種快節(jié)奏的問答方式偏離了問題導(dǎo)向教學法的初衷，淪為形式主義。第二，從學生角度而言，初中階段學生正值獨立意識形成的過渡時期，呈現(xiàn)自主性與依賴性并存的認知特點，面對強調(diào)學生自主能力的問題導(dǎo)學法展現(xiàn)出或多或少的不適應(yīng)。一方面學生過于依賴教師的引導(dǎo)，在問題分析環(huán)節(jié)，一些學生遇到復(fù)雜的問題展現(xiàn)出思維惰性，單純地等待教師的講解，而并未嘗試獨立解決。另一方面學生過于依賴自身固有經(jīng)驗，遇到新問題習慣于搜索曾經(jīng)遇到過的類似題目或是采用常用的思維方式，極易形成思維定式，影響問題的分析深度。

（三）問題運用存在滯后性

在素質(zhì)教育視域之下，初中數(shù)學旨在培養(yǎng)學生運用數(shù)學知識與數(shù)學思維解決實際問題的能力。問題導(dǎo)學法的運用同樣需要立足于學生實際應(yīng)用能力的發(fā)展，但是教師采用的引導(dǎo)方式不盡合理，導(dǎo)致問題喪失了其應(yīng)有的育人價值。具體而言，第一，課堂的問題指導(dǎo)過于單一。在問題導(dǎo)學實踐過程中，教師大多采用傳統(tǒng)的師生問答方式，某位學生說出準確答案，問題互動即為結(jié)束，對學生的思維過程缺乏指導(dǎo)。對于一些疑難問題，雖然教師組織學生展開互動交流，但是對于學生的探討結(jié)果關(guān)注度不夠全面，忽視了學生認知與思維碰撞產(chǎn)生的課堂生成性資源。不僅削弱了學生的探究成就感，打擊學生主動思考與勇于質(zhì)疑的積極性，而且扼殺了初中數(shù)學教學的多元化發(fā)展，不利于學生的個性思維的形成。第二，課后的問題反思不夠深入。問題導(dǎo)學法并非僅僅停留于課堂時間，課后問題拓展是促進學生內(nèi)化吸收與認知升華的關(guān)鍵。但是實際上，課后的反思與歸納、應(yīng)用與實踐卻極易被忽視。由于缺失了自主建構(gòu)環(huán)節(jié)，學生對于課堂知識的理解停留于淺嘗輒止的層面，不僅影響數(shù)學知識的長時記憶，而且導(dǎo)致學生欠缺靈活運用的能力，削弱了問題導(dǎo)向教學方式的教學效果，影響初中課堂的學習深度。

綜上所述，問題導(dǎo)向教學法的應(yīng)用存在諸多局限性，其教學價值未能得到充分釋放，圍繞關(guān)鍵問題調(diào)整課堂活動的組織策略是突破教學瓶頸，構(gòu)建高效課堂的重要舉措。

三、問題導(dǎo)向教學法在初中數(shù)學教學中的應(yīng)用策略

（一）設(shè)計多樣問題，激發(fā)探究欲望

問題導(dǎo)向教學法能否順利實施的關(guān)鍵在于核心問題的設(shè)置。因此，教師應(yīng)以激發(fā)學生的探究欲望為切入點，以滿足不同認知程度學生的學習需求為落腳點，嚴謹?shù)睾Y選課堂問題，構(gòu)建螺旋遞進式問題階梯，引領(lǐng)學生數(shù)學思維的層層深入。以“線段、射線、直線”教學為例，首先，在教學導(dǎo)入環(huán)節(jié)，教師采用趣味性游戲達到激趣引學的目的。如借助多媒體教學設(shè)備展示琴弦、手電筒光束、鐵軌、蜿蜒的公路等生活場景，構(gòu)建問題情境：“你能夠從中找到哪些熟知的平面圖形？”立足學生“最近發(fā)展區(qū)”設(shè)計思考問題，將數(shù)學知識與生活事物建立緊密聯(lián)系，幫助學生實現(xiàn)由具象到抽象的認知轉(zhuǎn)變，促使學生快速進入思考狀態(tài)。其次，在新知識的探索環(huán)節(jié)，教師設(shè)置具有導(dǎo)向性與啟發(fā)性的問題，帶領(lǐng)學生抽絲剝繭，理清數(shù)學知識本質(zhì)。如“你能說出線段、射線與直線的特點嗎？該怎樣表示呢？”引導(dǎo)學生有目的地自主閱讀教材內(nèi)容，提煉關(guān)鍵知識信息。又如“你知道三者存在怎樣的區(qū)別與聯(lián)系嗎？”引導(dǎo)學生通過動手操作與對比分析深化數(shù)學概念。在完成理解基礎(chǔ)理論知識的基礎(chǔ)上，教師設(shè)置開放性問題，提升思維能力。如，讓兩名同學相互握手，一共握手幾次？那么三名同學呢？n名同學又該怎樣表示呢？引導(dǎo)學生跳脫表象，分析數(shù)學知識的內(nèi)在規(guī)律。通過具有明確目標指向的層層遞進式的問題鏈條設(shè)計，讓學生時刻保持思維的活躍性，引領(lǐng)學生走向深度學習。

（二）合作分析問題，鍛煉思維能力

在大力倡導(dǎo)互助、合作、探究教學模式的當下，為學生創(chuàng)造自主學習空間，激發(fā)同伴合作與互動交流，是有效落實問題導(dǎo)向教學法的重中之重。因此，教師堅持先學后教的原則，采取多元化的問題交流方式，以學生合作探討結(jié)果作為教學指導(dǎo)的起點，提升初中數(shù)學課堂教學活動的靈活性，鍛煉學生的思維能力。

（三）巧妙解決問題，滲透思想方法

對于問題導(dǎo)向教學法而言，解決問題僅僅是淺層認知的表現(xiàn)，深入分析問題中蘊含的數(shù)學思想與高效的解決方法是教學的本質(zhì)。基于此，教師應(yīng)轉(zhuǎn)變盲目重視結(jié)果的問題引導(dǎo)方式，強化學生思考與分析問題的過程，引導(dǎo)學生學會透過現(xiàn)象看本質(zhì)，促進數(shù)學知識的內(nèi)在轉(zhuǎn)化。以《二元一次方程與一次函數(shù)》教學為例，此章節(jié)內(nèi)容是滲透數(shù)形結(jié)合思想的重要載體，教師引導(dǎo)學生自主探索解決問題的方法，分析方程與圖像之間的關(guān)系，了解數(shù)學知識的結(jié)構(gòu)性與關(guān)聯(lián)性，促進數(shù)形結(jié)合意識與能力的初步形成。首先，教師借助問題實現(xiàn)溫故而知新，如舉例說明什么是二元一次方程、什么是二元一次方程的解、二元一次方程有幾個解、怎樣畫出函數(shù)圖像等等。教師通過引申學生的固有知識與經(jīng)驗，實現(xiàn)知識的梳理與整合，促使學生由模糊的概念或符號認知向數(shù)學規(guī)律轉(zhuǎn)變。在此基礎(chǔ)上，教師提出預(yù)測性問題：二元一次方程的解與相對應(yīng)一次函數(shù)圖形存在怎樣的關(guān)聯(lián)性？教師以固有知識作為起點，提出新的疑問，引出教學探究主題，帶領(lǐng)學生分析數(shù)學知識的關(guān)聯(lián)性，完成對于固有知識的深化與重組。其次，教師以教材例題著手，在關(guān)鍵的思維節(jié)點提出問題，如方程組的解與函數(shù)圖像的交點坐標存在什么關(guān)系？引導(dǎo)學生對二元一次方程與一次函數(shù)進行對比分析。

（四）深度探究問題，形成知識結(jié)構(gòu)

問題導(dǎo)向教學法的精髓在于如何激活學生數(shù)學思維，引導(dǎo)學生理清問題本質(zhì)，學會多維度地辯證性思考數(shù)學問題，嘗試運用多種方法解決問題，在問題的加持之下對于數(shù)學知識本質(zhì)內(nèi)涵形成更深層次的理解，建立結(jié)構(gòu)化的認知體系。基于此，問題導(dǎo)學并不單純的是提問與回答，而應(yīng)注重學生思考問題的方式與視角，教學活動應(yīng)具有開放性與啟發(fā)性。以《有理數(shù)的乘法》教學為例，有理數(shù)作為初中數(shù)學的學習基礎(chǔ)，此知識模塊是學生開展后續(xù)數(shù)學知識深入學習的必要條件，其教學重難點在于有理數(shù)乘法法則的理解。針對初中學生思維能力的局限性，教師可以將問題進行分解，形成指向性的思考活動。首先，教師引導(dǎo)復(fù)習，引出新知。如給出-2+（-2）；-2+（-2）+（-2）；-2+（-2）+（-2）+（-2），讓學生觀察，復(fù)習熟知的知識點。給出（-5）×3；（-5）×4，幾組算式，讓學生合理地猜想運算數(shù)值。在此基礎(chǔ)上，針對兩個有理數(shù)相乘有幾種情況展開探討，學生對于含有負數(shù)數(shù)值的乘法心存疑惑，教師故意留下懸念，激發(fā)學生的求知欲望。其次，教師構(gòu)建問題情境，如處于0點的蝸牛以每分鐘2cm的速度向0點左右爬行，思考不同時間節(jié)點蝸牛的方向。通過引入圖文結(jié)合的解析方式，引導(dǎo)學生探索正數(shù)與負數(shù)。在問題情境的支持之下，從具體算式中總結(jié)出運算規(guī)律。通過啟發(fā)性的問題引導(dǎo)學生經(jīng)歷數(shù)學知識的完整推導(dǎo)過程，加深知識理解與掌握。

（五）綜合運用問題，學會舉一反三

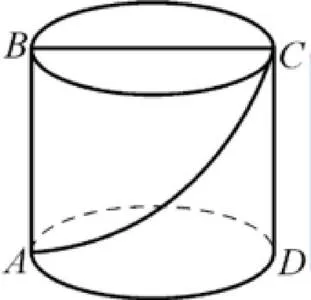
借助問題導(dǎo)學法培養(yǎng)學生的分析能力與運用能力，能夠創(chuàng)造性地運用數(shù)學知識解決數(shù)學問題是教學的關(guān)鍵。因此，教師注重問題的實踐應(yīng)用，促使學生做到舉一反三，從個性的問題中分解共性規(guī)律，推動數(shù)學思維由典型向一般化拓展。以《勾股定理》教學為例，教師以經(jīng)典的螞蟻爬行最短路線問題為切入點，處于A點的螞蟻，應(yīng)該怎樣以最短的距離爬行至C處吃到美味的食物（如圖所示）。引導(dǎo)學生展開合作探究，規(guī)劃不同的路線進行對比分析，探尋最優(yōu)解，在分析問題答案的過程中加深對勾股定理的理解。在此基礎(chǔ)上，進一步深化思考層次，提出歸納類思考問題，該題目中蘊含了怎樣的數(shù)學思想方法，組織學生梳理思考步驟，明確如何審題、建立數(shù)學模型、怎樣求解以及檢驗其合理性。以此促使學生的關(guān)注點不再拘泥于解決問題本身，而是根據(jù)實際問題構(gòu)建數(shù)學模型形成代表自我意志的獨特思維方式。教師根據(jù)學生的理解情況，出示幾組相同類型的變式問題，考查學生理解情況的同時加快客觀知識與學生主體的融合。讓學生以此打破思維定式的束縛，能夠思辨性地審視數(shù)學問題，根據(jù)題目做到舉一反三，提升實際應(yīng)用能力。

四、結(jié)語

總而言之，在素質(zhì)教育視域之下，初中數(shù)學強調(diào)以人為本、學以致用，以培養(yǎng)學生認知水平與靈活運用能力為目標。問題導(dǎo)向教學法是落實“學貴有疑”教學精神的直觀體驗，對于平衡師生主體關(guān)系，落實素質(zhì)教育要求提供了有力加持。但是不可否認，在當前教學形勢之下，問題導(dǎo)向教學法在初中數(shù)學教學的有效運用仍然面臨諸多挑戰(zhàn)。這就需要教師緊跟時代發(fā)展步伐，把握新課改的命脈，挖掘問題導(dǎo)向教學法的育人價值，不斷創(chuàng)新課堂組織形式，促進學生數(shù)學綜合能力的發(fā)展。

[1] 王力爭,劉歷紅.基于中學課堂變革的結(jié)構(gòu)化教學實踐探索[J].當代教育與文化,2018,10(06):42-50.

G633.6

A

1002-7661(2022)16-0060-03