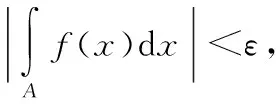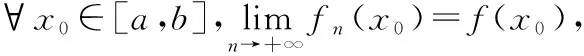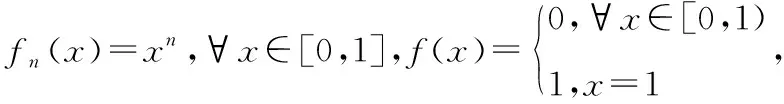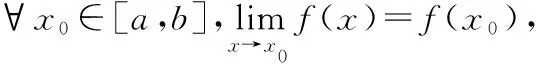“定義比較法”在實變函數課程教學中的運用
李小朋 (河北工業大學 理學院,天津 300401)
在數學學習的各個階段,我們會遇到各種各樣的定義,而不同場合下的數學定義,有些名字很像甚至完全一樣,這并不是巧合,它們之間一定有著很深刻的聯系,我們要學會發現它們之間的聯系,這對我們學習數學定義有著很大的幫助,在實變函數中就有很多這樣的例子,以下是兩個實例.
一、集合序列上下極限和數列上下極限之間的比較
實變函數理論是集合論體系之下的,所以幾乎每本實變函數教材的開始都會介紹基本的集合論知識,其中一個重要概念就是集合序列的上下極限.我們先看看集合序列上下極限是如何定義的:
定義1(集合序列上下極限):對于一串給定的集合A1,A2,…,An,…,我們稱
{x:有無窮多個n,使得x屬于An}
{x:只有有限多個n,使得x不屬于An}
很多同學都感覺這個概念太抽象,難以理解,而數學分析里正好也有一個相似的定義,就是數列的上下極限.在聯系這兩個定義之前,我們需要把數學分析中一些相關定義進行拓展,這是因為在數學分析體系,并沒有引入有關無窮大的計算,而在實變函數中需要引入無窮大的相關計算.
首先是上下確界的概念需要進行拓展.數學分析中的確界存在公理說的是有上界的數集必有上確界,有下界的數集必有下確界,上下確界的定義局限于只能描述有界集合,這里我們可以把上下確界的定義拓展到無界集合,一個無上界集合的上確界定義為+∞,一個無下界集合的下確界定義為-∞.其次是單調收斂定理也可以拓展,原來單調收斂定理是單調有界數列必有極限,現在可以拓展為:任意單調數列都有極限,單調增加數列的極限就是這個數列轉化為數集的上確界,單調減小數列的極限就是這個數列轉化為數集的下確界.這樣數列上下極限的討論范圍就可以從數學分析中的有界數列變為一般數列.
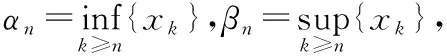
則αn↑,βn↓.由于單調數列一定有極限,所以
分別稱為數列{xn}n≥1的下極限和上極限.
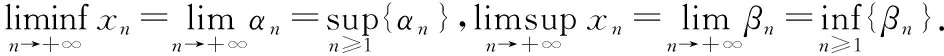
首先最容易直觀感受集合序列極限變化過程的就是單調集合序列,雖然對于集合來說缺少了上下確界這個定義的輔助,但我們同樣可以對集合實現上下確界的內涵邏輯,數集的下確界的直觀解釋是最大下界,對于集合序列來說其最大下界恰好可以用交運算來實現,一列集合的交集正好比每一個集合都“小”,而且是最“大”的那個比每個集合都“小”的集合.相應的,數集的上確界的直觀解釋是最小上界,對于集合序列來說其最小上界恰好可以用并運算來實現,一列集合的并集正好比每一個集合都“大”,而且是最“小”的那個比每個集合都“大”的集合,這樣我們就可以定義單調集合序列的極限了.
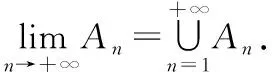
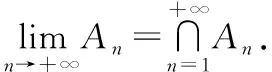
這樣最簡單的集合序列情形我們就刻畫好了.
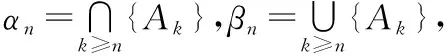
定義2(集合序列上下極限):設{An}n≥1是一個集合序列,
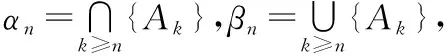
由于單調集合序列一定有極限,所以
分別稱為集合序列{An}n≥1的下極限和上極限.
這個版本的集合上下極限定義和原始定義在形式上有所區別,但本質上是等價的,下面我們來證明定義“1”和定義2這兩個版本的集合序列上下極限的定義等價:
定理:對于一串給定的集合A1,A2,…,An,…,都有下面兩式成立:
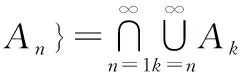
證明:
先證明第一個等式:對任意x屬于左邊集合,則有無窮個N,使得X屬于An,因此對任意大于等于1的自然數N,N之后一定有自然數K大于等于N,使得X屬于Ak,如若不然,就和已知有無窮多個An包含X矛盾,即X屬于右邊的集合,所以左邊的集合包含于右面的集合;另一方面,對任意X屬于右邊集合,由交集和并集的定義,對任意大于等于1的自然數N,都存在大于等于N的自然數K,使得X屬于Ak,按此邏輯,對于N=1,應存在n1,使得X屬于An1,對于N等于n1+1,應存在n2大于n1,使得X屬于An2,依次類推,我們可得到數列n1 再來證明第二個等式:對任意X屬于左邊的集合,則至多有有限個An不包含X,假設一共有I個An不包含X,按下標從小到大順序記為An1,An2,…,Ani,這樣當K大于ni時,一定有X屬于Ak,即X屬于等式右邊的集合,所以等式左邊的集合包含于等式右邊的集合;另一方面,對任意X屬于等式右邊的集合,由交集和并集的定義可知,存在N使得,對任意N大于等于N,必有X屬于An,這說明只有當N小于N時才可能有X不屬于An,即至多有有限個An不包含X,所以等式右邊的集合也包含于等式左邊的集合,綜上,等式兩邊集合相等. 相信通過上面定義的比較,同學們通過定義2更容易理解和記憶集合序列上下極限這個相對比較抽象的數學定義. 實變函數中的EGOROFF定理給出了函數列幾乎處處收斂如何轉化為一致收斂的方法,其中函數列一致收斂和函數一致連續以及勒貝格積分下的函數族一致可積這三個定義中都提到了“一致”,它們之間有沒有什么聯系呢?雖然前兩個定義在數學分析的學習中就已經學過了,可大多數同學對這兩個定義理解得都不到位,再加上更難理解的函數族一致可積這個新定義,更是不知所云.其實通過定義的比較,找出三者內在的邏輯聯系,這對理解這三個定義非常有幫助.我們先看看這三個定義的具體描述. 定義3(函數列一致收斂) 設函數列{fn(x)}n≥1和函數f(x)定義在閉區間[a,b]上,如果對?ε>0,都?N≥1,使得對?x∈[a,b],當n≥N時,有|fn(x)-f(x)|<ε, 則稱函數列{fn(x)}n≥1在[a,b]上一致收斂于f(x). 定義4(函數一致連續) 設函數f(x)定義在閉區間[a,b]上,如果對?ε>0,都?δ>0,使得對?x∈[a,b],?y∈[a,b],當|x-y|<δ時,有|f(x)-f(y)|<ε,則稱函數f(x)在閉區間[a,b]上一致連續. 這三個定義看上去有些相似,但又有很大差別,但事實上,當我們選對觀察角度時,三者的思維邏輯是完全一樣的.所有收斂都會涉及三個問題:第一是收不收斂?第二是收斂到誰?第三是收斂的速度是多少?我們現在研究的這三個定義中關鍵詞“一致”,主要是和第三個問題相關,當我們站在收斂速度這個角度來觀察,就會發現三者之間的聯系. 其次,我們再來看函數一致連續這個定義,我們只需要把定義中的符號稍微換一下,我們馬上就能發現兩者的聯系. 定義4*(一致連續)設函數f(x)定義在閉區間[a,b]上,如果對?ε>0,都?δ>0,使得對?x0∈[a,b],?y∈[a,b],當|x-y|<δ,有|f(x0)-f(y)|<ε,則稱函數f(x)在閉區間[a,b]上一致連續. 最后,我們來看函數族一致可積這個定義,函數族一致可積的另一個叫法是積分等度絕對連續函數族,來源于可積函數的絕對連續性,這里所說的“連續”和函數的連續在形式上有區別,但本質邏輯是一樣的,它是指當積分區域A的測度趨于0時,f(x)的絕對值在A上的積分也相應地趨于0,這里我們可以把連續函數的概念抽象成一個連續映射φ來理解,把自變量對應積分區域A的測度值,而把f(x)的絕對值在A上的積分運算值對應映射本身,因為當積分區域測度為0時,積分值一定是0,所以我們刻畫的這個映射φ在自變量為0時,對應的映射值也是0,即“φ(0)=0”,當F為可積函數時,由可積函數的絕對連續性定理,當自變量(也就是A的測度值)趨于0時,映射φ的像趨于φ(0)=0,這和普通函數在0點的連續性是一樣的,因此才有“連續”這個叫法.再回到定義5,對任意f∈F可看出當mA趨于0時,有f(x)的絕對值在A上的積分趨于0,但是不對不同的F,積分值趨于0的速度是不一樣的,這個速度正是由定義中的ε和δ的配比關系所決定的,相同ε時,可取得的δ越大,收斂速度越快,反之則越慢,而定義5中的ε和δ是可以控制每一個F的收斂速度,也就是找到了一個所謂的“最慢收斂速度”,這就和前面兩個定義中“一致”完全對應上了,事實上數學里有很多和“一致”相關的定義,基本上都是這個邏輯,所謂一致,一定是和無窮個收斂速度相關,在這無窮個收斂速度里如果能找到一個最慢的收斂速度,也就是前面反復提到的那個“控制速度”,那就是“一致”的,相信經過這樣的比較,學生會對這三個定義有了更加深刻的認識.二、函數列一致收斂,函數一致連續以及函數族一致可積之間的比較