基于改進粒子水平集法的近壁面液滴下落過程數值模擬

陳鐵軍，房 媛，田 輝*

(1.河北省承德市興隆縣政府辦公室,河北 承德 067300；2.河北石油職業技術大學 機械工程系,河北 承德 067000)

液滴下落過程普遍存在于多相流系統、噴墨打印、涂裝工藝及降雨過程等領域，在此過程中的運動、變形甚至破碎現象一直深受學者的關注。Eggers[1]基于系統的理論分析獲得了液滴下落變形及破碎的非線性動力學規律。Stone[2]著重分析了表面張力影響下低雷諾數時下落液滴的變形規律。其研究顯示：低雷諾數時液滴下落過程滿足連續性方程及斯托克斯方程，液滴變形的程度主要受兩相間表面張力作用影響。Leal[3]發現液滴的尾跡受慣性力影響顯著表現出非線性特點。

由于下落過程中液滴與周圍空氣間存在懸殊的密度、粘性差異，使得相界面變形等遷移特性的數值研究困難重重，國內外專家學者相繼提出了一系列求解算法，如MAC[4]方法、Front Tracking[5]法、VOF[6]法、Level Set[7]法等。然而以上單一算法中仍存在系統質量守恒性差、捕捉界面不夠準確(稅利的界面細節被算法抹平)等問題。CLSVOF[8]、Particle Level Set[9]等混合方法的提出有效的改善了以上問題。本文在經典粒子水平集法(Particle Level Set)的基礎上通過改進距離函數修正方式實現高精度兩項界面遷移過程的捕捉并保證系統質量守恒性，為解決液滴下落等復雜工程問題提供有效途徑。

1 無量綱控制方程組

本文通過一套無量綱不可壓縮流體控制方程組[10]求解氣液兩相流動(如方程組1-4所示)，不考慮氣液兩相間質量傳遞；氣液兩相相應區域以不同的物性參數表征，無質量虛擬粒子隨流場遷移模擬相界面的遷移運動。計算中均使用無量綱參數，則描述變密度不可壓縮流動問題的無量綱控制方程組可描述為張量形式：

(1)

(2)

(3)

(4)

2 改進粒子水平集法

粒子水平集法將拉格朗日思想及歐拉思想良好的結合在一起，為多相流相界面遷移運動問題的準確求解提供了有力的工具。然而算法中粒子對距離函數的修正策略局限于網格內部，當待修正網格點、逃逸粒子及界面不在同一網格內的時候，現有方法所獲得的修正值存在一定偏差[11]。

本文不再采用根據網格點距離函數的正/負來對局部距離函數的求解進行分類。這里借助如圖1所示的虛線l來判定待修正網格點局部距離函數的求解方式。虛線l過投影點P′且其斜率由此處界面切向量決定。l將計算域分為兩部分，若待修正點與原始水平集法確定的界面位于同一側，則局部距離函數可通過方程(5)獲得；若待修正點與原始水平集法確定的界面分別在虛線l的兩側，則局部距離函數通過方程(6)獲得。

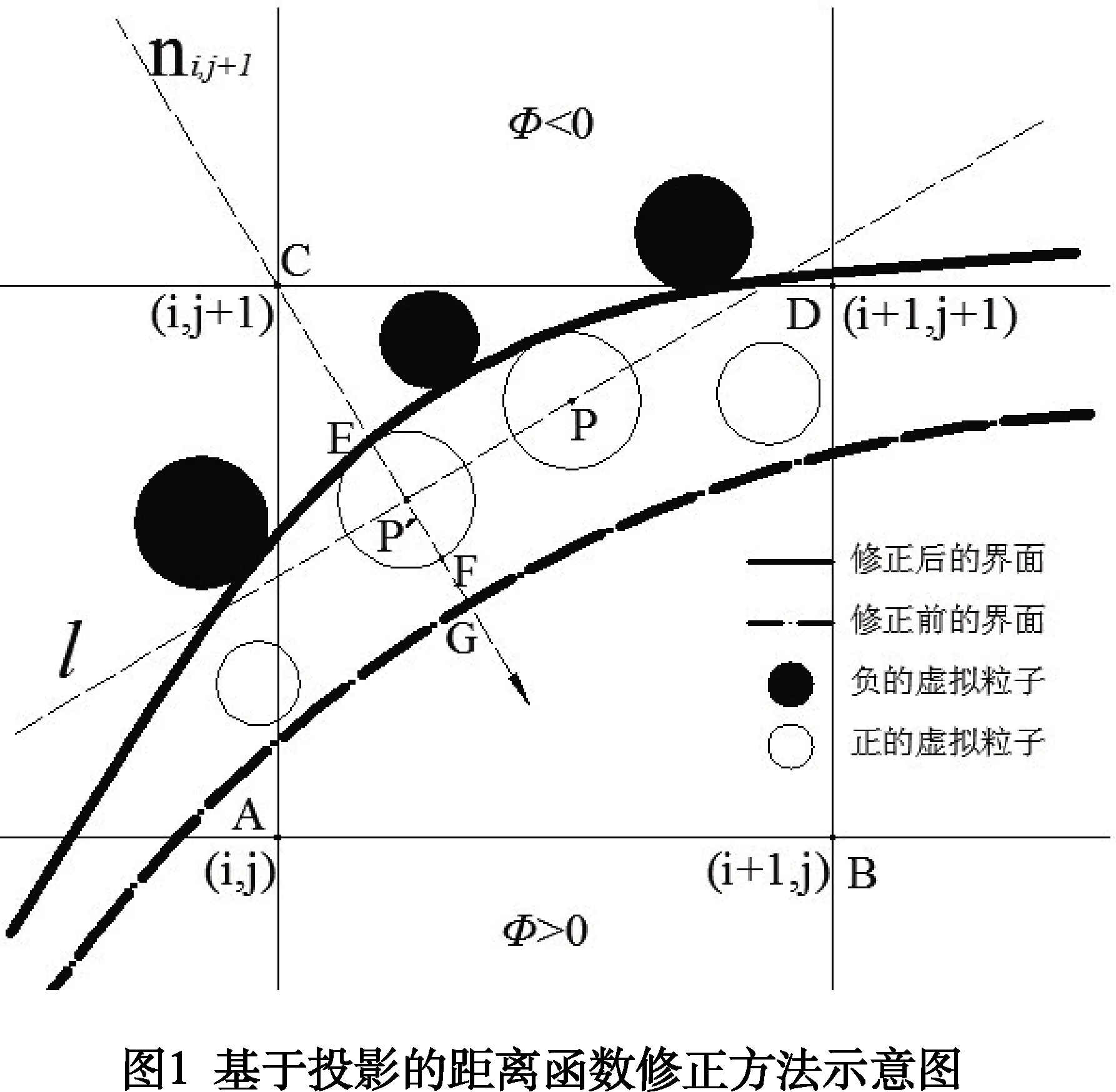
φP(x)=Sp(rp+|x-xp′|)

(5)

φP(x)=Sp(rp-|x-xp′|)

(6)

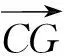
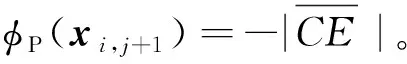
(7)

3 控制方程離散求解方式

4 液滴下落過程的數值模擬

液滴在重力作用下的下落及浮力作用氣泡的上升過程受以下控制參數影響：兩相的密度ρ液和ρ氣，兩相的動力粘性系數μ液和μ氣，重力加速度g，兩相間表面張力系數σ，空間位置xi以及時間T。基于π定理，通常選取以上8個變量所構成的5個獨立變量來描述此問題[14]。本文采用的控制參數為：(1)密度比ρ液/ρ氣；(2)動力粘性系數比μ液/μ氣；(3)無量綱時間T；(4)Re數(Reynold number)；(5)Eo數(Eotvos number)。

(8)

(9)

(10)

液滴下落過程的數值模擬在1×2的矩形計算域中進行，采用結構化均分網格，計算域四邊均為壁面無滑移邊界條件，CFL數設為0.1。液體密度設為ρ液=1 000 kg·m-3，動力粘性系數設為μ液=1.137×10-3Pa·s保持與水一致，初始全場速度均為0。

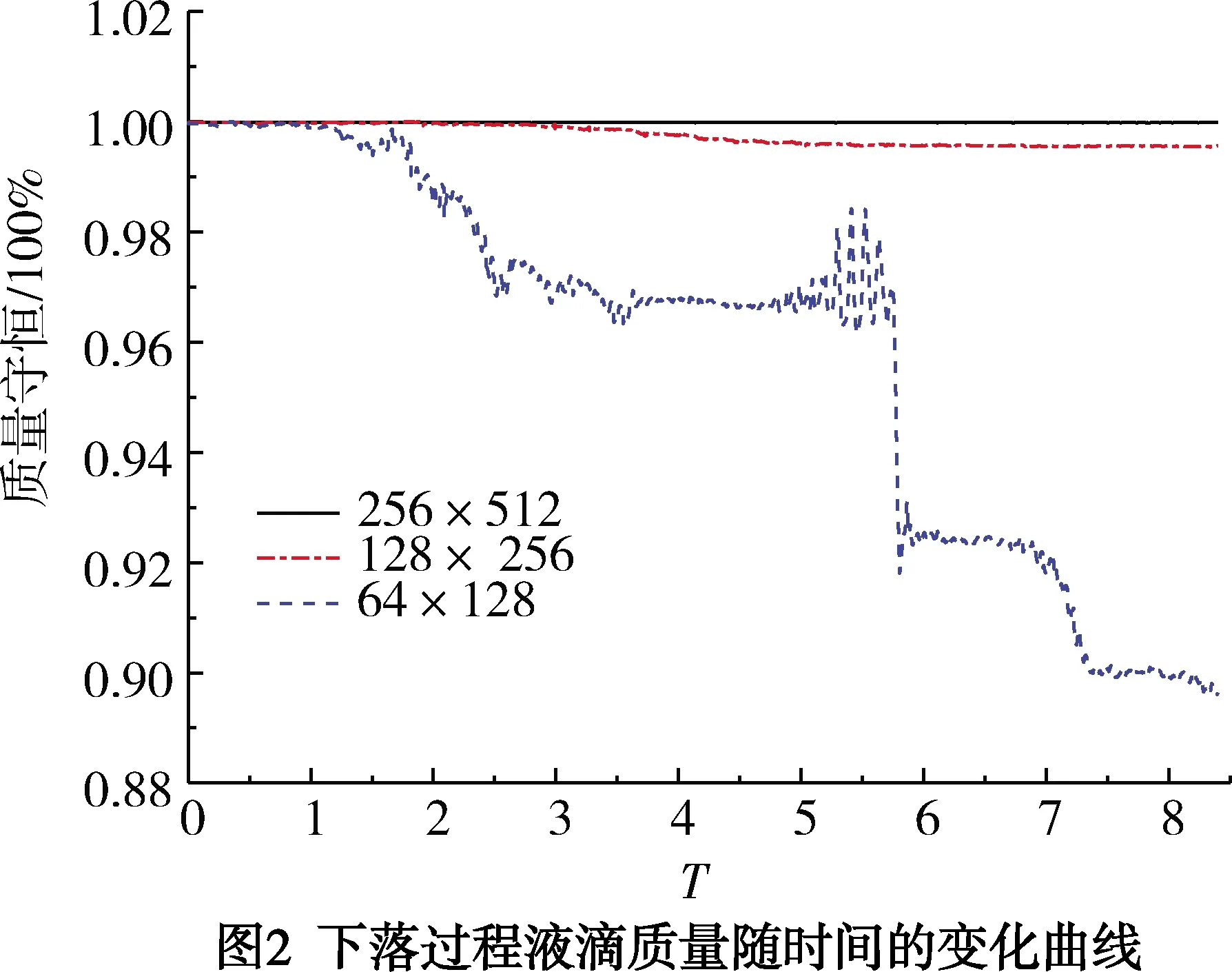
首先對后續數值模擬采用的網格進行無關性驗證。分別采用三種結構化網格：64×128、128×256、256×512，液滴直徑為D，初始于(0.5,1.7)，Re=200，We=100。圖2給出了三種情況下液滴質量(面積)守恒特性。采用64×128網格時液滴的質量虧損嚴重，液滴發生破裂后質量虧損超過10%，計算過程CPU耗時325 s；采用128×256網格時液滴的質量虧損較小，液滴發生破裂前后質量虧損始終保持在1%以內，圖3給出了三種網格下液滴下落過程典型形態。圖中可見三種情況液滴變形情況極其相似，且網格數的增加使液滴表面更光順。圖3(a)中可見液滴邊緣粗糙的棱角。計算過程CPU耗時4 167 s；采用256×512網格時液滴的質量虧損幾乎可以忽略，但消耗大量計算資源，CPU耗時129 527 s。兼顧求解精度及計算效率，本文均采用128×256的網格對液滴的相關流動過程進行數值研究。

在壁面無滑移邊界條件的影響下，近壁面的流動區域存在明顯的速度梯度，流動表現為剪切流。如圖2所示，液滴破碎后在近壁面區域受壁面作用，下落過程出現明顯的左右擺動現象。本文通過數值模擬到壁面不同距離液滴的下落過程，分析總結壁面作用對下落液滴運動、變形的影響。

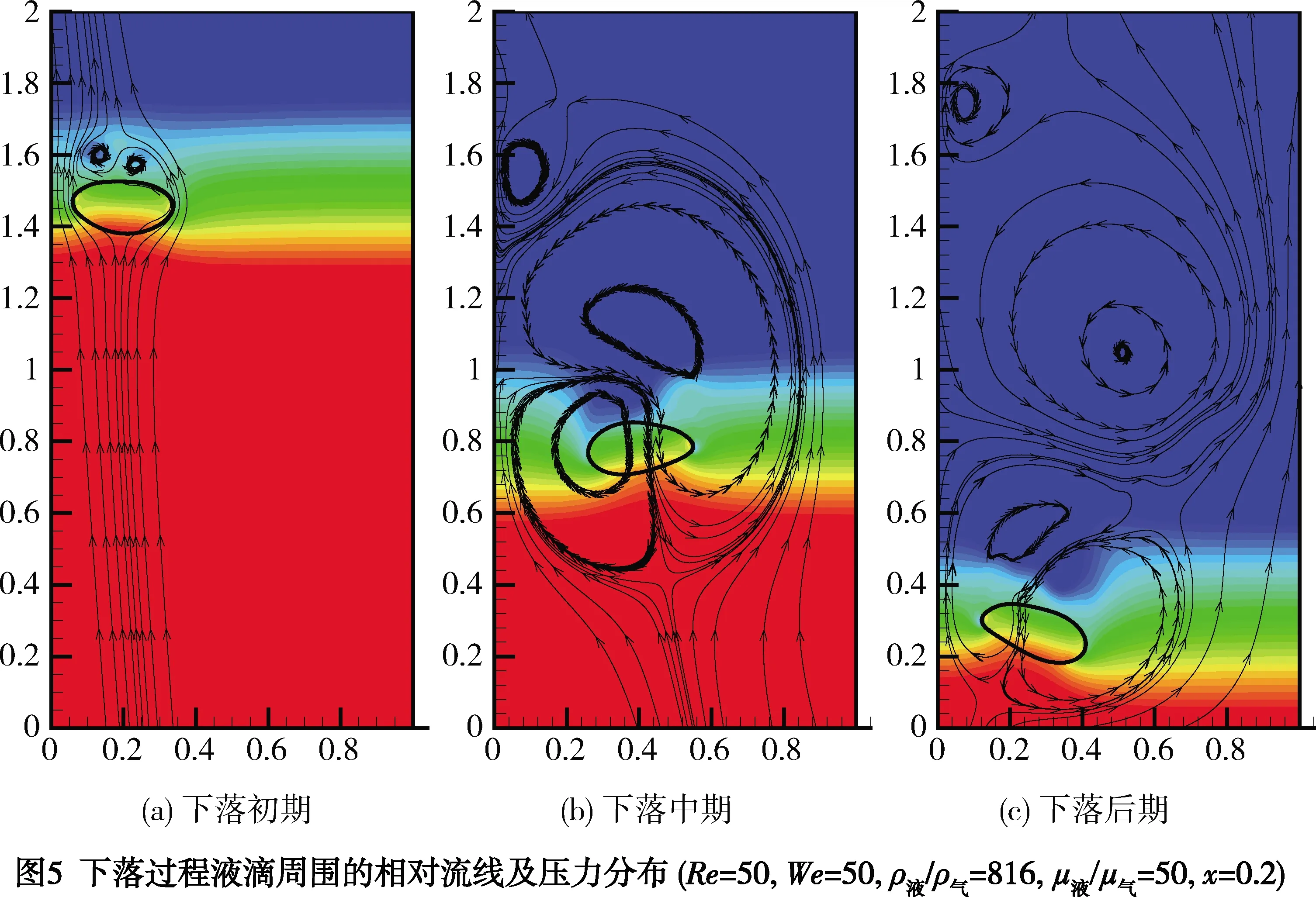
圖4為到壁面不同距離的三個液滴下落過程，到壁面距離分別為D、1.5D、2D。圖中可見壁面對液滴下落過程影響顯著，越靠近壁面此作用越突出。三種情況液滴下落初期均首先向靠近壁面一側擺動，但很快便開始向另一側擺動，到一定極限時擺動方向調轉，如此反復直至下落到底。以圖4(a)的情況為例，液滴初始時刻圓心到壁面的距離為D，圖5給出了此過程中三個典型時期液滴變形、相對流線及周圍壓力的分布(紅色表示高壓區域，藍色表示低壓區域)。計算域內絕對速度場減去液滴的平均速度可得到液滴的相對速度場，相對流線便是在此相對速度場中繪出的。液滴下落初期水平及垂直速度均較小，液滴左右兩側變形差異很小整體呈現為橢圓形，相對流線緊貼液滴下側，而上側出現兩個強度較小且旋向相反的兩個渦，液滴左右兩側壓力基本一致。隨著液滴的下落流場趨于復雜，液滴下落中期相對速度場中出現了三個影響范圍較大的渦。液滴呈現出類似雞蛋的形狀且大頭在左側，其周圍流場完全被旋向相反的兩個渦控制。此時液滴頂部左右兩側壓力不平衡，左側略低。液滴下落后期情況與下落中期恰好相反，雞蛋形的液滴大頭在右側，液滴頂部右側壓力略低，另外相對速度場中出現了四個渦。

5 結論

本文在推導求解氣液兩相流無量綱控制方程組的基礎上，針對傳統粒子水平集法距離函數修改方式缺陷，提出了一種基于逃逸粒子投影法判斷待修正點與界面位置進而完善距離函數修正的方法。在此基礎上針對壁面作用下液滴在空氣環境中的下落過程進行了數值模擬，數值計算結果顯示：下落液滴在近壁面剪切流影響下發生擺動，而液滴的左右擺動誘發其尾跡區內產生渦；另外強度及影響范圍不斷增加的渦又會影響液滴的后續運動；渦產生后其強度及影響范圍不斷發生變化然而渦的中心穩定于液滴晃動方向發生調轉的區域。本文所發展的數值求解方法具有較高的界面捕捉精度，適用于求解存在高密度差、高粘性差、互不相容的多相流界面遷移運動。