關于薄利多銷問題的建模分析

韋碧鵬，黎會蘭，蒙 仁

（1.柳州職業技術學院，廣西 柳州 545006；2.北部灣大學，廣西 欽州 535011）

0 引言

為了增加商品的銷量，通過降低商品的價格來增加利潤的方式簡稱為“薄利多銷”。在現實生活中，很多商家都是通過這種策略來擴大銷售的。根據彈性分析理念，如果商品價格下降，那么富有彈性商品的需求量將會增加，其增加的幅度將會大于商品價格下降的幅度，從而使得所產生的利潤增加，“薄利多銷”的方式在實際生產經營活動中已經被廣泛應用。本文以2019年全國大學生數學建模競賽E題為例，對“薄利多銷”所產生的問題進行分析和研究。

問題一：問題中給出了商場2016年11月30日到2019年1月2日（以下簡稱“促銷時間”）的銷售流水數據，計算其每天的營業額和利潤率（注意：由于復雜因素的影響，所得到非打折商品成本價的數據是不完備的，一般情況下，零售商的利潤率為20%～40%)。

問題二：根據對題目的理解，建立合適的指標和商場打折力度的數學模型，并對商場促銷時間每天的打折力度進行計算。

問題三：運用題目所給數據，分析打折力度與銷售額、利潤率之間的關系。

問題四：在問題三的基礎上，根據商品的大類進行區分，分析打折力度與銷售額、利潤率之間的關系。

1 問題一模型的建立與求解

1.1 原始數據的預處理

問題一要計算出商場每天的營業額和利潤率，首先要建立數據匹配的數學模型，運用SQL Server2014軟件[1]把促銷時間的商品銷售流水記錄表進行整合，得到銷售流水記錄原始表，共1221855條數據。通過觀察銷售流水記錄表，發現銷售流水記錄原始表不屬于完備的數據，存在著不完備的數據現象。一方面，銷售記錄原始表中存在著顧客未完成的訂單數據（96664條數據），這些數據對于問題的處理沒有任何意義，因此，需要對未完成訂單數據進行剔除。另一方面，銷售流水記錄原始表中存在著大量的商品成本價格缺失，缺失數據占總數據的64.1%。舍棄這些數據對結果的準確性將造成較大影響。經過對問題和數據進行研究，本研究將對成本缺失數據進行修復，其中數據缺失情況分為以下三種：單件商品銷售記錄中從未出現過成本價；單件商品銷售記錄中出現過成本價，但仍存在成本價缺失；單件商品銷售記錄中沒有成本價缺失。

針對以上三種情況，研究使用SQL Server2014軟件將從未出現過成本價的數據、出現過成本價但仍存在成本價缺失、沒有成本價缺失的數據分別取出，得到從未出現成本價表、出現成本價表、未缺失成本價表，接著對從未出現成本價表、出現成本價表進行以下處理[2-3]。

對出現過成本價的商品以成本價為目標，對數據進行去重，得到商品出現過成本價的信息，再根據成本價信息求出利潤率的均值，以利潤率均值為標準，計算并填充相同商品中成本為空的數據。

對從未出現過成本價的數據，將以相同的門店價利潤率為指標，對未出現過成本價的數據進行成本價計算并填充；對存在的有效打折商品，按促銷開始時間和結束時間為條件，商品編號為表示與銷售記錄表中的數據進行匹配，發現還存在有113條數據成本價為空，即可用折扣信息表在促銷時間內對應的商品成本價填充，且將門店價、銷售價及成本價之間不合理的數據進行剔除（如成本價〉門店價）。

1.2 商場營業額和利潤率的模型與求解

使用SQL Server2014軟件將處理后的從未出現成本價表、出現成本價表以及未缺失成本價表進行整合，最終得到完整銷售記錄表，總共1125132條數據，接著為計算出商場每天的營業額和利潤率建立營業額和利潤率相應的數學模型，分別如下。

營業額數學模型：

利潤率數學模型：

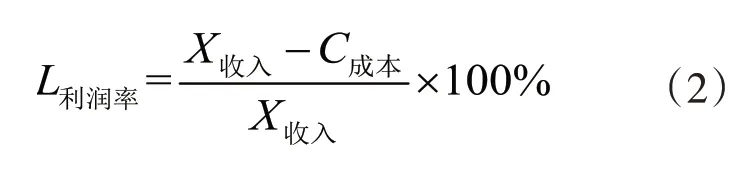
根據模型（1）和模型（2），運用SQL Server2014軟件進行計算，得到每日營業額表和每日利潤率表，見表1所示。

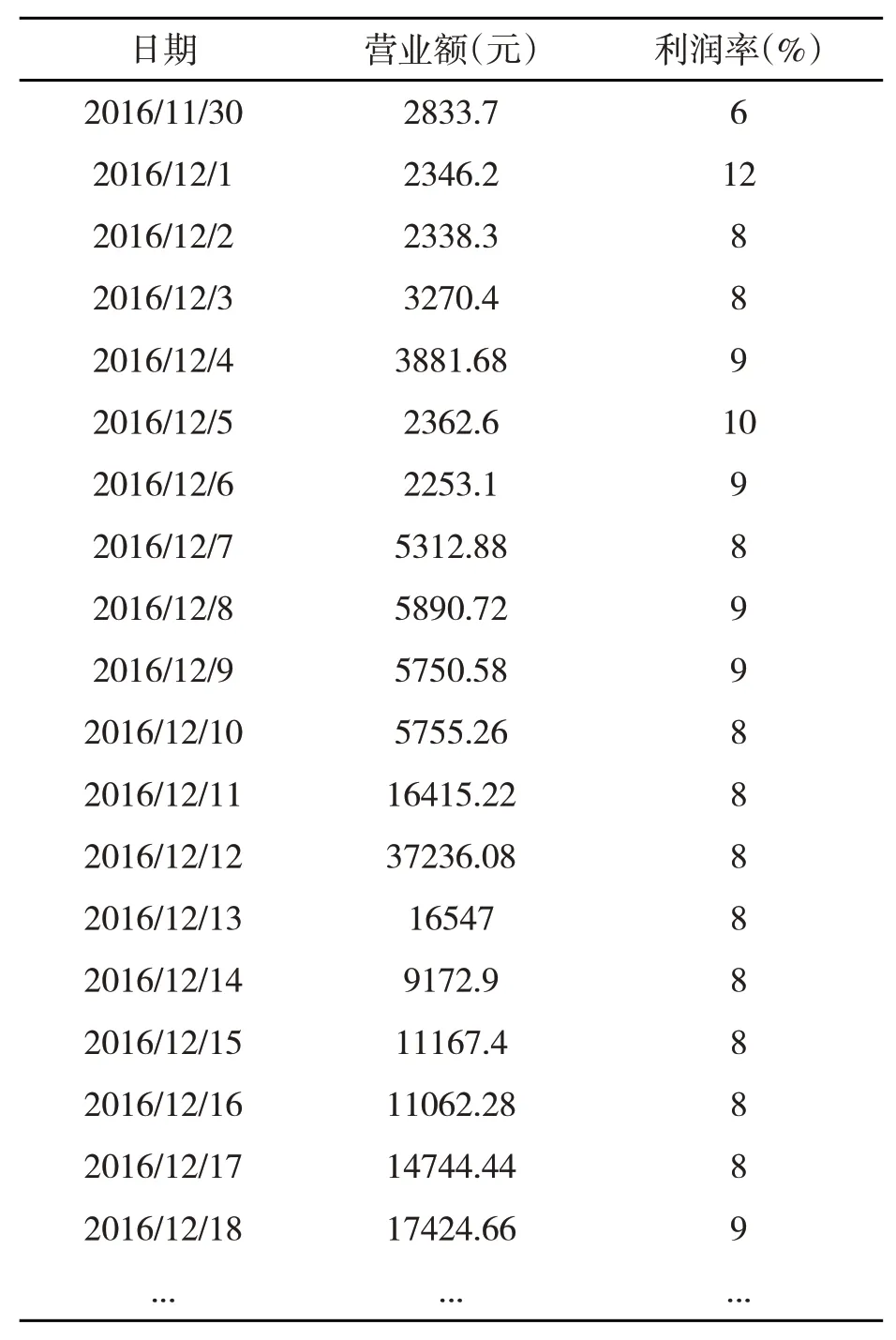
表1 商品每日營業額表和每日利潤率表

2 問題二模型的建立與求解

針對問題二，要計算商場促銷時間每天的打折力度[4-5]，首先需要建立單件商品打折力度的數學模型，具體如下。

單件商品打折力度數學模型：

由于商場每天銷售的商品種類繁多，因此，要計算出商場每天的打折力度，有以下幾種方法：第一，計算出總的商品銷售額和總的商品門面價格，運用模型（3）進行求解，從而得出每天商場的折扣率；第二，運用模型（3）把每天商場銷售每種商品的折扣率都計算出來，然后對其求平均值；第三，考慮商品的屬性不一樣和顧客的偏向問題，采用線性加權的方法，建立多個商品打折力度的數學模型，接著運用問題一原始數據預處理所得到的完整銷售記錄表，從而得出每天商品的打折力度。

以上第一、第二種方法沒有考慮到商品的屬性不一樣和顧客的偏向問題，因此，采用線性加權的方法，建立多個商品打折力度的數學模型，具體如下。

其中T打折力度表示每天商場的打折力度，Mi表示第i種商品的門面價格，Xi表示第i種商品的銷售價格，Wi表示第i種商品的顧客偏好（即權重）。

結合模型（3），可以把模型（4）變為：

為計算出每天的打折力度，根據顧客的偏好，本研究以顧客購買第i種商品的數量與當天商品銷售總數量之比作為第i種商品的權重值，基于此，模型（5）可改進如下：

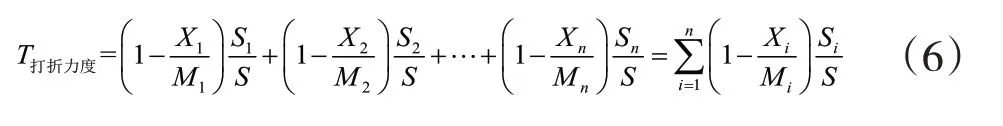
其中，Si表示第i種商品的銷售數量，S表示當天商品銷售的總數量。

運用問題一原始數據預處理所得到的完整銷售記錄表，結合模型（6），可以得出商場促銷時間每天的打折力度，具體如表2所示。

表2 每天商場的打折力度

3 問題三模型的建立與求解

針對問題三，分析打折力度與其他兩個因素銷售額與利潤率的關系，以便從數據中挖掘出其隱含的信息。按照每天商品和單件商品兩個角度進行分析，對打折力度、銷售額以及利潤率之間的關系進行相關性分析和線性回歸擬合，最后運用隨機數據和神經網絡模型驗證所得模型的正確性。

3.1 每天商品角度分析

通過運用SQL serve2014軟件計算并篩選每天打折力度、每天商品銷售額、每天利潤率的數據，得到每天打折信息表（736條數據）。將每天打折信息表導入SPSS軟件，使用皮爾遜相關系數[6]進行分析，得到如下結果。

皮爾遜相關系數：

表3 每天商品打折力度、銷售額以及利潤率的相關性

從表3可知，每天商品的打折力度與商品利潤率的皮爾遜相關性值為-0.685，它們具有負相關性，每天商品的打折力度與商品銷售額的皮爾遜相關性值為0.431，它們存在著一定的關聯。通過觀察每天商品的打折力度、商品利潤率以及商品銷售額的顯著性關系，發現它們之間存在著非常顯著的關系。基于此，本研究運用回歸分析法建立相應的回歸分析模型[7]，具體如下。

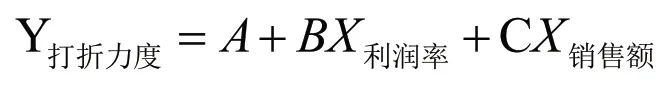
將每天打折信息表導入SPSS軟件中，運用回歸分析中的逐步回歸分析法對數據進行擬合，得到每天商品的打折力度、商品利潤率以及商品銷售額的關系模型：

為檢驗模型的正確性，隨機抽取50條樣本數據對模型（7）進行檢驗，結果如圖1所示。

圖1 模型（7）預測值與真實值數據對比

通過圖1檢驗結果可知，研究建立的模型（7）通過了檢驗，即模型（7）能夠表示每天商品的打折力度、商品利潤率以及商品銷售額的關系。

為進一步檢驗模型的正確性，研究運用神經網絡模型對每天商品信息作進一步分析，使用python3.7編程語言調用tensorflow2.0建立神經網絡模型，將每天打折信息表導入后，以銷售額、利潤率作為自變量，打折力度作為因變量，建立多元線性回歸模型。初始化兩個權重：model.add(layers.Dense(1,input_dim=2))，接著使用adam優化算法與均方差編譯模型：model.compile(optimizer='adam',loss='mse')，將模型配置好后即可對模型進行數據訓練。將每天打折信息表代入模型訓練（model.fit(x,y,epochs=1000)），訓練次數為1000。訓練結束后發現模型的損失函數沒有得到飽和的趨勢，但是，已經被降到了很低的值，隨機代入一條數據進行檢測。

圖2 神經網絡模型對隨機一條數據檢測結果

由上圖中可知，預測的打折力度為0.09276434，對模型作進一步檢測，隨機取10條數據，得出以下情況。

表4 神經網絡模型對商品打折力度的預測值

從上表中，得到模型的預測值和真實值較為接近，即從另外的角度驗證了模型（7）的正確性。

3.2 單件商品角度分析

與上述方法相同，運用SQL serve2014軟件將每件商品的打折力度、商品銷售額以及商品利潤率的數據求出，將數據導入SPSS軟件中，對單件商品的打折力度、商品銷售額以及商品利潤率進行相關性分析，得到如下結果。

圖3 單件商品打折力度、銷售額以及利潤率的相關性

從圖3可知，單件商品的打折力度與單件商品利潤率的皮爾遜值為-0.328，它們的關系呈負相關。單件商品的打折力度與單件商品銷售額的皮爾遜值為0.016，其顯著性大于0.01，顯著性不強，基于此，研究對數據進行矩陣散點圖分析，得到如下結果。

圖4 單件商品打折力度、銷售額以及利潤率的矩陣散點圖

首先，運用SQL Server2014軟件對完整銷售記錄表的商品信息表以類目的形式進行匹配，從而得到各類目下的銷售記錄表。接著，從一級類目、二級類目和三級類目的角度分別對打折力度與銷售額、利潤率進行相關性分析，建立對應的關系模型。

研究先對數據進行處理，使用SQL Server2014軟件求出每件商品的利潤率、打折力度、銷售額，得到每件商品打折信息表（共7325條數據）。接著，將商品打折信息表和商品的信息類目進行數據匹配，發現一些數據與商品的信息類目表數據無法匹配，即商品打折信息表中的一些商品信息查詢不到。為得到完整的數據表，將舍去這些數據，最終得到以類目進行分類的數據（共6570條數據）。

從一級類目的角度分析商品打折力度、商品銷售額以及商品利潤率的關系，將一級商品類目數據表導入SPSS軟件中，使用SPSS軟件的相關性分析功能，對商品打折力度、商品銷售額以及商品利潤率進行分析，發現它們之間的相關關系不強。運用回歸模型檢驗，發現它們之間的顯著性指標過高，因此，得不到一個好的線性規劃模型。

從二級類目的角度對其作相關性分析，發現商品打折力度與商品利潤率的皮爾遜值為-0.519，具有負相關性。然而，商品打折力度與商品銷售額沒有相關關系，因此，運用SPSS對二級類目下的數據進行線性回歸擬合，得到二級類目下的線性回歸模型：

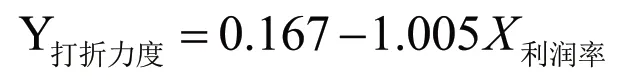
從三級類目的角度分析，與二級類目的角度分析結論類似。發現商品打折力度與商品利潤率的皮爾遜值為-0.313，具有負相關性。然而，商品打折力度與商品銷售額沒有相關關系，因此，運用SPSS對三級類目下的數據進行線性回歸擬合，得到三級類目下的線性回歸模型：

從矩陣散點圖可以看出，單件商品打折力度、銷售額以及利潤率的關系都沒有呈現出明顯的線性關系。

4 問題四模型的建立與求解

在問題三的基礎上，根據商品的大類進行區分，分析打折力度與銷售額、利潤率之間的關系。

將二級類目下的模型、三級類目下的模型以及模型7進行對比，發現商品類目下線性回歸模型的銷售額顯著性普遍偏高。隨機抽取50條數據，將三個模型代入進行驗證，將結果進行線性圖繪制。

從上圖中可知，二級類目下的模型與原模型的折線圖幅度波動較為接近，二級類目和三級類目間的數據十分接近，因此，得出每天的商品打折力度對二級類目下商品的打折力度影響不大的結論。

5 模型的分析、推廣及改進

5.1 模型分析

薄利多銷模型的建立，有助于全國大學生數學建模競賽工作的開展，對參賽學校和學生提高競賽水平具有一定的參考意義，為學生掌握大數據分析技術奠定了必要的基礎。薄利多銷模型的建立和分析，操作性強，便于實現，在大數據時代應用價值高，對傳統實體店的運營具有一定的指導意義。

5.2 模型推廣

該模型以大學生數學建模競賽為背景，問題為實際問題，根據商場的銷售流水記錄、折扣信息表以及商品信息表，分別建立了薄利多銷的銷售額、利潤率以及打折力度的數學模型，分析它們之間的關系。模型可推廣到各大商場和電商平臺中，例如大潤發實體店、天貓、淘寶、京東等。

5.3 模型改進

第一，在問題三中，檢驗所建立的模型正確性時，隨機運用少量的數據對模型進行檢驗，雖然得到的結果比較好，但是，建議運用大量的數據對模型進行檢驗效果更好；第二，分析商品打折力度、商品銷售額以及商品利潤率之間的關系，如果能從時間的角度進一步分析不同時段商品打折力度、商品銷售額以及商品利潤率的關系，其所得結果和應用價值將會更好。

6 結語

薄利多銷是商家擴大銷售的一種策略。為了研究薄利多銷的數學模型，本文結合2019年全國大學生數學建模競賽E題進行研究，詳細地對商場薄利多銷的銷售流水記錄進行分析和建模，分別得到了營業額和利潤率、商品打折力度、銷售額及利潤率的數學模型，且通過數據比較和神經網絡方法驗證提出模型的正確性和有效性，從而為商家促銷提供數據依據。